第六章 平託圖 (Pintographs)

原作：Keith Peters https://www.bit-101.com/blog/2022/11/coding-curves/

譯者：池中物王二狗(sheldon)

blog: http://cnblogs.com/willian/

原始碼：github: https://github.com/willian12345/coding-curves

曲線藝術程式設計系列第 6 章

另一個可用於模擬繪製複雜曲線的物理裝置叫平託圖(Pintograph), 事實上我真的自己弄了一個。

我們將從一個視訊開始--這個第一個按 Pintograph 字面意思在 Youtube 找上找到的視訊

https://www.youtube.com/embed/1JyNLzdbcz4?feature=oembed

平託圖也可以認為是諧波圖的一種，但不像諧波圖那樣是基於鐘擺原理，平託圖通常是用電動機驅動的（儘管也有一些是手搖的）。一些圓盤連桿在電動機上，連桿又連線在圓盤上，筆又連線到連桿上。連桿上的圓盤尺寸、連桿長度、連線點位置你都可以自已改動，電機的相對速度與和偏移量可以創造出一大堆不同型別的曲線。

很長時間內我都不知道「pintograph」這個名字是怎麼來的。最終發現是他創造了這個名詞，事實上是他的女兒。它是從「縮放儀pantograph」演變而來，這些轉動的輪子看起來像是一輛福特平託。閱讀這裡獲取更多 http://www.fxmtech.com/harmonog.html

以防你對縮放儀(pantograph)不熟悉，我解釋一下，這個裝置是一般是用來複制繪圖的。它有一些旋轉的連桿。將一個軸點固定住，將指示器指向這些軸點中的其實一個點，另一頭是固定的筆。 當你按原圖移動指示器，另一頭的筆就繪製出相同的形狀。你可以用它複製同樣的形狀或者調整複製時的大小。這是維基百科對縮放儀(pantograph)的解釋 https://en.wikipedia.org/wiki/Pantograph

模擬器

平託圖模擬起來相當簡單。它由兩個旋轉的轉盤用各自的連桿連連線。在它的反方向上兩根連桿連線在一起的點就是虛擬畫筆的位置，

首先，我們得先模擬兩個盤。它們擁有各自的 x, y 位置，半徑，速度和相位。我們將兩個盤都變成視覺化以便讓你知道到是如何執行的。另外它將會是一個非常長且複雜的公式。

我們將建立兩個旋轉的圓，且在圓周上顯示那個連桿連線的點。

每個圓盤將用以下結構表示：

disk: {
  x,
  y,
  radius,
  speed,
  phase,
}

就像之前一樣，我們不管它是一個通用物件、結構、類或其它什麼的來表示。並且我假定你已經有一個函數用於建立返回這樣的結構：

d0 = disk(100, 200, 100, 2, 0.5)
d1 = disk(400, 200, 60, 3, 0.0)

現在我們可以像下面這樣設定一個動畫：

width = 600
height = 400
canvas = (width, height)
t = 0
 
d0 = disk(100, 200, 100, 2, 0.5)
d1 = disk(400, 200, 60, 3, 0.0)
 
function loop() {
  clearScreen()
 
  circle(d0.x, d0.y, d0.radius)
  stroke()
  x0 = circle.d0.x + cos(t * d0.speed + d0.phase) * d0.radius
  y0 = circle.d0.y + sin(t * d0.speed + d0.phase) * d0.radius
  circle(x0, y0, 4)
  fill()
 
  circle(d0.x, d0.y, d0.radius)
  stroke()
  x1 = circle.d1.x + cos(t * d1.speed + d1.phase) * d1.radius
  y1 = circle.d1.y + sin(t * d1.speed + d1.phase) * d1.radius
  circle(x1, y1, 4)
  fill()
 
  t += 0.1
}

（譯者注：注意原作者在虛擬碼中有個小錯誤，即下面 y0, y1 內也使用了 cos 來計算，我已將其改為 sin ）

再一次強調一下，loop 是個假定的函數代表的是無限迴圈用於建立動畫。我自己用程式碼實現了 loop 建立了一個幀動畫，下面是我弄的 gif 圖，但它也可以是一個實時動畫：

它雖然不是那麼絲滑，但不重要。我們有了兩個不同大小、速度的圓。 程式碼本身並不複雜。我們先清空了螢幕，然後在兩個圓的圓周位置上各自繪製一個圓。它用於連線連桿。這裡應用基礎的三角學：x = cos(angle) * radius, y = sin(angle) * radius, 角度是用 t * 速度 + 相位。 這樣就得到了那兩個點，我們用實心小圓代表。連線連桿並找到那根虛擬筆的位置

接下來事情變的更加數學化了。我們需要兩個連線杆。每個連線杆都應該各自連線到一個旋轉的點上。然後它們的另一端彼此相連。像下面草圖畫的那樣：

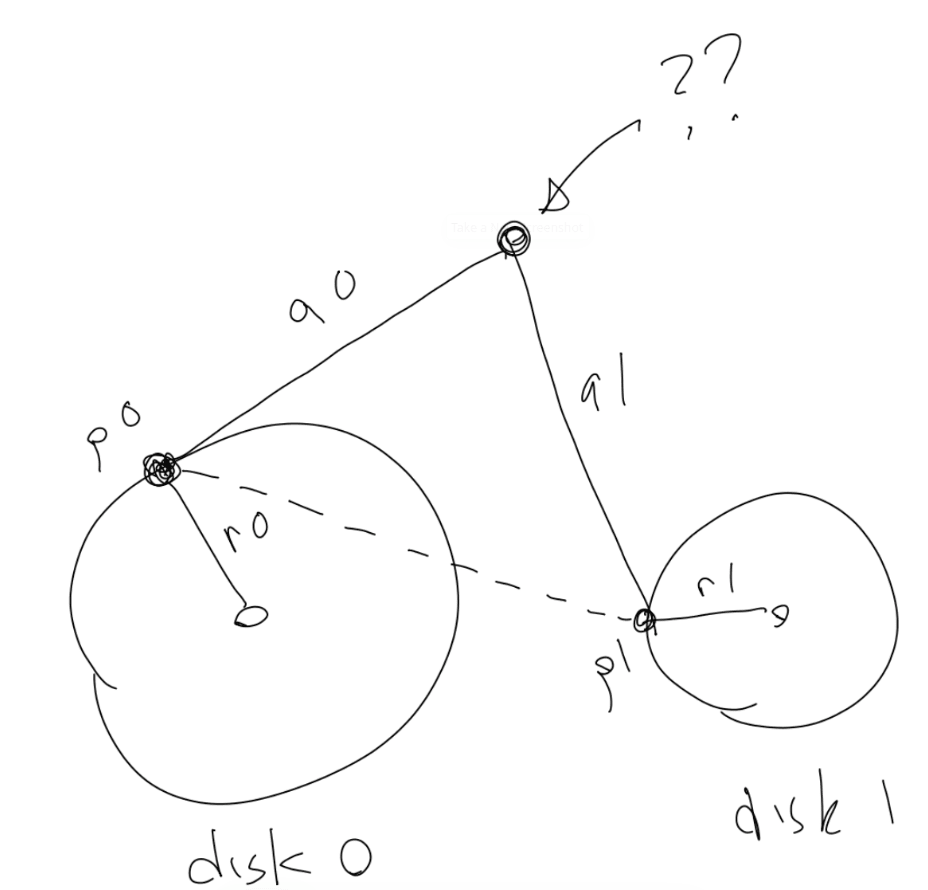
兩個圓盤。通過兩個圓盤的半徑，旋轉和位置，這 p0 和 p1 也就知道了。這就是我們上面做的。 我們也可以直接定義連桿長度。它們現定義成等長， 它當然也可以不等長。 我們把它命名成 a0 和 a1.(我知道它們現在草圖中看起來像 90 和 91 sorry!), 我們需要計算是的兩個連桿連線點的位置。

p0 和 p1 之間的距離我們通過勾股定理很容易計算出來。我們把它命名為 d 。在圖中用虛線表示。

現在我們擁有了一個三角形，每一邊分別為 a0, a1 和 d。

這裡有個三角法則叫「餘弦定理」能幫我們。如果你知道三角形的三條邊, a, b 和 c, 那麼我們就可以計算得到三個角的角度。通常被寫成下面這樣：

c = sqrt(a*a + b*b - 2*a*b*cos(y))

y 是 c 邊的對角。所以如果你知道兩邊的長度和它們的夾角，那麼你就能算出它夾角的對邊長度。儘管它非常有用，但我們這裡暫時用不到。

我們可以重新整理公式，讓未知道的變數在一邊，另一邊則是可計算的公式。

我們需要知道三個角中的其中一個角用於計算虛擬筆的位置。下面是我用餘弦定理公式手動計算的代數結果公式。

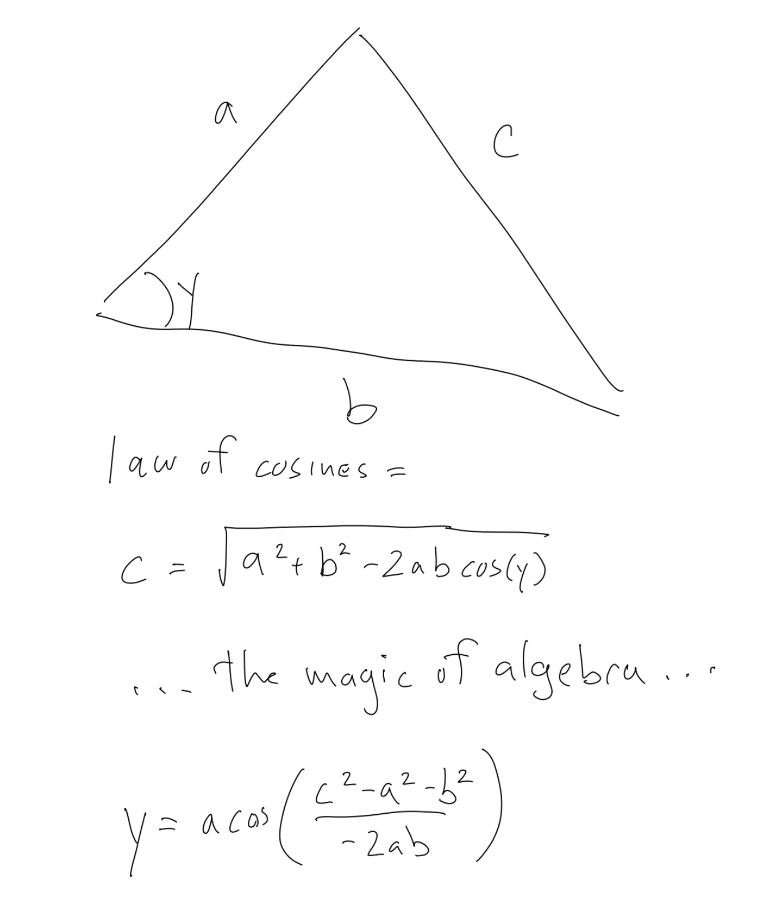
在我們例子中，三邊在餘弦定理公式中對應關係如下：

a = a0
b = d
c = a1

應用公式後，我們就可以得到 角 p1-p0-pen 的夾角了.

我們也能用 atan2 得到 p0 到 p1 的角度。兩者相關就得到了 p0 到 pen 的角度。

再次，展示下我畫的草圖

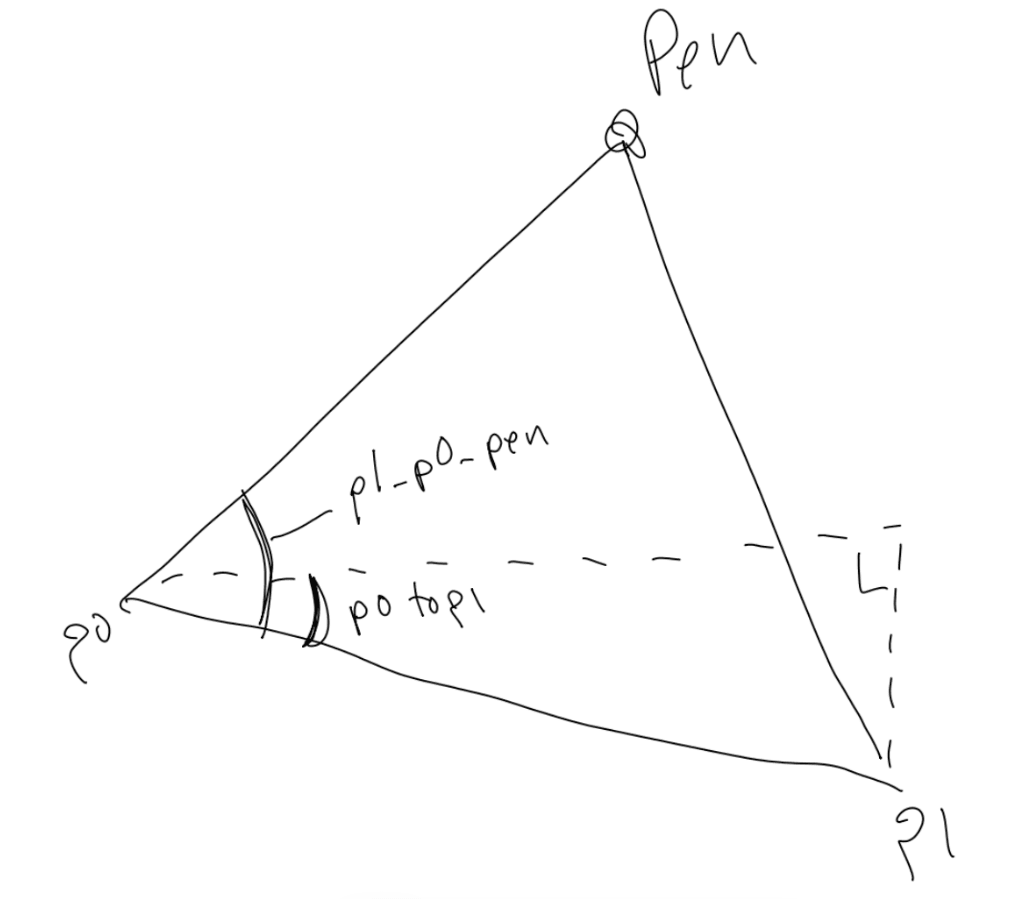
通過餘弦定理得到 大角 p1 到 p0 到 pen 的夾角 我們把它命名為 p1_p0_pen. 通過 atan2 計算出的小的那個角命名為 p0toP1。相減后角的值，就指向虛擬筆的位置。我相信有很多種方式可以計算出這個角， 也許比我這種方式更好， 但我這種方式可以正常執行。你可以繼續簡化它，但我用詳細的步驟用於說明，希望對你有幫助。

下面是程式碼部分：

width = 600
height = 600
canvas = (width, height)
t = 0
 
d0 = disk(150, 450, 100, 2, 0.5)
d1 = disk(450, 450, 60, 3, 0.0)
 
function loop() {
  clearScreen()
 
  circle(d0.x, d0.y, d0.radius)
  stroke()
  x0 = d0.x + cos(t * d0.speed + d0.phase) * d0.radius
  y0 = d0.y + sin(t * d0.speed + d0.phase) * d0.radius
  // （譯者注：左側大圓圓周上的小圓）
  circle(x0, y0, 4)
  fill()
  
  // (譯者注：原作者此處 circle(d0.x, d0.y, d0.radius); 書寫錯誤 ，應為 circle(d1.x, d1.y, d1.radius))
  circle(d1.x, d1.y, d1.radius)
  stroke()
  x1 = d1.x + cos(t * d1.speed + d1.phase) * d1.radius
  y1 = d1.y + sin(t * d1.speed + d1.phase) * d1.radius
  circle(x1, y1, 4)
  fill()
 
  // 連桿長度
  a0 = 350
  a1 = 350
 
  // p0 和 p1 距離
  dx = x1 - x0
  dy = y1 - y0
  d = sqrt(dx * dx + dy * dy)
 
  // 找到兩個關鍵角相減
  p1_p0_pen = acos((a1 * a1 - a0 * a0 - d * d) / (-2 * a0 * d))
  p0toP1 = atan2(y1 - y0, x1 - x0)
  angle = p0toP1 - p1_p0_pen
 
  // 計算得到虛擬筆的位置
  //（譯者注：左側大圓圓周上的小圓位置和上面的angle 計算出虛擬筆的位置）
  pX = x0 + cos(angle) * a0
  pY = y0 + sin(angle) * a0
   
  // 繪製連桿
  moveTo(x0, y0)
  lineTo(pX, pY)
  lineTo(x1, y1)
  stroke()
 
  t += 0.1
}

按上面的程式碼正確編碼後你應該可以渲染出如下的結果：

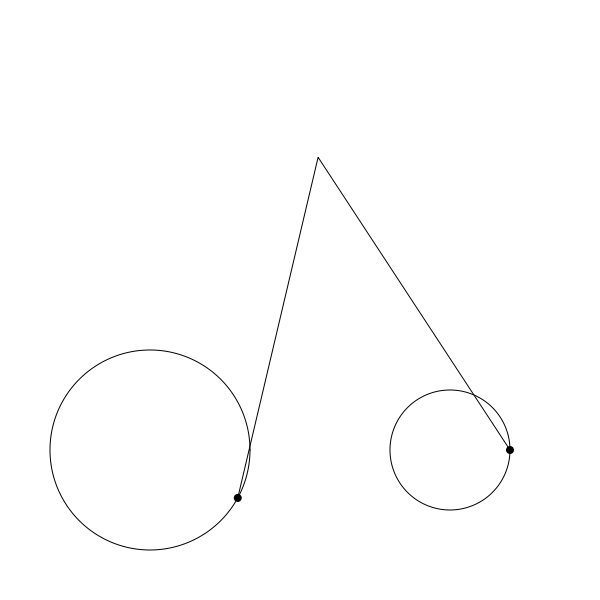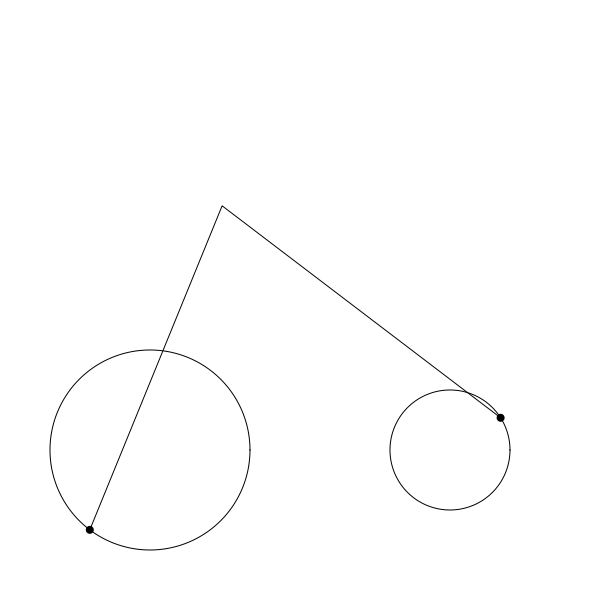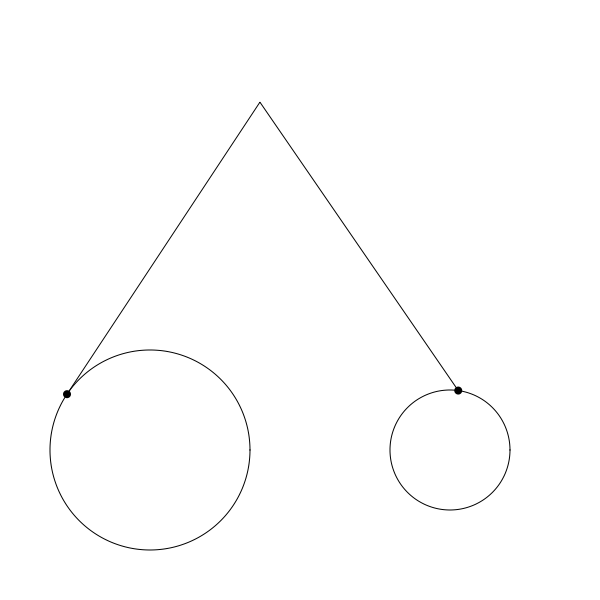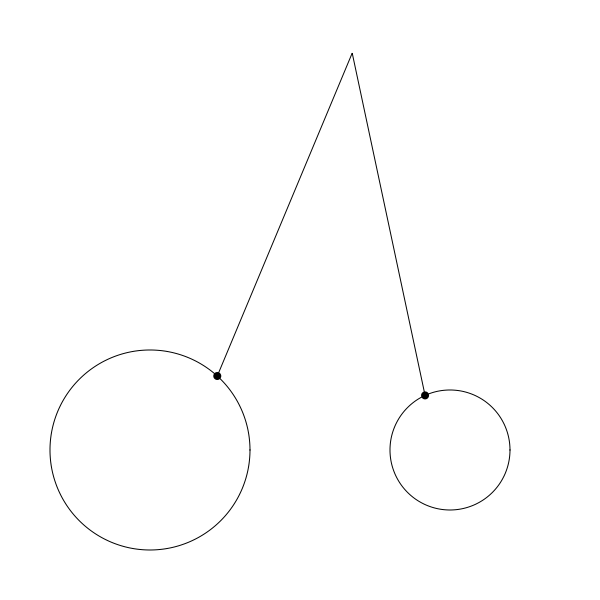
再次提醒，這只是不完整迴圈的 gif 圖，僅用於演示如何執行。程式碼中每一步都有註釋。希望對你有幫助。 注意我也改了 canvas 的寬高並且將圓盤位置調整到了底部騰出空間用於顯示完整的連桿。

有一點需要注意，要確保連桿足夠的長保證它們能彼此相連。在真實世界中，如果它們太短，可能會卡住或弄壞電動機。 在我們的模擬中，在反餘弦函數計算 acos 可能會得到 NaN （not a number）錯誤，而你可能還摸不著頭腦。我這是經驗之談。

繪製曲線

最後讓我們看看畫出個啥。在此，我把動畫禁掉並且也不繪製圓和連桿 。我將追蹤每次迭代虛擬筆的路徑用於繪製一個長迴圈的具有利薩茹特徵的曲線。

width = 800
height = 600
canvas = (width, height)
 
function render() {
  t = 0
   
  d0 = disk(250, 550, 141, 2.741, 0.5)
  d1 = disk(650, 550, 190, 0.793, 0.0)
 
  // the length of the arms
  a0 = 400
  a1 = 400
   
  for (i = 0; i < 50000; i++) {
    x0 = d0.x + cos(t * d0.speed + d0.phase) * d0.radius
    y0 = d0.y + sin(t * d0.speed + d0.phase) * d0.radius
 
    x1 = d1.x + cos(t * d1.speed + d1.phase) * d1.radius
    y1 = d1.y + sin(t * d1.speed + d1.phase) * d1.radius
 
    // get the distance between p0 and p1
    dx = x1 - x0
    dy = y1 - y0
    d = sqrt(dx * dx + dy * dy)
 
    // find the two key angles and subtract them
    p1_p0_pen = acos((a1 * a1 - a0 * a0 - d * d) / (-2 * a0 * d))
    p0toP1 = atan2(y1 - y0, x1 - x0)
    angle = p0toP1 - p1_p0_pen
 
    // find the pen point
    pX = x0 + cos(angle) * a0
    pY = y0 + sin(angle) * a0
   
    lineTo(pX, pY)
    t += 0.01
  }
  stroke()
}

我留了足夠多的空間讓你自己去優化程式碼，少年加油！儘管程式碼看起來亂糟糟的，但繪製結果它應該會像下圖：

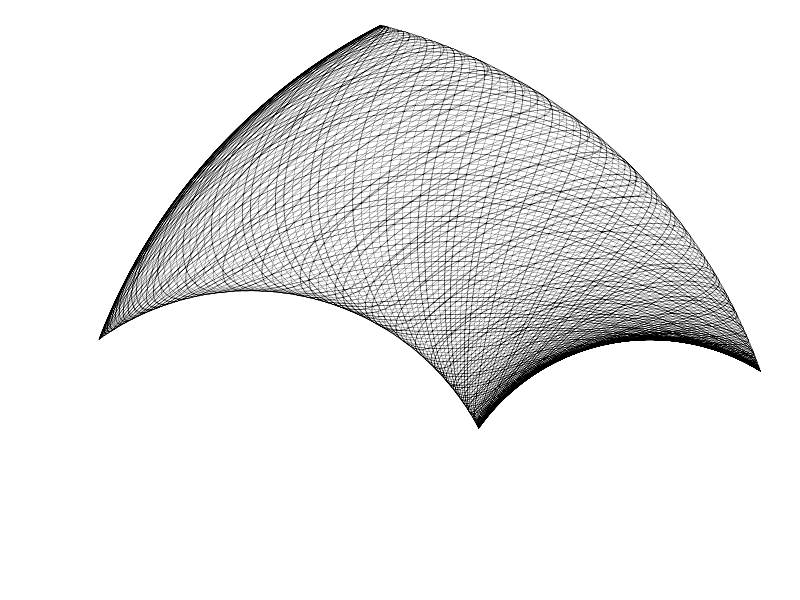
這裡你可以嘗試修改程式碼中的許多東西用於體驗。這就是一個超簡易的平託圖，所以上面的圖看起來大多都有點糙。但你可以依據這些原則建立各種更復雜的裝置模擬。這個網站擁有許多 demo 相信可以啟發你的思路：

https://michaldudak.github.io/pintograph/demo/

一個盤疊一個盤， 旋轉的平託圖，三個轉盤的平託圖，等等。

如果你想開始嘗試，你只需要在 youtube 搜尋 「harmonograph」, 「pintograph」 and 「drawing machines」 等關鍵字，它會提供無限的點子給你----你可以用來編碼或弄個真實的裝置。在我看來最有趣的那一個例子是一個轉檯上自身慢慢旋轉在一張紙上繪製出曲線。

總結

利薩茹曲線和相關的模擬裝置討論在這裡就結束了。至少暫時就這樣了。下一章我們將回歸到比較基礎的標準幾何曲線。

本章 Javascript 原始碼 https://github.com/willian12345/coding-curves/blob/main/examples/ch06

---

部落格園: http://cnblogs.com/willian/
github: https://github.com/willian12345/