前言

在上一篇文章中，給大家介紹了氣泡排序和選擇排序，這兩種演演算法都是排序演演算法。實際上排序演演算法還有插入、希爾、快速排序等，接下來我們就來學習一下這幾種排序演演算法。

---

全文大約【5400】 字，不說廢話，只講可以讓你學到技術、明白原理的純乾貨！本文帶有豐富的案例及配圖視訊，讓你更好地理解和運用文中的技術概念，並可以給你帶來具有足夠啟迪的思考......

一. 直接插入排序

1. 概念

直接插入排序(Insertion Sort) ，顧名思義就是把未排序的元素一個一個地插入到有序的集合中，插入時把有序集合從後向前掃一遍，找到合適的插入位置。 為了讓大家更好地理解插入排序，通過一個簡單的例子給大家解釋一下插入排序的含義，我們以日常生活中的紙牌遊戲為例：

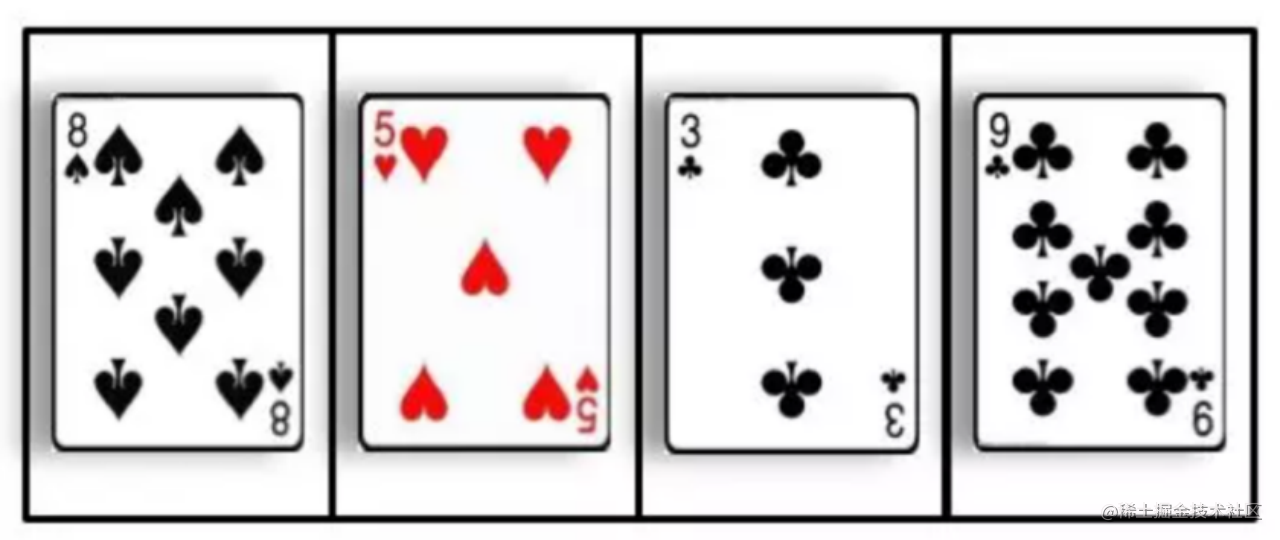
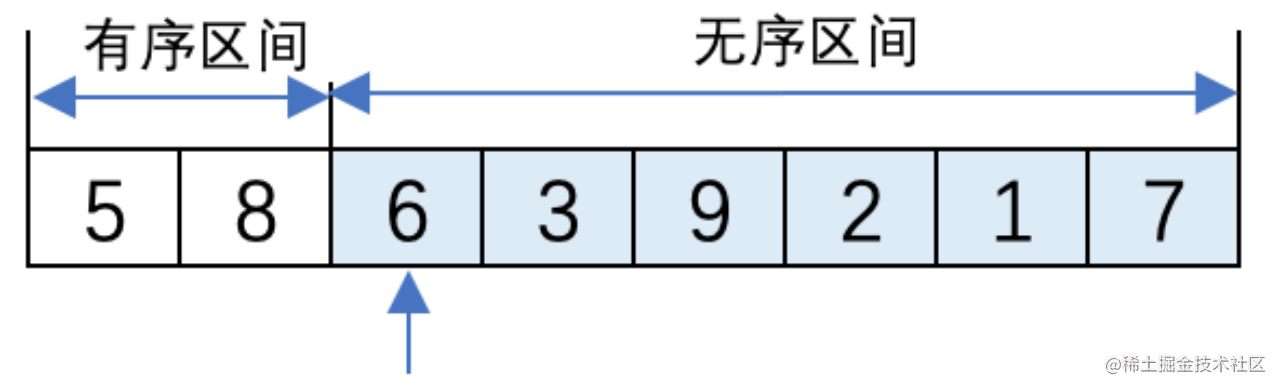
(2) 將無序區間的第一個元素8插入到有序區間的數列末尾，8和5比較大小，8比5大則無需交換位置。此時有序區間中的元素是5、8，無序區間中有6、3、9、2、1、7。

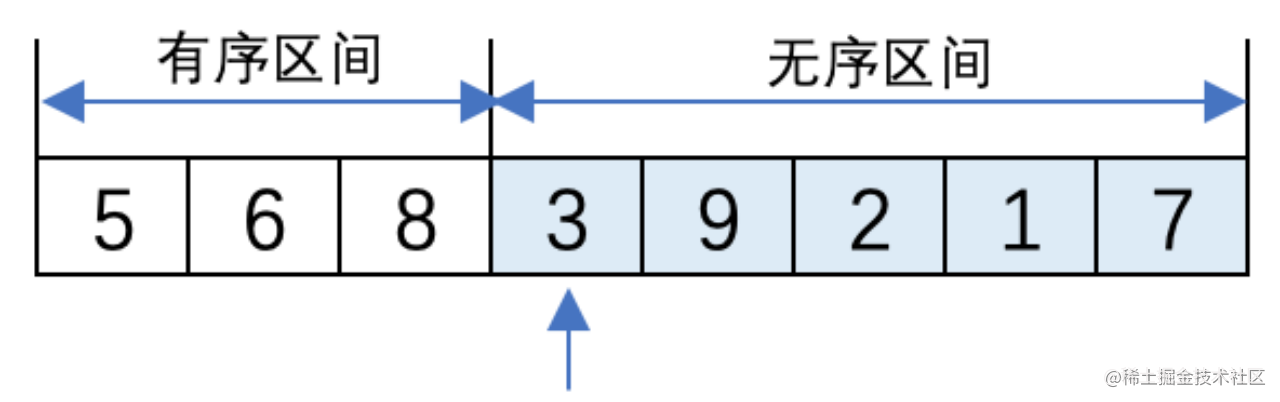
(3) 將無序區間的第一個元素6插入到有序區間的末尾，形成5、8、6的排列順序。6和左側的8比較大小，6比8小則換位；6再與5比較，6比5大則無需換位。最後有序區間中形成了5、6、8的排列。此時，無序區間中還有3、9、2、1、7。

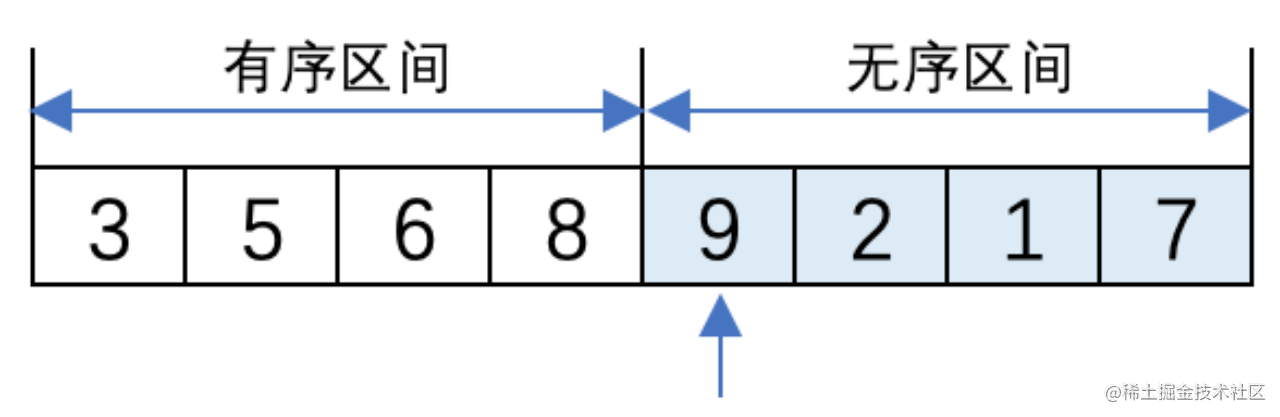
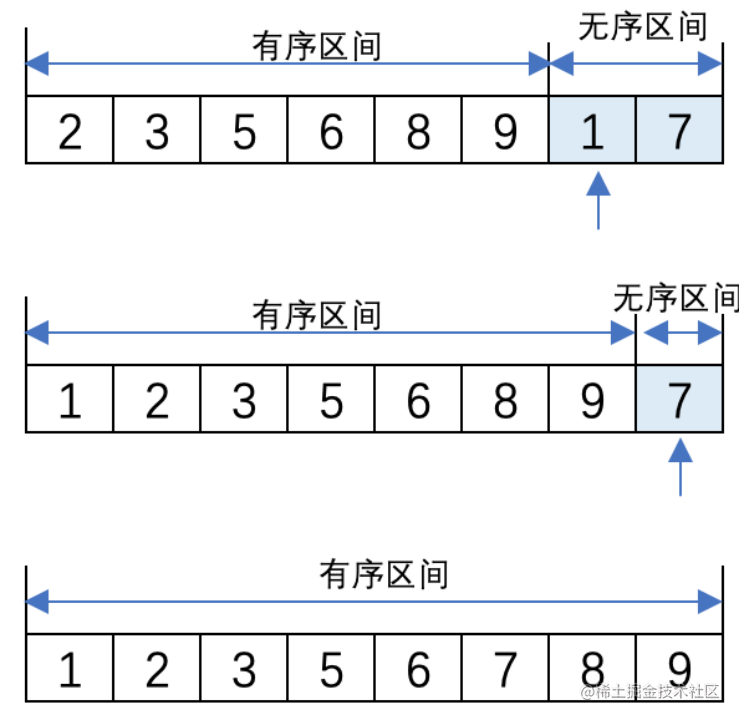
(4) 將無序區間的第一個元素3插入到有序區間的末尾，形成5、6、8、3的排列順序。3和左側的8比較大小，3比8小則換位；3再與6比較大小，3比6小則繼續換位；3與5比較大小，3比5小繼續換位。最後形成3、5、6、8的排列，此時，有序區間中是3、5、6、8，無序區間中還有9、2、1、7。

（5) 然後依次類推，直到無序區間為空時，排序結束。最終排序的結果為：1、2、3、5、6、7、8、9。

4. 程式設計實現

接下來我們使用Java語言，對插入排序演演算法進行程式設計實現：

public static void insertionSort(int[] arr) {
    int loop = 0;
    int count = 0;
    //對陣列進行遍歷
    for (int i = 0; i < arr.length; i++) {
        //第二個迴圈僅僅是將當前資料跟自己左邊的數位進行比較，如果小於左邊數位則交換位置，否則位置不變。
        for (int j = i; j > 0; j--) {
            count++;
            //此處使用break比使用if效率高，兩者在比較次數上有差別。
            if (arr[j] >= arr[j - 1]) break;
            // 前後兩個資料交換位置
            arr[j] = arr[j] + arr[j - 1] - (arr[j - 1] = arr[j]);
        }
    }
}

5. 總結

接下來我們把插入排序的特性總結一下。

5.1 時間複雜度

根據給定的數列的混亂程度，時間複雜度可做如下分析：

(1) 當數列本身是有序的，插入排序的時間複雜度是O(n)。原因是如果數列本身是有序，插入排序需要將每相鄰的兩個數位各比較一次，總共比較n-1次， 所以時間複雜度是O(n)。

(2) 當數列是無序的，最壞的情況下需要比較n(n-1)/2次，所以時間複雜度是O(n²)。

5.2 空間複雜度

(1) 插入排序是原地排序，其空間複雜度是O(1)。

(2) 插入排序中，無序區間的元素在插入到有序區間的過程中，是依次與左側的元素比較，如果兩個元素相等，則不交換位置。

5.3 插入排序的適用場景

(1) 一個有序的大陣列中融入一個小陣列，比如有序大陣列[1, 2, 3, 4, 5, 6, 7, 8, 9}中融入一個小陣列[0, 1]。

(2) 陣列中只有幾個元素的順序不正確，或者說陣列部分有序。

總結來說，插入排序是一種比較簡單直觀的排序演演算法，適用於處理資料量比較小或者部分有序的數列。

二. 快速排序

1. 概念

快速排序(Quick Sort) ，其是對氣泡排序的一種改進，該演演算法由霍爾(Hoare)在1962年提出。與氣泡排序一樣，快速排序也屬於交換排序演演算法，通過元素之間的比較和交換位置來達到排序的目的。

快速排序每次排序的時候設定一個基準點，將小於基準點的數全部放到基準點的左邊，將大於等於基準點的數全部放到基準點的右邊。這樣每次交換的時候就不會像氣泡排序一樣只能在相鄰的兩個數之間進行交換，交換的距離就得到提升。快速排序之所比較快，因為相比氣泡排序，每次交換是跳躍式的。這樣總的比較和交換次數就少了，排序效率自然就提高了。

通過一趟排序，將要排序的資料分割成兩部分，其中一部分的所有資料都比另外一部分的所有資料都要小，然後再按此方法對這兩部分資料分別進行快速排序，整個排序過程遞迴進行，以此達到整個資料變成有序序列。快速排序演演算法的實現思路就是分治思想的應用。

2. 實現思路

快速排序基於遞迴的方式來實現，其實現思路如下：

(1) 選定一個合適的值(理想情況是選擇數列的中值最好，但為了實現方便一般都是選擇數列的第一個值)，稱為「基準元素」(pivot)。

(2) 基於基準元素，將數列分為兩部分，較小的分在左邊，較大的分在右邊。

(3) 第一輪下來，這個基準元素的位置一定在最終位置上。

(4) 對左右兩個子數列分別重複上述過程，直到每個子數列中只包含一個元素則排序完成。快速排序的核心思想就是在給基準元素找正確的位置。

3. 實現步驟

接下來通過一個範例來講解快速排序的步驟。

假設現在有一個亂序陣列[5，8，6，3，9，2，1，7]，我們使用快速排序演演算法進行排序。首選要選擇一個元素作為基準元素，在此例中，我們可以選擇首元素5作為基準元素。接下來進行元素的交換，具體步驟如下：

(1) 選定基準元素5，同時設定兩個指標分別為left和right，分別指向最左側元素5、最右側元素7。移動和比較的規則是：

• 從right指標的位置開始，讓指標指向的元素和基準元素做比較。right指標指向的資料如果小於基準元素，則right指標停止移動；切換至left指標，否則right指標繼續向左移動。

• 輪到left指標移動時，讓left指標指向的元素與基準元素做比較。將left指標指向的資料和基準元素做比較。left指向的元素資料如果大於基準元素，則left指標停止移動，否則left指標繼續向右移動。

• 將left和right指標指向的元素交換位置。

(2) right指標先開始，right指標當前指向的資料是7，由於7>5，right指標繼續左移，指向到1，由於1<5，停止在1的位置。

• 輪到left指標。由於left開始指向的是基準元素5，所以left右移1位，指向到8。由於8>5，所以left指標停下

• 接下來，left和right指向的元素進行交換。此時形成數列為[5, 1, 6, 3, 9, 2, 8, 7]

(3) 重新切換到right指標，指標向左移動，right指標指向到2。由於2<5，right指標停止在2的位置。

• 輪到left指標，指標右移1位，指向到6，由於6>5，所以left指標停下。

• 接下來，left和right所指向的元素進行交換。此時形成數列為[5, 1, 2, 3, 9, 6, 8, 7]。

(4) 重新切換到right指標，指標向左移動。right指標指向到9，由於9>5，right指標繼續左移，指向到3，由於3<5，則right指標停止在3的位置。

• 輪到left指標，指標右移1位，指向到3，此時right指標和left指標重疊在一起。

• 接下來，將pivot元素5與重疊點的元素3進行交換，此時形成數列為[3, 1, 2, 5, 9, 6, 8, 7]。第一輪排序結束。

我們把上述的文字描述過程，做成對應的示意圖，如下所示：

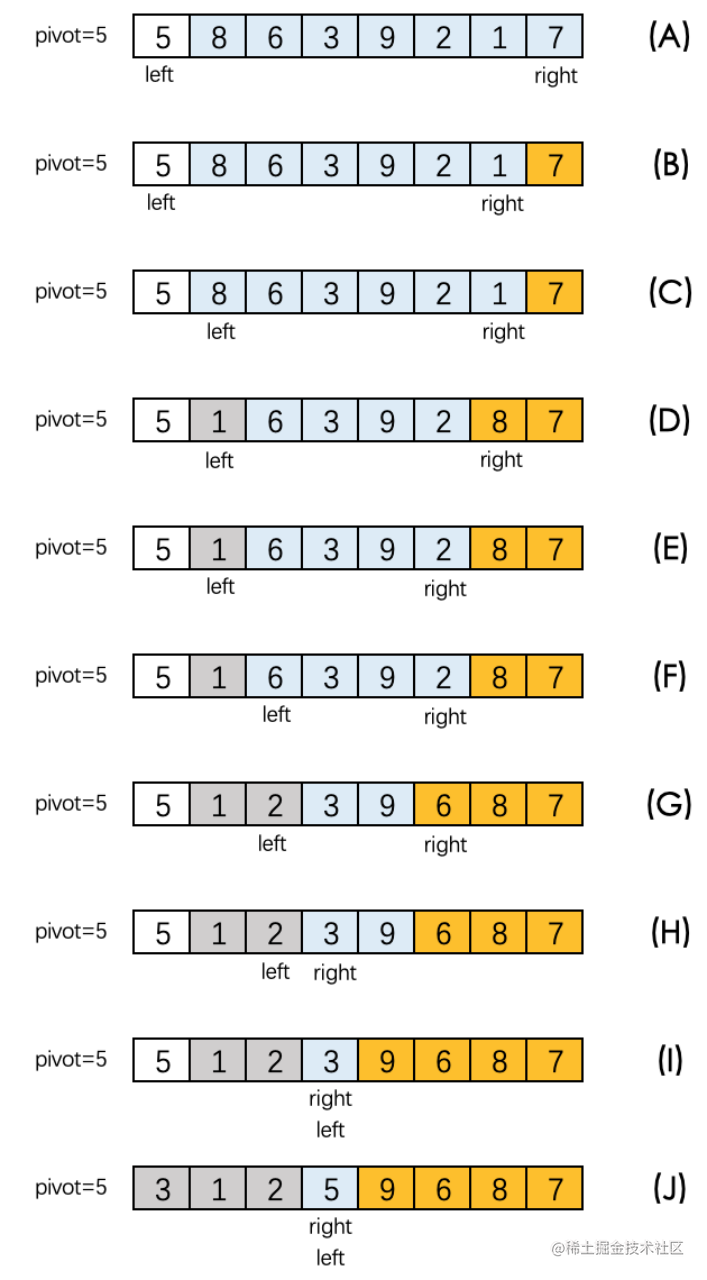
第一輪排序結束後，本輪的基準元素5的位置，就是最終排序後所在的位置。接下來，我們採用遞迴的方式，分別對基準元素5左側的前半部分[3, 1, 2]進行排序，再對元素5右側的後半部分[9, 6, 8, 7]進行排序，如下圖所示：

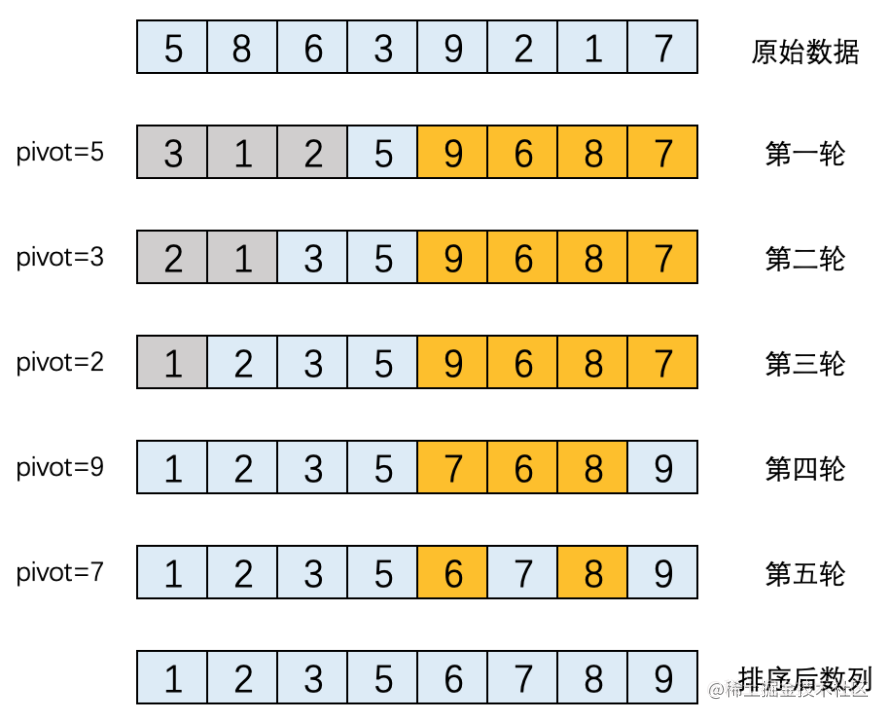
(1) 基準元素5的前半部分[3, 1, 2]，以3為基準元素，經過排序，結果為[2, 1, 3]。本輪下來，本輪的基準元素3的位置就是其最終位置。

(2) 上輪基準元素3左側的佇列[2, 1]，以2為基準元素排序，排序結果為[1, 2]。本輪下來，本輪的基準元素2的位置就是其最終位置。

(3) 上輪基準元素2左側只剩下元素1，1就是自己的基準元素。這樣元素1的最終位置就確定了。

(4) 基準元素5的後半部分[9, 6, 8, 7]，以9為基準元素進行排序，結果為：[7, 6, 8, 9]，本輪下來，本輪的基準元素9的位置就是其最終位置。

(5) 上輪基準元素9左側的佇列[7, 6, 8]，以7為基準元素進行排序，結果為[6, 7, 8]。本輪下來，本輪的基準元素7的位置就是其最終位置。

(6) 上輪基準元素7左側只剩下6，6就是自己的基準元素。這樣元素6的最終位置就確定了。

(7) 基準元素7右側只剩下8，8就是自己的基準元素。這樣元素8的最終位置就確定了。

(8) 此時基準元素5、3、2、1、9、7、6、8都找到其正確的位置，則排序結束。

4. 編碼實現

接下來我們使用Java語言對快速排序演演算法進行程式碼實現：

public static void quickSort(int[] arr, int start, int end) {
    // 遞迴結束條件:start大於或等於end時
    if (start < end) {
        // 得到基準元素位置
        int pivotIndex = partition(arr, start, end);
        // 根據基準元素，分成兩部分進行遞迴排序
        quickSort(arr, start, pivotIndex - 1);
        quickSort(arr, pivotIndex + 1, end);
    }
}

private static int partition(int[] arr, int start, int end) {
    // 取第1個位置的元素作為基準元素
    int pivot = arr[start];
    int left = start;
    int right = end;

    while (left < right) {
        //right指標左移
        while (left < right && arr[right] >= pivot) right--;
        //left指標右移
        while (left < right && arr[left] <= pivot) left++;
        if (left >= right) break;
        //交換left和right 指標所指向的元素
        arr[left] = arr[left] + arr[right] - (arr[right] = arr[left]);
    }
    // 將基準元素與指標重合點所指的元素進行交換
    arr[start] = arr[left];
    arr[left] = pivot;
    
    return left;
}

這裡使用了兩個方法quickSort和partition實現快速排序演演算法的邏輯，其核心思路與前文描述一致，先找到一個元素作為基準元素，然後再分開進行排序。

三. 希爾排序

1. 概念

希爾排序(Shell’s Sort) ，該演演算法是插入排序的一種，又稱「縮小增量排序」(Diminishing Increment Sort) ，希爾排序是Shell在1959年提出的。

希爾排序是基於直接插入排序進行改進而形成的排序演演算法。 它是直接插入排序演演算法的一種更高效的改進版本。直接插入排序本身還不夠高效，插入排序每次只能將資料移動一位。當有大量資料需要排序時，會需要大量的移位元運算。但是插入排序在對幾乎已經排好序的資料操作時，效率很高，幾乎可以達到線性排序的效率。所以，如果能對資料進行初步排列達到基本排序，然後再用插入排序就會大大提高排序效率。希爾排序正是基於此思路而形成的。

2. 實現步驟

希爾排序的步驟簡述如下：

(1) 把元素按步長gap分組，gap的數值其實就是分組的個數。gap的起始值為數列長度的一半，每回圈一輪gap減為原來的一半。

(2) 對每組元素採用直接插入排序演演算法進行排序。

(3) 隨著步長逐漸減小，組就越少，組中包含的元素就越多。

(4) 當步長值減小到1時，整個資料合成一組，最後再對這一組數列用直接插入排序進行最後的調整，最終完成排序。

我們以無序數列[5，8，6，3，9，2，1，7，,4]為例，詳細介紹希爾排序的步驟：

(1). 第一輪排序，gap = length/2 = 4，即將陣列分成4組。四組元素分別為[5，9，4]、[8，2]、[6，1]、[3，,7]。對四組元素分別進行排序結果為：[4，5，9]、[2，8]、[1，6]、[3，7]。將四組排序結果進行合併，得到第一輪的排序結果為：[4，2，1，3，5，8，6，7，9]。如下圖所示。

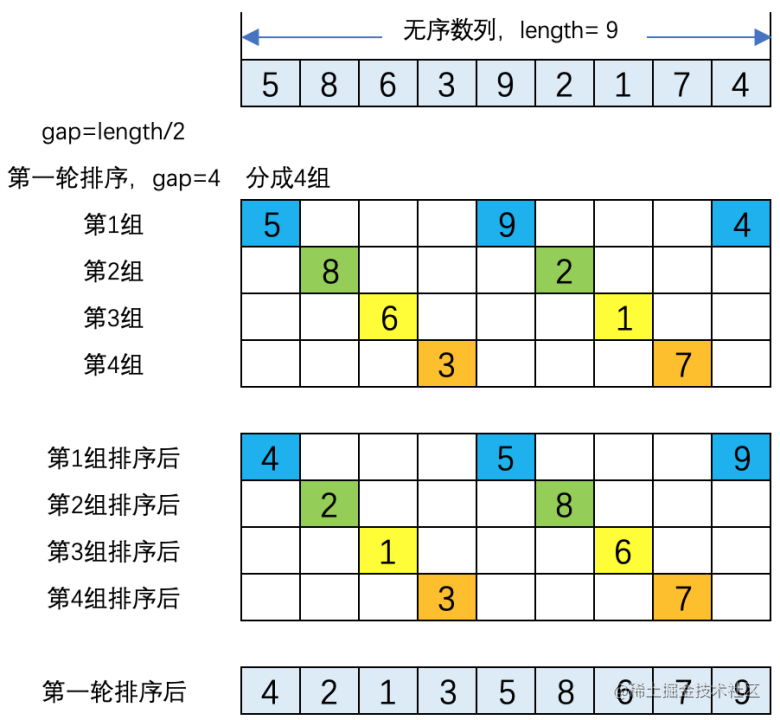
(2). 第二輪排序，gap = 2，將數列分成2組。兩組的元素分別是[4，1，5，6，9]和[2，3，8，,7]。這兩個組分別執行直接插入排序後的結果為[1，4，5，6，9]和[2，3，7，8]。將兩組合並後的結果為[1，2，4，3，5，7，6，8，9]，如下圖所示。

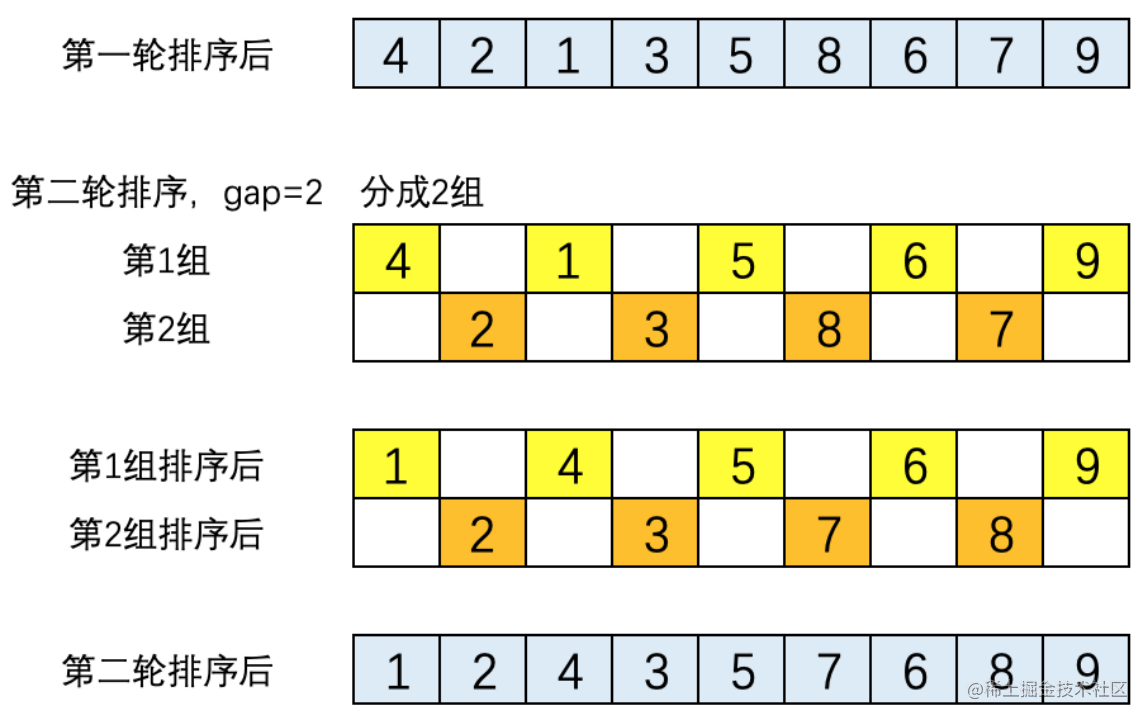
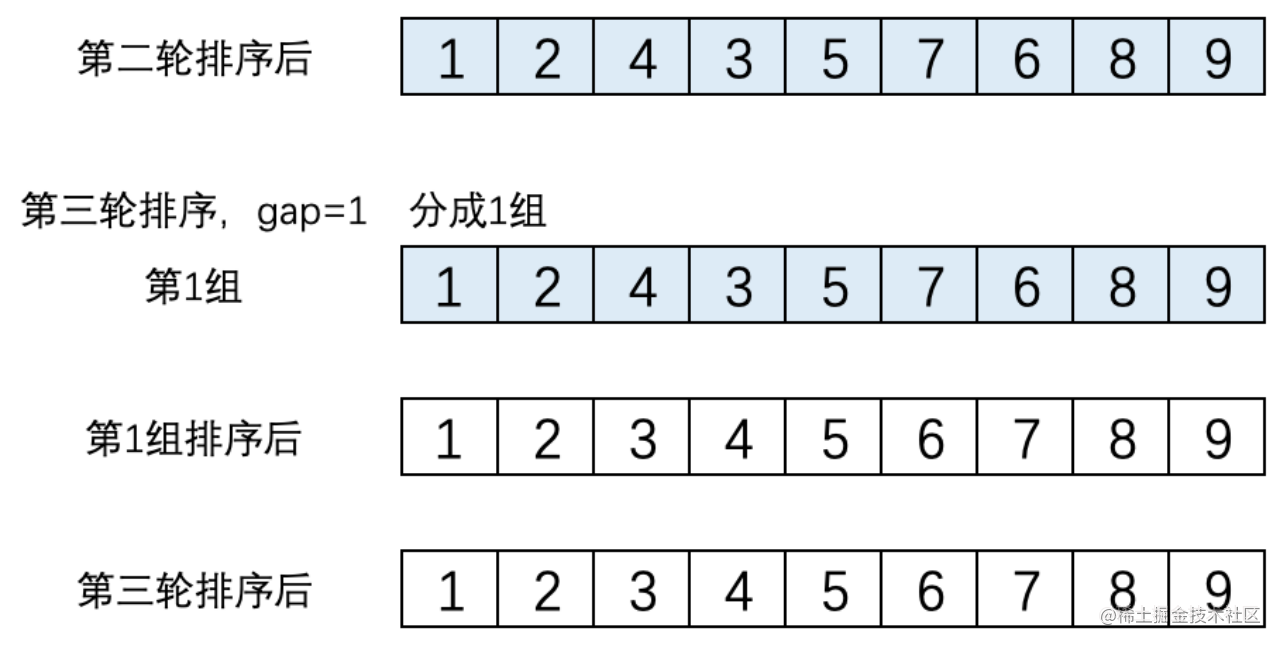
(3). 第三輪排序，gap = 1，陣列就變成了一組。 該組的元素是[1，2，4，3，5，7，6，8，9]，這個組執行直接插入排序後結果為[1，2，3，4，5，6，7，8，9]，這個結果就是第三輪排序後得到的結果。此時排序完成，如下圖所示。

3. 編碼實現

接下來我們用程式碼對希爾排序進行程式設計實現：

public static void shellSort(int[] arr) {
    int loop = 0;
    //增量gap，並逐步縮小增量
    for (int gap = arr.length / 2; gap > 0; gap /= 2) {
        //對一個步長區間進行比較 [gap,arr.length)
        for (int i = gap; i < arr.length; i++) {
            //對步長區間中具體的元素進行比較
            for (int j = i - gap; j >= 0; j -= gap) {
                //System.out.println("j=" + j);
                if (arr[j] <= arr[j + gap]) break;
                //換位
                arr[j] = arr[j] + arr[j + gap] - (arr[j + gap] = arr[j]);
            }
        }
    }
}

4. 總結

接下來我們再把希爾排序的複雜度等情況進行分析總結，如下：

(1) 希爾排序的時間複雜度與增量(即步長gap)的選取有關。例如，當增量為1時，希爾排序退化成了直接插入排序，此時最壞情況時間複雜度為O(n²)。而具有增量的希爾排序的平均時間複雜度為O(n^1.3)，希爾排序最好情況時間複雜度是O(n)。

(2) 希爾排序的空間複雜度是O(1)。

(3) 直接插入排序是穩定的，不會改變相同元素的相對順序。 但在不同的插入排序過程中，相同的元素可能在各自的插入排序中移動，最後其穩定性就會被打亂。也就是說，對於相同的兩個數，可能分在不同的組中而導致它們的順序發生變化，所以希爾排序是不穩定的。

---

四. 結語

至此，我們我們已經向大家介紹了氣泡排序、選擇排序、插入排序、快速排序、希爾排序等五種經典的排序演演算法。除此以外，還有堆排序、歸併排序、桶排序、計數排序等一些經典的排序演演算法。

大家會發現，我們介紹排序演演算法的步驟和過程都是相同的，基本都包含演演算法概念、思想和原理、演演算法步驟，以及編碼實現等幾個部分。

在本篇的最後，我們給大家總結出經典的排序演演算法的對比和總結，我們從時間複雜度、空間複雜度、穩定性等幾個方面進行橫向總結。

排序演演算法	時間複雜度(平均)	時間複雜度(最壞)	時間複雜度(最好)	空間複雜度	穩定性
氣泡排序	O(n2)	O(n2)	O(n)	O(1)	穩定
選擇排序	O(n²)	O(n²)	O(n²)	O(1)	不穩定
插入排序	O(n²)	O(n²)	O(n)	O(1)	穩定
快速排序	O(nlogn)	O(n²)	O(nlogn)	O(nlogn)	不穩定
堆排序	O(nlogn)	O(nlogn)	O(nlogn)	O(1)	不穩定
希爾排序	O(n^1.3)	O(n²)	O(n)	O(1)	不穩定
歸併排序	O(nlogn)	O(nlogn)	O(nlogn)	O(n)	穩定
桶排序	O(n+k)	O(n²)	O(n)	O(n+k)	穩定
計數排序	O(n+k)	O(n+k)	O(n+k)	O(n+k)	穩定
基數排序	O(d(n+k))	O(d(n+k))	O(d(n+k))	O(n+k)	穩定

---