曲線藝術程式設計 coding curves 第五章諧波圖形（諧振圖形） HARMONOGRAPHS

原作：Keith Peters https://www.bit-101.com/blog/2022/11/coding-curves/

譯者：池中物王二狗(sheldon)

blog: http://cnblogs.com/willian/

原始碼：github: https://github.com/willian12345/coding-curves

這一篇幅建立在對第四章利薩茹曲線的討論之上。事實上諧波圖形並不是一類曲線，它是一種用於繪製（模擬）利薩茹曲線的裝置。當我說一個裝置時，我的意思就是真實物理世界的一個裝置，它由繩子、鏈條、槓桿、筆、沙瓶、鐘擺或其它機械結構組成用於建立這些曲線。

真諧波圖形

我第一次碰到諧波圖形是在波士頓的一個科技館中。那是在我小時候眾多旅行中的一次。它是一個類似鐘擺，裝滿沙子的容器，沙子漏出來形成一條軌跡。這個視訊中展示的並不完全像我當時看到的，但基本差不多。直到多年後我才知道它叫諧波圖形 harmonograph

（譯者注：如果打不開視訊這裡我截了個圖，我小時候從未見過，不知道你大夥有沒有見過類似的東西，反正我是第一次見）

https://www.youtube.com/watch?v=uPbzhxYTioM

這個視訊值得觀看用於深入探討利薩茹圖形。通過一個槓桿，來回擺動所花費的時間就稱為週期，我們說過的 frequency 頻率放到後面再討論。在視訊的4分12秒處，視訊作者解釋了這個鐘擺裝置為什麼可以擁有兩個不同週期在它各自軸上。這就是為啥最後形成的圖形看起來像利薩茹曲線- 因為它本來就是！如果各自軸週期相同，則它可能會建立一個圓形，橢圓形，螺旋。技術上講這些仍然也是利薩茹圖形的一種，但我們感興趣的是此篇中的諧波圖。

這裡是另一個版本使用筆和紙

源自 https://en.wikipedia.org/wiki/Harmonograph

在這個例子中，筆不動，紙做週期擺動。但完成的是一樣的事情。

這裡有另一個視訊與此類似的的裝置，它則紙盒，線，和膠帶做成！

https://www.youtube.com/watch?time_continue=65&v=S92mZcNIS8w&embeds_referring_euri=https%3A%2F%2Fwww.bit-101.com%2F&source_ve_path=MjM4NTE&feature=emb_title

這是純粹的利薩茹曲線與機械的，基於擺動的諧波圖形關鍵不同點。鐘擺慢慢失能，擺動經過的距離越來越小。直到停擺在繪製的中心點。

而這種型別的諧波圖形可以產生一些有趣的圖形，你甚至可以用兩個鐘擺製作出更復雜的。

下面是一個相關的例子：

此處，紙和筆都安裝在鐘擺頂部，配重在桌底擺動。所以它們自動能產生複雜的曲線。

這個視訊就是一個非常魔幻的雙鐘擺，展示了它可以建立出驚人的圖形。也演示了不少特徵。

https://www.youtube.com/watch?v=_PdGcl1Ugl0&t=110s

模擬諧振

鑑於咱是一個聚焦於程式設計的網站，我就不解釋如何建一個物理的諧振裝置了。但這些裝置肯定遵循物理規則，並且物理規則的公式已被我們知曉。我們可以用這些公式直接建立虛擬的諧波圖形。

我們先從單鐘擺諧振版本入手，但開始之前我們先回顧一下我們的利薩茹公式:

x = A * sin(a * t + d)
y = B * sin(b * t)

A 和 B 是波在自各軸上的振幅， a 和 b 是頻率。 d 用於讓 x 和 y 脫離它們的相位。t 是時間引數。最初我們說 t 會是 0 至 2 * PI 區別，但後面我們會看到它會無窮增長。

為了改動到模擬諧振，我們要認識到各自軸它們由自己的相位，而不是隻有一個有相位，另一個...沒相位？所以我們將 d 變成兩個變數 p1 和 p2。

x = A * sin(a * t + p1)
y = B * sin(b * t + p2)

這依然會是一個利薩茹曲線，但有了多了一點點複雜的定義。為了完全模擬諧誫，我們先要模擬失能或者說摸擬衰減。為了更為精確，它會以額外的乘數的形式呈現：

e-d*t

... 或者說「e 的底的負 d 乘以 t 次方」指數

在程式碼中表現為：

pow(e, -d * t)

pow 方法在任何數學庫中都會有。

所以，這都是些啥？我們有了兩個新的變數 e and d。實現上 e 是個常數，又名尤拉數，約等於 2.71828。我會讓你自己去了解相關知識，但 e 確實廣泛存在於各種物理公式中。當然也存在於鐘擺衰減中。

到目前為止，你可能猜到 d 是那個衰減因子。我們將 d 設為成一個相當小的值比如 0.002 就挺不錯的。現在當 t 等於 0，那麼指數為 0，指數函數計算結果會為 1.0 。

當 t 不斷增長，比如每個迭代增加 0.01，指數會緩慢的負向增長。當 t 為 0.01，指數為 -0.00002, 指數函數結果將會衰減至 0.9999800002

100 次迭代後， t 會變為 1.0 衰減因子將會是 0.9980019987。 1000 次迭代後，它將是 0.9801986733。所以你可以觀察到它減小的非常慢。如果 d 增加，那麼衰減值會向0.0更快的進發。下面展示的是應用在諧振公式內：

x = A * sin(a * t + p1) * pow(e, -d1 * t)
y = B * sin(b * t + p2) * pow(e, -d2 * t)

注意，我用了 d1 和 d2 這樣你在各自軸就有它各自的振幅、頻率、相位和衰減因子了。

為了讓它歸位，當 t 增長時上面的等式會慢慢接近 0.0，意謂著 x 和 y 會越來越小接近 0.0，模擬鐘擺擺動至停止。 d1 和 d2 設的越大，速度就越快。

根據你自己使用的數學函數庫，也許它提供了簡寫。自由需將 e 進行指數計算成為一個普遍的操作，通常會提供一個內建函數一般叫 exp 。比如 Javascript ，你可以直接用 Math.exp(-d1 * t), 這和用 Math.pow(Math.E, -d1 * t) 相同，但更簡短，也許更加高效。

於是我們的虛擬碼可以寫成這樣：

x = A * sin(a * t + p1) * exp(-d1 * t)
y = B * sin(b * t + p2) * exp(-d2 * t)

函數

走起！我們的函數將會是下面這個樣子：

function harmonograph(cx, cy, A, B, a, b, p1, p2, d1, d2, iter) {
  res = 0.01
  t = 0.0
  for (i = 0; t < iter; i += res) {
    x = cx + sin(a * t + p1) * A * exp(-d1 * t)
    y = cy + sin(b * t + p2) * B * exp(-d2 * t)
    lineTo(x, y)
    t += res
  }
  stroke()
}

現在有了一大堆引數。但你應該已經知道了它們中的大部分。我首先要介紹變數 iter. 之前我們迴圈一直是從 0 到 2 * PI 。現在我們期望更多，隨著曲線的持續改變和運動範圍的減小。我們設一個非常大的值給 iter 用於模擬諧振長時間執行。在現實現世中單個諧波圖繪製會花費5分鐘以上。

下面是呼叫：

width = 800
height = 800
canvas(width, height)
 
A = 390
B = 390
a = 2.0
b = 2.01
p1 = 0.3
p2 = 1.7
d1 = 0.001
d2 = 0.001
iter = 100000
 
harmonograph(width / 2, height / 2, A, B, a, b, p1, p2, d1, d2, iter)

是的... 10 萬次迭代。也許會花個 1 到 2 秒，但你應該可以看到類似下面的結果：

（譯者注：注意這個 10 萬次的迭代在我的 firefox 瀏覽器中感覺花了10多秒才畫完，繪製過程瀏覽器會出現假死現象， webkit 核心的瀏覽器上完全顯示不出來，所以需要減小 iter 值）

下面是嘗試使用隨機引數產生的結果：

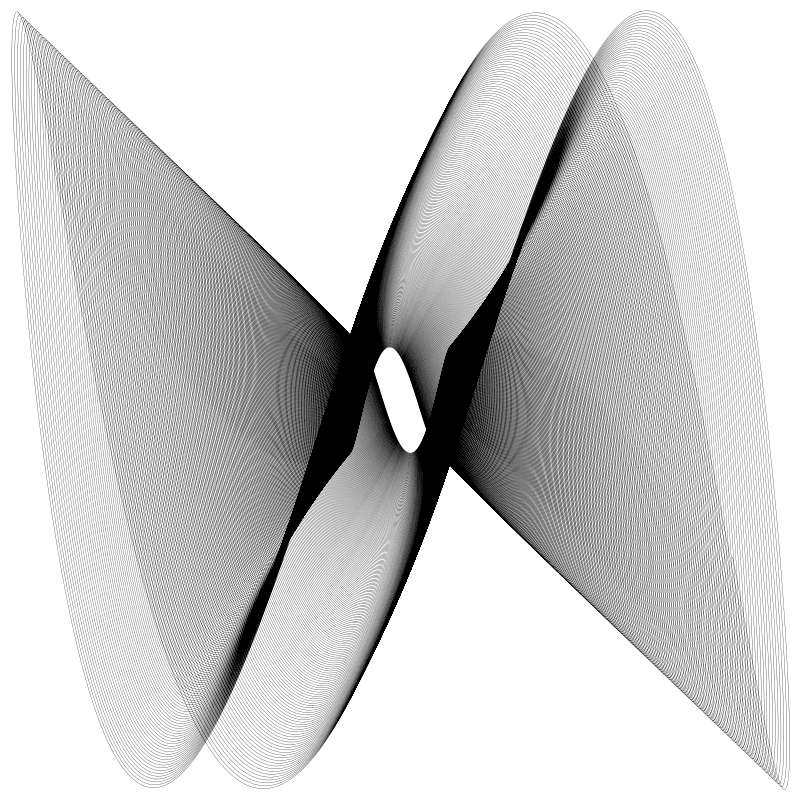
我發現最好將 a 和 b 設為非常相近的值，讓它們變化量很小，比如像最上面的例子我設它們為 2.0 和 2.01。如果將值設為相關的簡單比例值也很好，比如 7.5 和 2.5 它們的比值是 3 : 1。你再將其中的某個值改動一丟丟的量，它將會變的更有趣，比如 7.5 和 2.501。但如果是完全隨機的值如 5.7 和 3.2 這會產生相當狂野的圖形。

d 值決定鐘擺衰減的快慢，所以較小的值將會在距離中心處產生更多的線條。下面是將上面例子中自各衰減值設為 0.0003 後的結果：

這是衰減值設為 0.003 的結果：

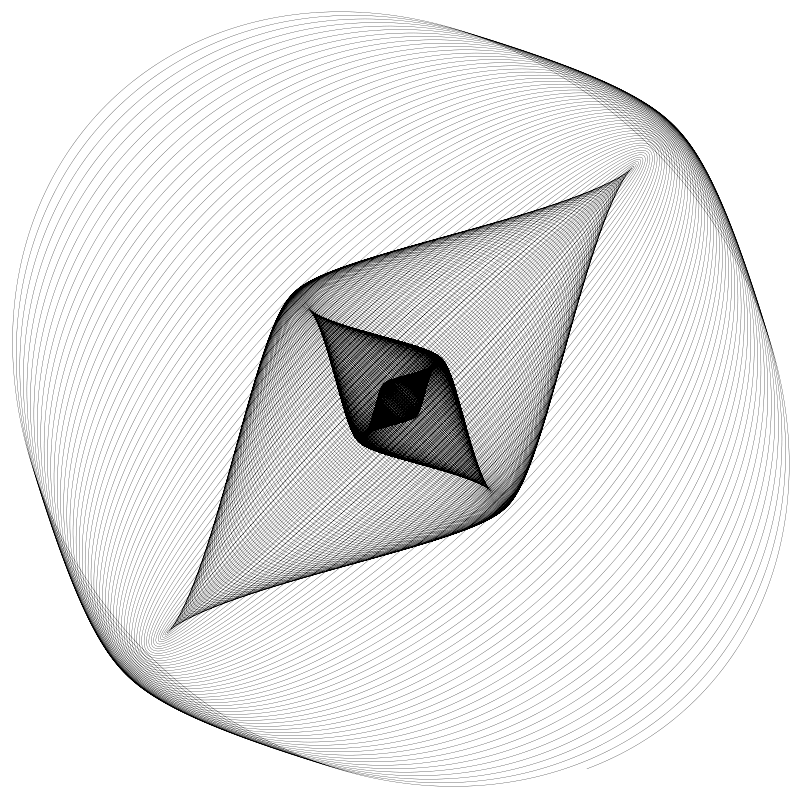
鐘擺衰退的很快且離中心點近的位置畫了更多線條。

你可以好好嘗試一下，比如給它加點顏色!

雙鐘擺

最後一個視訊中繪製產生的圖形非常有吸引力。為了實現它需要實現雙鐘擺模擬。你可以認為我們有一支筆給它 x，y 軸鐘擺，還有另一張紙也擁有 x, y 軸鐘擺。兩者都單獨運動，最終創造出複雜的曲線。你只需要計出各兩個 x 軸的鐘擺值加在一起給 x ，y 軸也同樣做。

儘管概念上相對直白，但意味著我們需要傳雙倍的引數。每個振幅，頻率，相位，衰減都需要傳兩遍。如果我們真這麼傻白甜的做了，它可能會是像下面這樣的程式碼實現那是相當難維護了。

// 別這麼幹 !!!
function harmonograph2(cx, cy, a1, a2, a3, a4, f1, f2, f3, f4, p1, p2, p3, p4, d1, d2, d3, d4, iter) {
  res = 0.01
  t = 0.0
  for (i = 0; t < iter; i += res) {
    x = cx + sin(f1 * t + p1) * a1 * exp(-d1 * t) + sin(f2 * t + p2) * a2 * exp(-d2 * t)
    y = cy + sin(f3 * t + p3) * a3 * exp(-d3 * t)+ sin(f4 * t + p4) * a4 * exp(-d4 * t)
    lineTo(x, y)
    t += res
  }
  stroke()
}

我試過這樣做把我整懵了根本記不住哪個變數控制哪個軸的鐘擺頻率，引數太高不清。更好的做法（可能是不是最好的）是將它們安裝單軸（振幅，頻率，相位，衰減）的鐘擺需求封裝成引數形式到一個物件內，然後傳給函數。

我不知道你使用的平臺語言用的是類或者結構或僅僅是純粹的普通通用物件，所以你只需要知道我們有這樣個擁有4個引數的物件用於傳參：

pendulum: {
  amp,
  freq,
  phase,
  damp,
}

這裡別擔心語法，用你所在平臺的語法實現這樣一個物件即可。

現在我們可以建立四個物件，它們可能命名為 penX，penY，paperX，paperY。像這樣：

penX = pendulum(90.0, 7.5, 1.57, 0.0001)
penY = pendulum(90.0, 4.0, 0.0, 0.0001)
paperX = pendulum(280.0, 1.001, 1.57, 0.0001)
paperY = pendulum(280.0, 2.0, 0.0, 0.0001)

再次提醒，別關心語法。為每個鐘擺週期你需要建立一個工廠函數或一個建構函式或者類似的一個包含振幅，頻率，相位，衰減物件字面量。

現在我們可以將 harmonograph2 函數改成下面這樣：

function harmonograph2(cx, cy, penX, penY, papX, papY, iter) {
  res = 0.01
  t = 0.0
  for (i = 0; t < iter; i += res) {
 
    x = cx
      + sin(penX.freq * t + penX.phase) * penX.amp * exp(-penX.damp * t)
      + sin(papX.freq * t + papX.phase) * papX.amp * exp(-papX.damp * t)
 
    y = cy 
      + sin(penY.freq * t + penY.phase) * penY.amp * exp(-penY.damp * t)
      + sin(papY.freq * t + papY.phase) * papY.amp * exp(-papY.damp * t)
 
    lineTo(x, y)
    t += res
  }
  stroke()
}

這裡仍然有些重複的程式碼，但這是個好的開始。我儘可能保證它的可讀性。你當然可以將它寫的更簡潔，但這常常是在複雜程式設計中有趣的部分先概念驗證再轉為優雅的程式碼實現。我並不想在這上面深入太多。你可以自己去優化。

penX = pendulum(90.0, 7.5, 1.57, 0.0001)
penY = pendulum(90.0, 4.0, 0.0, 0.0001)
paperX = pendulum(280.0, 1.001, 1.57, 0.0001)
paperY = pendulum(280.0, 2.0, 0.0, 0.0001)
 
harmonograph2(width/2, height/2, penX, penY, paperX, paperY, 100000)

如果你做的沒錯（且我上面的程式碼也沒寫錯的）的話，你應該會得到以下這個圖形：

很接近了是不是？引數值並沒用啥魔法。為了讓圖形看起來很酷，我只是隨意改動測試了一下引數值。下面是更多應用別的引數值後的結果：

penX = pendulum(50.0, 17.5, 1.57, 0.0001)
penY = pendulum(50.0, 11.0, 0.5, 0.0001)
paperX = pendulum(280.0, 0.50, 1.57, 0.0007)
paperY = pendulum(280.0, 1.50, 0.0, 0.0007)

你可以多式式，它將產生無窮無盡的圖形。