編碼器

基於 transformer 的編碼器-解碼器模型是 表徵學習 和 模型架構 這兩個領域多年研究成果的結晶。本文簡要介紹了神經編碼器-解碼器模型的歷史，更多背景知識，建議讀者閱讀由 Sebastion Ruder 撰寫的這篇精彩博文。此外，建議讀者對 自注意力 (self-attention) 架構 有一個基本瞭解，可以閱讀 Jay Alammar 的這篇博文複習一下原始 transformer 模型。

本文分 4 個部分:

背景 - 簡要回顧了神經編碼器-解碼器模型的歷史，重點關注基於 RNN 的模型。
編碼器-解碼器 - 闡述基於 transformer 的編碼器-解碼器模型，並闡述如何使用該模型進行推理。
編碼器 - 闡述模型的編碼器部分。
解碼器 - 闡述模型的解碼器部分。

每個部分都建立在前一部分的基礎上，但也可以單獨閱讀。這篇分享是第三部分 編碼器。

如前一節所述， 基於 transformer 的編碼器將輸入序列對映到上下文相關的編碼序列:

\[f_{\theta_{\text{enc}}}: \mathbf{X}_{1:n} \to \mathbf{\overline{X}}_{1:n} \]

仔細觀察架構，基於 transformer 的編碼器由許多 殘差注意力模組 堆疊而成。每個編碼器模組都包含一個雙向自注意力層，其後跟著兩個前饋層。這裡，為簡單起見，我們忽略歸一化層 (normalization layer)。此外，我們不會深入討論兩個前饋層的作用，僅將其視為每個編碼器模組 \({}^1\) 的輸出對映層。雙向自注意層將每個輸入向量 \(\mathbf{x'}_j, \forall j \in {1, \ldots, n}\) 與全部輸入向量 \(\mathbf{x'}_1, \ldots, \mathbf{x'}_n\) 相關聯並通過該機制將每個輸入向量 \(\mathbf{x'}_j\) 提煉為與其自身上下文相關的表徵: \(\mathbf{x''}_j\)。因此，第一個編碼器塊將輸入序列 \(\mathbf{X}_{1:n}\) (如下圖淺綠色所示) 中的每個輸入向量從 上下文無關 的向量表徵轉換為 上下文相關 的向量表徵，後面每一個編碼器模組都會進一步細化這個上下文表徵，直到最後一個編碼器模組輸出最終的上下文相關編碼 \(\mathbf{\overline{X}}_{1:n}\) (如下圖深綠色所示)。

我們對 編碼器如何將輸入序列 "I want to buy a car EOS" 變換為上下文編碼序列這一過程進行一下視覺化。與基於 RNN 的編碼器類似，基於 transformer 的編碼器也在輸入序列最後新增了一個 EOS，以提示模型輸入向量序列已結束 \({}^2\)。

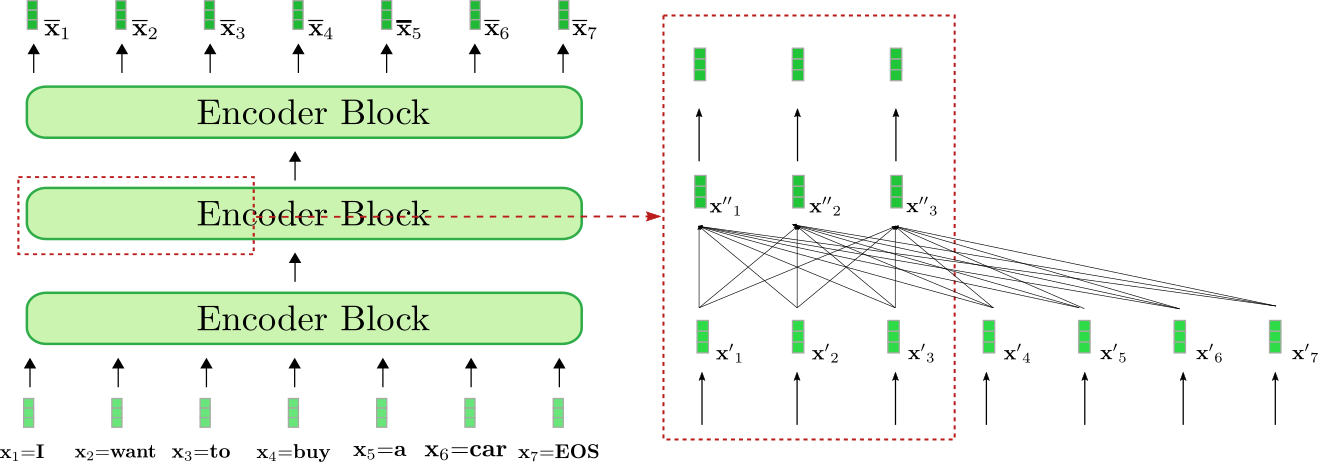
上圖中的 基於 transformer 的編碼器由三個編碼器模組組成。我們在右側的紅框中詳細列出了第二個編碼器模組的前三個輸入向量: \(\mathbf{x}_1\)，\(\mathbf {x}_2\) 及 \(\mathbf{x}_3\)。紅框下部的全連線圖描述了雙向自注意力機制，上面是兩個前饋層。如前所述，我們主要關注雙向自注意力機制。

可以看出，自注意力層的每個輸出向量 \(\mathbf{x''}_i, \forall i \in {1, \ldots, 7}\) 都直接依賴於所有輸入向量 \(\mathbf{x'}_1, \ldots, \mathbf{x'}_7\)。這意味著，單詞「want」的輸入向量表示 \(\mathbf{x'}_2\) 與單詞「buy」 (即 \(\mathbf{x'}_4\)) 和單詞「I」 (即 \(\mathbf{x'}_1\)) 直接相關。因此，「want」的輸出向量表徵，即 \(\mathbf{x''}_2\)，是一個融合了其上下文資訊的更精細的表徵。

我們更深入瞭解一下雙向自注意力的工作原理。編碼器模組的輸入序列 \(\mathbf{X'}_{1:n}\) 中的每個輸入向量 \(\mathbf{x'}_i\) 通過三個可訓練的權重矩陣 \(\mathbf{W}_q\)，\(\mathbf{W}_v\)，\(\mathbf{W}_k\) 分別投影至 key 向量 \(\mathbf{k}_i\)、value 向量 \(\mathbf{v}_i\) 和 query 向量 \(\mathbf{q}_i\) (下圖分別以橙色、藍色和紫色表示):

\[\mathbf{q}_i = \mathbf{W}_q \mathbf{x'}_i, \]

\[\mathbf{v}_i = \mathbf{W}_v \mathbf{x'}_i, \]

\[\mathbf{k}_i = \mathbf{W}_k \mathbf{x'}_i, \]

\[\forall i \in {1, \ldots n } \]

請注意，對每個輸入向量 \(\mathbf{x}_i (\forall i \in {i, \ldots, n}\)) 而言，其所使用的權重矩陣都是相同的。將每個輸入向量 \(\mathbf{x}_i\) 投影到 query 、 key 和 value 向量後，將每個 query 向量 \(\mathbf{q}_j (\forall j \in {1, \ldots, n}\)) 與所有 key 向量 \(\mathbf{k}_1, \ldots, \mathbf{k}_n\) 進行比較。哪個 key 向量與 query 向量 \(\mathbf{q}_j\) 越相似，其對應的 value 向量 \(\mathbf{v}_j\) 對輸出向量 \(\mathbf{x''}_j\) 的影響就越重要。更具體地說，輸出向量 \(\mathbf{x''}_j\) 被定義為所有 value 向量的加權和 \(\mathbf{v}_1, \ldots, \mathbf{v}_n\) 加上輸入向量 \(\mathbf{x'}_j\)。而各 value 向量的權重與 \(\mathbf{q}_j\) 和各個 key 向量 \(\mathbf{k}_1, \ldots, \mathbf{k}_n\) 之間的餘弦相似度成正比，其數學公式為 \(\textbf{Softmax}(\mathbf{K}_{1:n}^\intercal \mathbf{q}_j)\)，如下文的公式所示。關於自注意力層的完整描述，建議讀者閱讀這篇博文或原始論文。

好吧，又複雜起來了。我們以上例中的一個 query 向量為例圖解一下雙向自注意層。為簡單起見，本例中假設我們的 基於 transformer 的解碼器只有一個注意力頭 config.num_heads = 1 並且沒有歸一化層。

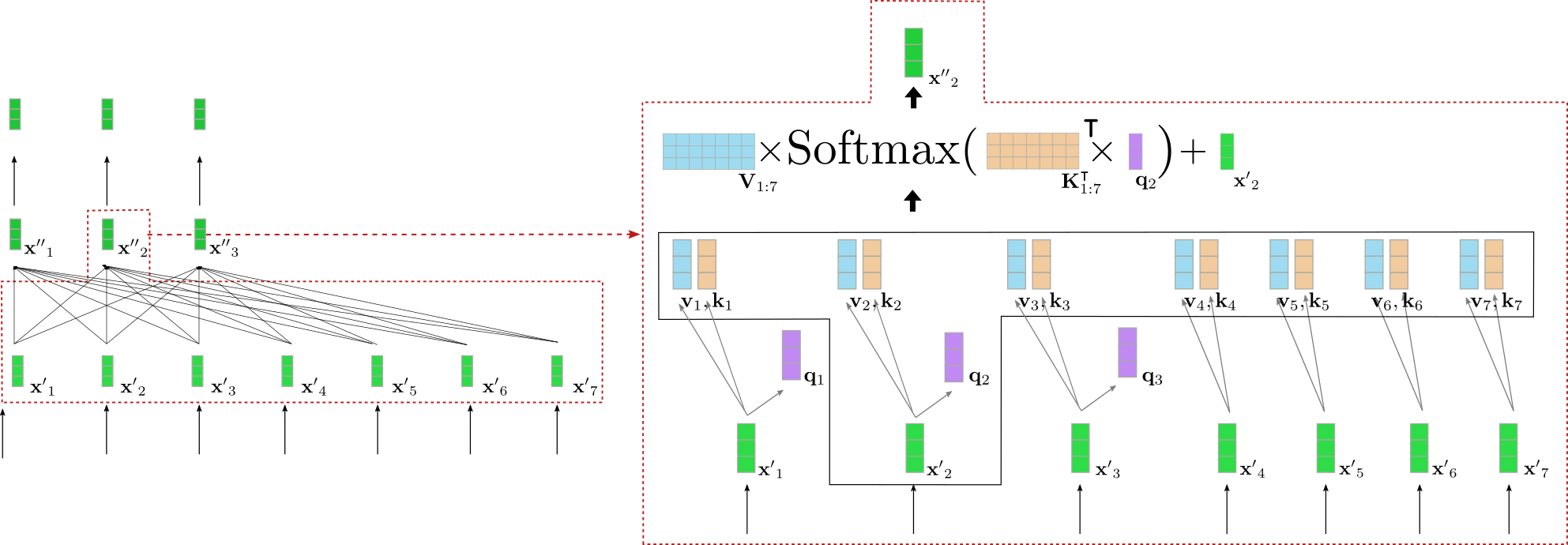
圖左顯示了上個例子中的第二個編碼器模組，右邊詳細視覺化了第二個輸入向量 \(\mathbf{x'}_2\) 的雙向自注意機制，其對應輸入詞為「want」。首先將所有輸入向量 \(\mathbf{x'}_1, \ldots, \mathbf{x'}_7\) 投影到它們各自的 query 向量 \(\mathbf{q}_1, \ldots, \mathbf{q}_7\) (上圖中僅以紫色顯示前三個 query 向量)， value 向量 \(\mathbf{v}_1, \ldots, \mathbf{v}_7\) (藍色) 和 key 向量 \(\mathbf{k}_1, \ldots, \mathbf{k}_7\) (橙色)。然後，將 query 向量 \(\mathbf{q}_2\) 與所有 key 向量的轉置 ( 即 \(\mathbf{K}_{1:7}^{\intercal}\)) 相乘，隨後進行 softmax 操作以產生 自注意力權重 。自注意力權重最終與各自的 value 向量相乘，並加上輸入向量 \(\mathbf{x'}_2\)，最終輸出單詞「want」的上下文相關表徵，即 \(\mathbf{x''}_2\) (圖右深綠色表示)。整個等式顯示在圖右框的上部。 \(\mathbf{K}_{1:7}^{\intercal}\) 和 \(\mathbf{q}_2\) 的相乘使得將「want」的向量表徵與所有其他輸入 (「I」，「to」，「buy」，「a」，「car」，「EOS」) 的向量表徵相比較成為可能，因此自注意力權重反映出每個輸入向量 \(\mathbf{x'}_j\) 對「want」一詞的最終表徵 \(\mathbf{x''}_2\) 的重要程度。

為了進一步理解雙向自注意力層的含義，我們假設以下句子: 「 房子很漂亮且位於市中心，因此那兒公共交通很方便 」。「那兒」這個詞指的是「房子」，這兩個詞相隔 12 個字。在基於 transformer 的編碼器中，雙向自注意力層運算一次，即可將「房子」的輸入向量與「那兒」的輸入向量相關聯。相比之下，在基於 RNN 的編碼器中，相距 12 個字的詞將需要至少 12 個時間步的運算，這意味著在基於 RNN 的編碼器中所需數學運算與距離呈線性關係。這使得基於 RNN 的編碼器更難對長程上下文表徵進行建模。此外，很明顯，基於 transformer 的編碼器比基於 RNN 的編碼器-解碼器模型更不容易丟失重要資訊，因為編碼的序列長度相對輸入序列長度保持不變，即 \(\textbf{len }(\mathbf{X}_{1:n}) = \textbf{len}(\mathbf{\overline{X}}_{1:n}) = n\)，而 RNN 則會將 \(\textbf{len}((\mathbf{X}_{1:n}) = n\) 壓縮到 \(\textbf{len}(\mathbf{c}) = 1\)，這使得 RNN 很難有效地對輸入詞之間的長程依賴關係進行編碼。

除了更容易學到長程依賴外，我們還可以看到 transformer 架構能夠並行處理文字。從數學上講，這是通過將自注意力機制表示為 query 、 key 和 value 的矩陣乘來完成的:

\[\mathbf{X''}_{1:n} = \mathbf{V}_{1:n} \text{Softmax}(\mathbf{Q}_{1:n}^\intercal \mathbf{K}_{1:n}) + \mathbf{X'}_{1:n} \]

輸出 \(\mathbf{X''}_{1:n} = \mathbf{x''}_1, \ldots, \mathbf{x''}_n\) 是由一系列矩陣乘計算和 softmax 操作算得，因此可以有效地並行化。請注意，在基於 RNN 的編碼器模型中，隱含狀態 \(\mathbf{c}\) 的計算必須按順序進行: 先計算第一個輸入向量的隱含狀態 \(\mathbf{x}_1\); 然後計算第二個輸入向量的隱含狀態，其取決於第一個隱含向量的狀態，依此類推。RNN 的順序性阻礙了有效的並行化，並使其在現代 GPU 硬體上比基於 transformer 的編碼器模型的效率低得多。

太好了，現在我們應該對:
a) 基於 transformer 的編碼器模型如何有效地建模長程上下文表徵，以及
b) 它們如何有效地處理長序列向量輸入這兩個方面有了比較好的理解了。

現在，我們寫一個 MarianMT 編碼器-解碼器模型的編碼器部分的小例子，以驗證這些理論在實踐中行不行得通。

\({}^1\) 關於前饋層在基於 transformer 的模型中所扮演的角色的詳細解釋超出了本文的範疇。Yun 等人 (2017) 的工作認為前饋層對於將每個上下文向量 \(\mathbf{x'}_i\) 對映到目標輸出空間至關重要，而單靠 自注意力 層無法達成這一目的。這裡請注意，每個輸出詞元 \(\mathbf{x'}\) 都經由相同的前饋層處理。更多詳細資訊，建議讀者閱讀論文。

\({}^2\) 我們無須將 EOS 附加到輸入序列，雖然有工作表明，在很多情況下加入它可以提高效能。相反地，基於 transformer 的解碼器必須把 \(\text{BOS}\) 作為第 0 個目標向量，並以之為條件預測第 1 個目標向量。

from transformers import MarianMTModel, MarianTokenizer
import torch

tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")

embeddings = model.get_input_embeddings()

# create ids of encoded input vectors
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids

# pass input_ids to encoder
encoder_hidden_states = model.base_model.encoder(input_ids, return_dict=True).last_hidden_state

# change the input slightly and pass to encoder
input_ids_perturbed = tokenizer("I want to buy a house", return_tensors="pt").input_ids
encoder_hidden_states_perturbed = model.base_model.encoder(input_ids_perturbed, return_dict=True).last_hidden_state

# compare shape and encoding of first vector
print(f"Length of input embeddings {embeddings(input_ids).shape[1]}. Length of encoder_hidden_states {encoder_hidden_states.shape[1]}")

# compare values of word embedding of "I" for input_ids and perturbed input_ids
print("Is encoding for `I` equal to its perturbed version?: ", torch.allclose(encoder_hidden_states[0, 0], encoder_hidden_states_perturbed[0, 0], atol=1e-3))

輸出:

    Length of input embeddings 7. Length of encoder_hidden_states 7
    Is encoding for `I` equal to its perturbed version?: False

我們比較一下輸入詞嵌入的序列長度 ( 即 embeddings(input_ids)，對應於 \(\mathbf{X}_{1:n}\)) 和 encoder_hidden_states 的長度 (對應於\(\mathbf{\overline{X}}_{1:n}\))。同時，我們讓編碼器對單詞序列「I want to buy a car」及其輕微改動版「I want to buy a house」分別執行前向操作，以檢查第一個詞「I」的輸出編碼在更改輸入序列的最後一個單詞後是否會有所不同。

不出意外，輸入詞嵌入和編碼器輸出編碼的長度，即 \(\textbf{len}(\mathbf{X}_{1:n})\) 和 \(\textbf{len }(\mathbf{\overline{X}}_{1:n})\)，是相等的。同時，可以注意到當最後一個單詞從「car」改成「house」後，\(\mathbf{\overline{x}}_1 = \text{「I」}\) 的編碼輸出向量的值也改變了。因為我們現在已經理解了雙向自注意力機制，這就不足為奇了。

順帶一提， 自編碼 模型 (如 BERT) 的架構與 基於 transformer 的編碼器模型是完全一樣的。 自編碼 模型利用這種架構對開放域文字資料進行大規模自監督預訓練，以便它們可以將任何單詞序列對映到深度雙向表徵。在 Devlin 等 (2018) 的工作中，作者展示了一個預訓練 BERT 模型，其頂部有一個任務相關的分類層，可以在 11 個 NLP 任務上獲得 SOTA 結果。你可以從此處找到