第四章利薩茹曲線（Lissajous Curves）

原作：Keith Peters https://www.bit-101.com/blog/2022/11/coding-curves/

譯者：池中物王二狗(sheldon)

blog: http://cnblogs.com/willian/

原始碼：github: https://github.com/willian12345/coding-curves

曲線藝術程式設計系列第四章

確保您已知曉了最初一章中我們對範例程式碼的約定。

利薩茹曲線一直以來是我最喜歡的技術之一。除了迴圈的形狀，實際上它可比看起來有用。

在這一篇中我們將覆蓋它的基礎知識，除此之外像往常一樣，我們另外還得看看它在其它方面的應用。

基礎

利薩茹曲線又名利薩茹圖形或鮑迪奇曲線。兩個名字都來自於 19 世紀研究和撰寫它們的人名。

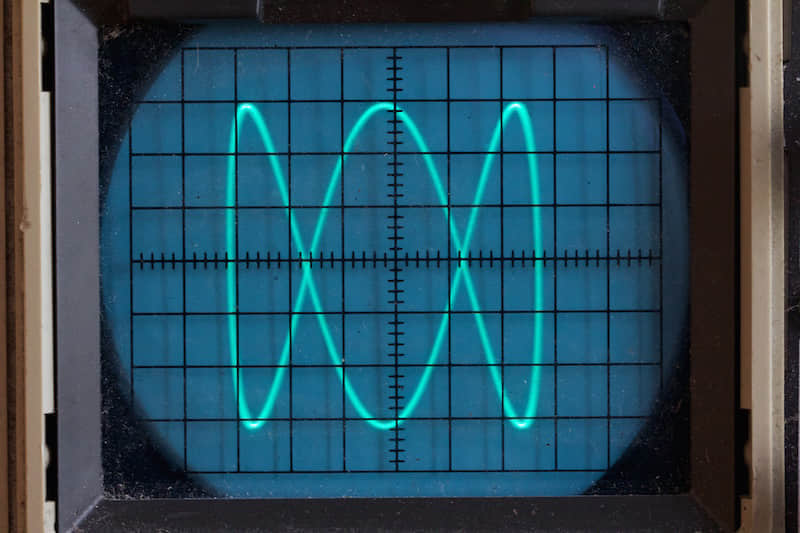
這些曲線圖形由上下左右來回擺動迴圈的長曲線形成。在它們在純粹的形狀時（譯者注：沒有複雜多餘線條時），讓我們想起常常在老式科幻電影中顯示在示波器上發光的圖形。

公式

此番，在一開始我搜尋利薩茹曲線相關題材時就找到了一個有用的引數方程。

x = A * sin(a * t + d)
y = B * sin(b * t)

有一個正弦波在 x 軸，另一個正弦波在 y 軸。它們不會在某個方向上趨向無限，它在週期內自迴圈。

公式中變數挺多的。讓我們分別看看。

A 和 B 最後影響的是曲線在 x 軸寬和 y 軸高。確切的講，只是寬高的一半，因為會在它各自方向上延展。

t 是一個範圍在 0 到 2 * PI 的範圍引數變數。儘管在真正執行時它在各自方向上會超出範圍，但很快它就會返回回來。在 x 方程式中 t 乘以 a, y 方程式中 t 乘以 b ，然後在各自軸結果傳入正弦函數。另外，在 x 方程式中引數 d 或者說 delta 變數用於把它移出相位。

此方程可能看起來像之前章節中我們接觸的圓方程。如果我們將 A 和 B 設為相等並且把它當作 r ，並且將 a 和 b 設為 1，再去掉 d ,再用餘弦代替 x 方程的正弦函數，我們就得到了：

x = r * cos(t)
y = r * sin(t)

這就是原點在 0，0 的圓方程了。因為餘弦就是正弦 +90 度，所以我們也可以說：

x = r * sin(t + d)
y = r * sin(t)

... 這個 d 就是 90 度，或者 PI / 2 弧度。

A 和 B 分開的情況你在橢圓方程裡已經見過了，在那裡 A 我們叫作 '半徑 x', B 就是「半徑 y」

x = A * sin(t + d)
y = B * sin(t)

所以當引數像上面那樣同步變化，我們得到的是圓或橢圓，但當我們改動一些引數後，我們將得到了更有趣的曲線。

好了，說的夠多了，開始編碼吧。我們直接跳到建立一個利薩如函數。我會簡化一下。

function liss(cx, cy, A, B, a, b, d) {
  res = 0.01
  for (t = 0; t < 2 * PI; t += res) {
    x = cx + sin(a * t + d) * A
    y = cy + sin(b * t) * B
    lineTo(x, y)
  }
  closePath()
}

此處，解析度變數 res 值不像之前在圓和橢圓函數內那樣。在這裡我給了一個很小的值，儘管它意味著畫更多簡單的小曲線。這樣設定後從 0 到 2 * PI (6.28...), 從 0.01 開始增長將會得到 528 條線段，這對大多數例子來說足夠用了（譯者注：線段越多意味著越平滑）。如果曲線變的不平滑了，你就改這個值讓線段變的更多。但我不打算深入測算到一個合適的值。

現在我們能用它畫出來像下面這樣呼叫：

width = 600
height = 600
canvas(600, 600)
 
liss(300, 300, 250, 250, 1, 1, PI / 2)
stroke()

這個圖就像我上面說的那樣，我把 A 和 B 設為相等的值，a 和 b 設為 1 並且 d 設為 PI / 2 。這樣實際得到的結果就是一個圓形...

... 看，確實是圓。

讓我們先將 d 設為 0 然後 a 和 b 稍後小變化一下子。這裡，將 a 和 b 分別設定為 2 和 1（再次 d 設為 0）

liss(300, 300, 250, 250, 2, 1, 0)

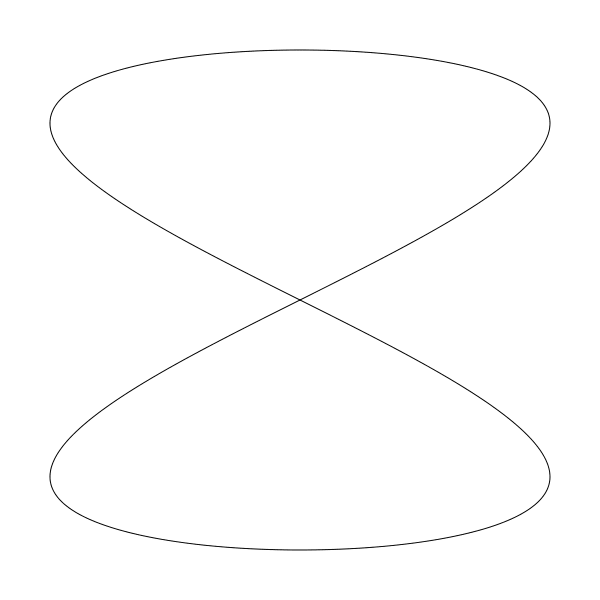
設為 2 和 3 時：

liss(300, 300, 250, 250, 2, 3, 0)

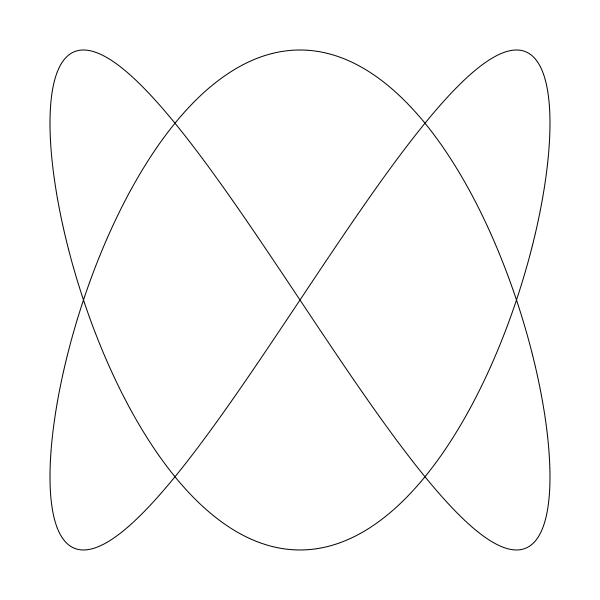
讓我們調的更大一點，11 和 8

liss(300, 300, 250, 250, 11, 8, 0)

以上的這幾個例子都中 d 都是 0，波形都在自己軸的相位。現在我們保持 11 和 8 不變，將 d 變成 0.5，移出它們的相位。

liss(300, 300, 250, 250, 11, 8, 0.5)

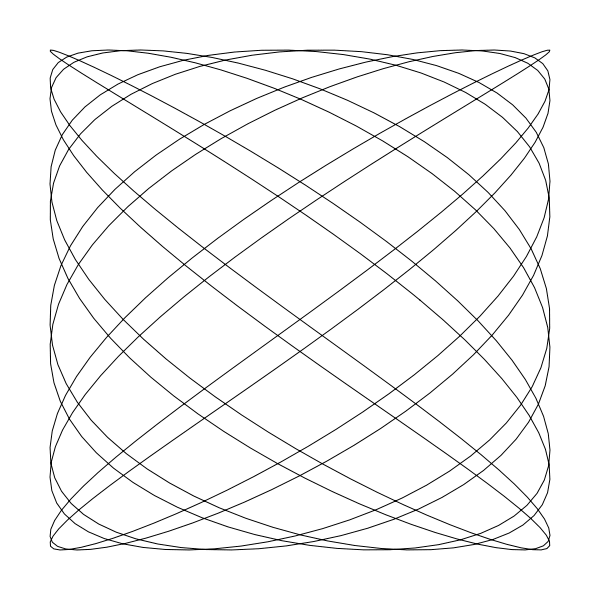
這裡的動畫是 a 為 6，b 為 7， d 持續變化時產生的圖形變化

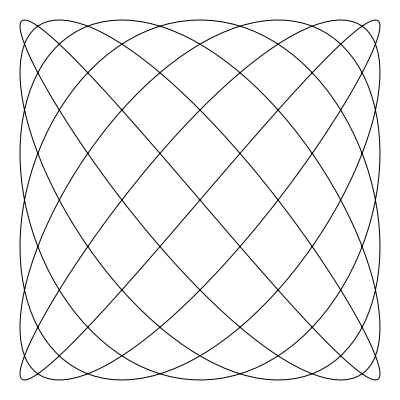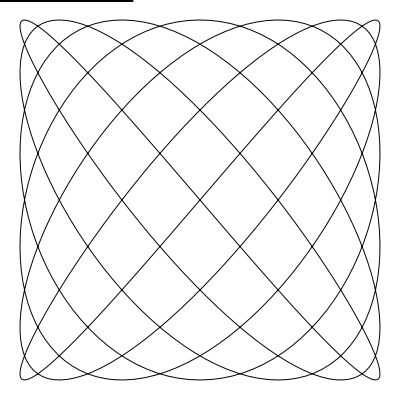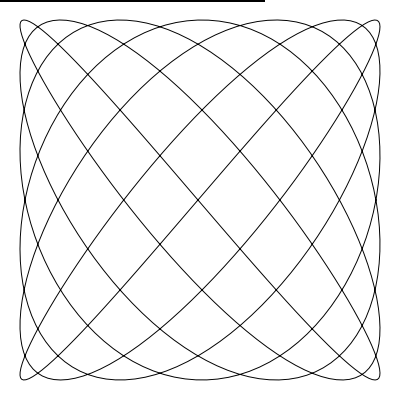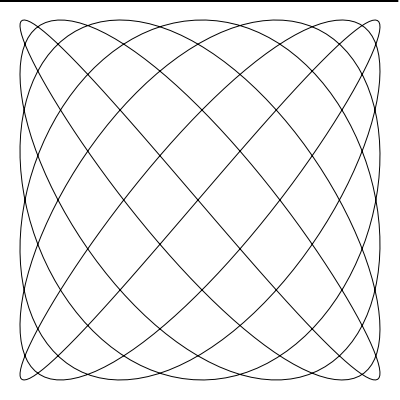
如果你希望你建立的曲線首尾絲滑的連線，那麼沒有什麼比 a 和 b 不是整數更糟的了（譯者注：想絲滑需要 a 和 b 為整數）。如果你將 a 設為 6.4，b 設為 7.3

liss(300, 300, 250, 250, 6.4, 7.3, 0)

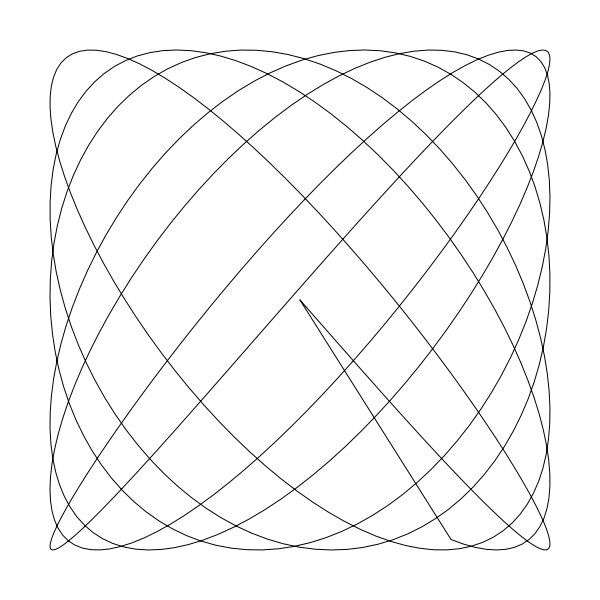
如果你想看清楚點發生了啥，那麼將 closePath 從函數內註釋掉看看結果：

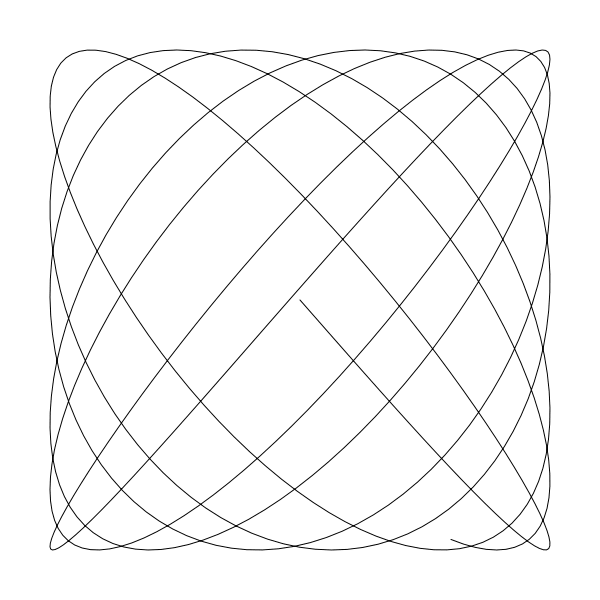
現在你可以看到曲線開始與結束點在隨機位置，而不是像 a 與 b 為整數時絲滑的連線起來。

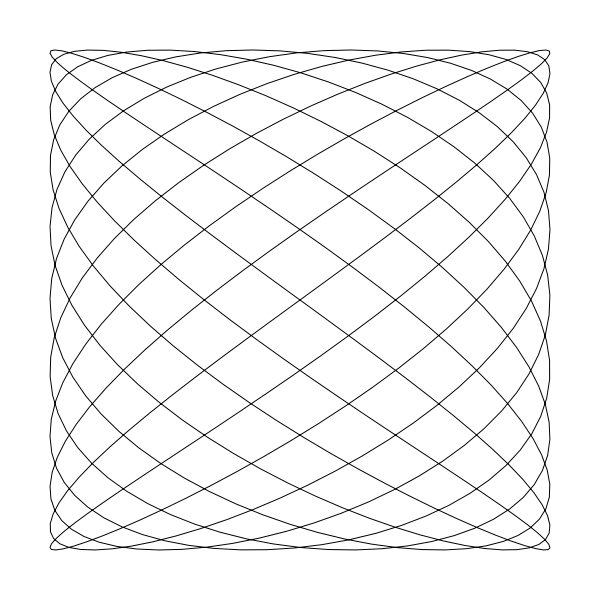
當然，當你在這裡使用小數時，你可以將變數 t 的範圍從 0 到 2 * PI 繼續放大到可以填滿整個空間。這裡是我將 t 範圍擴充套件到 20 * PI 的效果：

如果 a 和 b 你使用了有理數路徑將最終又連線起來。但可能會花點時間（譯者注：如果是在動畫中）。這個圖中看起來就基本很接近了。

我們當然也能通過改變 A 和 B 這兩個變數來獲取寬的圖形：

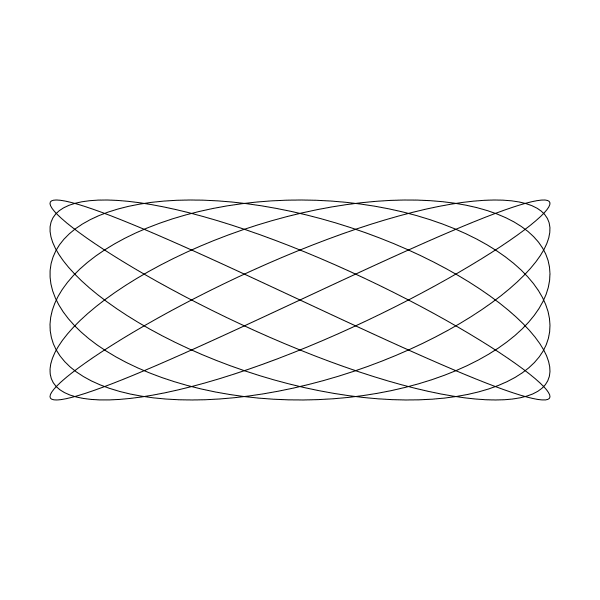
A = 250, B = 100

or tall figures:

或高的

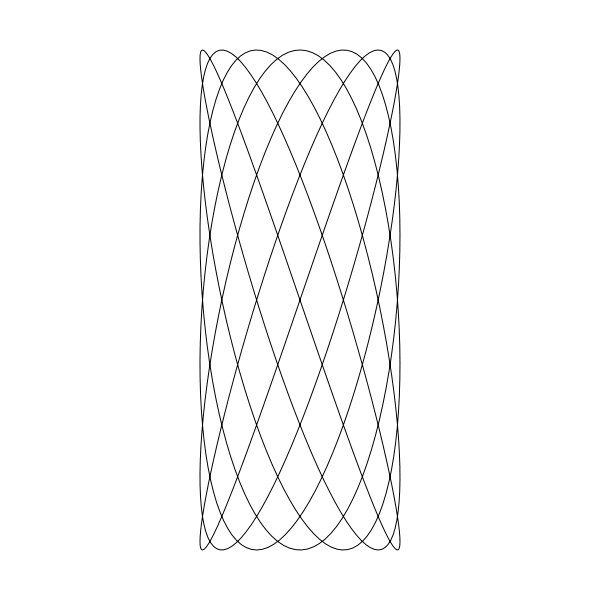
A = 100, B = 250

這就是繪製利薩茹圖形最直接的方法。可以查查維基百科與此相關的資料，學習一下這類曲線的多種屬性。我考慮在這裡建立一個可互動的 demo，但最後發現網上已經有很多了。文章最後我放了一些連結

取而代之的是，我們可以看看另外的應用方向。

動畫

此處不會像上面做的曲線動畫一樣，不討論曲線自身的動畫，但會利用利薩茹曲線的結果應用在某個物件上。

但，首先我們先聊一聊最基礎的動畫

擺動(振盪)

通常你想在螢幕上對一個物件進行動畫但又不想它超出螢幕，讓它上下左右的動，或者對它進行扭曲，變大，縮小。你可能已經學習過一些 2D 圖形變形屬性，平移，旋轉，縮放。你可以用正弦或餘弦函數計算結果值應用於這些變形屬性，隨著時間的推移改變那些函數方法的輸入值就可以。

我們需要擴充套件一下我們的虛擬碼，它包含一個 loop 迴圈函數用於時刻進行不同繪製，它執行起來就是動畫了。Processing （譯者注：一個著名的圖形庫）已經有內建的功能，其它圖形系統也有類似的功能。但是你可能需要自己編寫一個函數來實現這些功能。如果你用的是 HTML 和 javascript 的，那麼我們可以使用 requestAnimationFrame 函數來實現。

我們假定它也擁有一個 clearCanvas 方法。我們可以把上一篇中編寫的 circle 函數用到此處，或者使用你編碼平臺內建的繪圖 api 。我們像下面這樣開始：

width = 400
height = 400
t = 0
canvas(width, height)
 
function loop() {
  clearScreen()
  circle(width / 2 + sin(t) * 100, height / 2, 20)
  fill()
  t += 0.1
}

這裡將正弦中的 t 乘以 100 以獲得圓在 x 軸上的偏移。當 t 持續增長時，這個圓會來回運動。你也可以簡單的對 y 軸應用同樣的效果。或者應用在半徑上：

width = 400
height = 400
t = 0
canvas(width, height)
 
function loop() {
  clearScreen()
  circle(width / 2, height / 2, 50 + sin(t) * 20)
  fill()
  t += 0.1
}

此處，我們用 50 作為基礎半徑，加上使用 t 的正弦值乘以 20。由於正弦值從 -1 到 +1 ，半徑會加上 -20 到 +20 , 結果就是 30 至 70 之間擺動。

我們同樣也可以將此應用在旋轉屬性上，但需要換一下圖形，以便於我們可以觀察到它的旋轉。我把這個留給你自己實現吧。

回到繞圓運動。我們希望它繞整個 canvas 做圓周執行。我們一樣可以使用正弦配合餘弦完成圓周運動：

width = 400
height = 400
t = 0
canvas(width, height)
 
function loop() {
  clearScreen()
  circle(width / 2 + cos(t) * 100, height / 2 + sin(t) * 100, 20)
  fill()
  t += 0.1
}

假設我們希望它運動的更加自然該如何實現？我們可以為它新增一些隨機運動，然後你會發現一個問題，如何保證它只在螢幕內運動。不難，我們可以使用利薩茹的公式來實現這一點，像下面這樣：

width = 400
height = 400
t = 0
a = 13
b = 11
canvas(width, height)
 
function loop() {
  clearScreen()
  circle(width / 2 + sin(a * t) * 100, height / 2 + sin(b * t) * 100, 20)
  fill()
  t += 0.02
}

雖然這是一個不太完美的迴圈運動 gif 動畫，但精神你肯定已經領會到了。這個圓看起來就像是隨機繞著螢幕運動，但它實際是按利薩茹曲線路徑運動。在我看來它就像是一隻蒼蠅在來回飛。事實上如果你多新增一些應用不同的引數的圓，那麼它們會看起來更像一群蒼蠅在飛。沒有公分母的 a 和 b 數值設的越高，它在路徑的運動看起來會更加隨機。