技術文章 » 超詳細の樹狀陣列講解！

超詳細の樹狀陣列講解！

2023-06-03 06:00:47

樹狀陣列

以下有錯誤的話歡迎指正

由於篇幅問題每道題目的程式碼在每一板塊最後摺疊給出

其實線段樹能維護的東西比樹狀陣列能維護的東西多得多，但是樹狀陣列程式碼好寫啊！

一維樹狀陣列

最為常用的樹狀陣列，我們一般都是用這個來解決問題，二維的後面會講。

引入

我們在進行數列操作的時候，經常會遇到帶有區間修改的一類問題，比如給定一個數列，支援區間加單點查詢，或者支援區間查詢單點修改之類的。

給定一個序列，需要支援單點修改和區間加，設元素個數為 \(n\)，操作次數為 \(m\)，那麼我們最樸素的暴力的複雜度最壞情況是 \(O(nm)\) 的，顯然只要資料範圍稍微大一點暴力就會掛，這個時候我們就需要用一些資料結構來進行優化，比如線段樹或者我們接下來要講的樹狀陣列。

介紹

首先要學會樹狀陣列，我們就要先理解一個函數：lowbit 函數。

lowbit 函數的返回值就是由當前數轉為二進位制後最低位的 \(1\) 與後面的零所構成的數值，比如一個二進位制數 \(1010100\)，他的 lowbit 值就是 \(lowbit(1010100)=100\)，轉為十進位制也就是 \(lowbit(84)=4\)。

我們如何能求出這個 lowbit 函數的值呢？

  • 暴力，每次模 \(2\)，但顯然複雜度為 \(O(\log x)\)，由於有更快速便捷的方法，我們不能接受多一隻 \(\log\) 的複雜度。

  • 我們考慮到是在二進位制下，那我們就可以用快速的位運算來解決這個問題，我們先把原數如 \(1010100\) 進行取反，得到：\(0101011\)，這個時候，我們再給取反後的數位加上 \(1\)，這個時候，你會發現，得到的數為 \(0101100\)，這個數值和一開始的數的關係，就是除了最後一位 \(1\) 和後面的 \(0\)，其他位都是不同的！所以我們將這兩個一 & 就得到了我們的 lowbit ，也就是 \(lowbit(x)=x\&(\sim x+1)\)。

  • 我們想到計算機中對於負數的儲存用的是二補數，也就是如果一個數是正數，他的二補數就是他本身，如果是負數，那麼他的二補數就是他的反碼然後加一。根據這個特性，我們知道 \(-1010100\) 的反碼為 \(0101011\) 那麼二補數就是 \(0101100\)，這樣再和 \(1010100\) & 一下不就也得到了 lowbit 嗎，也就是 \(lowbit(x)=x\&-x\)。

於是我們轉化成程式碼就是：

inline int lowbit(int x){return x&-x;}

這個有什麼用，我們後面講到操作就知道了。

樹狀陣列是長這個樣子的：

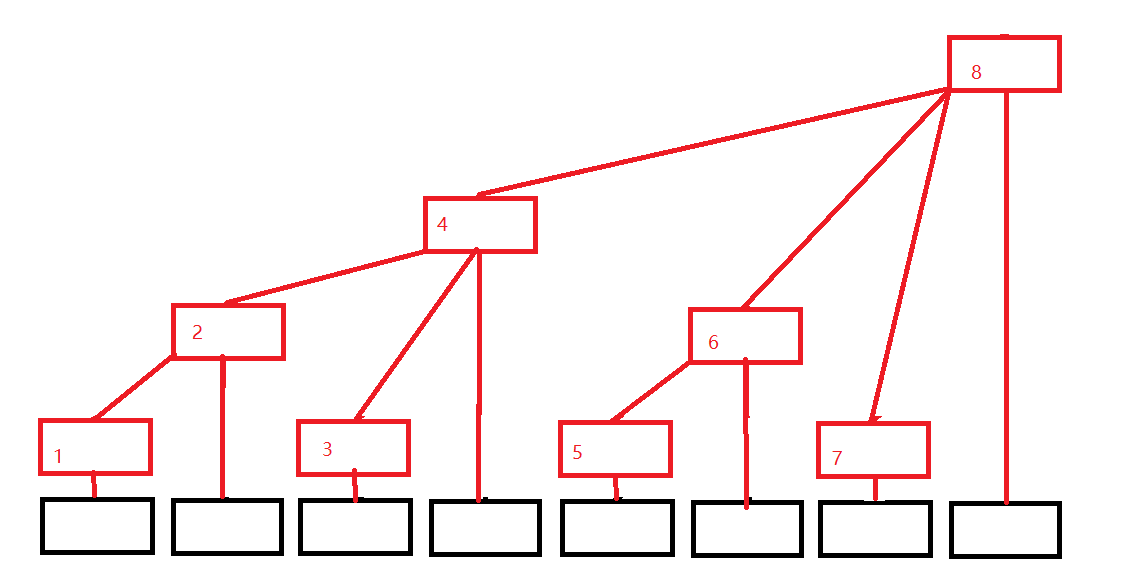
感謝樹狀陣列詳解 - Xenny - 部落格園的圖片。

其中黑色的塊是原來的陣列下面會用 \(a[i]\) 表示，紅色的是樹狀陣列下面會用 \(s[i]\) 來表示。

樹狀陣列的每一個塊，存放的是子節點的和。

用十進位制可以不是很好結合前面的 lowbit ，所以下面的下標我用的是二進位制。

我們可以形象的看作每個節點 \(x\) 所存的是以當前編號 \(x\) 的節點為起點，向左 \(lowbit(x)\) 個單位的所有點的總和。

單點修改區間查詢

也就是這道題目：【模板】樹狀陣列 1 - 洛谷

我們現在來考慮如何單點修改，假設我們要修改裡面的 \(3\) 號點。

我們發現，由於有一些節點是包含 \(3\) 的值的，所以我們也要更新那些值，也就是同時更新 \(3,4,8\) 號節點，我們轉成二進位制看一下：\(11,100,1000\)。

不知道你發現了什麼沒有。

可以看出，下一個修改的節點的編號，就是當前的數 \(x\)，與當前數的 lowbit 值的和！

所以我們對於一次修改操作，可以寫出以下的程式碼：

inline void add(int x,int k){while(x<=n)t[x]+=k,x+=lowbit(x);}

好神奇！

然後我們再來看區間求和的操作。

我們的樹狀陣列維護的就是字首和，所以我們在查詢的時候肯定不能一個一個遍歷，舉個例子，假設我們需要查詢前 \(7\) 個數的和。

我們發現我們實際上需要查詢的有 \(7,6,4\) 號節點。

我們再轉成二進位制看看：\(111,110,100\)

這次的很明顯了吧！

我們發現，下一個需要修改的節點，就是當前 \(x\) 的值減去 \(lowbit(x)\)，所以，我們就又可以寫出以下的程式碼：

inline int ask(int x){int o=0;while(x>=1)o+=t[x],x-=lb(x);return o;}

對於區間查詢，我們利用字首和的思想，設需要查詢的區間為 \([l,r]\)，我們則可以直接輸出 \(ask(r)-ask(l-1)\)。

至此我們就完成了支援區間查詢和單點修改的操作。

區間查詢和單點修改的複雜度最壞均為 \(O(\log n)\)，所以總複雜度為 \(O(m\log n)\)。

完整程式碼：

樹狀陣列單點修改區間查詢 
#include<bits/stdc++.h>
#define int long long
#define N 1001000
using namespace std;
int n,m,t[N];
inline int lb(int x){return x&-x;}
inline void add(int x,int k){while(x<=n)t[x]+=k,x+=lb(x);}
inline int sum(int x){int ans=0;while(x>=1)ans+=t[x],x-=lb(x);return ans;}
signed main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++){int a;cin>>a;add(i,a);}
	for(int i=1;i<=m;i++)
	{
		int op,x,y;
		cin>>op>>x>>y;
		if(op==1)add(x,y);
		if(op==2)cout<<(sum(y)-sum(x-1))<<endl;
	}
	return 0;
}

區間修改單點查詢

【模板】樹狀陣列 2 - 洛谷

我們想一想，什麼東西做區間修改最快？

那當然是差分！直接 \(O(1)\) 修改！但是有一個致命的缺點：查詢第 \(x\) 個數的值的複雜度為 \(O(x)\)，也就是說，最壞複雜度為 \(O(mn)\)，我們怎麼能接受這麼高的複雜度！

那我們用樹狀陣列維護這個差分陣列不就好了？

我們單點查詢變成了之前的查詢前 \(x\) 個數的和，然後我們的區間修改，利用差分的思想，直接修改 \(add(l,k),add(r+1,-k)\) 就好了。

完整 code：

樹狀陣列區間修改單點查詢 
#include<bits/stdc++.h>
#define int long long
#define N 1000100
using namespace std;
int n,m,a[N],t[N];
inline int lb(int x){return x&-x;}
inline void add(int x,int k){while(x<=n)t[x]+=k,x+=lb(x);}
inline int ask(int x){int ans=0;while(x>=1)ans+=t[x],x-=lb(x);return ans;}
signed main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=1;i<=m;i++)
	{
		int op,x,y,k;
		cin>>op;
		if(op==1)
		{
			cin>>x>>y>>k;
			add(x,k);
			add(y+1,-k);
		}
		if(op==2)
		{
			cin>>x;
			int ans=ask(x)+a[x];
			cout<<ans<<endl;
		}
	}
	return 0;
}

區間查詢區間修改

【模板】線段樹 1 - 洛谷

線段樹的模板的操作就是區間查詢和區間修改，但線段樹碼量比較大，所以我們還可以用樹狀陣列來解決。

我們如果想要完成這個操作的話，還是需要用到上面的差分的思想。

首先我們和上面一樣，用差分的話，我們就可以做到 \(O(\log n)\) 的修改，但是，我們對於區間查詢，似乎沒有什麼好辦法。

我們假設要查詢前 \(5\) 個數的和：

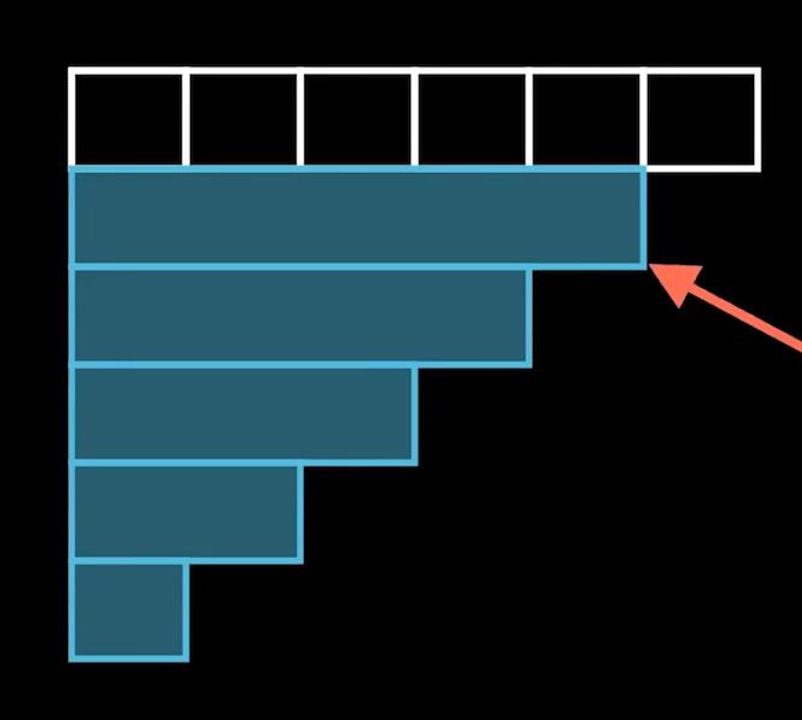
圖片來源：# 完全理解並深入應用樹狀陣列 | 支援多種動態維護區間操作

圖中的藍色陰影部分就是我們要求的值，用 \(S[i]\) 表示我們第 \(i\) 個數的值，\(t1[j]\) 表示當前維護的差分陣列，很容易可以列出式子：

\[S[i]=\sum_{j=1}^{i}t1[j] \]

然後在把 \(1\sim x\) 的數都給加起來：

\[sum=\sum_{i=1}^{x}S[i]=\sum_{i=1}^{x}\sum_{j=1}^{i}t1[j] \]

我們發現這個式子一點也不好算，所以我們轉換一下思路：

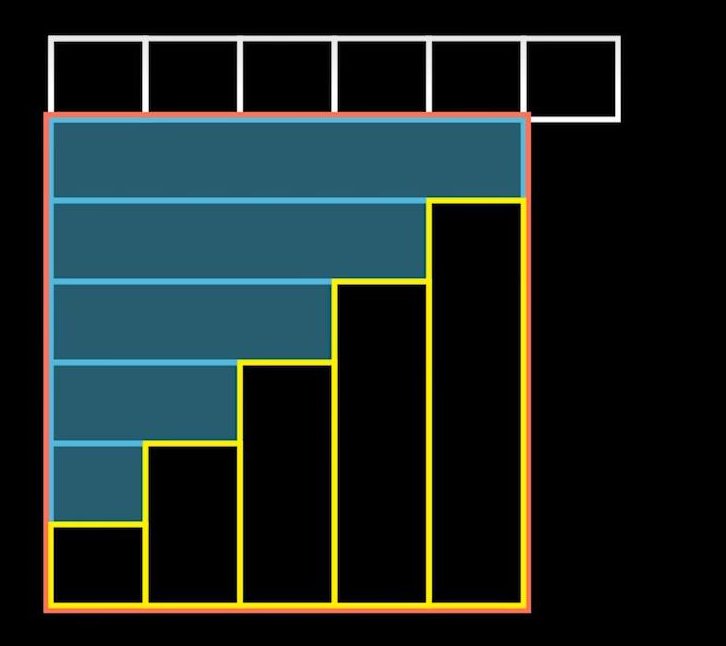
圖片來源：# 完全理解並深入應用樹狀陣列 | 支援多種動態維護區間操作

補全之後發現，這個總的面積，就是 \(S[x]\times x+S[x]\)，最後多出來的那個是最後一行，是我們補上的。

那我們看看黃色面積怎麼求：

\[\sum_{i=1}^{x}i\times t1[i] \]

這個東西好像比上面的好算一點（？

用字首和維護一下不就更好了！

我們記 \(t2[i]\) 來維護前 \(i\) 個 \(i\times t1[i]\) 的總和，那我們用樹狀陣列維護一下，不就也是 \(O(\log n)\) 了嗎。

我們最後用兩個樹狀陣列，來維護了兩個東西達到了區間修改區間查詢的目的。

對於我們的修改操作的程式碼，我們改成這樣：

inline void add(int x,int k){int xx=x;while(x<=n)t1[x]+=k,t2[x]+=(k*xx),x+=lb(x);}

我們很容易理解，就是多了個 t2[x]+=(k*xx)，因為我們說了是維護的前 \(i\times t1[i]\) 的總和，所以我們減去的時候要乘上 \(xx\)，並且要一直往上把所有包含他的節點都修改一遍。

再來看我們的查詢操作：

inline int ask(int x){int ans=0,xx=x;while(x>=1)ans+=(xx+1)*t1[x]-t2[x],x-=lb(x);return ans;}

裡面對於 \(t1\) 的累加應該很好理解，就是上面說的求整個矩形的面積，然後我們對於 \(t2\)，我們前說了就是維護前 \(i\times t1[i]\) 的總和，那麼我們這麼迴圈下去就是減去了 \(x\times t2[x]\)，然後這兩個一減，也就是上面的矩形總面積減去黃色面積，那不就是我們要求的藍色面積了嗎。

值得注意的是，\(t1\) 的思想是差分，\(t2\) 的思想是字首和，千萬不要搞混。

完整程式碼：

樹狀陣列區間修改區間求和 
#include<bits/stdc++.h>
#define int long long
#define N 1000100
using namespace std;
int n,m,a[N],t1[N],t2[N];
inline int lb(int x){return x&-x;}
inline void add(int x,int k){int xx=x;while(x<=n)t1[x]+=k,t2[x]+=(k*xx),x+=lb(x);}
inline int ask(int x){int ans=0,xx=x;while(x>=1)ans+=(xx+1)*t1[x]-t2[x],x-=lb(x);return ans;} 
signed main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=1;i<=n;i++)add(i,a[i]-a[i-1]);
	for(int i=1;i<=m;i++)
	{
		int op,l,r,x;
		cin>>op;
		if(op==1)
		{
			cin>>l>>r>>x;
			add(l,x);
			add(r+1,-x);
		}
		if(op==2)
		{
			cin>>l>>r;
			cout<<(ask(r)-ask(l-1))<<endl;
		}
	}
	return 0;
}

二維樹狀陣列

樹狀陣列比線段樹更容易擴充套件到二維，所以我們就來研究如何把它擴到二維。

我們在之前就已經說過，一維的樹狀陣列可以看作是一個點以自身為起點向左 lowbit 個單位的總和，那我們的二維的樹狀陣列的一點 \((x,y)\) 是不是也可以看作是向左 \(lowbit(x)\)，向上 \(lowbit(y)\) 個單位的矩形內元素的總和呢？

答案是 true。

單點修改區間查詢

例題：二維樹狀陣列單點修改區間查詢

我們對於這個操作，需要掌握的前置知識就是二維的字首和。

圖片來源：二維字首和詳解 - 沒有你哪有我 - 部落格園

我們可以看到利用二維字首和的思想，假設我們要求橫座標為 \(i\sim x\)，縱座標為 \(j\sim y\) 的矩陣內元素的總和，可以得到一個公式：

\[SUM=S[x][y]-S[x][j-1]-S[i-1][y]+S[i-1][j-1] \]

因為我們維護的相當於二維字首和，那麼我們就可以根據這個同樣去求解我們的二維樹狀陣列的區間查詢。

貼一下完整 code：

二維樹狀陣列單點修改區間查詢 
#include<bits/stdc++.h>
#define int long long
#define N 4100
using namespace std;
int n,m,t[N][N];
inline int lb(int x){return x&-x;}
inline void add(int x,int y,int k)
{
    while(x<=n)
    {
        int j=y;
        while(j<=m)
        {
            t[x][j]+=k;
            j+=lb(j);
        }
        x+=lb(x);
    }
}
inline int ask(int x,int y)
{
    int res=0;
    while(x>=1)
    {
        int j=y;
        while(j>=1)
        {
            res+=t[x][j];
            j-=lb(j);
        }
        x-=lb(x);
    }
    return res;
}
signed main()
{
    cin>>n>>m;
    int op,a,b,c,d;
    while(cin>>op)
    {
        if(op==1)
        {
            cin>>a>>b>>c;
            add(a,b,c);
        }
        if(op==2)
        {
            int ans=0;
            cin>>a>>b>>c>>d;
            ans=ask(c,d)+ask(a-1,b-1)-ask(c,b-1)-ask(a-1,d);
            cout<<ans<<endl;
        }
    }
    return 0;
}

我們在修改的時候，就像之前的一樣進行修改即可，只不過是多了一個 \(y\)，就是把原來的一層迴圈加了一層。

在區間求和的時候，我們就可以直接跟上面二維字首和一樣直接求出來了。

單次修改或查詢近似為 \(O(\log^{2}n)\)，總複雜度為 \(O(m\log^{2}n)\)。

單點查詢區間修改

二維樹狀陣列區間修改單點查詢

我們上面用了一維樹狀陣列的單點修改區間查詢的字首和思想，那麼我們是不是也可以用一維樹狀陣列的區間修改單點查詢的差分思想來轉到二維上來呢？

答案為 true。

我們還是看上面那張圖：

我們可以推出差分陣列中一個點的值為：

\[S[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1] \]

其實就是根據原陣列是差分陣列的字首和陣列來推的。

那我們就可以和之前的差分一樣，對於單點查詢我們就直接求字首和，也就是這樣寫：

inline int ask(int x,int y)
{
    int res=0;
    while(x>=1)
    {
        int j=y;
        while(j>=1)
        {
            res+=t[x][j];
            j-=lb(j);
        }
        x-=lb(x);
    }
    return res;
}

對的就是和上面的一摸一樣，呼叫的時候就直接 ask(x,y) 即可查詢當前下標為 \((x,y)\) 的點的值。

對於修改操作，我們從前面的字首和公式也能得到一些靈感，我們這樣寫：

add(a,b,k);
add(a,d+1,-k);
add(c+1,b,-k);
add(c+1,d+1,k);

同理 add 函數的程式碼和上面的是一樣的。

我們來看這四個操作，有沒有很像是字首和的四個矩形，只不過是換成了差分的 \(+1\) ？

我們還是根據上面差分陣列的公式來進行修改，我們就會發現實際上就是給 \((1,1),(c,d)\) 的矩形加了 \(k\)，我們由於是維護的差分陣列所以要 \(+1\)，然後由於我們兩個加起來肯定是中間有很多地方是不需要加的，比如 \((1,1),(a,d+1)\) 和 \((1,1),(c+1,b)\) 這兩個矩形，是多加了的，我們就給他減掉 \(k\)，然後你會發現 \((1,1),(a,b)\) 多減了一個 \(k\)，所以我們給他加回來，由於是差分，都是單點的修改。

每一次操作的複雜度勻以下約為 \(O(\log^{2}n)\)，總複雜度 \(O(m\log^{2}n)\)。

完整程式碼：

二維樹狀陣列區間修改單點查詢 
#include<bits/stdc++.h>
#define int long long
#define N 4100
using namespace std;
int n,m,t[N][N];
inline int lb(int x){return x&-x;}
inline void add(int x,int y,int k)
{
	while(x<=n)
	{
		int j=y;
		while(j<=m)
		{
			t[x][j]+=k;
			j+=lb(j);
		}
		x+=lb(x);
	}
}
inline int ask(int x,int y)
{
	int res=0;
	while(x>=1)
	{
		int j=y;
		while(j>=1)
		{
			res+=t[x][j];
			j-=lb(j);
		}
		x-=lb(x);
	}
	return res;
}
signed main()
{
	cin>>n>>m;
	int op,a,c,b,d,k;
	while(cin>>op)
	{
		if(op==1)
		{
			cin>>a>>b>>c>>d>>k;
			add(a,b,k);
			add(a,d+1,-k);
			add(c+1,b,-k);
			add(c+1,d+1,k);
		}
		if(op==2)
		{
			cin>>a>>b;
			cout<<ask(a,b)<<endl;
		}
	}
	return 0;
}

區間查詢區間修改

P4514上帝造題的七分鐘 - 洛谷

我們根據上面的字首和的定義，我們不難發現對於一個二維差分陣列，一個點 \((x,y)\) 的二位字首和就是：

\[SUM=\sum_{i=1}^{x}\sum_{j=1}^{y}\sum_{h=1}^{i}\sum_{k=1}^{j}S[h][k] \]

只是看這四重循壞就知道暴力肯定是不行的，那我們怎麼優化呢？

我們借鑑一下一維的區間查詢區間修改的做法，對於上面的式子，我們把後兩層列舉拆開看看。

我們可以發現 \(S[1][1]\) 出現了 \(x\times y\) 次，\(S[1][2]\) 出現了 \(x\times (y-1)\) 次，因為只有 \(j=1\) 的時候是沒有 \(S[1][2]\)的；同理我們可以推出一個一般的形式：\(S[h][k]\) 出現了 \((x-h+1)\times (y-k+1)\) 次，也就是說我們的式子可以化成下面的樣子：

\[SUM=\sum_{i=1}^{x}\sum_{j=1}^{y}S[i][j]\times (x-i+1)\times (y-j+1) \]

我們把後面的給展開一下：

\[SUM=\sum_{i=1}^{x}\sum_{j=1}^{y}S[i][j]\times (xy-xj-yi+ij-i-j+x+y+1) \]

最後我們稍微合併一下得到：

\[SUM=\sum_{i=1}^{x}\sum_{j=1}^{y}(xy+x+y+1)\times S[i][j]-j(x+1)\times S[i][j]-i(y+1)\times S[i][j]+ij\times S[i][j] \]

我們發現裡面只需要維護四個東西就可以完成我們的查詢操作了：\(S[i][j],S[i][j]\times i,S[i][j]\times j,S[i][j]\times i\times j\)

我們來看一下修改的程式碼：

inline void add(int x,int y,int k)
{
    for(int i=x;i<=n;i+=lb(i))
      for(int j=y;j<=m;j+=lb(j))
        t[i][j]+=k,ti[i][j]+=k*x,tj[i][j]+=k*y,tij[i][j]+=k*x*y;
}

我們在進行修改的時候就要對應我們每一個陣列維護的值來修改，修改的時候加上的值都要乘以對應的係數，而在主函數中，我們是跟差分的一樣來寫四次 add 操作。

而我們的求和操作需要這樣寫：

inline int ask(int x,int y)
{
    int res=0;
    for(int i=x;i>=1;i-=lb(i))
      for(int j=y;j>=1;j-=lb(j))
        res+=t[i][j]*(x*y+x+y+1)-ti[i][j]*(y+1)-tj[i][j]*(x+1)+tij[i][j];
    return res;
}

這裡乘起來的係數就是上面的公式推導的，對於我們已經維護好的我們就直接呼叫就好。

完整 code：

二維樹狀陣列區間修改區間求和 
#include<bits/stdc++.h>
//#define int long long
#define endl '\n'
#define N 2100
using namespace std;
int n,m,t[N][N],ti[N][N],tj[N][N],tij[N][N]; 
inline int lb(int x){return x&-x;}
inline int read(){int x=0,f=1;char ch=getchar();while(!isdigit(ch)){f=ch!='-';ch=getchar();}while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return f?x:-x;}
inline void print(int x){if(x>=10)print(x/10);putchar(x%10+48);}
inline void add(int x,int y,int k)
{
	for(int i=x;i<=n;i+=lb(i))
	  for(int j=y;j<=m;j+=lb(j))
	    t[i][j]+=k,ti[i][j]+=k*x,tj[i][j]+=k*y,tij[i][j]+=k*x*y;
}
inline int ask(int x,int y)
{
	int res=0;
	for(int i=x;i>=1;i-=lb(i))
	  for(int j=y;j>=1;j-=lb(j))
	    res+=t[i][j]*(x*y+x+y+1)-ti[i][j]*(y+1)-tj[i][j]*(x+1)+tij[i][j];
	return res;
}
signed main()
{
	char op;
	int a,b,c,d,k;
	cin>>op,n=read(),m=read();
	while(cin>>op)
	{
		if(op=='L')
		{
			a=read(),b=read(),c=read(),d=read(),k=read();
			add(a,b,k);
			add(a,d+1,-k);
			add(c+1,b,-k);
			add(c+1,d+1,k);
		}
		if(op=='k')
		{
			a=read(),b=read(),c=read(),d=read(); 
			int ans=ask(c,d)+ask(a-1,b-1);
			ans-=ask(a-1,d)+ask(c,b-1);
			cout<<ans<<endl;
		}
	}
	return 0;
}

寫在最後

以前稀裡糊塗的學了一遍樹狀陣列，現在來算是重修了一下。

突然發現發明這個東西的人好厲害，尤其是對於 lowbit 的使用，很奇妙。

有沒看明白的可以評論。