曲線藝術程式設計 coding curves 第二章 三角函數曲線(TRIG CURVES)
第二章 三角函數曲線(TRIG CURVES)
原作:Keith Peters
原文:https://www.bit-101.com/blog/2022/11/coding-curves/
譯者:池中物王二狗(sheldon)
blog: http://cnblogs.com/willian/
原始碼:github: https://github.com/willian12345/coding-curves
曲線藝術程式設計系列 第二章
這是與曲線相關最基礎簡單的一章,但我會用幾個不同的範例來演示。我不會深入詳細講解三角學,這裡不會演示什麼是90度角,鄰邊,對邊,斜邊和 soh-cah-toa(老外用來記憶三角函數的口訣)
我假定你已經瞭解了這些基本概念。如果你從未聽過,那麼你需要 google 一下,你會得到 18800000 個結果:
如果你對上面一段我說的東西一無所知,那麼先學上面我說的初中三角函數相關的知識。
等等,我在幹什麼?我失去了一個不要臉的推薦我自己部落格的機會(bit-101.com) ... 好吧, 這裡是有關我講解三角學的視訊列表(譯者注:請自己上外網搜尋 coding math _!),這是最佳學習資料,比剛才的 1.8 億搜尋結果要好的多,可能幫你省不少錢。
那從哪裡入開始入手呢...
好緊,你使用的程式語言中應該已經包含了許多三角學相關內建數學函數。也許是全域性的,也許在 Math 類內,在此篇中,你會和名為 sin、cos、tan 的這些東西打交道。這幾個函數代表了正弦、餘弦、正切,這些你在初中的時候肯定學過了(譯者:九年制義務教育的肯定學過,看看誰是漏網之魚…)
我們先從Sin 正弦開始。你傳入一個數值,它回給你一個數值。如果傳0.0,它返回 0.0。 隨著你傳入引數值的增長,返回的值也慢慢從 0.0到1.0,或接近1.0大概差不離。接著,隨著你傳入引數的繼續增長,返回值會從1.0 慢慢回落到0.0。 隨著你傳入的引數繼續增長,返回值會在 -1.0 至正 1.0 之間振盪。
試試:
for (i = 0.0; i < 6.28; i += 0.1) {
print(sin(i))
}
在你使用的編譯語言中,你可能需要使用 printIn 或 console 、log 之類的方法列印結果。但你應該可以獲取類似以下的列印結果:
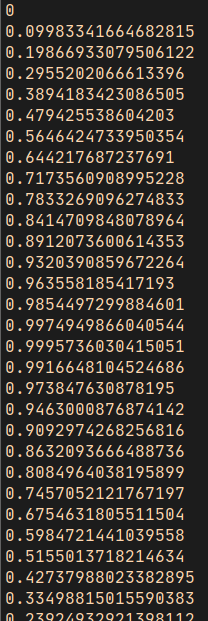
正如我預測的那樣,它從0 長到了 0.99957… 然後開始回落。輸出結果將繼續回落至- 0.9999923… 然後回到接近0.0
注意:它完成了一個圓迴圈,從 0-1 再從 -1 到 0,這不是巧合。因為 for 迴圈的結束點在設定在 6.28。 在大多數程式語言中這個值大約是 2*PI 或者說2 *3.14156… 三角函數基本使用弧度代替我們常用的角度。這是另一個我假定你已經知道的知識點。 比如一個弧度轉換成角度大概是57角度,3.14(PI)弧度是180 角度。6.28… (2 * PI)弧度是360角度。
所以,sin 結果從 0 到 1 到 -1 到 0,就是 0 - 360 度,或者說是 0 - 6.28 弧度
如果你改變了 for 迴圈的結束點在 PI (大多數程式語言會有PI這個常數)結果值將會從 0.0 至 1.0 再至 0.0 ,這就是半個圓周期。
把它們應用到曲線上
好的,讓我們畫個正弦波吧。設定你的繪製區域 800x500。 將這兩個值設定成變數(或常數) width 寬度,height 高度。 然後用一個迴圈將變數 x 從 0 加到 800。用 width 這個變數。 我們使用 x 計算出正弦值用於 y 。 我們再在 y 值上加上 height 值的一半,這樣正弦波就會顯示在圖象中央位置了。畫一條線段從 x 至 y,搞定。
記住,這全是虛擬碼,你需要轉換成你正真在使用的程式語言(在第一章解釋過了)。
width = 800
height = 500
canvas(width, height)
for (x = 0; x < width; x++) {
y = height / 2 + sin(x)
lineTo(x, y)
}
stroke()
依據你所使用程式語言對應的繪圖 api ,在使用 lineTo api 前 你可能先需要使用 moveTo(0, height/2) 。當你搞定後應該會得到如下結果

這就是正弦波了,也許不如你預期的那樣。有裡有兩個問題,但很好這兩個問題引出了我們要討論的兩個東西: 波長/頻率 和 振幅。上圖中太多波了--波長太短(或者說頻率太高),波有點像點了- 振幅太低了。
振幅
振幅很容易拿捏。正弦值從 -1.0 至 1.0 ,我們僅需要將這些值乘以對應的振幅值就可以了。 canvas 高度乘以類似 0.45 這樣的值可以讓波形高度小於 canvas 的高度
width = 800
height = 500
amplitude = height * 0.45
canvas(width, height)
for (x = 0; x < width; x++) {
y = height / 2 + sin(x) * amplitude
lineTo(x, y)
}
stroke()
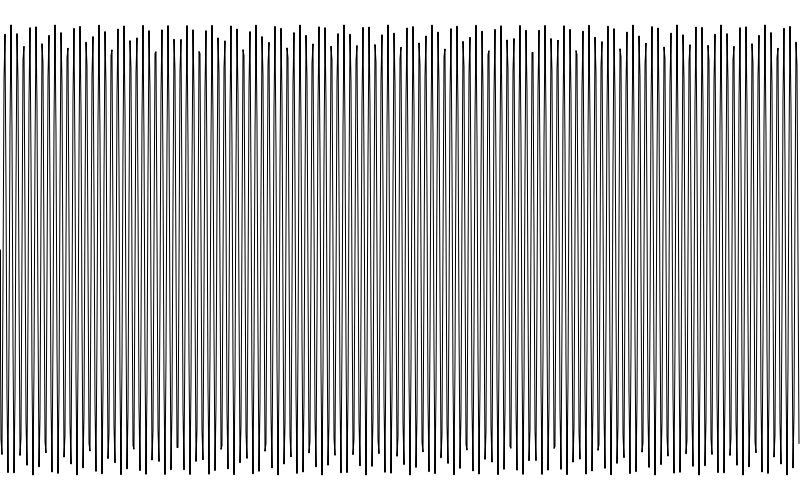
現在高度我們是有了,但波還是太多了以致於我們不能說這就是正弦波。我們將在下面章節解決這個問題。
波長與頻率
波長…. 等等, 波的長度,或者說兩個連續週期相同點之間波的長度。在真實世界中,它們是真實測量的物理距離單位從米到納米,取決於你測量的是何種波
另一種橫量波形的是頻率 ——— 一個時間間隔(或一段距離空間)內波形數量
波長與頻率反向相關(反比)。短波(兩個波形很近)等於高頻(給定的一段距離內擁有很多波形)。長波等於低頻。
你可以用它的兩個特性編寫程式碼,讓我們從頻率開始。
頻率
我們一般用「週期數/每秒」(cps)來代指一段距離內的週期數。以收音機收到音訊波舉例,我們可以通過每一秒接收到了多少來統計。 專業名詞「赫茲」簡寫為「Hz」代表每秒擁有多少個週期。100Hz 代表每秒100個週期。1千赫茲代表1000 cps, 1兆赫代表100萬cps …
因為我們不是處理動態的波,在給定的空間內測量一個週期內波的頻率會更容易。 想要產生什麼樣的結果取決於你給定的應用程式,既然我們是在 800 畫素寬度內繪製正弦波,我們說的頻率為 1 ,意為著一個正弦波圖形應該穿越整個畫布。
這裡用了一點點數學,我把程式碼扔這了,然後我們繼續分析過一遍
width = 800
height = 500
amplitude = height * 0.45
freq = 1.0
canvas(width, height)
for (x = 0; x < width; x++) {
y = height / 2 + sin(x / width * PI * 2 * freq) * amplitude
lineTo(x, y)
}
stroke()
首先我們建立了一個 freq 變數並設值為1.0
我們替換之前給 sin 的 x 值,將 x 乘以 canvas 寬度。 x / width 迴圈結果過程值會變為從 0.0 到 1.0。
然後我們再乘以 PI * 2 這會讓值 0.0 至 6.28… , 這個非常像最初的例子中得到的結果。這個例子會讓結果從 0 到 1再到 -1 然後回到 0,剛好就是你看到的一個週期。
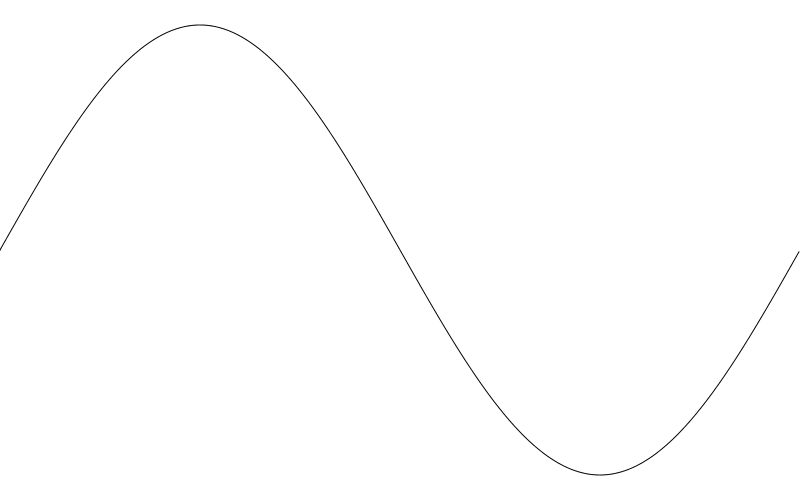
最後,我們乘以 freq 頻率。 當前設定的是 1.0 , 我們得到的仍然是一個週期。所有的這些設定你將會看到下圖:
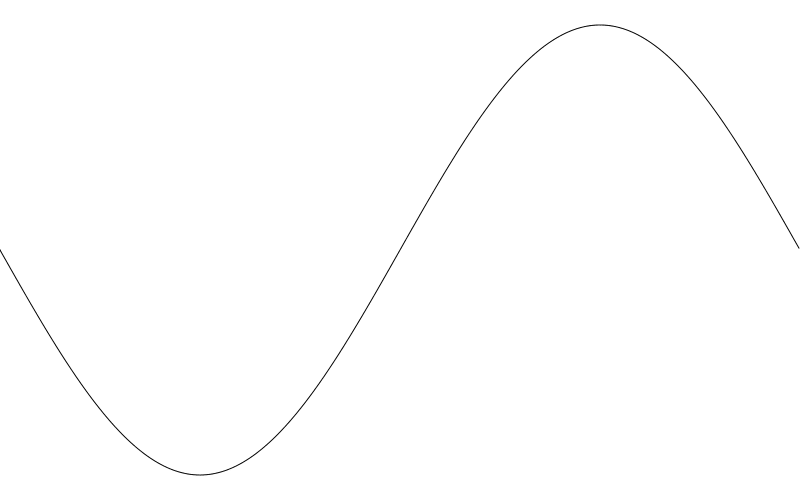
好的,像那麼回事兒了。但是一般我們常用的正弦圖波形是先向上再向下的。如果你看到的是先向下再向上,就如我們這裡的例子中展示的那樣,那是因為我們使用的 y 軸是向下的與迪卡爾座標系的 y 軸相反。 如果你瞭解如何使用繪圖 api 2d transform 方法, 你自己就能搞定。我將用簡單方式修復它,在呼叫 lineTo 時將 y 變成 height - y 就妥了。
width = 800
height = 500
amplitude = height * 0.45
freq = 1.0
canvas(width, height)
for (x = 0; x < width; x++) {
y = height / 2 + sin(x / width * PI * 2 * freq) * amplitude
lineTo(x, height - y)
}
stroke()
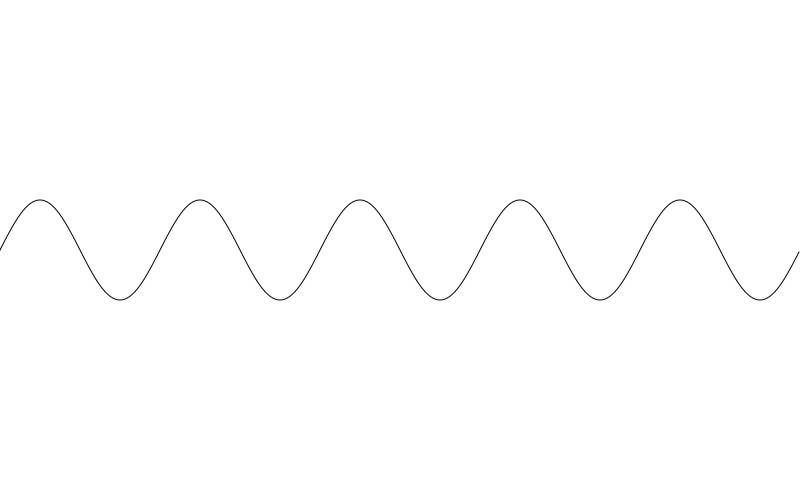
現在,你可以嘗試改變 amplitude 和 freq 這兩個變數建立不同的波形圖。下面是我將 amplitude 設為 50 freq 設為 5 的結果
波長
現在,讓我們用波長代替頻率來重新實現一下。在這例子中,我們將用波長表示一個完整波形週期內佔用的畫素。 現在我們可以這樣說:我想要一個 100 畫素長的週期波形。
width = 800
height = 500
amplitude = height * 0.45
wavelength = 100
canvas(width, height)
for (x = 0; x < width; x++) {
y = height / 2 + sin(x / wavelength * PI * 2) * amplitude
lineTo(x, height - y)
}
stroke()
此番在sin函數呼叫時,我們將x 除以 wavelength。這樣前 100 畫素內,我們將得到值 0.0 至 1.0, 緊接著下一個 100 畫素 1.0 至 2.0等 。
然後值再乘以 2PI,所以 100 畫素內每一個畫素都會乘以 6.28 中的某一個值…並執行一個完整的波形週期
結果如下圖
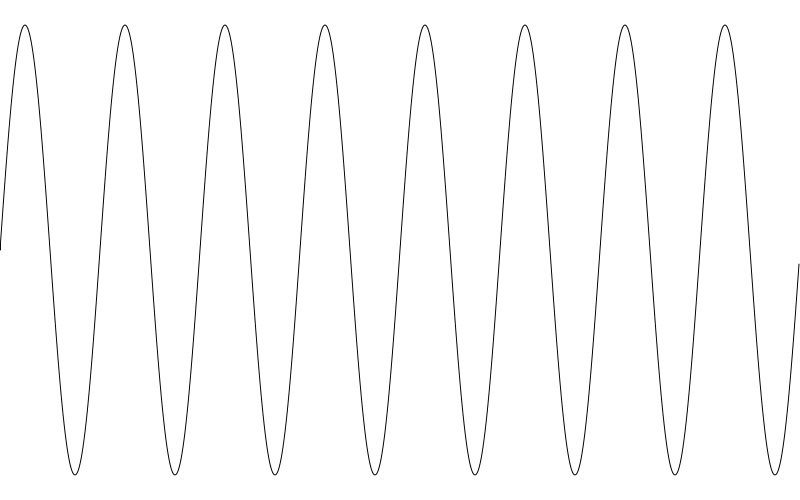
由於我們的 canvas 畫布寬 800 畫素 波長設定為 100 畫素,我們如期得到了 8個完整週期波型。
Resolution
A quick word about resolution. Here, we are moving through the canvas in intervals of a single pixel per iteration, so our sine waves look pretty smooth. But it might be too much. If you are doing a lot of this and you want to limit the lines drawn, you can do so, with the possible loss of some resolution. We’ll just create a res variable and add that to x in the for loop and see what that does. We’ll start with a resolution of 10.
解析度
簡單解釋一下解析度(譯者注:不是物理上的解析度,只是繪製過程中迴圈內的步幅)。這裡,for迴圈每一次迭代在canvas畫布中走過1畫素距離, 這樣讓我們的正弦波看起來挺潤的。但繪製次數也太多了。如果在你的繪製中想減少一些線條繪製,你可以通過縮小減少解析度來實現。我們建立一個叫 res 的變數 並將它新增進 x 在 for 迴圈內看看會發生什麼 。 我們先從 10 開始
width = 800
height = 500
amplitude = height * 0.45
freq = 3
res = 10
canvas(width, height)
for (x = 0; x < width; x += res) {
y = height / 2 + sin(x / width * PI * 2 * freq) * amplitude
lineTo(x, height - y)
}
stroke()
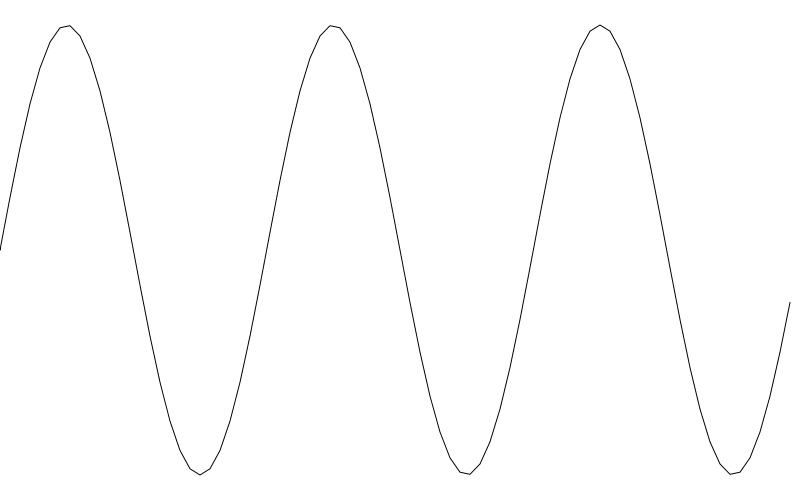
On the plus side, we are drawing only 10% of the lines we were drawing before. But you can already see that things have gotten a bit chunky. Going up to 20 for res reduces the lines drawn by half again. But now things are looking rough.
從好的的一方面來說,我們只繪製了之前繪製線條的 10%。但你已經可以看到了線條有一點點塊狀化了。如果將 res 加到 20 繼續減少線條繪製,這回線條看起來就很粗糙了
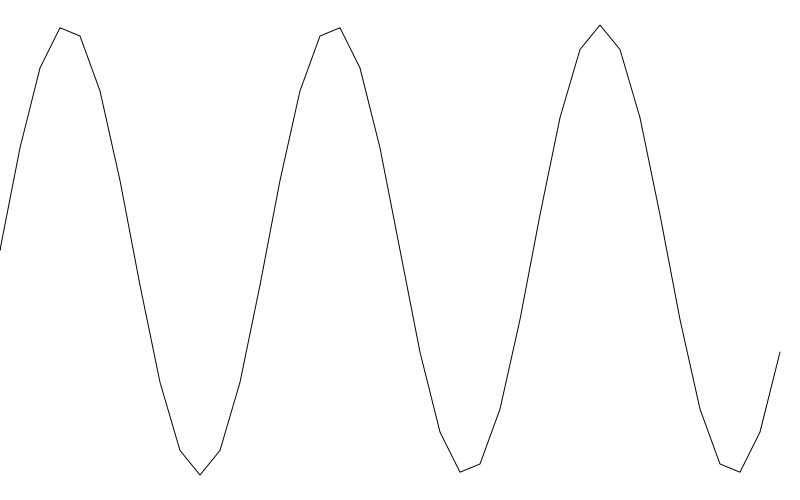
重點是你知道這個有這個選項的,在使用過程中在效能與效果上權衡利弊
Cosine
I’m going to keep this one really quick. Because everything I’ve said about sine holds true for cosine, except that the whole cycle is shifted over a bit. Going back to a single cycle and simply swapping out cos for sin …
餘弦
在餘弦上面我會講快一佔,因為基本知識已經在上面正弦中普及過了同樣適用於餘弦, 除了餘弦影象相對正弦是翻轉過來的。回到單迴圈波形簡單的將 sin 替換成 cos 就行。
width = 800
height = 500
amplitude = height * 0.45
freq = 1.0
canvas(width, height)
for (x = 0; x < width; x++) {
y = height / 2 + cos(x / width * PI * 2 * freq) * amplitude
lineTo(x, height - y)
}
stroke()
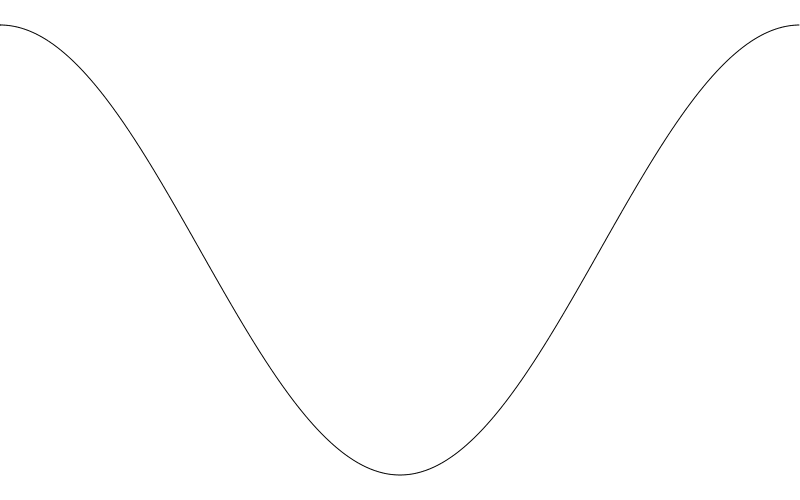
這裡,我們輸入 0.0 得到的是 1.0 然後往下掉到 0.0, -1.0 再回到 0.0 最後再回 1.0 結束。 就像是我們將0.0 慢慢變到 2 * PI . 就像是同樣的波形轉了 90 度(或都說 PI / 2 弧度)。如果我們將頻率調高一點,更容易看清
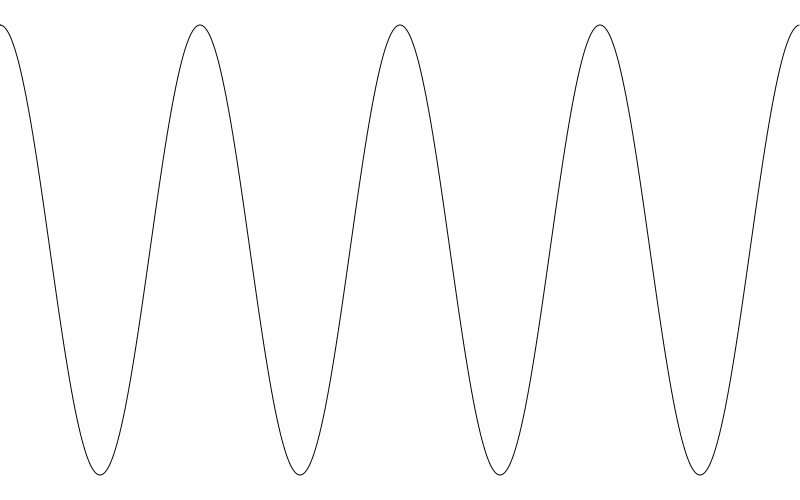
I don’t really have a whole lot to say about cosine waves for this post. But we’ll be revisiting them again later in the series.
在此章中我不會說太多餘弦,但後面系列中我們還會再涉及到餘弦相關知識。
可複用的函數
至此學到的相關知識我們可以封裝一個可重用的函數,它接收兩個位置引數在兩點之間繪製一個正弦波。再次,我先放虛擬碼在下面,然後慢慢解釋。
function sinewave(x0, y0, x1, y1, freq, amp) {
dx = x1 - x0
dy = y1 - y0
dist = sqrt(dx*dx + dy*dy)
angle = atan2(dy, dx)
push()
translate(x0, y0)
rotate(angle)
for (x = 0.0; x < dist; x++) {
y = sin(x / dist * freq * PI * 2) * amp
lineTo(x, -y)
}
stroke()
pop()
}
此函數接收 6 個引數,x 和 y 座標點表示開始與結束點,還有頻率和振幅。
我們通過 dx 和 dy 獲取計算兩點間穩中各軸間的距離。
然後根據 dx 和 dy ,我們用勾股定理計算出兩點之間的距離。sqrt 函數應該在所用的程式語言中是內建的。
然後我們通過 atan2 內建函數計算出角度,如果至此你不知道發生了啥,那麼我建議你找一找我以前發表過的文章(譯者注:作者部落格中的文章 有過介紹,並且出版過 flash 基礎動畫,flash 高階動畫等書籍)。
現在,這個函數內假定你的繪製api 有2d transform 變形能力。如果是的話,transform 功能大概率會有 push 和 pop,入棧與出棧功能 。以HTML Canvas api 舉例, 它的功能 api 會像是這樣 context.save() 和 context.restore();
我們將當前transform push 到棧中我們就可以對canvas整個執行變形繪製,然後在繪製完畢後再 restore 恢復到進入棧前的狀態
(譯者注:push 和 pop ,save 和 restore 等類似的功能的存在是由於2d 圖形繪製涉及到變幻功能時使用的是線性代數中矩陣轉換功能實現,相關知識請自行學習大學數學,反正我在上學的時候是沒學好。後來是看 3blue1brown 出的線性代數視訊理解的… 好吧我是學渣承認我是假裝理解……這不重要,繼續)。
然後我們將上下文移動到開始點並旋轉到計算出來的角度.。 在這個點我們僅需要用 dist、freq、amp 這幾個變數 繪製一個正弦波,正如我們之前所做的那樣。
當我們的 canvas 上下文移動到了我們希望的起始點時,我們直接呼叫用 lineTo(x, -y) 實現正確的正弦波繪製就像之前那樣。
當搞定以上步驟後,呼叫 stroke 來顯示出路徑,還要呼叫 pop(或 restore 或其它什麼類似的 api )恢復到函數繪製前的狀態。
現在我們就可以像這樣呼叫函數了
width = 800
height = 500
canvas(width, height)
sinewave(100, 100, 700, 400, 10, 40)
這次繪製了一條正弦波形在起始 100,100 位置 至 700, 500 結束頻率 10, 振幅 40.
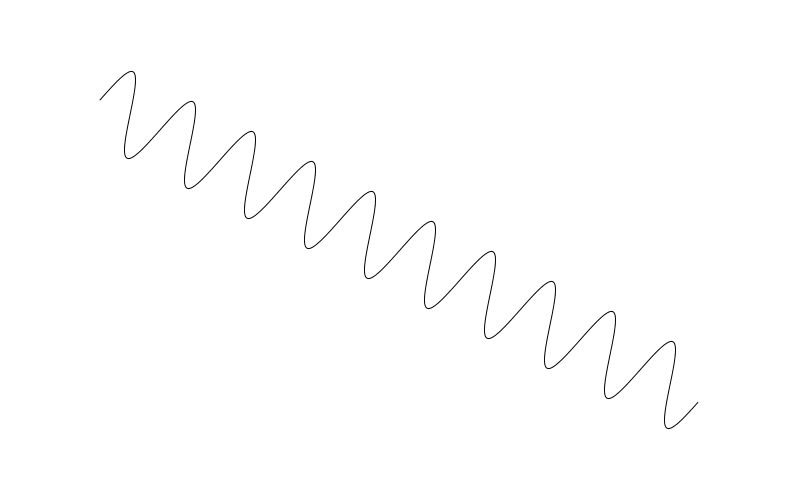
If your drawing api does not have transform methods, I pity you. You can still do this kind of thing, but it will be much more complex. And beyond the scope of this post.
如果你正使用的程式語言沒有 transform 這一類函數,那你可太慘了。雖然你依然可以實現類似的效果,但會非常複雜,這超出了本篇的範圍。
在博文下方評論內有人提到 frequency 這一詞可能會導致困惑,這詞隱含的意思會是 A 點 B 點之間一共包含多少個週期迴圈,所以一個長波的繪製意謂著比同頻繪製一個較短的 wavelength 要大。為解決這一點,你可能希望用wavelength 代替frequency. 這將確保所有具有相同波長的波看起來都很相似,無論它們有多長。另一個選項是將frequency與 frame 影格率聯絡起來,如:「每1000畫素有多少個週期」,諸如此類的。無論怎麼做都需要根據你自己的需求來,所以選擇權交給你。
(譯者注: 這是作者博文評論區有有人提出作者使用 frequency 頻率這個變數控制波形有歧義,因為按現在的 sinewave 函數在繪製兩點距離不同時,所產生的圖形,波長是不一樣的。所以有人提議用 wavelength 代替 frequency 來實現,這樣不管兩點距離是多少,波長總是一樣的,感覺作者的意思就是情況有很多,你可以根據自己的需求調整,調整很簡單我試了一下, 迴圈中改成這句就行 y = sin(x / wavelength * PI * 2) * amp; 傳 freq 變成 傳 wavelegnth。原始碼中我用 wave-function-wavelength.html 演示了一下)
.
正切
繪製正切曲線比起正弦與餘弦來講沒啥大用,但為了完整性還是講一講。
不像之前兩個函數,正切自身的值沒有限制在 -1 至 1 的範圍,事實上,它範圍是無限的,讓我們像之前對正弦那樣輸出檢視一下正切值是啥樣。
for (i = 0.0; i < 6.28; i += 0.1) {
print(tan(i))
}
你基本上可以看到類似下面的輸入結果:
再一次,我們從 0 開始,但它迅速增長至 14,接著直接跳到 -34,就很迷。這些值被截斷了因為我們用的是相對較大的 0.1 作為步長。 實際是這樣的,隨著輸入值接近 PI/2 弧度(或90度角)數值快速增長到正無窮大,一旦超過了這個值,它又向下跳到負無窮,很快在 PI (180 度角)又升到 0.0 ,然後在到達 2 * PI (360 度)前重複這一回圈。這不是一個線性過程雖然它在接近和離開 0 時繪製了一條曲線,讓我們用頻率實現一個正切波形看看
width = 800
height = 500
amplitude = 10
freq = 1.0
canvas(width, height)
for (x = 0; x < width; x++) {
y = height / 2 + tan(x / width * PI * 2 * freq) * amplitude
lineTo(x, height - y)
}
stroke()
Same thing here again, but swapped out tan for sin. I also reduced the amplitude just so we could see the curve better. In fact, it’s probably a misnomer to talk about the amplitude of a tangent wave since its amplitude is actually infinite. But this value does affect the shape of the curve.
和之前程式碼一樣,只是將 sin 替換成了 tan。我還減少了 amplitude 值以更好的觀察曲線。事實上,振幅用在這裡解釋可能用詞不當,因為這裡的振幅是無限的。但這個值的確會影響曲線形狀。
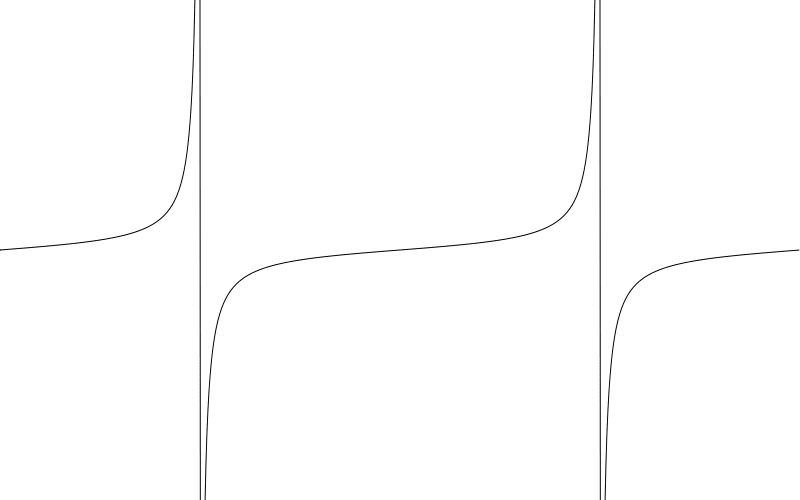
有一點需要注意,這些接近垂直的線是從正無窮到負無窮。這些不是正切影象上的部分。數學上來講,這暗示著正切值在這條垂直線上有某個點會有某個值,但確不是。事實上在 90-270 度之間這個值是 undefined 。這些值前後接近正負無窮。不確定這特性對你有沒有用,就這樣吧。
總結
我們已經學習了這個系列中最初部分的曲線。這是好的基礎,後面我們將會在其它曲線中用到這裡學習到的知識和相應的函數。 回頭見。
本章 Javascript 原始碼 https://github.com/willian12345/coding-curves/tree/main/examples/ch02
部落格園: http://cnblogs.com/willian/
github: https://github.com/willian12345/