淺談掃描線
掃描線
掃描線一般運用在圖形上面,它和它的字面意思非常相似,就是拿一根線,在圖形上面掃來掃去。我們一般用它來解決圖形的面積,周長,二位數點等問題。
Atlantis 問題
在二維座標系上,給出多個矩形的左下以及右上座標,求出所有矩形構成的圖形的面積。
我們當然知道,如果資料範圍很小,我們可以直接暴力,也就是先都加起來,然後再列舉一下把重複的減去;但如果資料範圍過大,我們暴力肯定是不行的,這個時候就可以用到我們的掃描線了。
假設我們現在有一根線,從下往上開始掃描:
(這是張動圖可能導成pdf就掛了)
我們發現,我們把整個圖形分成了如圖各個顏色不同的小矩形,那麼這個小矩陣的高就是我們掃過的距離,那麼剩下了一個變數,那就是長在不斷地變化。
我們一般用線段樹來維護矩形的長,我們給每一個矩形的上下邊進行標記,下面的邊標記為 \(1\),上面的邊標記為 \(-1\),每遇到一個矩形的時候,我們就知道了標記為 \(1\) 的邊,我們就加進來這一條矩形的長,等到掃描到 \(-1\) 的時候,證明這一條邊需要刪除,就刪去,利用 \(1\) 和 \(-1\) 可以輕鬆的到達這種狀態。
我們一般還需要用到離散化。
面積並
我們結合例題來看一下:
我們前面說要用線段樹來做,我們用它來維護當前的矩形的長。
我們考慮到我們的線段樹維護的東西都是點,但是我們需要維護的是區間,那麼我們可以把區間下放到點上,也就是每一個葉子節點維護的是一個線段,而我們用 \(l\),也就是當前點的左端點,以及 $r+1 $ 來達到詢問當前節點區間的左右端點的目的。
我們先來看主函數:
signed main()
{
n=read();
for(int i=1;i<=n;i++)
{
x11=read(),y11=read(),x22=read(),y22=read();
X[2*i-1]=x11,X[2*i]=x22;
e[2*i-1]=(sb){x11,x22,y11,1};
e[2*i]=(sb){x11,x22,y22,-1};
}
n*=2;
sort(e+1,e+n+1,cmp);
sort(X+1,X+n+1);
int tot=unique(X+1,X+n+1)-X-1;
// cout<<"tot:"<<tot<<endl;
build(1,1,tot-1);
int ans=0;
for(int i=1;i<n;i++)
{
change(1,e[i].l,e[i].r,e[i].flag);
ans+=e1[1].len*(e[i+1].h-e[i].h);
}
cout<<ans<<endl;
// for(int i=1;i<=n;i++)cout<<X[i]<<" ";cout<<endl;
return 0;
}
\(X\) 陣列是用來存放所有點的橫座標,因為我們是要維護區間的話,不可能每一個點都維護到,所以只存放有給定點的座標,\(e\) 是定義的結構體用於存放每一個矩形的資訊,我們需要把他給存放下當前矩形的資訊,其中 \(X[2i-1]\) 是當前矩形的左端點橫座標,\(X[2i]\) 是當前矩形的右端點橫座標,\(e[2i-1]\) 是當前矩形的下表面,\(e[2i]\) 是當前矩形的上表面,因為我們說了如果要是碰到了下表面,我們就需要給他加進去,一旦碰到上表面,說明這個矩形完成了,可以出去了。兩個 sort 第一個是給矩形的上下表面按高度排序,保證是從下往上遍歷的,不會出現負數,後面的是進行排序後用 unique 進行離散化,然後就開始建樹。因為我們是把線段放到左端點上,所以是 \(tot-1\) 個。再往後,我們進行 change 操作來對當前掃到的矩形長的長度做修改,然後用上一個的高度減去當前點的高度,計算當前掃到的面積。
再來看 change 操作:
inline void p_p(int x)
{
int l=e1[x].l,r=e1[x].r;
if(e1[x].sum)e1[x].len=X[r+1]-X[l];
else e1[x].len=e1[ls].len+e1[rs].len;
}
inline void change(int x,int nl,int nr,int c)
{
int l=e1[x].l,r=e1[x].r;
if(X[r+1]<=nl||nr<=X[l])return ;
if(nl<=X[l]&&X[r+1]<=nr)
{
e1[x].sum+=c;
p_p(x);
return ;
}
change(ls,nl,nr,c);
change(rs,nl,nr,c);
p_p(x);
return ;
}
我們的 change 裡面是用來修改當前掃到的矩形的長的長度總和的。
如果要是當前的區間右端點在要改的左端點的左邊,那肯定不會包含,直接退出;如果當前區間左端點在要改的右端點的右邊,那肯定也不包含,直接退出。
後面如果遇到包含的區間就直接改 \(sum\),然後更新。
這個更新函數也就是 p_p 是對於所有的掃到的線段長度進行求和返回到上面,如果沒有掃到就直接更新兒子節點,為什麼呢?因為一開始的兒子節點長度都是 \(0\),葉子節點沒有兒子節點,預設也是 \(0\)。
至此我們完成了這個奇妙的演演算法!
周長並
既然求了面積,那就再來看看求周長吧。
P1856[IOI1998] [USACO5.5] 矩形周長Picture - 洛谷
看到題目給的圖片:什麼亂七八糟的
我們來試著找找有沒有什麼規律:
我們先來看豎著的線。
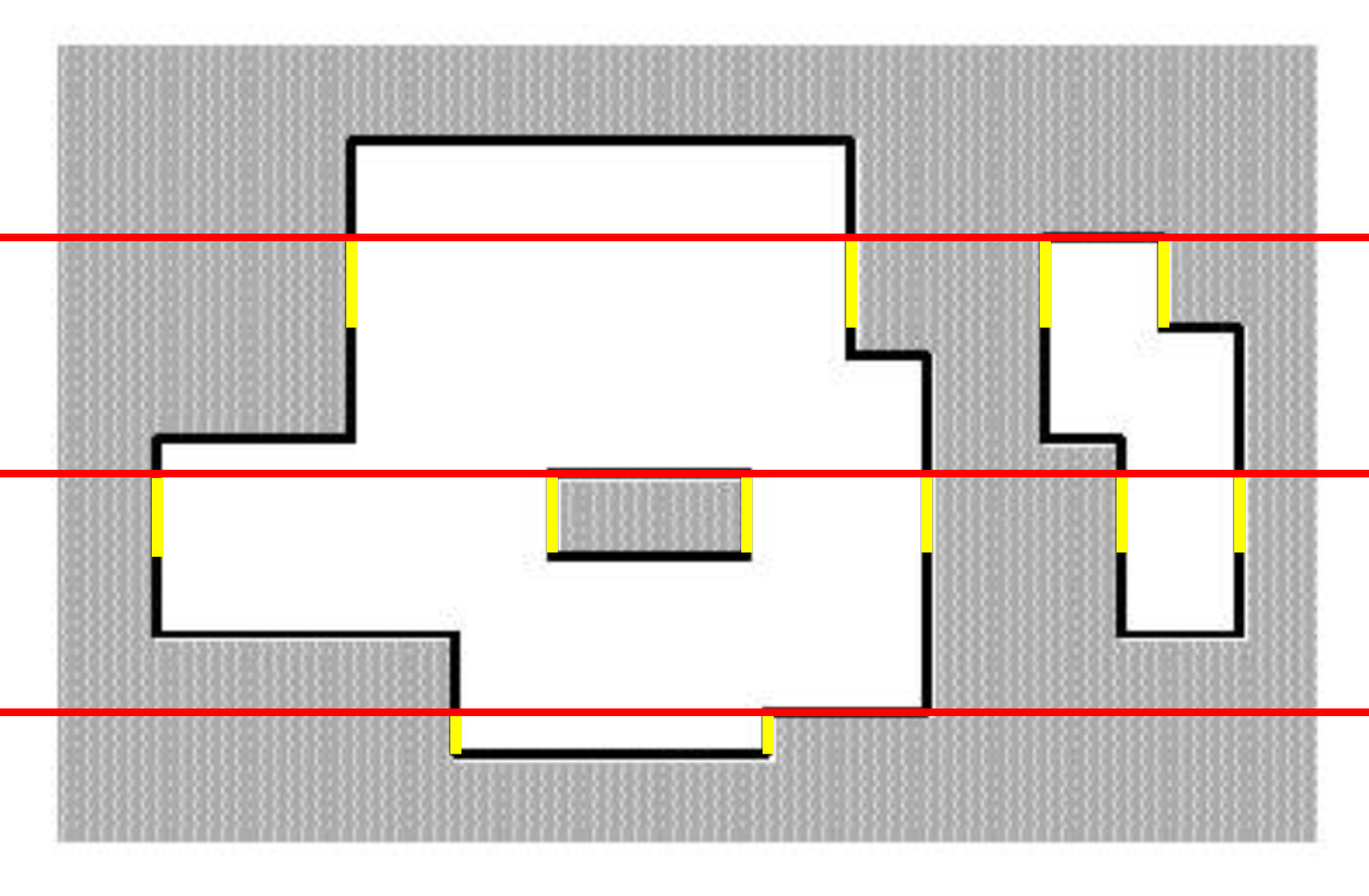
我們很容易發現,我們當前截到的線段數量,乘上 \(2\),然後再乘以當前點掃過的高度,不就是我們當前掃到的所有矩形的豎邊的長度總和嗎?
然後我們再來看橫邊。
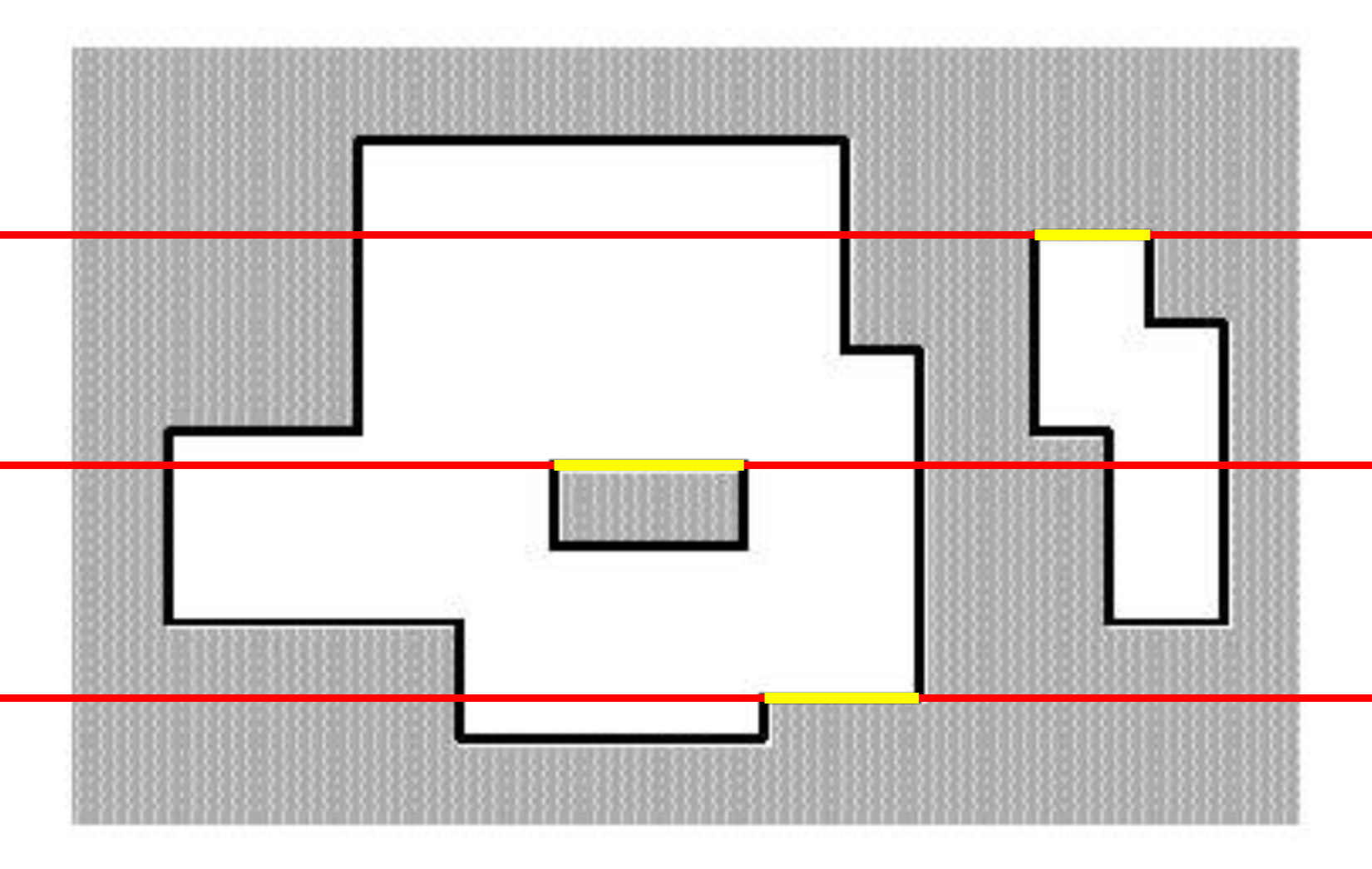
我們手模一下不難發現,我們在往上不斷平移線段的時候,我們發現,當前的長,也就是和線段重合的長度,是上一次的長度與這次長度做差的絕對值!
為什麼是絕對值?如果是一開始的時候,長會越來越大,就是這一次減去上一次的值,而到了後面,就是上一次長度減去這一次長度的值了。
所以我們需要加個絕對值。
知道怎麼算周長了,那我們直接套線段樹吧!
但是我們上面說過,計算豎邊的時候,我們需要知道當前掃描線上線段的數量。
所以我們的線段樹要多維護幾個東西:當前線段左右端點是否被覆蓋,以及當前區間內掃描線上的線段數量。
具體結合程式碼來分析:
signed main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>x11>>y11>>x22>>y22;
X[2*i-1]=x11,X[2*i]=x22;
e[2*i-1]={x11,x22,y11,1};
e[2*i]={x11,x22,y22,-1};
}
n*=2;
sort(e+1,e+n+1,cmp);
sort(X+1,X+n+1);
int tot=unique(X+1,X+n+1)-X-1;
build(1,1,tot-1);
int res=0;
for(int i=1;i<n;i++)
{
change(1,e[i].l,e[i].r,e[i].flag);
res+=abs(pre-t[1].len);
pre=t[1].len;
res+=2*t[1].c*(e[i+1].h-e[i].h);
}
res+=e[n].r-e[n].l;
cout<<res<<endl;
return 0;
}
和上面一樣的部分就不說了,看不一樣的。
對 \(e\) 進行排序的時候,我們先按高度排序,然後高度相同就把下底面放前面,因為不這樣做就會把這條邊多掃一遍,雖然在面積中無影響但是對於周長影響挺大的。
其中 \(pre\) 表示上一次掃描線上的線段總長度。
最後為什麼有一個第 \(n\) 個矩形的單獨計算呢?因為我們上面是列舉到 \(n-1\),最後一條邊是取不到的,所以我們最後算上。
inline void p_p(int x)
{
int l=t[x].l,r=t[x].r;
if(t[x].sum)
{
t[x].len=X[r+1]-X[l];
t[x].lc=t[x].rc=1;
t[x].c=1;
}
else
{
t[x].len=t[ls].len+t[rs].len;
t[x].lc=t[ls].lc,t[x].rc=t[rs].rc;
t[x].c=t[ls].c+t[rs].c;
if(t[rs].lc&&t[ls].rc)t[x].c--;
}
}
inline void change(int x,int nl,int nr,int c)
{
int l=t[x].l,r=t[x].r;
if(X[l]>=nr||nl>=X[r+1])return ;
if(nl<=X[l]&&nr>=X[r+1])
{
t[x].sum+=c;
p_p(x);
return ;
}
change(ls,nl,nr,c);
change(rs,nl,nr,c);
p_p(x);
return ;
}
更新函數裡面,\(lc,rc\) 分別表示當前節點代表的線段的左右端點是否被覆蓋,\(c\) 是此區間內的線段數量,如果 \(sum\) 有值,我們就直接更新,標記當前線段左右端點都被覆蓋,然後就是當前區間是一個線段,\(c\) 標記為 \(1\)。
如果此區間內不是都被覆蓋,那就先累加長度,隨後判斷此區間的端點覆蓋情況,如果左區間左端點被覆蓋,那麼此區間的左端點也被覆蓋,反之對於右區間的右端點也成立,先粗略把左右區間的線段數累加起來,後面判斷交點是否都被覆蓋,如果都被覆蓋,說明中間是一整段的,直接把線段樹減一即可。
對於 change 函數,和之前的面積修改一樣。
然後我們就把周長的問題也給解決了!
但是掃描線的作用不僅限於此。
二維數點
給一個長為 \(n\) 的序列,有 \(m\) 次查詢,每次查區間 \([l,r]\) 中值在 \([x,y]\) 內的元素個數。
這個問題就叫做二維數點。我們可以發現等價於我們要查詢一個二維平面上矩形內的點的數量和。
最簡單的方法就是掃描線 + 樹狀陣列。
很顯然,這個問題是一個靜態的二維問題,我們通過掃描線可以將靜態的二維問題轉換為動態的一維問題。維護動態的一維問題就可以使用資料結構,這裡可以使用樹狀陣列。
先將所有的詢問離散化,用樹狀陣列來維護權值,對於每次詢問的 \(l\) 和 \(r\),我們在列舉到 \(l-1\) 的時候統計當前位於區間 \([x,y]\) 內的數的數量 \(a\),繼續向後列舉,列舉到 \(r\) 時統計當前位於區間 \([x,y]\) 內的數的數量 \(b\),\(b-a\) 即為該次詢問的答案。
參考:oiwiki以及https://ncc79601.blog.luogu.org/scan-line