今天給大家分享一個新的統計方法，叫做響應面分析，響應面分析是用來探究變數一致性假設的（Congruence hypotheses）。本身是一個工程學方法，目前在組織行為學，管理，市場行銷等等領域中使用越來越多。

Congruence hypotheses state that the agreement (i.e., congruence) between two constructs should positively (or negatively) affect some outcome variable. Such hypotheses play a central role in many disciplines, for example, Marketing (Kim & Hsieh, 2003), Organizational Behavior (Caniëls & Veld, 2019), and Purchasing (Caniëls, Vos, Schiele, & Pulles, 2018).

響應面分析尤其是在探究一致性和不一致性作用的時候是最佳選擇，就是說比如你有兩個自變數，一個因變數，你想看看如果這兩個自變數都同時一致性變化（同時增大或減小）和同時不一致變化（一個增大另一個減小）的情況下，因變數如何變化。這個時候一定記得使用響應面分析。

response surface analysis (RSA) is an approach that allows examining the extent to which combinations of two predictive variables relate to one outcome variable. The method is particularly interesting in cases where (in)congruence between the two predictive variables is a central consideration of the study.

一致性假設的檢驗需要涉及到多項式迴歸，而響應面分析的優勢在於可以其可以將多項式迴歸的結果用3D畫出來，從而使得我們看清楚各種自變數組合情形下因變數的變化情況。並且通過多項式的係數情況對相應假設進行證明。

The foundation of RSA is the visualization of the results of the regression equation on a three-dimensional graph . Instead of directly interpreting the results of the polynomial regression analysis, the coefficients are used to examine what is called a ‘response surface pattern’ . The response surface is a graph that provides a three-dimensional visual representation of the data to aid interpretation

並且響應面分析還可以檢驗互動，且不受線性假設限制，今天結合兩篇比較有意思的文獻給大家分享響應面分析的理解和具體做法。

理論理解

想想如果你不知道響應面分析，你想研究兩個變數的不一致對結局的影響你會怎麼做？比如你想研究父母期望x1和兒童興趣x2對兒童成就y的影響，想要驗證是不是父母期望和兒童興趣的一致性越強，將來兒童的成就越高？你怎麼做?

計算一個新變數？x1-x2再取個絕對值，作為新的自變數，叫做兩者差距？用這個新變數去做y的迴歸分析？

估計大部分同學首先想到的就是這麼樣操作。

這裡面有兩個問題：1是資訊丟失了；2是你不能知道同一個效果到底是x1比x2大造成的，還是x2比x1大造成的。

Initially, these approaches compute two predictor variables into a single score, which reduces the available information. For this reason, the difference scores confuse the effects of each of the component measures on the result. The difference scores do not tell us the extent to which each of the component measures contributes to the outcome variable

所以說這個想法就不好，不能說不對哈，只能說不好。

此時最正確的方法就是使用多項式迴歸：

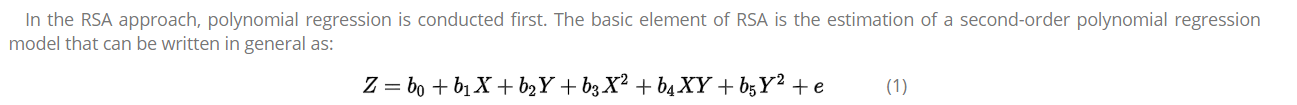
上面的式子中xy為兩個自變數，Z是因變數，式子中還有xy的2次項，對於這麼一個式子我們可以對其圖形化表達

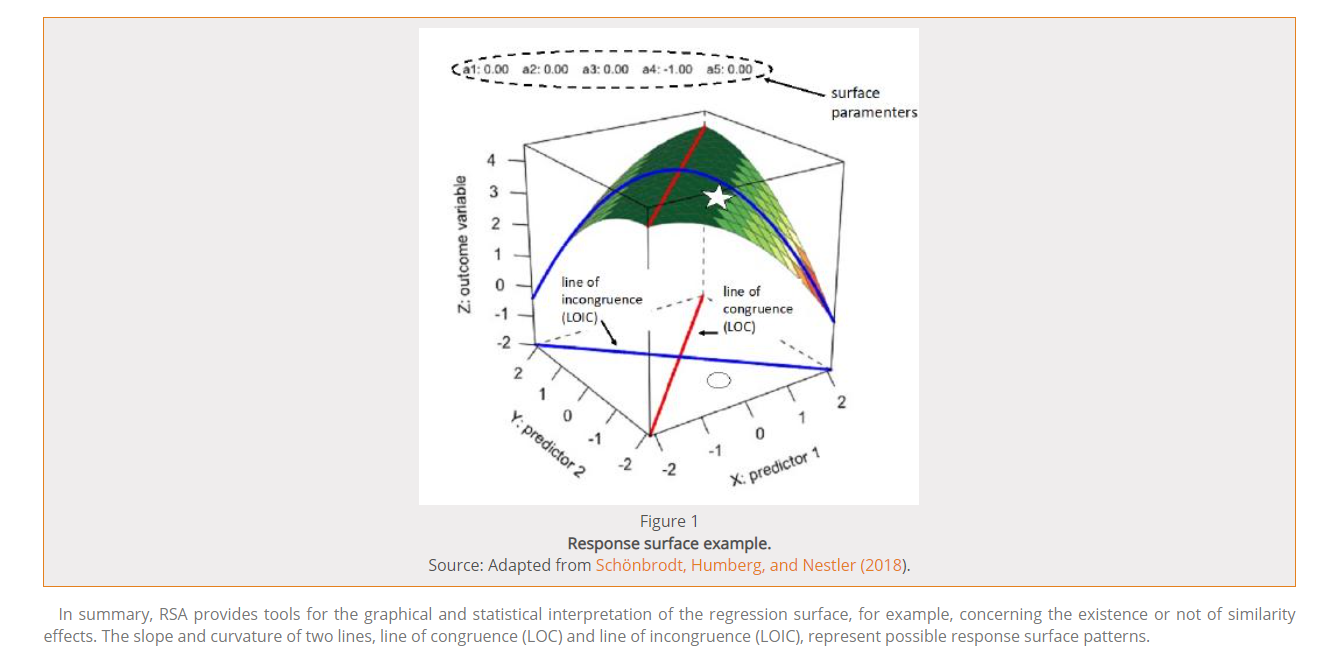
圖中兩個自變數在xy軸上，因變數或者叫模型的響應值在z軸上，這樣所有xy組合取值對應的模型響應值便成了一個曲面，叫做響應面。

比如對應特定的xy在底面對應的圈圈，其對應的Z值就是響應面上的星星。

看圖的時候有兩條線值得我們格外關注：圖中的一致性線Line of congruence (LOC)和不一致線Line of incongruence (LOIC)

• 一致性線

一致性線就是所有xy相等的點組成的線，就是xy平面上的一條45°線，這條線對應的響應面就表示一致性變化時z值的變化。在圖中就是上圖中的紅線對應的響應面，可以看到在xy一致的時候Z值始終是最大的。

• 不一致線

不一致線就是所有xy互為相反數的點組成的直線，就是xy平面上和一致性線垂直的線，在上圖中就是xy平面上的藍色的線，可以看到xy的差距越大，Z的值越低。

通過這麼一種視覺化的表達，我們就可以非常容易的知曉xy所有變化情況下，Z的具體變化情況。

並且結合多項式模型的係數情況我們還可以對相應的假設進行檢驗

我們回到一致性線所對應的響應面，在這個響應面上x=y，Z的表示式就成了一個二次函數：

Z = a1X + a2X2，其中a1 = b1 + b2 and a2 = b3 + b4 + b5

係數a2決定了對應的響應面是直線還是曲線，a1就決定了對應的響應面的斜率。

再看不一致線所對應的響應面，在這個響應面上x=-y，Z的表示式也是一個二次函數：

Z = a3X + a4X2，其中a3 = b1-b2 and a4 = b3-b4 + b5

係數a4決定了對應的響應面是直線還是曲線，a3就決定了對應的響應面的斜率

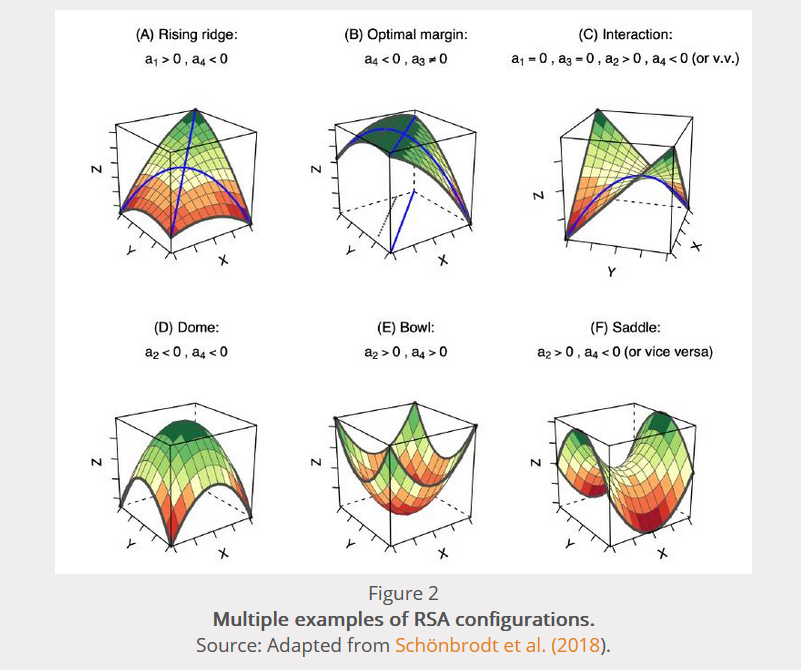
根據係數的不同組合反應在圖中就有響應面的不同的形狀：看下圖，比如a1>0（一致性線對應的Z值為斜率向上的直線），a4<0（非一致性線對應的響應面為開口向下的曲線）的時候對應的圖就是下面A圖；比如a2和a4都<0時兩條線對應的響應面都為開口朝下的曲線，整個響應面的形狀就是下面D圖：等等：

通過上面介紹的係數我們就可以對相應假設進行驗證，接著往下我們來看兩篇實際例文。

一篇文獻名如下：

Bai, Q., Lei, L., Hsueh, F. H., Yu, X., Hu, H., Wang, X., & Wang, P. (2020). Parent-adolescent congruence in phubbing and adolescents’ depressive symptoms: A moderated polynomial regression with response surface analyses. Journal of Affective Disorders, 275, 127-135.

文章做了低頭族這一行為習慣對抑鬱發生的影響，同時考慮了父母低頭和孩子低頭，在形成了多項式迴歸模型後，選取變數進行了響應面分析，主要結果長這樣：

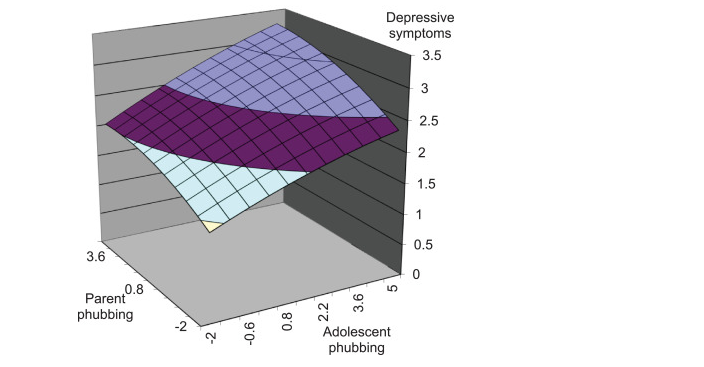
作者把關心的兩個自變數一個是父母低頭，另一個是孩子自己低頭，放在xy軸上；把因變數孩子抑鬱放在z軸上，通過這樣一種圖形化表示就可以看得出來，x和y一致增大的時候和xy變化不一致的時候抑鬱的變化，從而回答研究問題。

結果呈現上作者報告了一致性線的係數和p值，從而回答假設4：

就是一致性線的斜率是顯著的正值，就意味著家長和孩子都是低頭族（一致性的低頭）孩子抑鬱風險會增大。同時還有不一致性線的係數也是同理理解。

作者通過這麼一個分析還檢驗了調節作用，方法部分的原文敘述見下圖，用的方法叫做hierarchical regression analysis：

就是巢狀幾個迴歸，然後比較模型的R方從而資料驅動的角度判斷互動項是不是應該存在。原理在於：加上互動項後R方顯著變大，說明互動項的加入可以顯著地增大模型的解釋力度。

再看一篇管理學領域的文章：

Lee, K., Woo, H. G., & Joshi, K. (2017). Pro-innovation culture, ambidexterity and new product development performance: Polynomial regression and response surface analysis. European Management Journal, 35(2), 249-260.

在驗證下面兩個假設的時候文章使用了響應面分析：

NPD performance will increase as both exploitation and exploration increase simultaneously.

NPD performance will decrease as the imbalance between exploitation and exploration increases in either direction.

依然是探討兩個自變數變化趨勢的一致和不一致問題，作者給了圖和表格來回答研究假設：

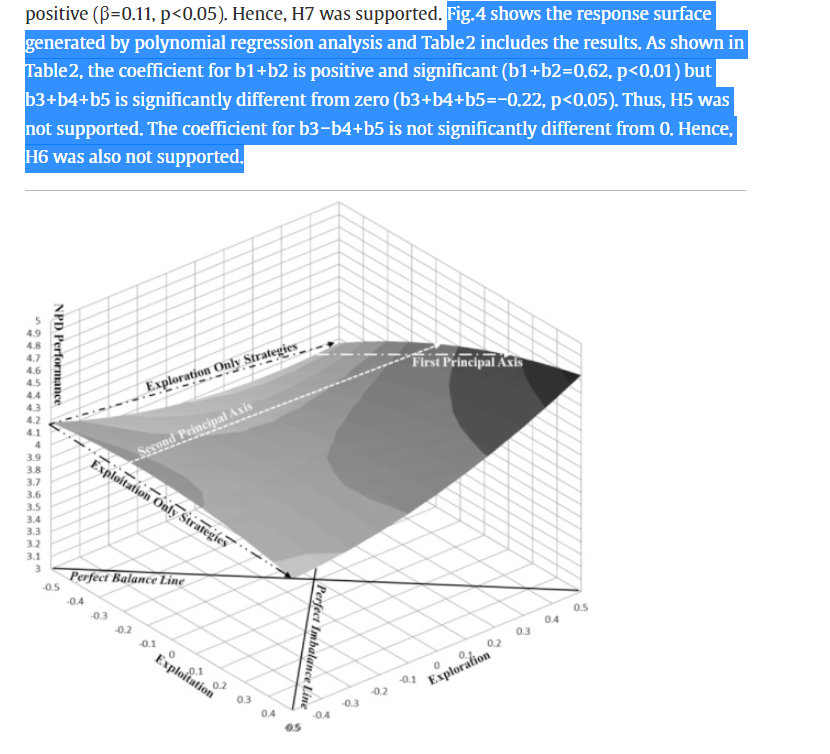
原文中假設5的意思是兩個自變數同時變大的情況下，因變數也會隨之增大，為了驗證這個假設，文章是令將原來的多項式迴歸中的兩個自變數相等，簡化方程後看回歸係數，迴歸方程簡化後就是一個二次函數了，此時滿足假設5的條件就是二次項的係數得為0（二次項得不顯著，不然函數是個曲線，就不滿足假設5因變數一直增長的假設，請回憶初中二次函數的知識點）然後一次項得是負值。

也就是上表中b1+b2得是正的，然後b3+b4+b5得不顯著，因為第二個條件不滿足所以作者得到了假設5不成立的結論。

同理，假設6認為，兩個自變數不一致的情況下，因變數會變小，為了驗證這個假設，文章是令兩個自變數為相反數，此時要滿足假設6的條件就需要，簡化後的方程的一次項係數應該為顯著的負值，二次項應該為0或顯著負值。

也就是上表中b1-b2應該為顯著負值，然後b3-b4+b5應該為0或負值，因為兩個條件都不滿足所以作者得到假設6不成立的結論。

通過這樣的一圖一表，文章就完成了對研究問題的回答。以上就是響應面分析的兩個例文的簡要介紹，詳細寫作請自己扒拉原文瞅瞅。我們接著看做法。

做法步驟

spss是可以做響應面分析的哈，不過我們依然只寫用R的方法，做響應面分析步驟有二：

conceptually RSA is divided into two stages: (a) running a polynomial regression model and (b) using the results of the model to generate a response surface and analyze the importance of the effects

在R中做響應面分析可以用rsm包，第一步是擬合帶有2次項的多項式迴歸，比如我現在有如下資料，x,y,z三個變數

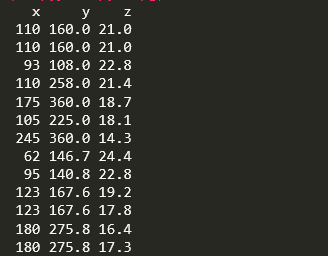
首先我需要跑一個二次多項式迴歸：

rsm(z ~ SO(x, y), data = data)

執行後直接summary上面函數生成的物件即可得到二次多項式的結果

可以看到xy每個項的係數都有展示，我們就是結合這些係數來驗證我們的研究假設。

第二步便是將模型結果通過響應面進行視覺化展示，程式碼如下：

persp (rsm, ~x+y, 
       col = color,main="範例操練",
       xlab=c("關注公眾號","Codewar"),zlab = "範例",
       r=50,d=30,expand=1,box = T,
       #ltheta=10,lphi=99,
       shade=0.1,theta=-15,phi=15,
       #axes=F,
       contour=list(z="bottom"),
       cex.lab=1,
       cex.axis=0.5,
       ticktype="detailed",
       at = xs(rsm))

上面程式碼中rsm為模型物件。執行後即可出響應面圖如下：

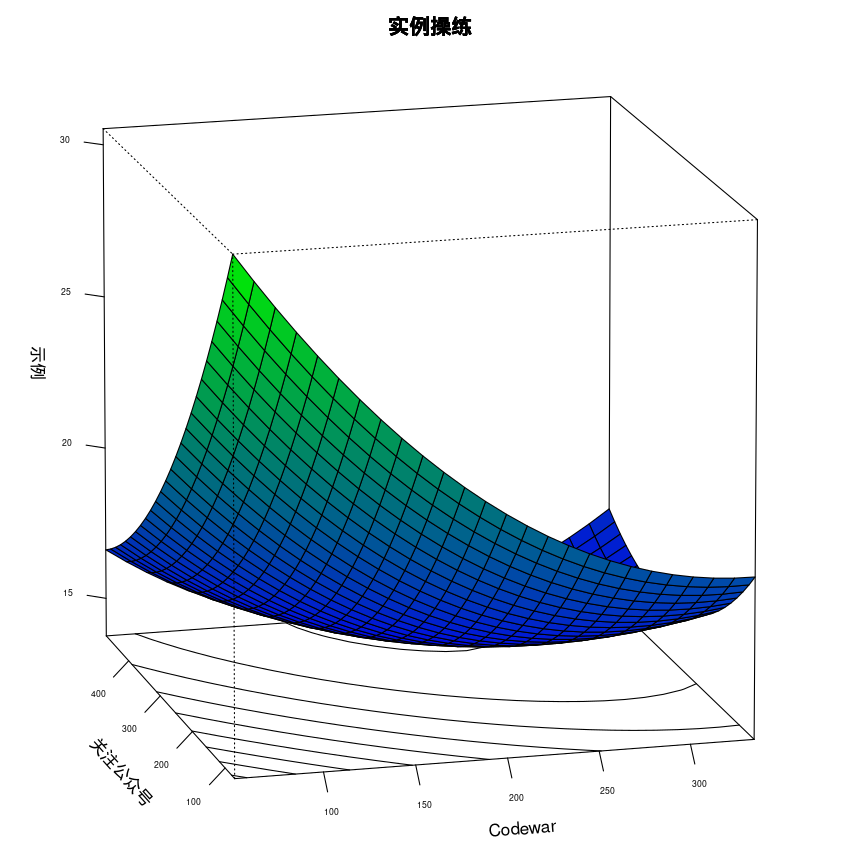
通過上圖就可以很直觀地看到xy不同變化時，z值的對應變化。

到此響應面分析結束。