【學習筆記】博弈論 ---- 非偏博弈
博弈論入門
前言:
本篇按照 Qingyu 在省集講的加入我這個萌新的萌新理解而成。
聽了 Qingyu 的博弈論講解,感覺我之前學過的博弈就是冰山一角。
由於有一些東西沒聽懂,就主要寫寫我聽懂的部分,沒懂得以後再說吧。
所以這篇只是一個入門,關於博弈的一些習題可能會咕咕咕。
平等博弈(非偏博弈):
基礎知識:
幾個基本定義:
- Nimber(即 SG 值),使用 \(*_k\) 代表一堆 Nimber 為 \(k\) 的石子對應的博弈
- 基本的平等博弈的分析技巧:打表 SG 值、轉化為經典模型
- Nim 和:\(*_a + *_b = *_{a \oplus b}\),其中 \(\oplus\) 即按位元互斥或。
在平等博弈中有如下的幾種常見的性質以及技巧:
- 在分析問題時可以使用模仿的思想:
- 在階梯 Nim 遊戲中,可以理解為,先手將石子從偶數位移到奇數位後,後手可以將奇數位的這些石子不動地移動到偶數位,而地面為 \(0\) 為偶數位,也就是可以一直移動直到刪除,那麼偶數位就無用了,將奇數位的石子移動到偶數位就可以理解為刪除
- Nimber 的性質:\(*_a + *_a = 0 \to *_a = -*_a\),也就是我們的插入和刪除本質上是相同的
- 必勝態的後繼狀態一定存在必敗態,必敗態的後繼狀態一定全是必勝態。
Anti-SG 遊戲:
在原始的 sg 遊戲中取最後一個若定義為輸,則其被定義為 anti-sg,其滿足以下性質:
若當局面中所有單遊戲的 SG 值為 \(0\) 則遊戲結束,則先手必勝當且僅當:
-
遊戲的 SG 值不為 \(0\) 且遊戲中某個單一遊戲的 SG 大於 \(1\)
-
遊戲的 SG 值為 \(0\) 且遊戲中沒有單一遊戲的 SG 大於 \(1\)
這個定理證明過於複雜,在我寫的《【學習筆記】博弈論(1)》裡有,可以看看。
Multi-SG 遊戲:
我們定義 Multi-SG 遊戲滿足以下的特徵:
-
在符合拓撲序的前提下,Multi-SG 的每一個後繼狀態均為多個單一的遊戲
-
Multi-SG 遊戲的其他規則與一般 SG 遊戲規則一致。
在這種情況下一個後繼狀態的 SG 值即為多個獨立遊戲的 SG 值的互斥或和。
對於一個二維的遊戲,如果兩個維度相互獨立則可以證明:可以將兩個維度獨立計算,兩個的 Nim 和即遊戲的 SG 值
Nim 積:
我們定義兩個非負整數之間的 \(\otimes\) 運算為 Nim 積運算,其滿足如下的定義式:
並且滿足以下的式子:
Nim 積有交換律、結合律和對 Nim 和的分配律。
為了高效計算 Nim 積,引入 Fermat power 的定義:我們定義形如 \(2^{2^{k}}\) 的數稱為 Fermat power,那麼它有如下的性質:
-
對於 \(n\),若 \(N > n\) 且 \(N\) 為 Fermat power,則 \(n \otimes N = n \times N\)
-
若 \(N\) 為 Fermat power,則 \(N \otimes N = \frac{3}{2}N\)
因此我們就可以利用上述的性質快速計算 Nim 積。
考慮設 \(f(x,y) = x \otimes y\),我們可以考慮按照二進位制每一個單獨考慮,即設 \(g(x,y) = 2^x \otimes 2^y\) 則 \(f(x,y) = \oplus_{x' \in x,y' \in y}\ \ g(x',y')\),這裡定義的 \(x' \in x\) 就是指的 \(x\) 二進位制下 \(x'\) 這一位為 \(1\)。
然後下面就是考慮如果計算 \(2^x \otimes 2^y\) 的情況,也就是求解 \(g(x,y)\),考慮 \(x,y\) 二進位制下的最高位 \(k\):
考慮將 \(x,y\) 按二進位制拆分,從高到低考慮每一位,如果當前位均為 \(0\) 則忽略這一位,下面就是分類討論一下:
若當前位都為 \(1\):設 \(M = 2^{2^k},X = 2^{x - 2^{k}},Y = 2^{y - 2^{k}}\),答案可以如下推導:
若當前位僅有一個為 \(1\):設 \(x\) 這一位為 \(1\),則類似設 \(M = 2^{2^{k}},X = 2^{x - 2^{k}},Y = 2^y\),答案可以如下推導:
遞迴的考慮上述問題,按兩種情況分類之後,可以得到如下的結論:
時間複雜度顯然為 \(O(\log x \log y)\)
程式碼實現如下:
點選檢視程式碼
#define Resolve(i, x) for (int u = (x), i = 0; (1ll << i) <= u; ++ i) if (u >> i & 1)
ll f(ll x, ll y);
ll g(int x, int y) {
if (!x || !y) return 1ll << (x | y);
if (~ tab[x][y]) return tab[x][y];
ll res = 1;
Resolve(i, x ^ y) res <<= (1 << i);
Resolve(i, x & y) res = f(res, 3ll << ((1 << i) - 1));
return tab[x][y] = res;
}
ll f(ll x, ll y) {
if (!x || !y) return 0;
if (x == 1 || y == 1) return max(x, y);
ll res = 0;
Resolve(i, x) Resolve(j, y) res ^= g(i, j);
return res;
}
經典模型:
掌握了這些理論知識,下面就要開始看一些經典的博弈問題了(感覺可能以後會換換順序):
Nim 博弈:
見《【學習筆記】博弈論(1)》
"翻硬幣"遊戲:
下面大概對著 《Game Thoery》的思路說了一下,加一些我自己的萌萌的解釋
首先對"翻硬幣"遊戲進行定義:\(n\) 個硬幣排成一排,每個硬幣可能為正面可能為反面,從左到右按 \(1\) 到 \(n\) 編號,其必須滿足以下的規則
-
對於我們按照規則約束的一次翻硬幣的過程中,最右邊的硬幣必然從正面變成反面
-
定義不能翻的人為輸
在這種定義下其滿足這樣的性質:
當前局面的 SG 值等於每個正面向上的棋子單獨存在時的 SG 值的互斥或和。
例如:\(G(\text{10110}) = G(\text{1}) \oplus G(\text{001}) \oplus G(\text{0001})\)。
所以我們在此類問題中只需要考慮一個棋子的情況,所以在下文的所有型別中在不進行特殊標註的前提下,都預設只有最右邊的棋子為正,其他的為負。
規則約束一:每次只能翻一個硬幣
考慮對於一堆既有正也有反的硬幣,按照上文的定理我們既然每次只能翻一個硬幣,那麼對於任意一個單獨的正的棋子它的 SG 值都為 \(1\),所以當前局面的 SG 值就為正棋子的個數的奇偶性,其中奇數為 \(1\),偶數為 \(0\)。
規則約束二:每次可以翻轉一個或者兩個硬幣(不要求連續)
依舊考慮一堆既有正也有負的棋子,我們將初始編號設為 \(0\),並將每個棋子的 SG 值設為它的編號,則此時就等價於 Nim 遊戲。
(不是很會證明)
規則約束三:每次必須連續翻轉 \(k\) 個棋子
假設 \(k=3\),可以有如下的分析:
當 \(n = 1\),硬幣:正,則先手必輸,此時 \(SG[1] = 0\)
當 \(n = 2\),硬幣:負正,則先手必輸,此時 \(SG[2] = 0\)
當 \(n = 3\),硬幣:負負正,先手翻轉一次後的狀態為:正正負,此時 \(SG[3] = \text{mex}\{0,0\} = 1\)
同理分析可以得到如下表格:
| n | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| SG | 0 | 0 | 1 | 0 | 0 | 1 |
所以其實當 \(k=3\) 時,我們的 SG 值的變化為 \(001001001\cdots\)
所以同理當 \(k \not= 3\) 時,SG 值就為 \(000\cdots001000\cdots001\cdots\)
其中每段中間的 \(0\) 的數量就是 \(k-1\)。
規則約束四:每次翻轉 \(x\) 必須選擇 \(x-1,x-2,x-3\) 中的一個翻轉,除非 \(x\) 小於等於 \(3\)。(Subtraction Games)
當 \(n=1\),硬幣:正,則先手翻轉一次後的狀態為:負,此時 \(SG[1] = \text{mex} \{0\} = 1\)
當 \(n=2\),硬幣:負正,則先手翻轉一次後的狀態為:負負、正負,此時 \(SG[2] = \text{mex} \{0,1\} = 2\)
當 \(n=3\),硬幣:負負正,則先手翻轉一次後的狀態為:負正負、正負負、正正負,此時 \(SG[3] = \text{mex}\{2,1,0\} = 3\)
同理可以得到以下表格:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| SG | 1 | 2 | 3 | 0 | 1 | 2 | 3 |
趨勢是十分明顯的,如果限制不是 \(3\) 而是一些其他的值得到的結果也是類似的。
規則約束五:每次必須翻動兩個硬幣,且這兩個硬幣的距離必須在 \(S = \{1,2,3\}\) 中,硬幣編號從 \(0\) 開始。(Twins 遊戲)
當 \(n=1\),硬幣:正,則先手無法翻動,此時 \(SG[0] = 0\)。
當 \(n=2\),硬幣:負正,則先手翻動一次後的狀態為:正負,此時 \(SG[1] = \text{mex}\{0\} = 1\)
當 \(n=3\),硬幣:負負正,則先手翻動一次後的狀態為:正負負、負正負,此時 \(SG[2] = \text{mex}\{0,1\} = 2\)
同理可得以下表格:
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| SG | 0 | 1 | 2 | 3 | 0 | 1 | 2 |
規則約束六:每次可以翻動一個、兩個或三個硬幣,硬幣編號從 \(0\) 開始。(Mock Turtles 遊戲)
當 \(n=1\),硬幣:正,則先手翻動一次後的狀態為:負,此時 \(SG[0] = \text{mex}\{0\} = 1\)
當 \(n=2\),硬幣:負正,則先手翻動一次後的狀態為:負負、正負,此時 \(SG[1] = \text{mex}\{0,1\} = 2\)
當 \(n=3\),硬幣:負負正,則先手翻動一次後的狀態為:負負負、負正負、正負負、正正負,此時 \(SG[2] = \text{mex}\{0,2,1,3\} = 4\)
同理可得以下表格:
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| SG | 1 | 2 | 4 | 7 | 8 | 11 | 13 | 14 | 16 | 19 |
可以發現值要麼為 \(2\times x\) 要麼為 \(2 \times x + 1\)。
我們此時定義一個非負整數 odious 當且僅當其二進位制下 \(1\) 的個數為奇數,否則則定義為 evil,所以結論如下:
規則約束七:每次可以翻動任意多個連續的棋子,要求至少翻動一個。(Ruler 遊戲)
考慮後繼狀態,如果我們翻動了 \(i\) 個,且總共有 \(n\) 個,則這個後繼狀態的 SG 值為:\(\oplus_{j \in [n-i+1,n-1]}\ \ SG[j]\),需要特別注意的是,翻動 \(1\) 個的後繼狀態的 SG 值為 \(0\),因為此時棋子全部為負。那麼就有如下的式子:
依舊是注意 \(j=1\) 時括號內的值為 \(0\)。
此時打表出來即如下所示:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| SG | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 8 |
很顯然 \(SG[n] = \text{lowbit}(n)\)
巴什博弈:
問題描述:一堆石子有 \(n\) 個,先後手輪流取,一次取 \([1,m]\) 個,無法操作的人為輸.
結論:若 \(n \% (m+1) = 0\) 則先手必敗。
證明:
若 \(n = m + 1\),設先手取 \(x\) 個,則後手一定可以取 \(m + 1 - x\) 個,然後先手必敗。
若 \(n = p(m+1)\),則可以仿照上述的思路,每一次兩人操作都使得 \(n\) 減少 \(m-1\),先手必敗。
若 \(n = p(m+1)+q\),則先手可以一步將局勢變為 \(n = p(m+1)\) 則此時後手必敗。
威佐夫博弈:
問題描述:有兩堆石子個數不一定相同,先後手輪流取,一次可以從一堆中取若干個或者從兩堆中同時取若干個,無法取的人輸。
結論:面對非奇異局勢,則先手必勝,反之後手必勝。
證明:
首先就要定義一下什麼叫做奇異局勢,我們設一個局勢為一個二元組 \((A,B)\) 分別表示兩堆石子的數量,我們定義奇異局勢就是先手必敗的局勢,可以發現奇異局勢有很多的性質。
可以發現,前幾個奇異局勢如下:\((0,0)\)、\((1,2)\)、\((3,5)\)、\((4,7)\)
根據一堆複雜的推導,我們發現奇異局勢一定滿足如下公式:\(A_k = \big\lfloor k \times \dfrac{\sqrt{5} + 1}{2} \big\rfloor,B_k = A_k + k\)
我們就可以通過上述的式子判斷奇異局勢。
奇異局勢有以下的性質:
- 任何自然數都被唯一的包含在一個奇異局勢中
- 任何一個奇異局勢都只能通過一次操作變成非奇異局勢
- 任何一個非奇異局勢都一定可以通過某個操作變為奇異局勢
後面兩條其實就是我們平等博弈的重要性質:必勝態的後繼一定存在必敗態,必敗態的後繼一定均為必勝態。
Fibonacci Nim:
問題描述:
有如下的規則:
- 先手不能在第一次把所有的石子取完
- 之後每一次可選擇的石子數量下界為 \(1\) 上界為上一次取得個數乘 \(2\)。
結論:所有的必敗態構成 Fibonacci 數列
證明就是要引入一個定理:Zeckendorf 定理:任何一個非負整數必然可以分解為不連續的 Fibonacci 數之和。
具體證明就是先通過數學歸納法證明當 \(n\) 為 Fibonacci 數時成立,然後再考慮若 \(n\) 不是則分解之後繼續證明。
具體的證明在這裡:有點複雜,感覺沒啥營養
Green Hackenbush(無向圖刪邊):
Hackenbush 的一般問題描述為:給定一個有根圖,其中地面為根,可以用一條虛線表示,每次可以刪去一條邊以及刪去這條邊後與地面斷開的邊,直到沒有邊與地面相連。
現在是平等博弈章節,僅討論這個遊戲的平等博弈版本,也就是每個玩家在其回合內可以刪除任意的一條邊,在以後我們會稱這種每個玩家都可以刪除的邊為綠邊。
情況一:Bamboo Stalks
可以算是 Green Hackenbush 的引入,問題描述具體為:給定一個具有 \(n\) 條邊的線形圖,其餘規則同上。
具體可以根據下圖來理解這個博弈:

設總共有 \(n\) 條線,其包含的邊數分別為 \(A_1,A_2,A_3,\cdots,A_n\),則該問題等價於 \(N\) 堆石子,每堆石子分別為 \(A_1,A_2,A_3,\cdots,A_n\) 的 Nim 博弈,因為我們進行的操作本質相同。
情況二:Green Hackenbush on Tree
問題描述:給定 \(n\) 棵樹,根連線在地面上,其餘規則同上。
具體可以根據下圖來理解這個博弈:

根據情況一我們將這個遊戲與 Nim 博弈結合了起來,所以其實對於解決此類問就是考慮如何計算對應的 SG 值。
對於這個問題我們要用到一個定理 Colon Principle:對於一個樹上的節點,如果與它連線的路徑都為線形結構,設各個路徑的長度為 \(a_1,a_2,a_3,\cdots,a_n\),則可以直接將這些路徑用長度為 \(\oplus_{i=1}^n a_i\) 的線性結構代替
如下圖所示:

我用紅框標註的點就是每一次選擇將邊變為線性結構的點,看這個圖應該很好理解。
Colon Principle 的證明也是簡單的:就是我們對於原來圖中任意刪除一個邊使得 SG 值產生的影響,在新圖中必然也能做到。(當個感性理解就好)
情況三:Green Hackenbush on general rooted graphs
問題描述:給定一個任意圖,可能有環可能一個聯通塊有多個根連在地面上,其餘規則同上。
具體可以根據下圖來理解這個博弈:
也是要求一下 SG 值,這個時候就有了一個新的定理:
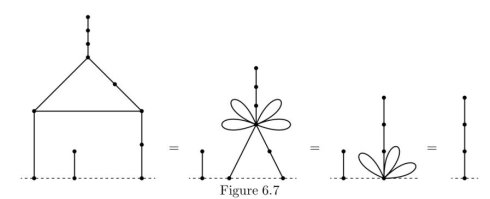
The Fusion Principle:任何一個環內節點都可以縮成一個點而不影響圖的 SG 值。
如下所示:

地面也可以理解為一個節點,所以第一步成立。
將這三個點兩兩縮為一個點,所以第二步成立。
此時每一個環都相當於一個長度為 \(1\) 的線形圖,所以第三步成立。
根據 Colon Principle,所以第四步成立。
進而我們其實可以得到以下的推論:
任意一個奇環都可以縮成一條邊,任意一個偶環都可以縮成一個點。
所以類似的就可以得到下圖這種結論:
小練習
下面就是一些 Exercise,完成這一部分我們的平等博弈就算是完結撒花了
[清華集訓2016]Alice 和 Bob 又在玩遊戲 QOJ4549
問題描述:
有 \(n\) 個節點, \(m\) 條邊(\(0 \le m \le n - 1\)),構成若干棵有根樹,每棵樹的根節點是該連通塊內編號最小的點。
Alice 和 Bob 輪流操作(Alice 先手),每回合選擇一個沒有被刪除的節點 \(x\),將 \(x\) 及其所有祖先全部刪除,不能操作的人輸。
假設 Alice 和 Bob 都足夠聰明,問 Alice 有沒有必勝策略。
\(n \le 10^5\)
問題分析:
一開始的若干棵有根樹相當於子游戲,所以只需要對於每一棵樹單獨求解它的 SG 值,最後互斥或即為所求。
對於單獨一棵樹,我們選擇一個節點刪除之後,相當於把樹再次分成了若干棵樹,也就是相當於一個 Multi-SG 遊戲,所以對於每一個後繼狀態我們只需要遞迴下去繼續求解即可。
其實我們就是要對於每一個點求 \(SG_u\) 表示 \(u\) 子樹內的 SG 值,\(S_u\) 表示刪除 \(u\) 到根的路徑上的點的局面的 SG 的互斥或和。
那麼也就是相當於:\(S_v = S_u \oplus SG_v\),\(SG_u = \text{mex}\{S_v\}(v \in son_u)\)
這樣我們就得到了這個問題的 \(O(n^2)\) 解法,優化就是放到 Trie 樹上維護,不過與博弈論無關就不細說了。
[省選聯考 2023]過河卒 Luogu P9169
問題描述:
有一個 \(n\) 行 \(m\) 列的棋盤。我們用 \((i,j)\) 表示第 \(i\) 行第 \(j\) 列的位置。棋盤上有一些 障礙,還有一個黑棋子和兩個紅棋子。
遊戲的規則是這樣的: 紅方先走,黑方後走,雙方輪流走棋。紅方每次可以選擇一個紅棋子,向棋盤的相鄰一格走一步。具體而言,假設紅方選擇的這個棋子位置在 \((i,j)\),那麼它可以走到 \((i-1,j),(i+1,j),(i,j-1),(i,j+1)\) 中的一個,只要這個目的地在棋盤內且沒有障礙且沒有紅方的另一個棋子。
黑方每次可以將自己的棋子向三個方向之一移動一格。具體地,假設這個黑棋子位置在 \((i,j)\),那麼它可以走到 \((i-1,j),(i,j-1),(i,j+1)\) 這三個格子中的一個,只要這個目的地在棋盤內且沒有障礙。
在一方行動之前,如果發生以下情況之一,則立即結束遊戲,按照如下的規則判斷勝負(列在前面的優先):
-
黑棋子位於第一行。此時黑方勝。
-
黑棋子和其中一個紅棋子在同一個位置上。此時進行上一步移動的玩家勝。
-
當前玩家不能進行任何合法操作。此時對方勝。
現在假設雙方採用最優策略,不會進行不利於自己的移動。也就是說:
- 若存在必勝策略,則會選擇所有必勝策略中,不論對方如何操作,本方後續獲勝所需步數最大值最少的操作。
- 若不存在必勝策略,但存在不論對方如何行動,自己都不會落敗的策略,則會選擇任意一種不敗策略。
- 若不存在不敗策略,則會選擇在所有策略中,不論對方如何操作,對方後續獲勝所需步數最小值最大的操作。
如果在 \(100^{100^{100}}\) 個回合之後仍不能分出勝負,則認為遊戲平局。請求出遊戲結束時雙方一共移動了多少步,或者判斷遊戲平局。
對於所有的資料,保證:\(1 \leq T \leq 10 ; 2 \leq n \leq 10 ; 1 \leq m \leq 10 ; \text{id}\) 等於測試點編號。
問題分析:
感覺解決這個題的關鍵是不要害怕這個題,正常分析性質就好。
一眼我們就能發現 \(n,m\) 超級小,所以我們可以直接 \(dp\) 表示博弈的狀態,並且能直接將三個棋子的位置全部存下。
那麼我們的 \(dp\) 過程其實就是拓撲排序 + 博弈論的一個過程。
這裡用到的博弈論知識就是:必勝態後繼一定存在必敗態,必敗態後繼一定都是必勝態。
根據這個知識我們就能把博弈的狀態表示好了,但是程式碼真的有點難寫。
[SDOI2019]移動金幣 Luogu P5363
問題描述:
Alice和Bob將要進行如下的一場遊戲。二人輪流操作,且Alice先行。
當輪到一個玩家的時候,他可以選擇一枚金幣,並將其向左移動任意多格,且至少移動一格。
金幣不能被移出棋盤,也不能越過其它金幣。
一個 \(1\times n\) 的棋盤上最初擺放有 \(m\) 枚金幣。其中每一枚金幣佔據了一個獨立的格子,任意一個格子內最多隻有一枚金幣。
如果輪到一個玩家的時候他已經無法做出任何有效操作了(顯然這個時候\(m\)枚金幣恰好落在最左側的\(m\)個格子中),則被判定為輸家。已經知道Alice和Bob都是極致聰明的人,他們在任何局面下總能做出最優的操作。那麼有多少初始狀態能保證Alice必勝呢?
\(1\le n\le 150000\)且\(1\le m\le 50\)。
問題分析:
考慮我們一次移動其實相當於將它與其前面的棋子的空格移動到了它與其後面棋子的空格位置,那麼我們如果將棋子間的距離視為石子數量,這個問題就相當於一個階梯 Nim 遊戲。
階梯 Nim 的結論就是如果奇數位置的石子的互斥或和不為 \(0\) 則先手必敗,但是不為 \(0\) 顯然不如為 \(0\) 好限制,所以 \(dp\) 出為 \(0\) 的方案數最後用總數減一下就好了。
總數就是一個簡單的組合數。