演演算法學習筆記(23): 馬爾可夫鏈中的期望問題
馬爾可夫鏈中的期望問題
這個問題是我在做 [ZJOI2013] 拋硬幣 - 洛谷 這道題的時候瞭解的一個概念。
在網上也只找到了一篇相關的內容:# 馬爾可夫鏈中的期望問題
故在這裡來分享一下其中的期望問題。
馬爾可夫鏈
定義:馬爾科夫鏈為狀態空間中經過從一個狀態到另一個狀態的轉換的隨機過程。該過程要求具備「無記憶性」,也就是說當前狀態的概率僅與上一個狀態相關。
數學定義:假定我們的序列狀態為 \(\dots, X_{t-2}, X_{t-1}, X_t, X_{t+1}, X_{t+2}, \dots\),那麼在 \(X_{t+1}\)
時刻的狀態的條件概率僅依賴於前一刻的狀態 \(X_t\),即:
既然某一時刻狀態轉移的概率只依賴於它的前一個狀態 ,那麼我們只要能求出系統中任意兩個狀態之間的轉換概率,這個馬爾科夫鏈的模型就定了。
概率轉移矩陣
通過馬爾科夫鏈的模型轉換,我們可以將事件的狀態轉換成概率矩陣 (又稱狀態分佈矩陣 ),如下例:
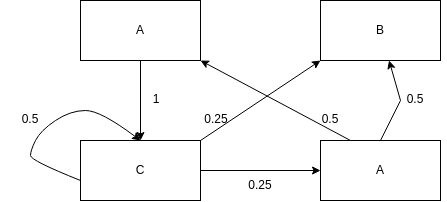
其中線上的數位表示是狀態轉移到另一狀態的概率
額,右下角的應該是D,不想改圖了……
那麼我們可以構造出如下矩陣:
假定我們初始狀態為 \(A\),於是狀態矩陣可以定義為
那麼經過 \(k\) 次轉移後的概率分佈是什麼?
例如 \(k = 4\) 時
通過
numpy計算:s = np.array([[1], [0], [0], [0]]) P = np.array([ [0, 0, 0, 0.5], [0, 0, 0.25, 0.5], [1, 0, 0.5, 0], [0, 0, 0.25, 0] ]) i, n = 0, 4 while i < n: s = P.dot(s) i = i + 1 print(s)
轉移矩陣的修訂
如果我們到達了某一個點就結束了整個過程,那麼我們需要對狀態轉移做一定的更改:
呃,這部分對於本文似乎有一點偏題了……請適當略過
我們新增了一個節點,將所有轉移到 \(B\) 的狀態轉移為最終狀態,也就是對於 \(B\) 的狀態累計求和。
於是新的矩陣成為:
s = np.array([[1], [0], [0], [0], [0]])
P = np.array([
[0, 0, 0, 0.5, 0],
[0, 0, 0.25, 0.5, 0],
[1, 0, 0.5, 0, 0],
[0, 0, 0.25, 0, 0],
[0, 1, 0, 0, 1]
])
最終 \(S_k = P^kS\) 就是積累後的概率矩陣。
狀態中的期望
我們關注的是到達狀態 \(B\) 所需要的平均轉移次數,所以我們把隨機變數 \(X\) 看作到達目標狀態所需要的步數。
根據變數期望的定義可得:
那麼現在的問題就變為了求 \(P(X = k)\)。
根據上文,\(P(X = k) = [B]S_k = [B]P^kS\),也就是取 \(S_k\) 與 \(B\) 相關的那一項。
或許我們可以求得 \([B]S_k\) 的通項(一個多項式?)從而求得期望。
在頂端連結的文章中提到:
事實上,我們可以計算轉移矩陣的 \(n\) 次方,即得到各元素關於 \(n\) 的表示式.
由於我沒有學過線性代數,所以我就不在本文中展開。
而是採用第二種方法:期望線性方程組
期望線性方程組
顯然至少目前對我而言,求通項的方法不可行,所以我們需要利用另外一種方法。
我們仍然求從 \(A\) 轉移到 \(B\) 所需要的平均轉移次數。
那麼我們不妨設 \(E_i\) 表示從狀態 \(i\) 轉移到 \(B\) 所需要的期望次數,\(p_{ji}\) 表示從狀態 \(j\) 從 \(i\) 轉移來的概率。
那麼有:
也就是說 \(E_i\) 等於 \(i\) 可以直接轉移到的狀態的期望乘上轉移的概率的和再加上 \(1\)(轉移的代價,1步)
以上文中例子為例,可以列出:
而特殊的,\(E_B = 0\),因為已經到達目標了
而可以解出 \(E_A = 4\)。
也就是說,從 \(A\) 轉移到 \(B\) 的期望步數是 \(4\)。
方程矩陣化
如果我們把列出來的方程看作矩陣,那麼可以得到:
P = np.array([
[0-1, 0, 1, 0],
[0, 0-1, 0, 0],
[0, 0.25, 0.5-1, 0.25],
[0.5, 0.5, 0, 0-1]
])
似乎是我原本概率轉移矩陣有問題?
也就是原概率矩陣的轉置矩陣再在對角線上全部減一。
或者可以表示為
而我們最終求解的方程為:
利用死去的高斯消元即可。
例題
在題解區中全是某種奇怪的 DP 設計。所以這裡來講述一下利用本文中的方法求解的方法。
最開始的模型轉化我們就省略了……
我們設 \(E_i\) 表示從剩下 \(i\) 個地方沒有按下到全部按下的期望步數。
根據題目,我們有:
並且由於最優限制:
所以我們可以輕易的利用高斯消元求解……但是很明顯,這是不現實的……考慮這個矩陣是一個稀疏矩陣,而且每一個方程是隻與臨近對角線的 3 個元素相關,所以我們可以輕易的將空間優化到 \(O(3n)\)。
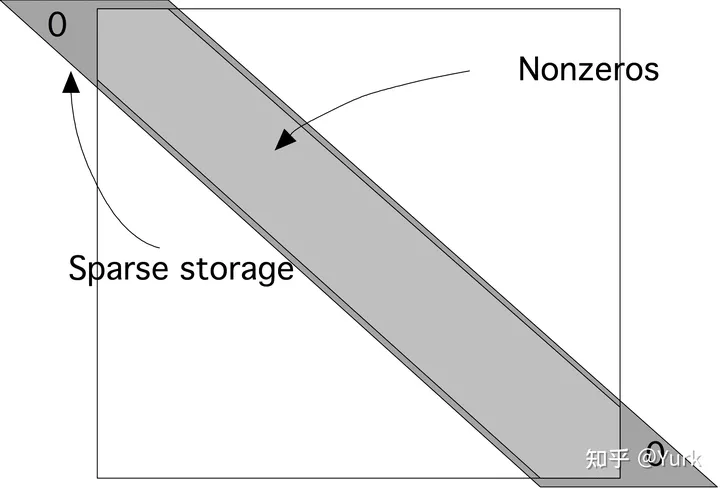
參考至知乎:# 數值線性代數|LU分解與稀疏矩陣
於是我們可以 旋轉 一下,只儲存非0的元素
接下來我們只需要參考 Guass-Jordan 消元法(先從上到下消下三角,再從下到上消上三角)。那麼複雜度成功的也被我們降到了 \(O(n)\)。只是常數有點小大……
作者有話說
其實本文講述的方法存在很大的侷限性,尤其的求解的過程,很容易就變成了 \(O(n^3)\)。
不過似乎建模的過程還是蠻簡單的?
在求期望的問題中,這不失為一個思考的方向。有些時候,可以通過題目相關的特殊性質進行優化,使得複雜度降低。
可是毒瘤出題人們……還是看每道題的正解吧,或許終將有一天,這個方法可以被一種通法優化到 \(O(n^2)\) 呢?