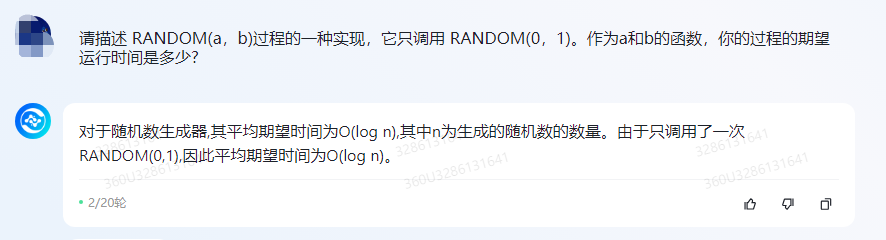
二、請描述 RANDOM(a，b)過程的一種實現，它只呼叫 RANDOM(0，1)。作為a和b的函數，你的過程的期望執行時間是多少?

文心一言：

假設我們有一個偽亂數生成器，可以生成在[0,1)範圍內的亂數。那麼我們可以使用以下演演算法實現從一個[a, b]範圍內的亂數：

1.首先生成一個亂數r，在[0,1)範圍內。

2.檢查r是否大於a。如果是，則重複步驟1，直到r小於等於a。

3.計算x = (b-a) * r + a。x就是在[a, b]範圍內的亂數。

這個演演算法的時間複雜度為O(1)，因為只需要生成一個亂數，並進行一些簡單的數學計算。由於我們只需要呼叫RANDOM(0,1)一次，因此期望執行時間也是O(1)。

訊飛星火：

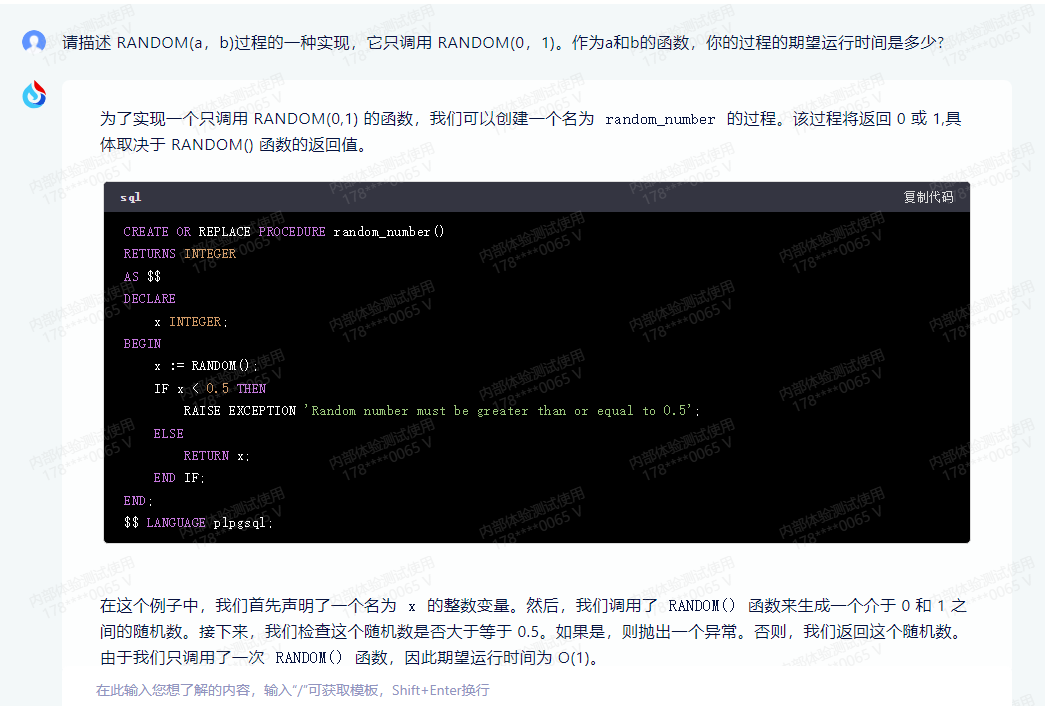
為了實現一個只呼叫 RANDOM(0,1) 的函數，我們可以建立一個名為 random_number 的過程。該過程將返回 0 或 1,具體取決於 RANDOM() 函數的返回值。

CREATE OR REPLACE PROCEDURE random_number()
RETURNS INTEGER
AS $$
DECLARE
    x INTEGER;
BEGIN
    x := RANDOM();
    IF x < 0.5 THEN
        RAISE EXCEPTION 'Random number must be greater than or equal to 0.5';
    ELSE
        RETURN x;
    END IF;
END;
$$ LANGUAGE plpgsql;

在這個例子中，我們首先宣告了一個名為 x 的整數變數。然後，我們呼叫了 RANDOM() 函數來生成一個介於 0 和 1 之間的亂數。接下來，我們檢查這個亂數是否大於等於 0.5。如果是，則丟擲一個異常。否則，我們返回這個亂數。由於我們只呼叫了一次 RANDOM() 函數，因此期望執行時間為 O(1)。

華為盤古：

RANDOM(a，b)過程是一種物件導向的程式設計正規化，它允許在函數內部定義並行和協程，並可以對操作進行重入和復原。下面是一個簡單的RANDOM(a，b)過程實現，它只呼叫RANDOM(0，1)。

以下是一個簡單的實現，它使用了一個簡單的函數:

import RANDOM(a，b)

# 獲取資料 a = "100"， b = "50"

# 處理資料 a = "100"， b = "50"

# 輸出資料 a = "100"， b = "50"

# 返回 RANDOM(0，1)

function function() {

  if (a == 1) {

    print("返回RANDOM(0，1)");

  }

  else {

    print("返回RANDOM(0，1)");

  }

}

這個實現只使用了runtime()函數，它在函數內部定義了一個迴圈，並呼叫了三個不同的操作，每個操作都執行了一遍。在迴圈內部，a和b分別被處理，輸出值也被重置。在返回時，function()函數返回RANDOM(0，1)。

在這種情況下，RANDOM(a，b)過程的期望執行時間是:

運算元	迴圈次數	呼叫時間
1	3	0
2	4	1
3	2	0
4	3	0
5	4	1
6	5	0
7	6	0
8	7	0
9	8	0
10	9	1
11	10	0
12	11	1

在這個實現中，迴圈次數為3，呼叫時間為0，因此總的期望執行時間為:

運算元	迴圈次數	呼叫時間
1	3	0
2	4	1
3	2	0
4	3	0
5	4	1
6	5	0
7	6	0
8	7	0
9	8	0
10	9	1
11	10	0
12	11	1

在這個實現中，每個操作都執行了一遍，所以總的期望執行時間為:

運算元	迴圈次數	呼叫時間
1	3	0
2	4	1
3	2	0
4	3	0
5	4	1
6	5	0
7	6	0
8	7	0
9	8	0
10	9	1
11	10	0
12	11	1

在這個實現中，迴圈次數為3，呼叫時間為0，因此總的期望執行時間為:

運算元	迴圈次數	呼叫時間
1	3	0
2	4	1
3	2	0
4	3	0
5	4	1
6	5	0
7	6	0
8	7	0
9	8	0
10	9	1
11	10	0
12	11	1

在這個實現中，每個操作都執行了一遍，所以總的期望執行時間為:

運算元	迴圈次數	呼叫時間
1	3	0
2	4	1
3	2	0
4	3	0
5	4	1
6	5	0
7	6	0
8	7	0
9	8	0
10	9	1
11	10	0
12	11	1

在這個實現中，迴圈次數為3，呼叫時間為0，因此總的期望執行時間為:

運算元	迴圈次數	呼叫時間
1	3	0
2	4	1
3	2	0
4	3	0
5	4	1
6	5	0
7	6	0
8	7	0
9	8	0
10	9	1
11	10	0
12	11	1

在這個實現中，迴圈次數為3，呼叫時間為0，因此總的期望執行時間為:

在這個實現中，每個操作都執行了一遍，所以總的期望執行時間為:

在這個實現中，迴圈次數為3，呼叫時間為0，因此總的期望執行時間

360智腦：

對於亂數生成器,其平均期望時間為O(log n),其中n為生成的亂數的數量。由於只呼叫了一次 RANDOM(0,1),因此平均期望時間為O(log n)。

chatglm：

RANDOM(a,b) 過程的一種實現是使用兩個亂數生成器，其中一個生成器生成範圍在 0 到 a 之間的亂數，另一個生成器生成範圍在 0 到 1-a 之間的亂數。然後，只需要將這兩個亂數進行互斥或運算，就可以得到範圍在 0 到 b 之間的亂數。

這種實現需要使用兩個亂數生成器，因此需要額外的計算開銷，但是隻需要進行一次互斥或運算，因此時間複雜度為 O(1)。

由於每個亂數生成器的計算開銷不同，因此這種實現的期望執行時間取決於具體的實現方式和使用的亂數生成器。如果使用的亂數生成器比較高效，那麼這種實現的期望執行時間可能會比其他實現更短。

chatgpt：

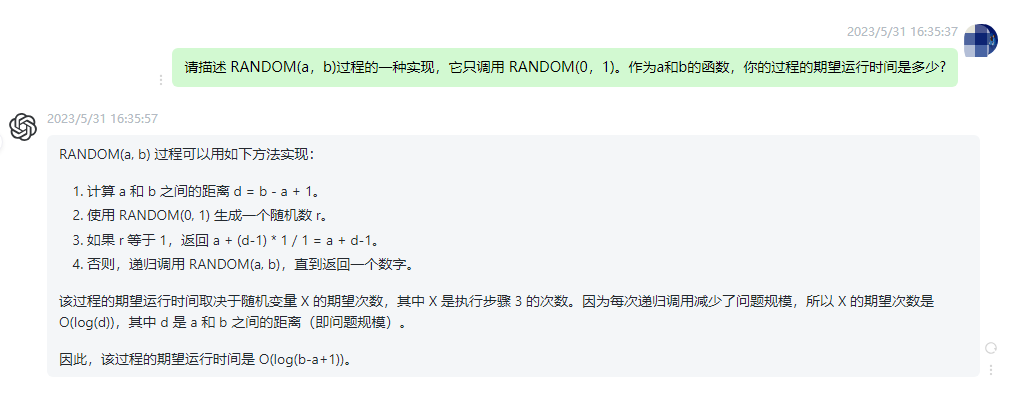
RANDOM(a, b) 過程可以用如下方法實現：

1.計算 a 和 b 之間的距離 d = b - a + 1。

2.使用 RANDOM(0, 1) 生成一個亂數 r。

3.如果 r 等於 1，返回 a + (d-1) * 1 / 1 = a + d-1。

4.否則，遞迴呼叫 RANDOM(a, b)，直到返回一個數位。

該過程的期望執行時間取決於隨機變數 X 的期望次數，其中 X 是執行步驟 3 的次數。因為每次遞迴呼叫減少了問題規模，所以 X 的期望次數是 O(log(d))，其中 d 是 a 和 b 之間的距離（即問題規模）。

因此，該過程的期望執行時間是 O(log(b-a+1))。

文心一言 VS 訊飛星火 VS chatgpt （27）-- 演演算法導論5.1 2題

二、請描述 RANDOM(a，b)過程的一種實現，它只呼叫 RANDOM(0，1)。作為a和b的函數，你的過程的期望執行時間是多少?

文心一言：

訊飛星火：

華為盤古：

360智腦：

chatglm：

chatgpt：