導言：

在計算機發明之初是為了計算，所以叫計算機，對我們給定的一個算式，然後給定的一套規則 加，減，乘，除，等，它就可以自己進行計算了，然後返回一個結果給我們

對於一般的算式 ： 2+3+4 很顯然，從左往右依次掃描，依次相加很簡單的計算出來，因為它們是同級運算，可以很簡單的做到

但是，常見的運算不只是 加法，還有乘除等，它們的優先順序都是要高於加法的，如： 3+6*4/9  ，如果依次掃描，很顯然6和4的乘法優先順序更高，不能先3和6進行加法

當然，有問題的提出就有問題的解決：可以使用字尾表示式和棧結合來應對複雜的計算

一.簡述棧

什麼是棧？

棧 (Stack)是作業系統在建立某個程序時或者執行緒（在支援多執行緒的作業系統中是執行緒）為這個執行緒建立的儲存區域，該區域具有FILO的特性，在編譯的時候可以指定需要的Stack的大小

棧的特點：先進後出 ，即Frist IN Last Out（FILO）

棧這種資料結構就特別適合解決導言提出來的那種問題，對於複雜的計算，算式中帶有優先順序的符號，我們可以使用棧儲存字尾表示式來計算

既然要用到字尾表示式，那麼我們就需要把我們熟知的中綴表示式轉換為字尾表示式才能計算

中綴表示式轉字尾表示式

 我們這裡使用的中綴表示式轉字尾表示式的方法是，補填括號，如果運算有括號的部分就不需要自己新增了，要是無括號就需要新增

差不多有幾個符號，最後填完括號後就是有幾個括號，符號數和括號數對應

然後把符號移動到對應的括號外面，字首和字尾表示式都是這樣的，自己可以試試轉換字首表示式

最後要注意的就是，前字尾表示式是沒有括號的，所以最後一步是去括號（即使中綴表示式自帶的括號一樣去掉）

棧和字尾表示式的結合計算

棧在這裡是扮演的儲存角色，我們在計算的時候會從左往右的依次進行入棧操作，是數位就入棧，是運運算元號我們就需要從棧頂拿出兩個元素計算，

但是記住，是有順序的，棧頂的元素放右邊，後面出來的元素放左邊，符號放中間就可以計算了

棧的特點是先進的後出，後進的先出，不存在在棧中間的資料先出來的情況，所以依次出棧就能保證資料運算時邏輯順序不會發生改變

我們接下來簡單舉例來看看這個運算：

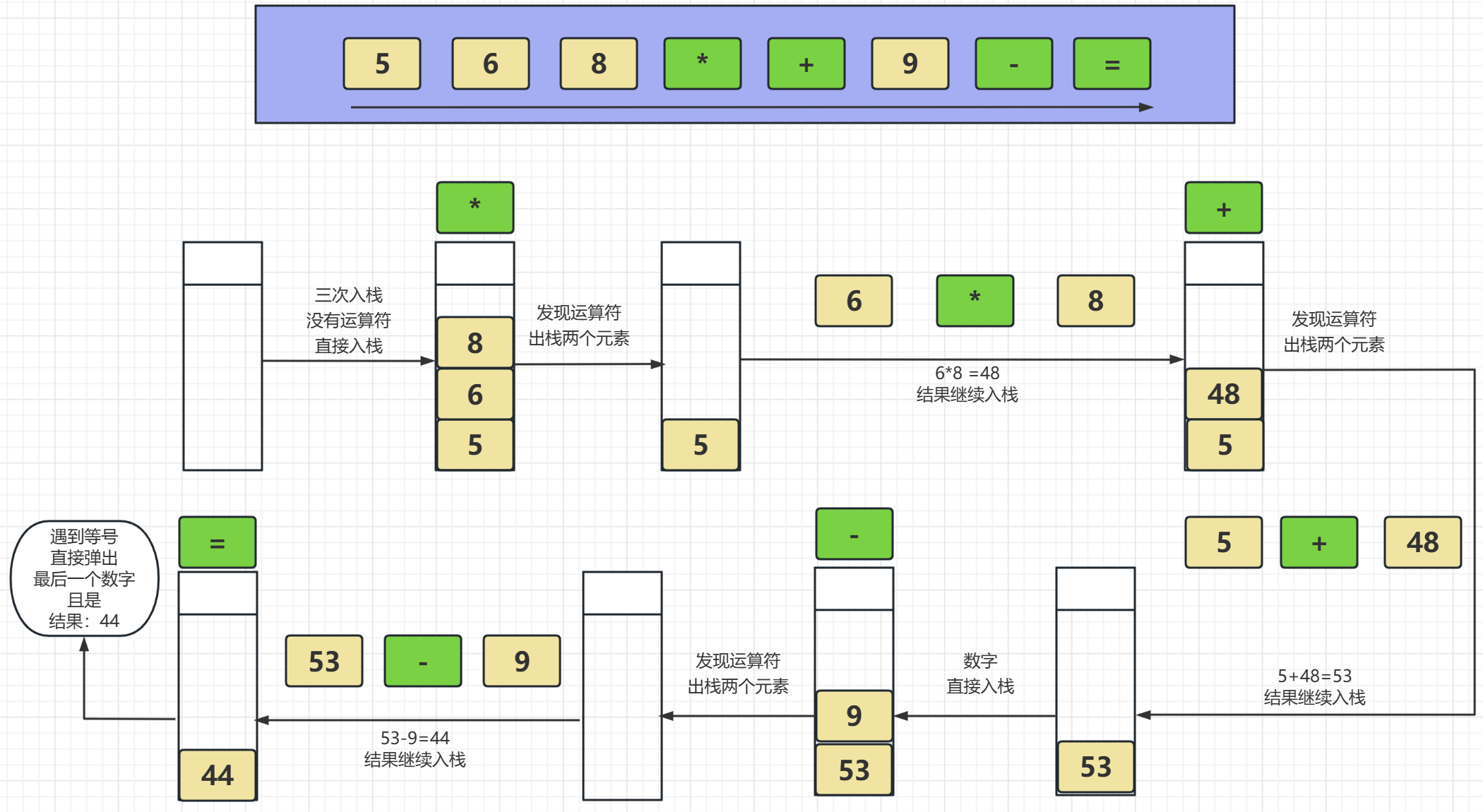
 這就是我們使用棧結構來解決的導言中的比較複雜運算，這裡我們就能很明顯的知道棧的結構特點

棧結構使用最多的還是計算機底層的運算，比如，作業系統的中斷系統中，作業系統做的斷點記錄是棧結構儲存的，還有函數和主函數的呼叫方式，遞迴的實現，都是棧機制

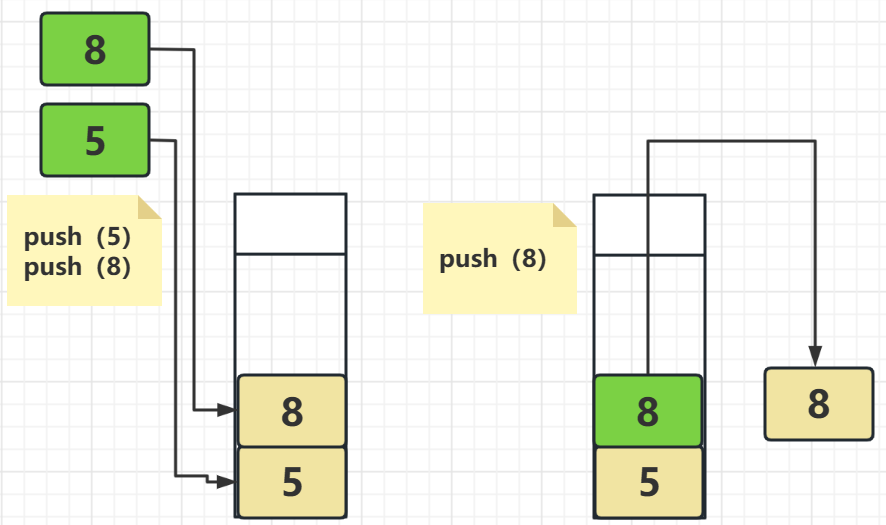
對應的棧操作就兩個：push （入棧），pop（入棧）

不管是出棧還是入棧它們都是原子操作，可以交叉的使用邊出棧邊入棧，也可以邊入棧邊出棧，但是在宏觀上它們一定是有序的，不會有棧頂元素未出棧，棧底元素已出棧的情況

 二.棧的順序儲存實現

 第一種：基於結構體陣列實現

棧的順序儲存通常是一個陣列和一個記錄棧頂元素的變數實現的

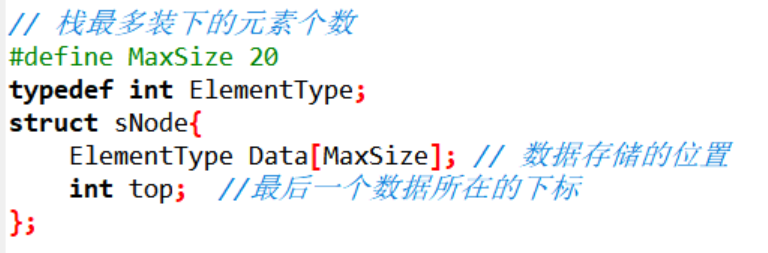
 這裡我們使用的是int型陣列，儲存整型資料

top就是我們有資料陣列的最大下標

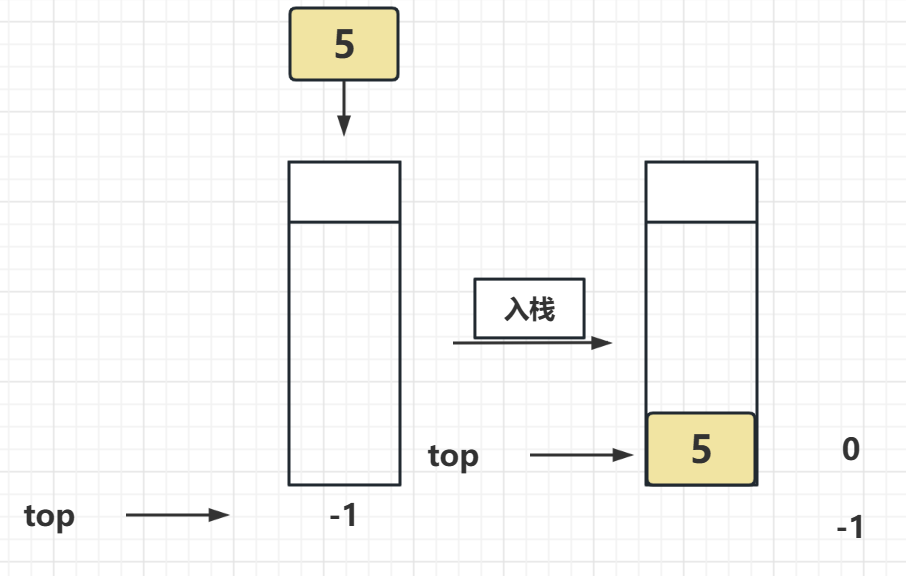
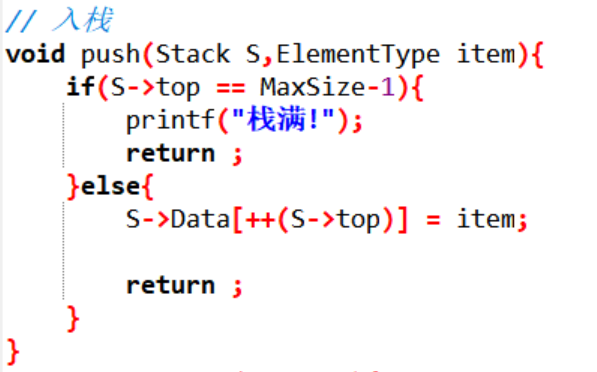
 入棧的時候需要檢查一下我們的棧是否為滿的，如果不是滿地還有空間那麼就可以入棧，入棧的時候由於我們選用的陣列存放，所以只需要把下標後移一個就夠了

然後還要對記錄棧頂的元素加一，這裡程式碼中我們其實是兩步一起做了的

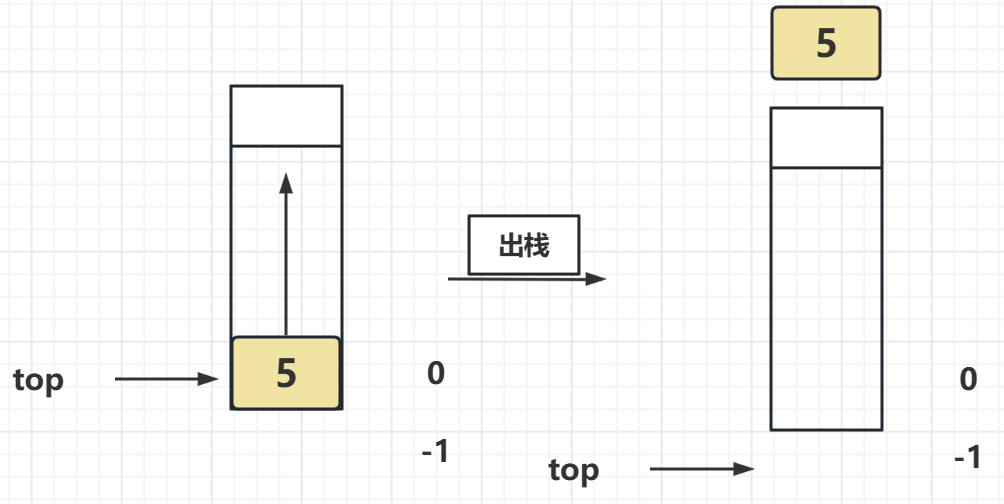
 我們在出戰的時候是有返回值的，一定要記得型別要和入棧的資料型別匹配上

然後就是出棧也需要判斷棧是不是還有元素，沒有就是出不了棧的

出棧完成了以後也需要把記錄棧頂元素的變數減一

利用一個陣列實現兩個棧

 這是一個經典的棧空間劃分問題，我們在拿到問題之後可能很多人都想到的是對半分，一半陣列構成一個棧，理論上可以，但是實際上的開發不行，

因為兩個棧的進入順序其實是不一樣的，那麼就有可能會導致有一個棧已經滿了，另外的一個棧還有大量空間，為了充分利用陣列空間，對半分劃分兩個棧肯定是不合理的

後來我們想到可以使用陣列的第一元素和最後一個元素作為兩個棧的棧底，然後都向中間靠來存放資料，不在是對半分，當兩個棧的棧頂指標相遇的時候就是棧滿的時候

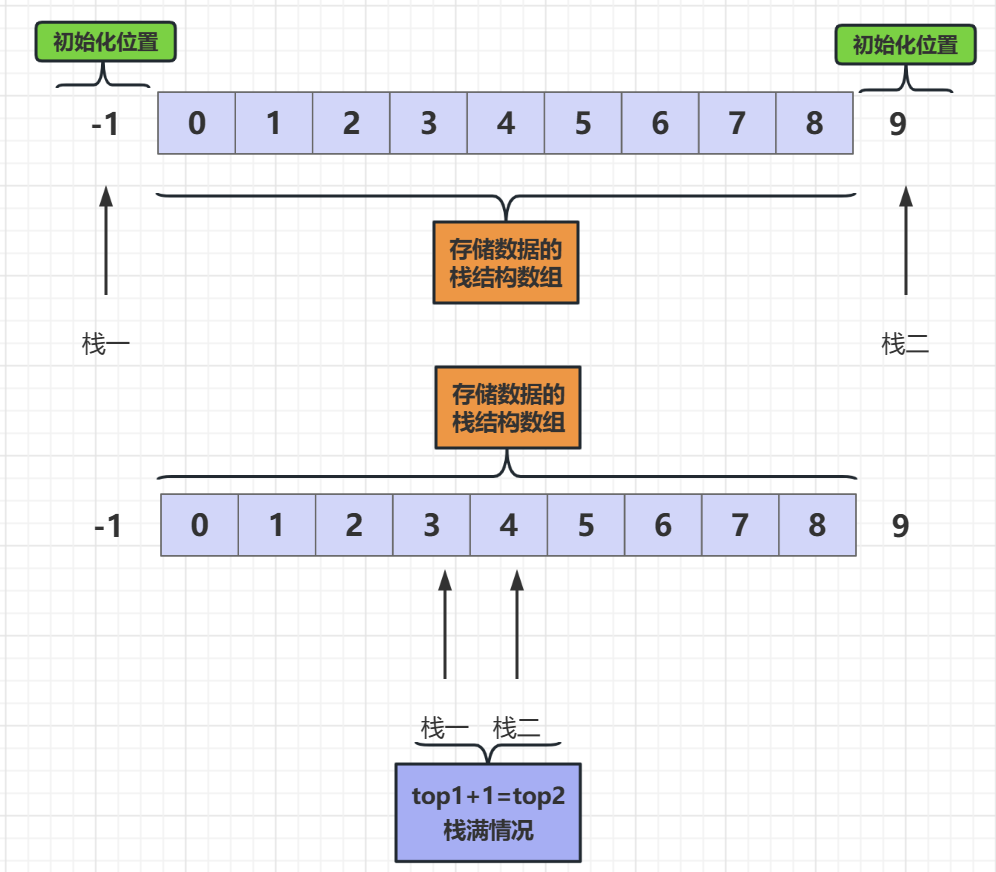
上面就是使用一個陣列實現雙棧的虛擬碼，主要是多了一個tag標記，它的意思是用來選擇要操作那個棧的，我們現在不是有了兩個棧嘛

包括入棧和出棧都要選擇，如果選擇錯了很顯然拿不到我們想要的結果的

使用這種方式構建的雙棧有很高的利用率，不存在有內碎片的情況。 

 第二種：基於鏈式儲存實現

棧的鏈式儲存其實就是一個單連結串列，叫做鏈棧，插入和刪除只能在棧頂實現，那麼連結串列的top指標指向那一頭呢？

我們可以先構造從連結串列的尾部開始做 top指標，插入的時候就在尾部連線連結串列的新結點，但是刪除就有問題了，我們知道連結串列實現的棧是單連結串列它是沒有回頭指標的

也就是說，它只能找到它的下一個結點，但是找不到它的上一個結點，單連結串列有 Next指標，但是沒有 last指標，在刪除的時候肯定要回到上一個結點做尾結點，所以連結串列的尾部被pass掉

再來看看使用連結串列的頭部做top指標，每新來的結點都直接連線到已有的連結串列的後面，可以實現，刪除一個結點也就是頭部結點的next不需要了，連線到下下個結點去，可以實現

所以我們選用頭部結點來做top指標，這裡我們需要注意的是我們要專門構造一個頭部結點，它不存放資料，只用來連線新資料和刪除資料，它不管怎麼更改始終是連結串列的第一個結點，使用這個結點來做 top指標

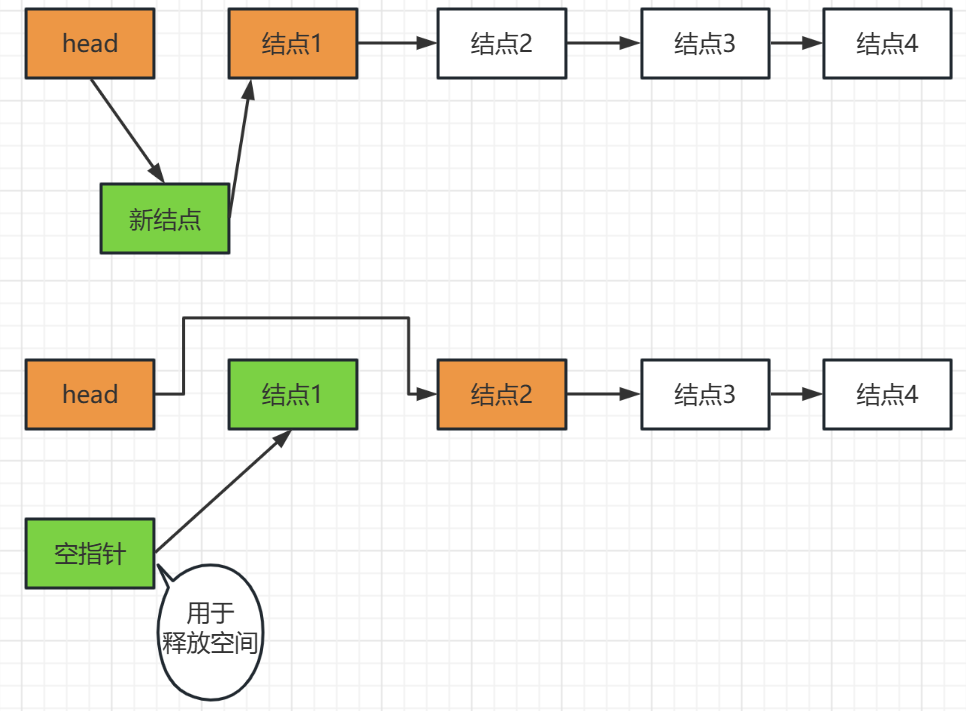
 這裡的head頭結點就可以充當top指標

我們再來看看對連結串列結構體的定義，由於連結串列是動態申請，故而沒有固定大小

 從結構體種我們可以看到，有裝資料的Data型別，還有一個結構體指標，指向的是下一個結構體，利用連結串列來做棧結構首先要申請一個頭結點用於做top指標，這一步也可以叫初始化，

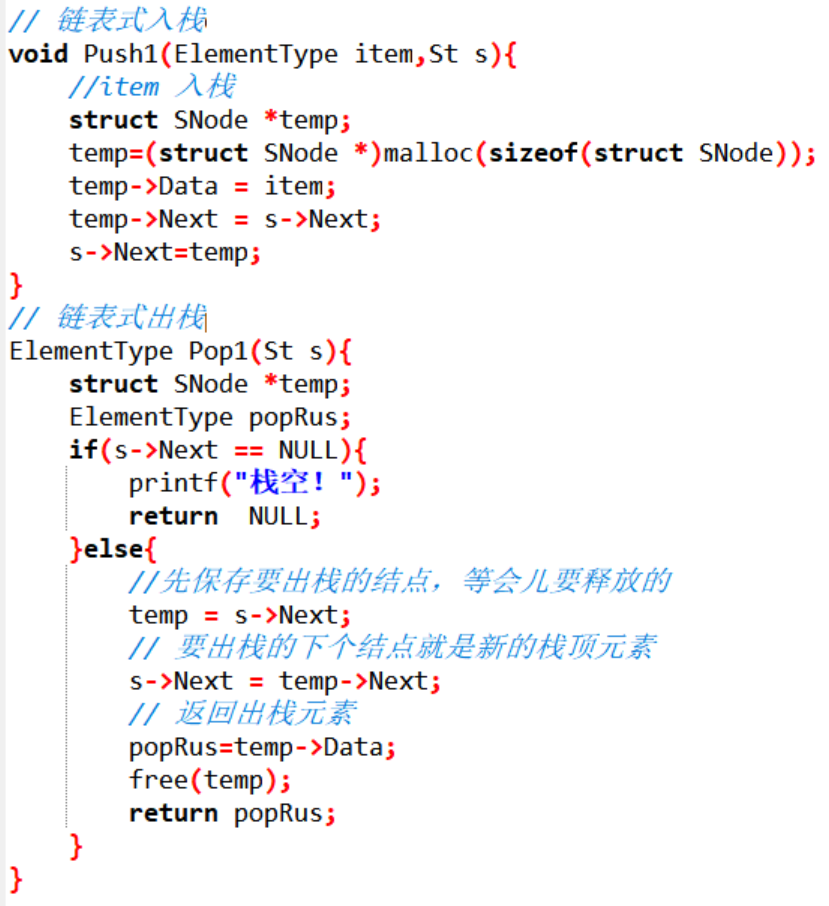
 這裡式虛擬碼實現的鏈式棧結構實現入棧和出棧

入棧的時候要注意每次申請一個新的結點，連結串列的插入實際上是結點的插入，結點上帶了資料和下一個結點的位置

因為鏈式儲存，它的大小是在不斷地申請中產生的所以它是沒有棧滿這個問題的，可以說只要作業系統給你多少記憶體，你可以一直申請到撐爆它。

然後就是出棧，出棧是需要檢查一下有沒有結點的，可能沒有插入，在出棧的時候需要釋放剛剛的記憶體，所以需要一個指標還沒執行斷鏈的時候就指向它

等斷鏈以後，資料也備份到返回的臨時變數了，就可以釋放出棧元素原來所佔用的記憶體了，有申請有釋放，主打一個規範

 入棧圖示：

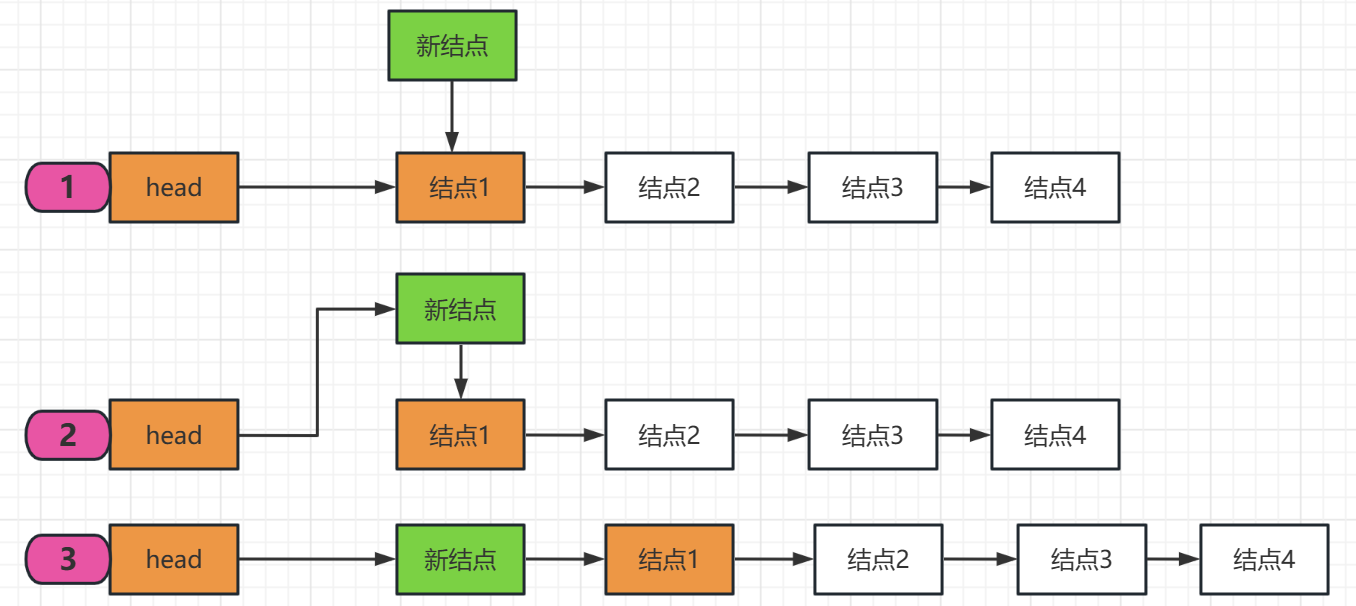
 出棧圖示：

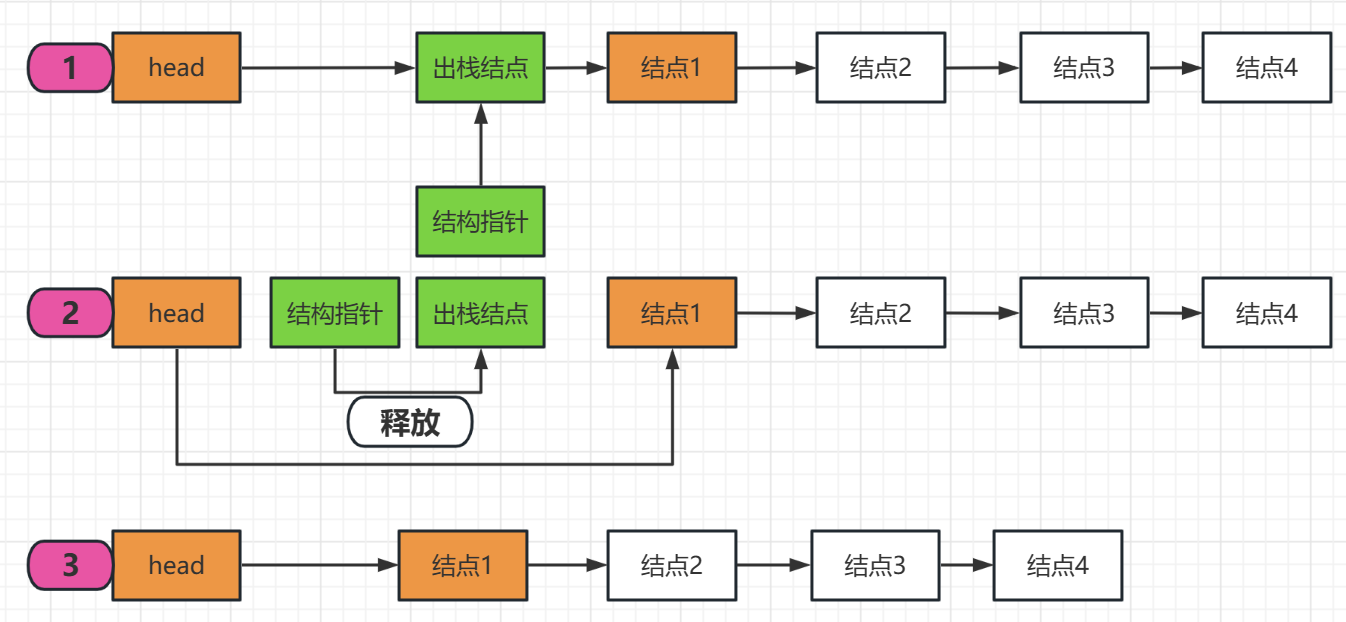
 三.棧的簡單應用

我們在簡述棧的時候就已經瞭解過了，對於中綴表示式轉字尾表示式的方法，當時我們使用的是加括號，然後通過我們人可理解的方式來解決的，

加括號可以快速的把中綴表示式轉換為前字尾表示式，但是這是我們人才能做到這麼快，但是機器呢？

對於計算機，他無法根據此規則加上相應的括號，然後移動符號，最後去掉括號，但是計算機它有一套自己的實現方法，也是通過棧來實現的

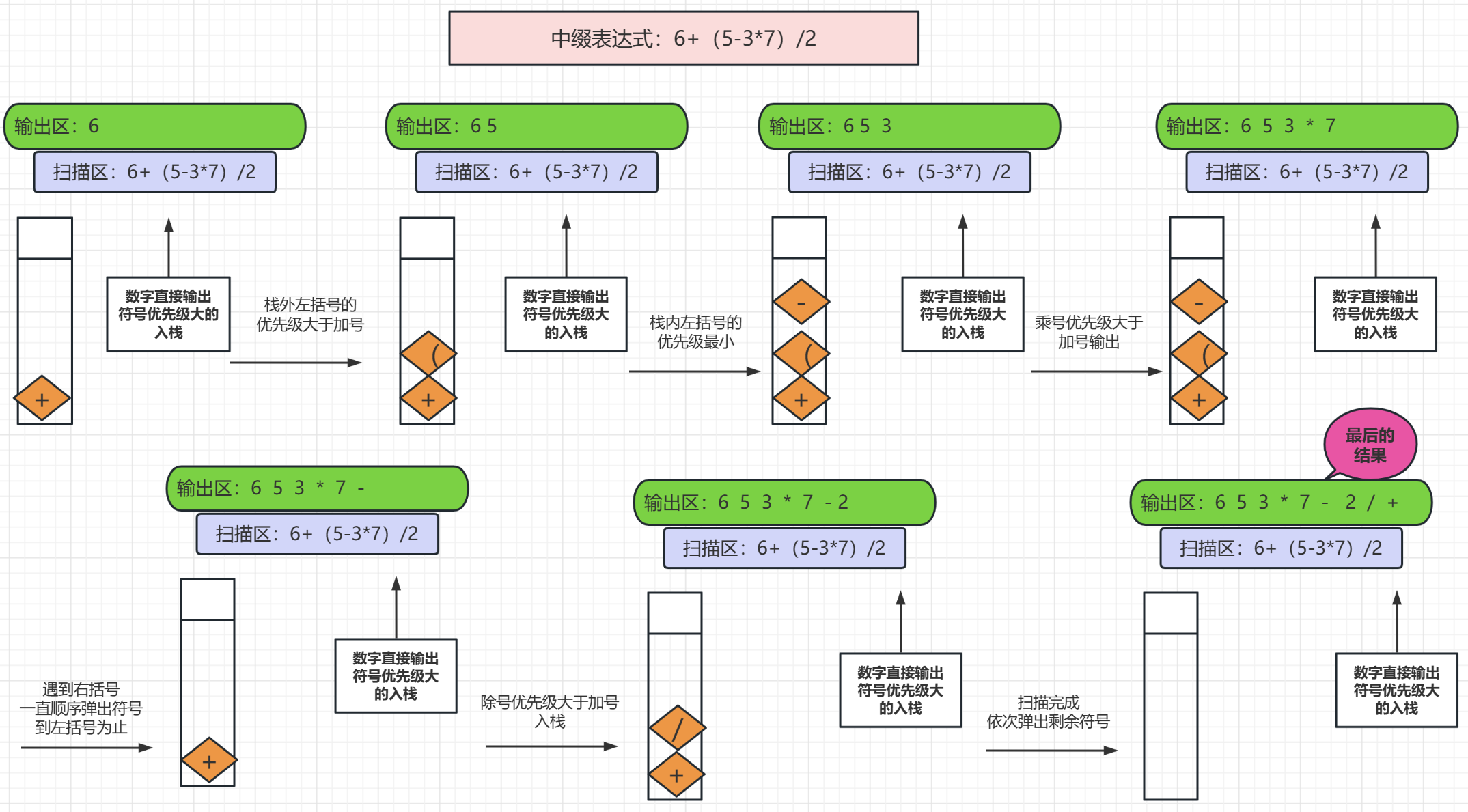
 通過上面的計算，利用棧的轉存就可以很輕鬆的計算出字尾表示式，當然他必須要滿足相應的一些規則：

中綴表示式從左向右掃描

• 遇到運算數位就直接輸出
• 左括號在棧外的時候優先順序最高，直接壓入棧中，在棧內優先順序最低
• 遇到右括號後，直接把左括號上的符號依次出棧，但是左右括號不需要再帶上了
• 其它運運算元，只要優先順序高的就入棧，比棧內的低的，棧內的彈出，然後與棧內繼續比較，同級的也是棧內的先彈出，然後棧外的入棧
• 物件掃描完以後，需要把棧內的殘餘的運運算元順序輸出

小結：

上面的操作並不是棧最常用的操作，棧作為最早出現的資料結構之一，其特點被大量的用在了底層中，作業系統中棧記憶體是不可或缺的一份子，它對斷點的記錄有著離奇好的效果，

廣泛用於作業系統的斷點記錄，函數回溯引數還原

包括整個遞迴思想都是在棧機制上建立起來的，如果沒有棧機制，遞迴的思想可能很難被實現出來

圖的深度優先探索，都需要棧來記錄它剛剛經過的地方，在道路不可達的時候，需要回到棧記錄原來的地方

回溯演演算法等等

-

-

-

-

-

-

 

部落格編輯於

---------------------浙江大學陳越老師《資料結構與演演算法》