【技術分享】萬字長文圖文並茂讀懂高效能無鎖 「B-Tree 改」：Bw-Tree

原文連結： https://mp.weixin.qq.com/s/I5TphQP__tHn6JoPcP--_w
參考文獻不一定能下載。如果你獲取不到這幾篇論文，可以關注公眾號 IT技術小密圈 回覆 bw-tree 獲取。

一. 背景

Bw-Tree 希望實現以下能力:

• 解決多核處理器效能瓶頸
  • 通過 CAS 操作實現 latch-free 能力, 提高多核 CPU 利用率。
  • 通過增量更新提高 CPU 快取命中率。
• 利用更為高效的快閃記憶體：雖然快閃記憶體有著相似的隨機讀速度和順序讀速度，但其隨機寫速度遠小於順序寫操作。 Log-Structured Store(LSS), 可以很好的利用這一點實現高效讀寫。

二. 基於 Bw-Tree 的儲存整體架構

對映表

快取層中維護著 對映表(mapping table), 儲存邏輯頁和物理頁的對映關係，邏輯頁由邏輯頁識別符號 PID 唯一標識。

對映表將 PID 對映為以下兩種地址之一:

• 快閃記憶體偏移量(flash offset): 持久化儲存中的頁的地址；
• 記憶體指標(memory pointer): 記憶體頁的地址。

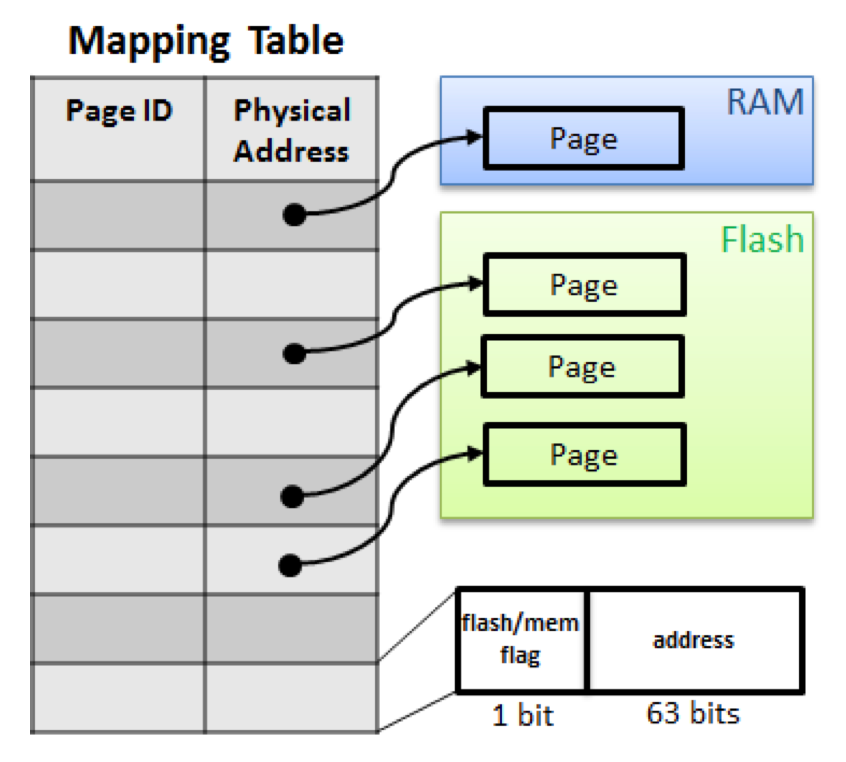
BW-Tree 的節點指標都是邏輯的 PID，因此在 SMO 操作過程中， 某些節點的實體地址發生變化，並不需要更新所有對該節點有參照的所有節點指標(PID 並沒有發生變化)。

增量更新

BW-Tree 通過建立描述變更內容的 增量記錄(delta record) 並將其插入到當前頁的前面來實現對頁的狀態變更。

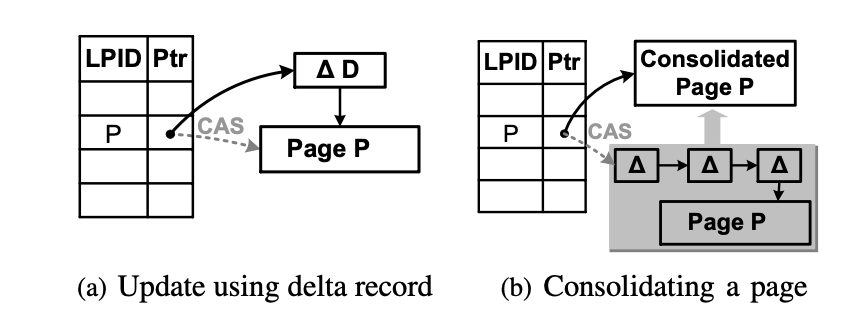
如下圖 (a) 中，先將對 Page P 的一次變更操作做成一個增量記錄 ∆D，並讓 ∆D 指向 Page P。然後將 Page P 的邏輯地址 PID P 對映的實體地址通過 CAS(compare and swap) 原子操作由 Page P 的實體地址改為 ∆D 的實體地址。(Page P 被稱為 Base 頁)

當變更導致前置的增量記錄達到一定的規模之後，會觸發合併操作，將所有的增量記錄和原本的頁合成一個新的頁。

如下圖(b) 中，將 Page P 前置的所有增量記錄和 Page P 一起合併為一個 Consolidated Page P， 然後通過 CAS 操作將 Page P 的邏輯地址 PID P 對映的實體地址替換為 Consolidated Page P 的實體地址。Page P 及其前置的所有增量記錄將會被垃圾回收機制回收處理。

紀錄檔儲存(Log Structure Store) 和 WAL(Write-Ahead Log) 紀錄檔

BW-Tree 在快閃記憶體中的儲存結構如下圖。當增量記錄(∆record)達到一定數量之後，會執行一次刷盤操作將所有 Base 頁的增量記錄一起順序寫入磁碟。

這將會導致每一個 Base 頁和它對應的許多 ∆record 並不在相鄰的地址內，而快閃記憶體的隨機讀效能和順序讀效能幾乎一致，因此可以接受。(如果是其他順序讀效能更好的持久化儲存可能需要一定優化，後文有提及。)

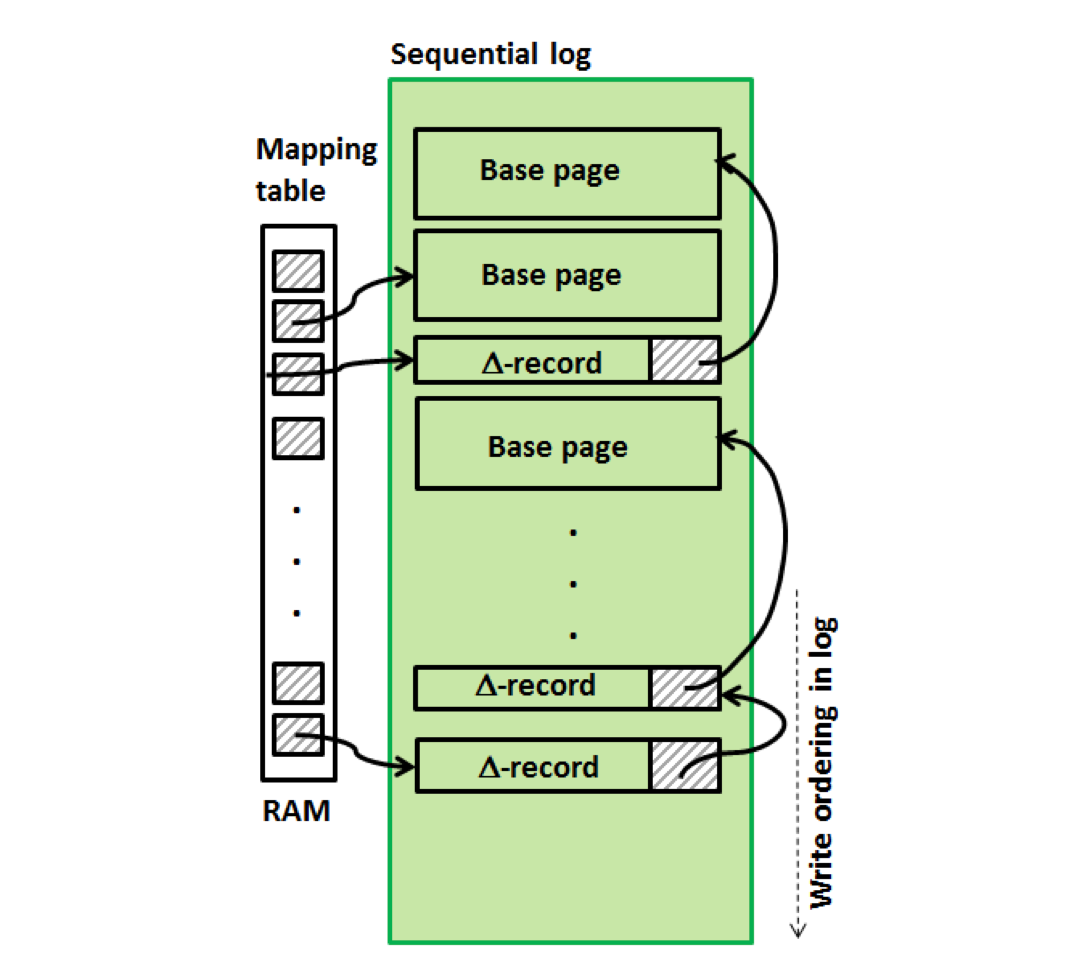
如上文所述， 並不是所有的變更操作都立即刷盤(而是會等待增量記錄達到一定數量規模才會一次刷盤)。因此，在每次執行變更前，記錄 WAL 紀錄檔也是必要的。

給每一次變更操作一個紀錄檔序列號(LSN), 當某次刷盤完成之後， 對應的最新 LSN 之前的 WAL 紀錄檔都可以失效。

BW-Tree 架構

整體架構

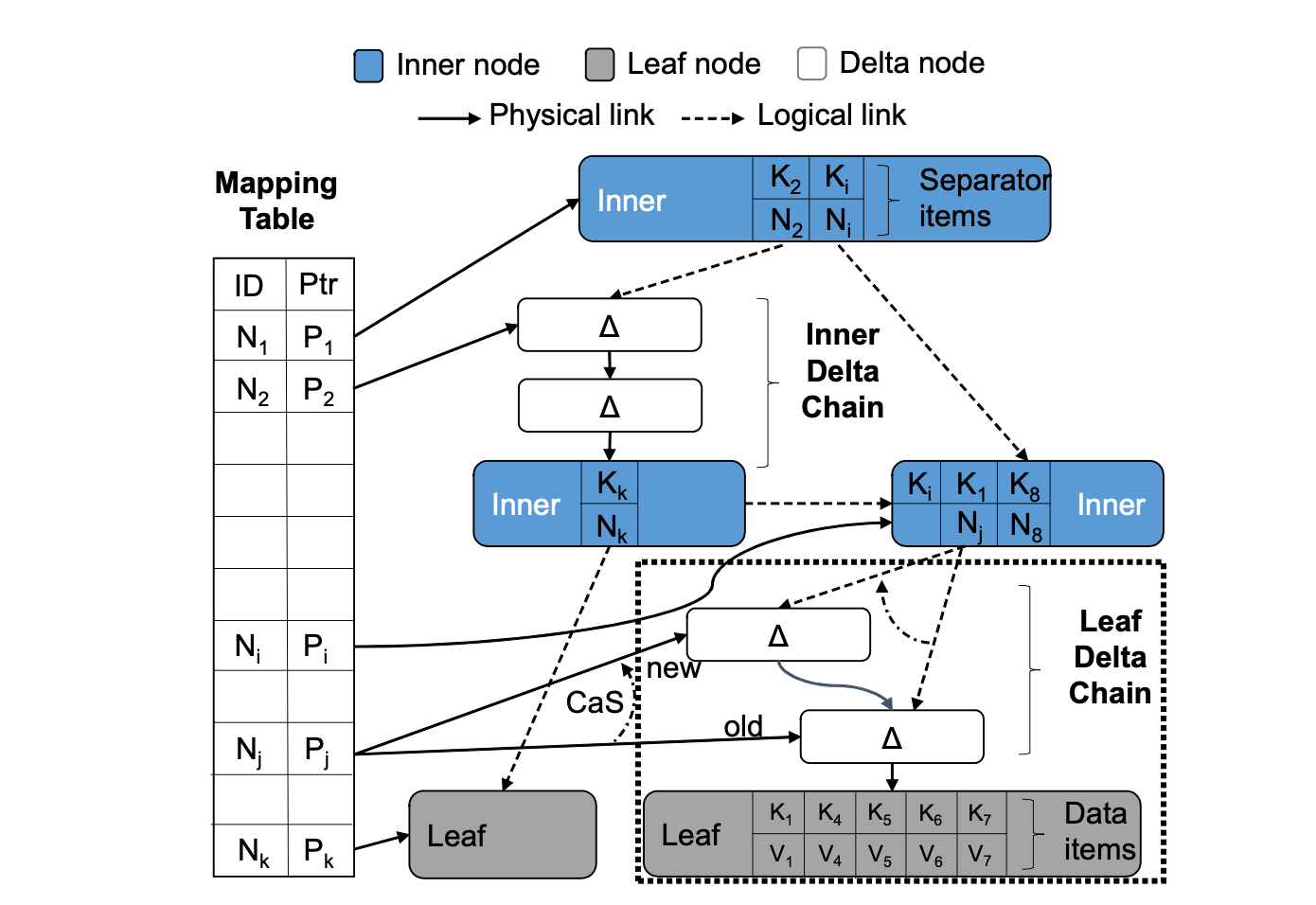
如上圖所示， BW-Tree 的每個節點都有唯一的邏輯地址 PID(N1, N2, ..., Ni, ..., Nj, ..., Nk, ...) 。節點之間不使用實體地址，而是使用邏輯地址 PID 相互參照。

當需要獲取某個節點的實體地址時，會先查詢對映表，將 PID 轉化為實體地址。 因此在對單個原子的 CAS 指令就能實現對有多個參照的節點的實體地址進行變更。

BW-Tree 和其他基於 B+tree 索引直接最大的不同在於 BW-Tree 避免直接操作樹的節點，而是直接將節點的增刪改查儲存增量記錄中，這樣極大地減少了 CPU 快取失效的概率。

另外將每個 Base Page 的變更維護在一條 增量鏈(Delta Chain) 中，並通過中間層對映表隔離 Page 地址的變更(PID 保持不變), 使得可以在一次原子 CAS 中實現對 Page 進行變更操作。

邏輯節點的實現細節(Base 節點和 Delta 鏈)

如下圖所示，在 BW-Tree 中，一個邏輯節點包含兩部分: Base 節點和 Delta 鏈。Base 節點記錄當前節點的在上一次合併(consolidate) 之後的資料，Delta 鏈記錄在此之後 Base 節點發生的所有變更操作。

Delta 鏈將對 Base 節點的操作按照時間順序用單向連結串列(物理指標)連線起來，連結串列的結尾處指向 Base 節點。

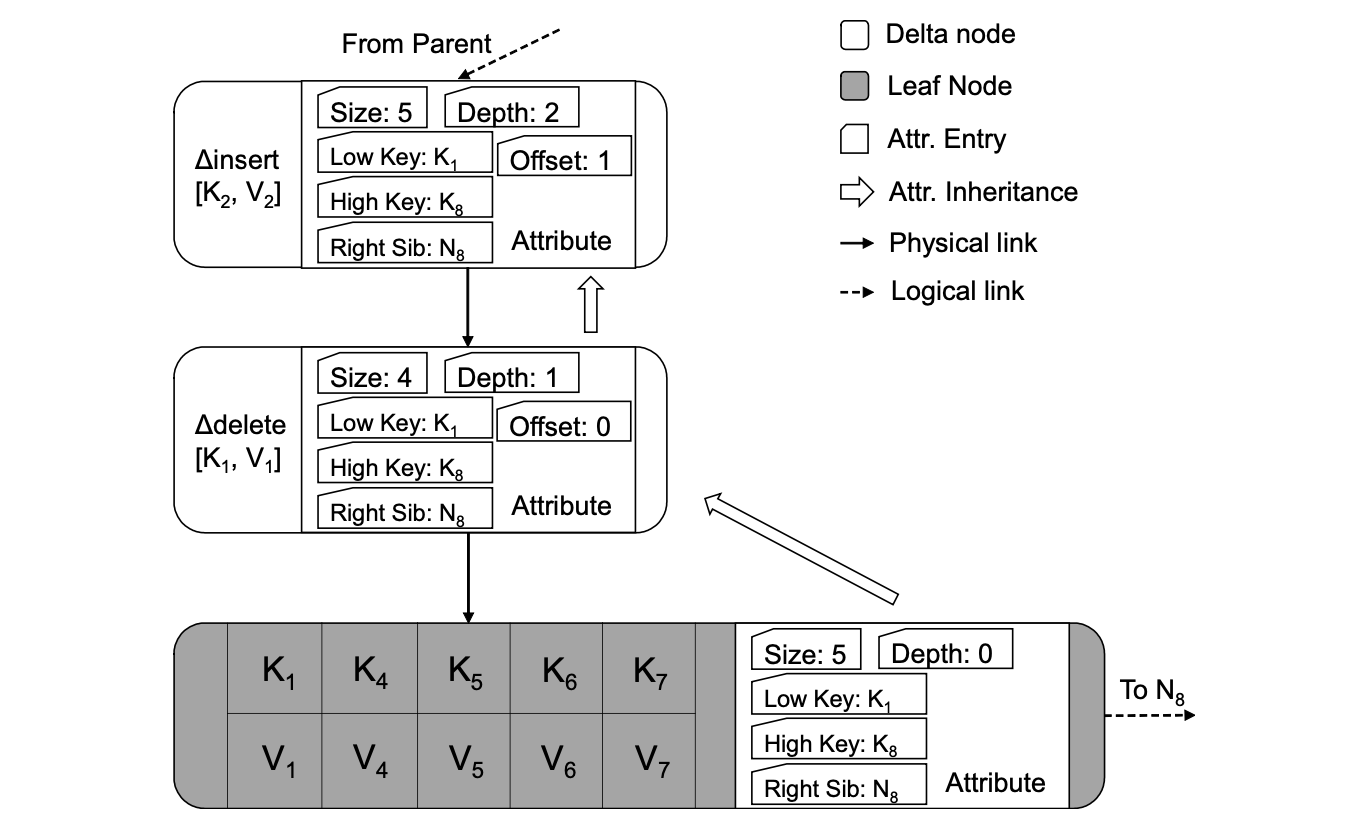
Base 節點和 Delta 鏈中的每一條 Delta 記錄都儲存了一些額外的後設資料資訊，它標識邏輯節點在某次操作時的狀態(每次對某個節點做變更操作，都會將最新的狀態記錄在最新的 delta 記錄中)。這些資訊將會用於樹的遍歷等操作。

下表解釋了這些後設資料的內容。

• low-key, high-key ：當前邏輯節點的資料範圍在區間 [low-key, high-key)。如上圖中，邏輯節點的資料範圍始終未變，在每個 Delta 記錄及 Base 節點中都是 [K1, K8)。
• right-sibling: 指向右兄弟節點的邏輯地址(類似於 B-link tree)。如上圖的兄弟節點 PID 為 N8。
• size: 記錄當前邏輯節點的大小。如上圖中。Base 節點的 size 為 5；在執行完 ∆delete [K1, V1] 操作後，size 變為了 4；在執行完 ∆insert [K2, V2] 操作後，size 又變為了 5。
• depth: 記錄當前 Delta 記錄在 Delta 鏈中與 Base 節點的距離。如上圖中， ∆delete [K1, V1] 操作的 depth 為 1, ∆insert [K2, V2] 操作的 depth 為 2。
• offset：待操作的資料在當前 Base 節點的位置(而不是邏輯節點的位置，也就是說，不關 delta 鏈中其他節點什麼事兒)。如上圖中，∆delete [K1, V1] 操作中，K1 在 Base 節點的第一位，因此它的 offset 為 0。∆insert [K2, V2] 操作中，K2 在 Base 節點的第二位，因此它的 offset 為 1。

BW-Tree 的結構操作(Structure Modification Operation, SMO)

BW-Tree 的所有 SMO 操作都是通過原子操作實現的 latch-free 操作, 它將單個的 SMO 操作拆分為一些列 CAS 原子操作。為了確保沒有執行緒需要等待其他執行緒的 SMO 操作結束，當它發現部分完成的 SMO 操作時，會在執行當前執行緒原本的任務之前，先將部分完成的 SMO 操作剩下部分執行完成。(help-along protocol)

下面本文將會詳細介紹 BW-Tree 具體是如何實現這樣的能力的。

分裂(Split)

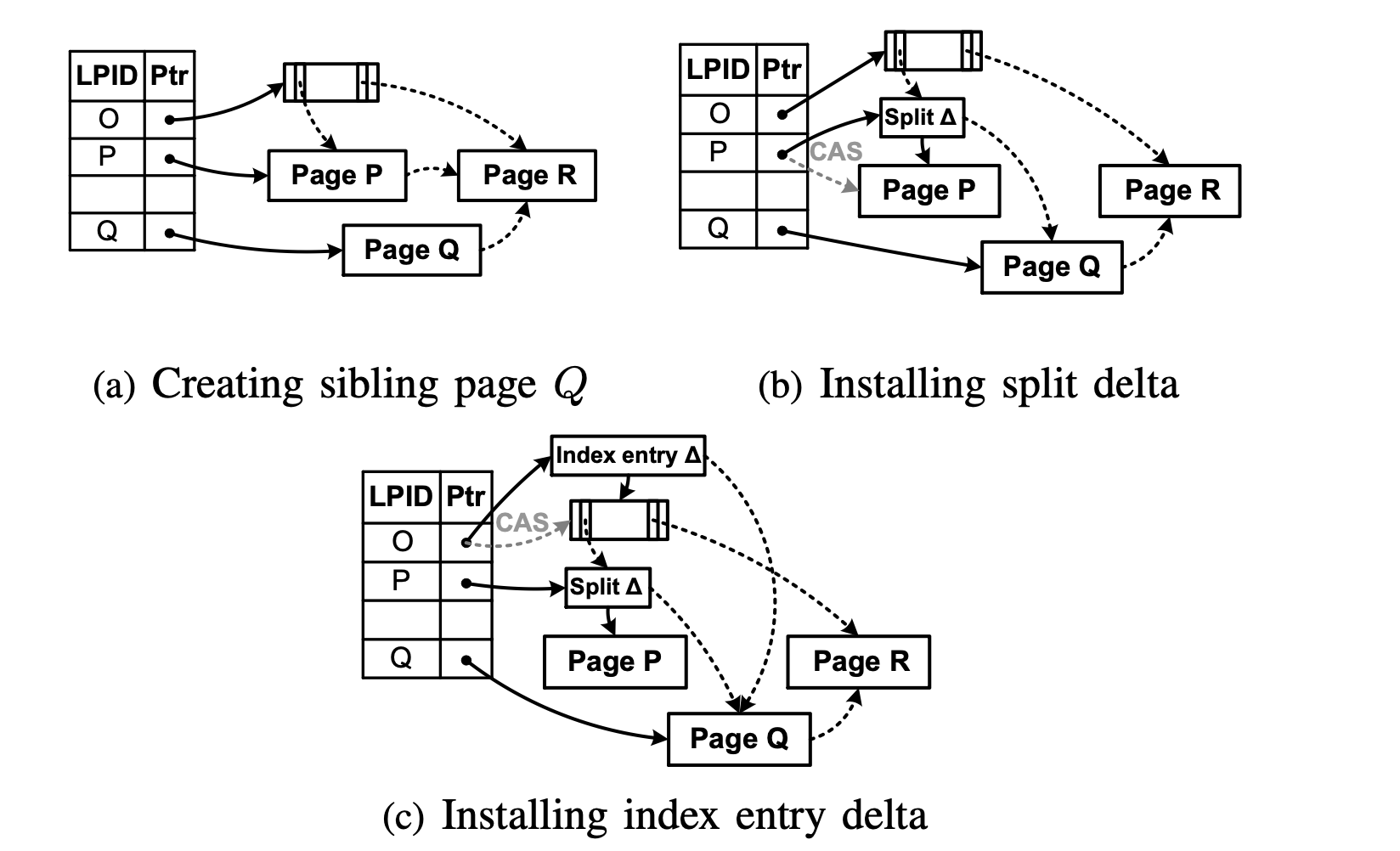
與 B-link tree 類似， BW-Tree 將 split 分為兩個階段: 先將子節點用原子操作拆分為兩個節點(half split), 然後將新的 分隔鍵(separator key) 和剛拆分的子節點的指標用原子操作更新到其父節點。

以上圖將 O 節點的子節點 P 拆分為 P 節點和 Q 節點為例:

1. 拆分子節點(half-split)
   (a) 建立 P 節點的兄弟節點 Q: 如上圖 (a) 所示。申請一個新的 Page 作為 Q 節點；在節點 P 中找一個合適的鍵 Kp 作為節點 P，Q 的分隔鍵(separator key)。

   節點 P 僅保留小於 Kp 的資料，大於等於 Kp 的資料將拷貝到節點 Q；將節點 Q 的兄弟節點設為節點 R(即當前節點 P 的兄弟節點)；將節點 Q 註冊到地址對映表中。

   整個流程中，節點 Q 均不被使用者可見，因此不需要原子操作。在這個階段節點 P 依然處於為分裂狀態。

   (b) 更新 P 節點, 將 Q 節點作為其兄弟節點：如上圖 (b) 所示。為節點 P 建立執行分裂操作的 delta 記錄(Split ∆), 該記錄包含兩個資訊: 將 Kp 作為節點 P，Q 的分隔鍵以及讓 Q 節點作為 P 節點的兄弟節點(讓 P 邏輯節點的兄弟節點指標 right-sibling 指向 Q 節點的邏輯地址 Q)； 然後呼叫 CAS 原子操作將邏輯地址 P 指向 Split ∆ 的地址。

   當 CAS 操作完成時，對節點 P, Q 的所有查詢，都將會被父節點 O 路由到 P 邏輯節點(Split ∆)。如果待查詢的 K 小於 Kp, 查詢將會被路由到節點 P。若 K 大於等於 Kp, 查詢將會通過 right-sibling 路由到節點 Q。

2. 更新父節點：要實現直接從父節點 O 路由到剛被分裂的節點 Q(而不經過節點 P)，需要將節點 Q 的資訊更新到節點 O 中。如上圖 (c) 所示。 先建立一個指向節點 O 的 Delta 記錄 Index entry ∆，它包含了三個資訊: (a) 節點 P， Q 的分隔鍵 Kp； (b) 指向節點 Q 的邏輯地址；(c) 節點 Q 和其 right-sibling 的分隔鍵 Kq(Kp 和 Kq 確定出節點 Q Key 的範圍 [Kp, Kq))。

合併(Merge)

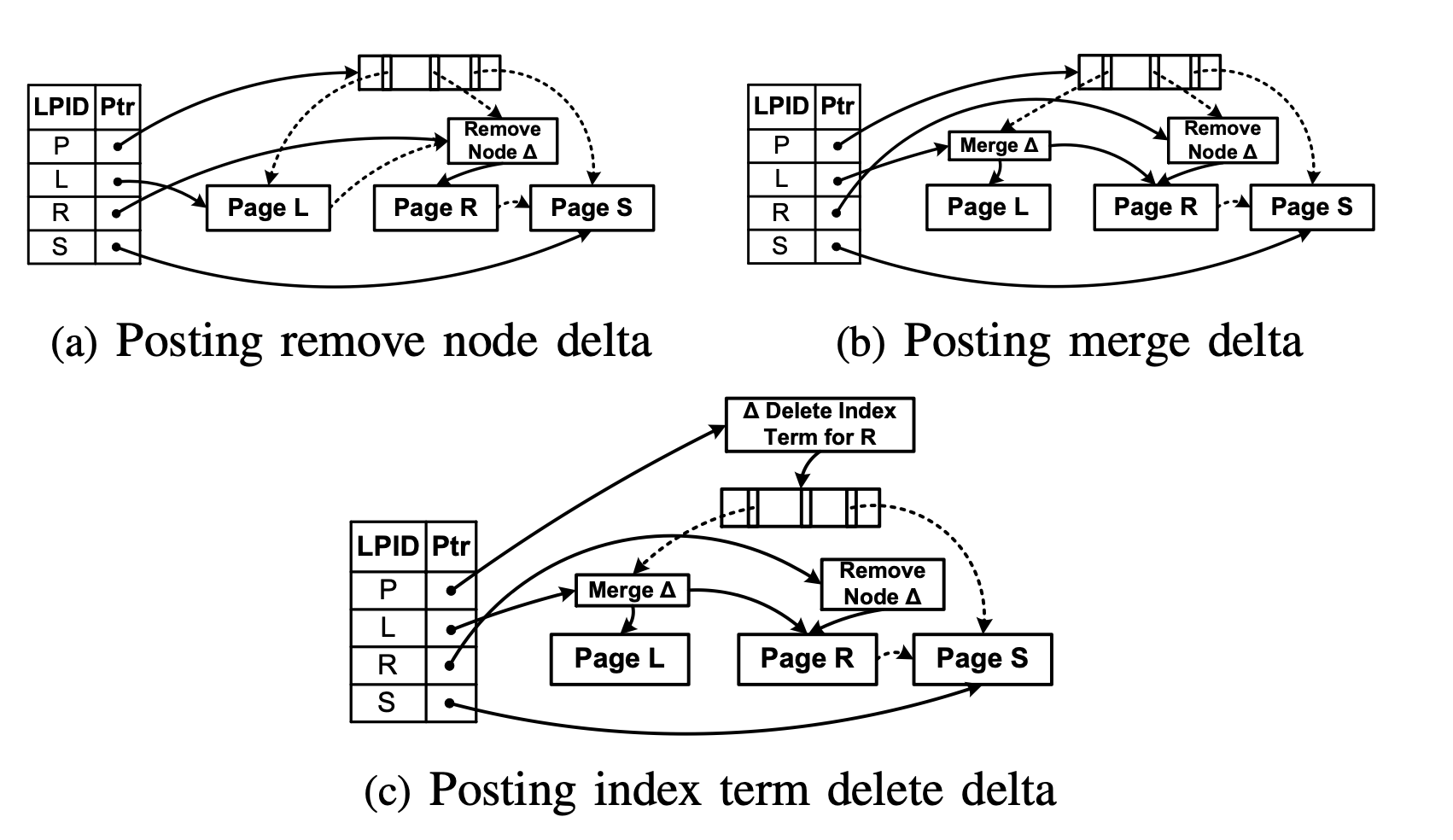
如上圖所示，當某個節點的大小小於某個閾值，BW-Tree 將使用 latch-free 的方式將它合併到其他節點(BW-Tree 僅支援與左兄弟節點合併)。

以上圖將 P 節點的子節點 R 合併到節點 L 為例：

1. 將 R 節點標記為刪除: 如上圖 (a) 所示。為節點 R 新增 Delta 記錄 Remove Node ∆, 用於將邏輯節點標記為刪除。當查詢存取到 Remove Node ∆ 節點，將會跳轉到節點 R 左邊的兄弟節點，即節點 L。

2. 合併子節點： 如上圖 (b) 所示。為節點 L 新增 Delta 記錄 Merge ∆，該記錄將節點 L 與節點 R 合併起來作為一個邏輯節點整體。

   在步驟 1 到步驟 2 之間，實際上是無法感知到節點 R 的。(因為節點 R 已經被Remove Node ∆ 節點邏輯移除了 )。在步驟 2 執行之後， 才能通過 Remove Node ∆ 跳轉到 R 的左兄弟節點 L， 通過 Merge ∆ 查詢到節點 R 的值。

   但是這並不會影響並行操作的正確性，因為 help-along protocol 會保證在發現其他執行緒存在未完成 SMO 操作的情況下，先將 SMO 操作執行完成，再進行原本的操作。因此就不會在步驟 1 到步驟 2 之間去對節點 R 進行操作。

3. 更新父節點: 如上圖 (a) 所示。父節點新增 Delta 記錄 ∆ Delete Index Term for R，用於將節點 R 在父節點中的索引刪除。節點 L 將節點 R 的索引範圍也納入其中。

   在這個階段之後，Remove Node ∆ 這個 delta record 和節點 R 在地址對映表中的位置都將不再被使用， 他們將會被 epoch GC 邏輯回收。

點查詢(Search)

• 唯一鍵查詢: 唯一建的查詢和普通的 B+ 樹類似，唯一的區別在於，當遍歷到葉節點時，如果存在 Delta 鏈，它會先依次遍歷 Delta 鏈，並將最先出現的結果返回。當 Delta 鏈中不存在時，才會去 Base 節點執行二分查詢。

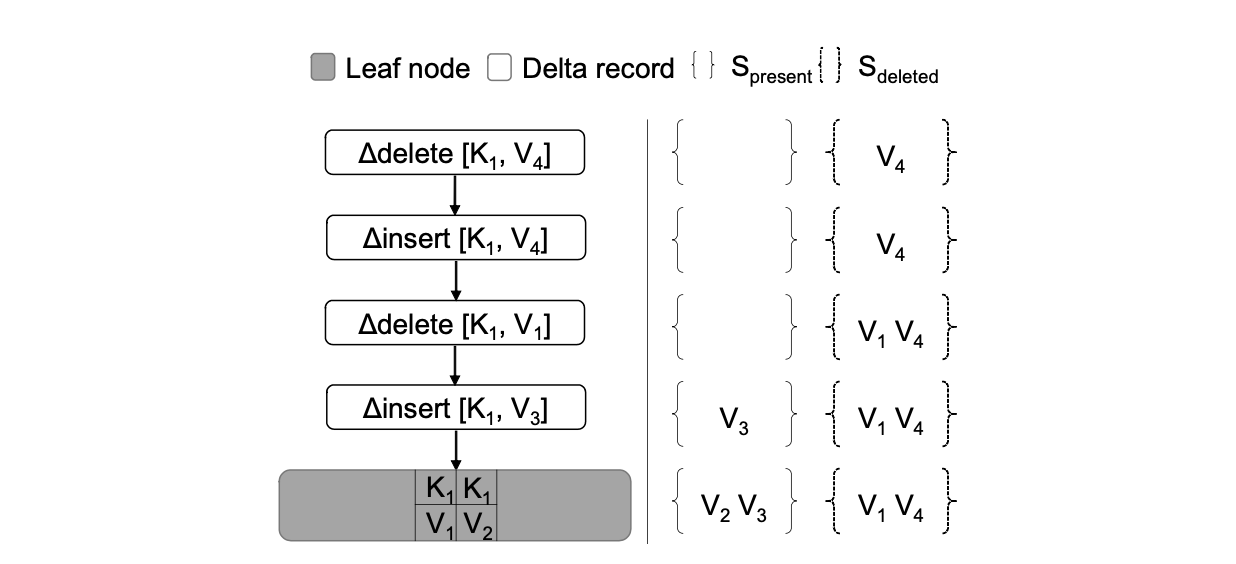
• 非唯一建查詢：當定位到資料僅可能存在在某個葉子節點時，必須遍歷所有的 Delta 鏈和 Base 節點才能查詢出指定鍵的所有值。操作邏輯如下圖。

  在遍歷 Delta 鏈的過程中，將已知符合要求的資料放在集合 Spresent, 將已知被刪除的資料放在集合 Sdeleted。按順序遍歷 Delta 鏈時，當遍歷到插入 Delta 記錄(K, V) 時，如果 V 不在 Sdeleted，則將其加入 Spresent。當遍歷到刪除 Delta 記錄(K, V) 時，如果 V 不在 Spresent，則將其加入 Sdeleted。

  記 Sbase 為 Base 節點中的該鍵的所有值的集合。 則最終的查詢結果為 Spresent ∪ (Sbase - Sdeleted)

遍歷(Scan)

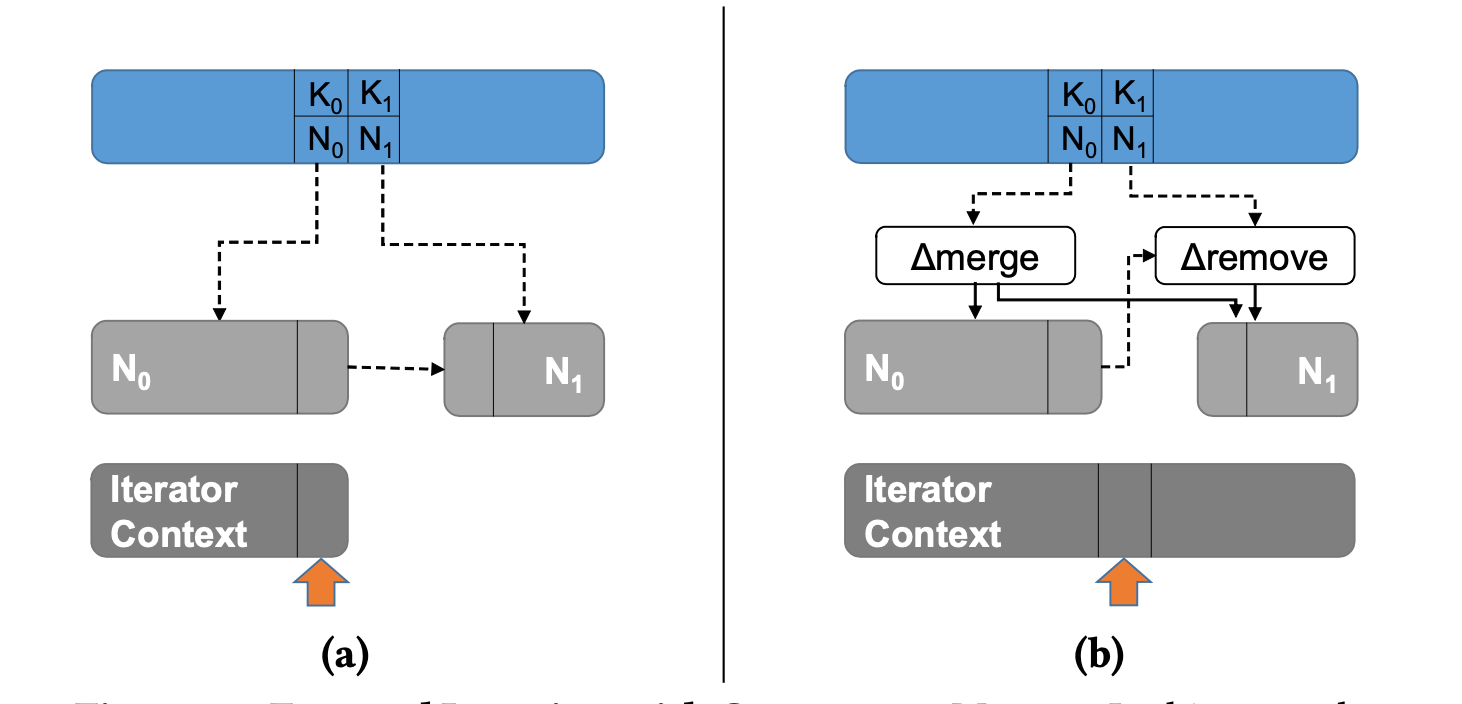
• 正向 Scan: 正向遍歷會將正在處理的節點拷貝到迭代器中。當迭代器中儲存的節點的資料全部遍歷完成，就會繼續將下一個節點的資料全部拷貝到迭代器繼續遍歷。因此，整個 Scan 過程讀取的資料並不是一個快照(snapshot)的資料。

  如下圖所示，當遍歷完一個節點 N0 [K0, K1) 的資料，會查詢該節點的上界 K1 所在的節點作為下一個節點。 如果遍歷 N0 過程中, N0 發生的 SMO 操作是的 N0 鍵的範圍變大, 該節點的上界 K1 所在的節點依然是 N0, 則將新的 N0 拷貝到迭代器中。然後查詢到 K1 的位置，繼續遍歷該節點。

• 反向 Scan：反向 Scan 整體邏輯和正向 Scan 一致。唯一的區別在於反向 Scan 的下一個節點的查詢方式有所不同。反向 Scan 遍歷完一個葉子節點後，會將小於該葉子節點的下界的最大的 Key所在的葉子節點作為下一個遍歷的節點。

  如下圖，N1 的下界是 K5， 小於 K5 的最大鍵為 K4(N0)， 因此, K4 所在的節點 N0 就是就是 N1 遍歷完之後，下一個需要遍歷的節點。

對 BW-Tree 的優化

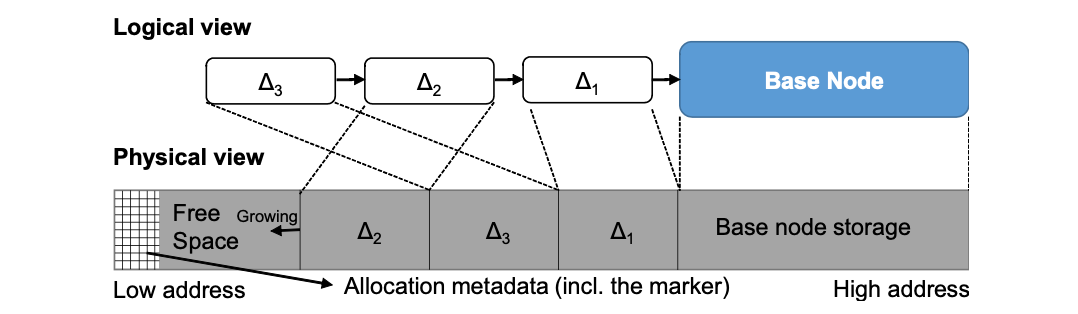
• Delta 記錄的預分配: 如下圖， 提前為記憶體中的 Delta記錄預分配記憶體空間，減少記憶體碎片。

• 用去中心化 Epoch GC 替代中心化 Epoch GC

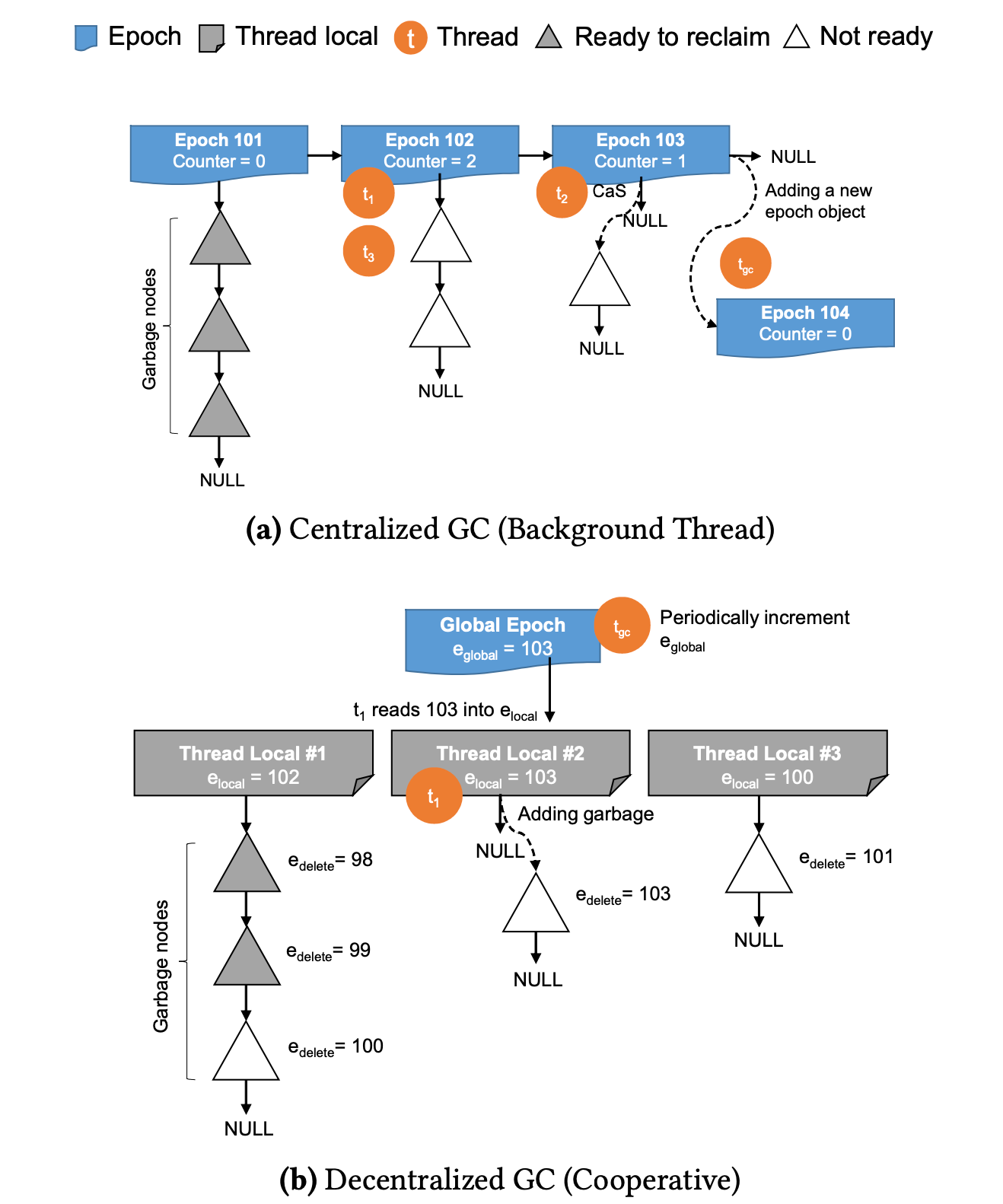
  • 中心化 Epoch GC： 如下圖 (a) 所示， 唯一的 GC 執行緒(Background Thread) 維護 Epoch 連結串列。每個 Epoch 節點維護參照當前 Epoch 刪除的資源及其參照執行緒數的總和。當某個 Epoch 的執行緒參照計數恢復 0 時，該 Epoch 及其維護的垃圾資源可以被刪除。如下圖中的 Epoch 101。

  • 去中心化 Epoch GC：
    (1) 全域性 Global Epoch 維護全域性 Epoch 時鐘 e_global。每個工作執行緒產生的垃圾節點由本執行緒維護在本地垃圾回收連結串列 l_local, 並將該垃圾節點的 e_delete 設定為當前程序的 e_local。

    (2) 當某個執行緒開始索引操作時，會先將當前的全域性 Epoch 時鐘 e_global 拷貝到當前執行緒，記作 e_local。當該索引操作結束後，會再次將 e_local 重新整理為 e_global。
    (3) 每個工作現場會定期獲取當前全域性最小的 e_local, 並將本執行緒維護的 l_local 中 e_delete 小於全域性最小 e_local 的垃圾節點回收。

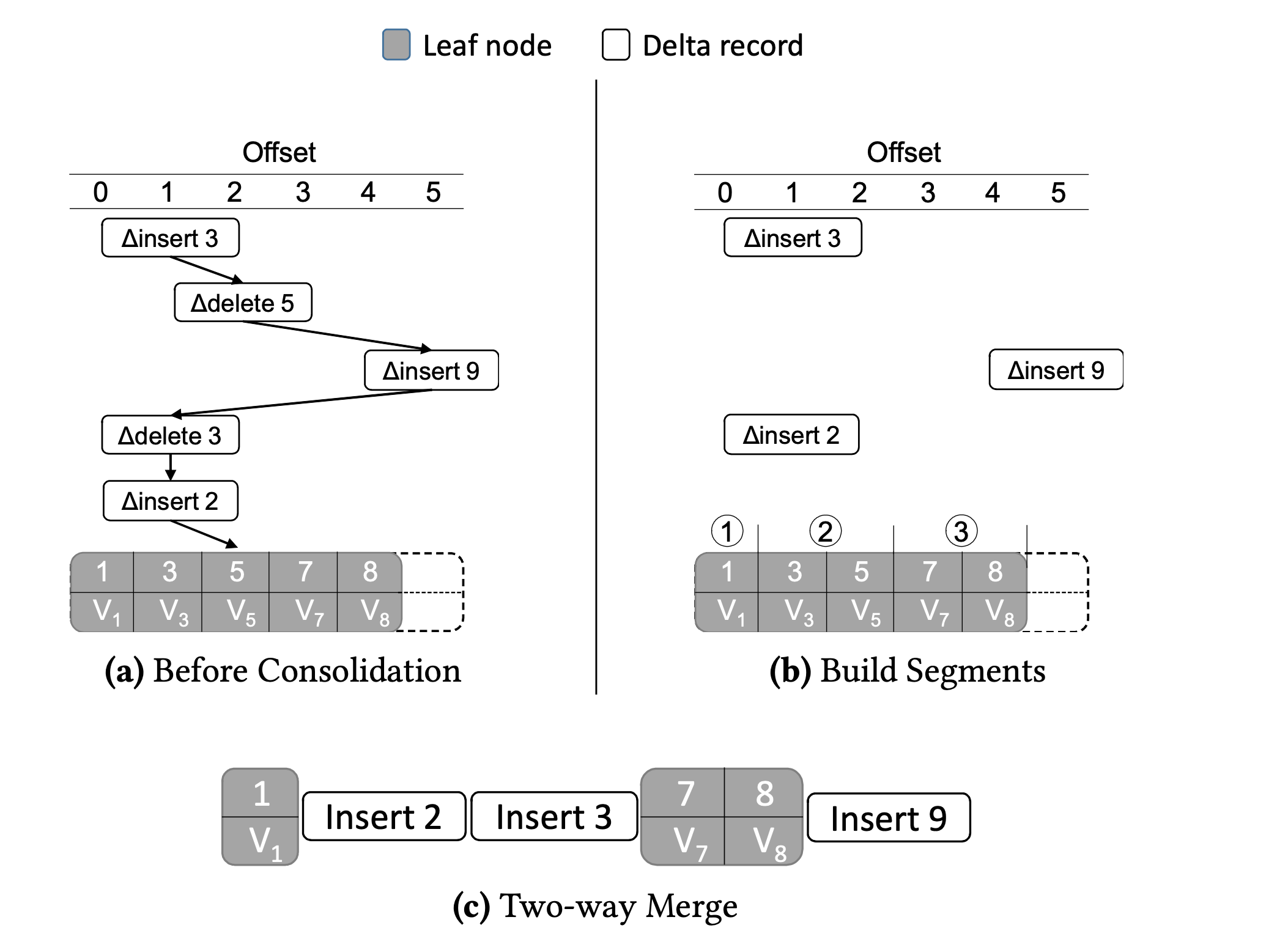
• 快速整合(Fast Consolidation):
  • 將原 Base 節點的鍵區間作為一個整體 [start, end). 依次遍歷 Delta 鏈，將鍵區間分為多個部分。
    (1) 當遍歷到插入 Delta 記錄，則將當前記錄所在區間 [s, e) 拆分為 [s, offset) 和 [offset, e)。
    (2) 當遍歷到刪除 Delta 記錄，則將當前記錄所在區間 [s, e) 拆分為 [s, offset) 和 [offset+1, e)。
    (3) 如果刪除 Delta 記錄刪除的資料不在 Base 節點中，則忽略該記錄。
  • 上述操作將 Base 節點拆分為多個部分。然後將拆分的多個部分和新插入資料一起整合成新的 Base 節點。

• 節點搜尋快捷方式(Node Search Shortcuts)

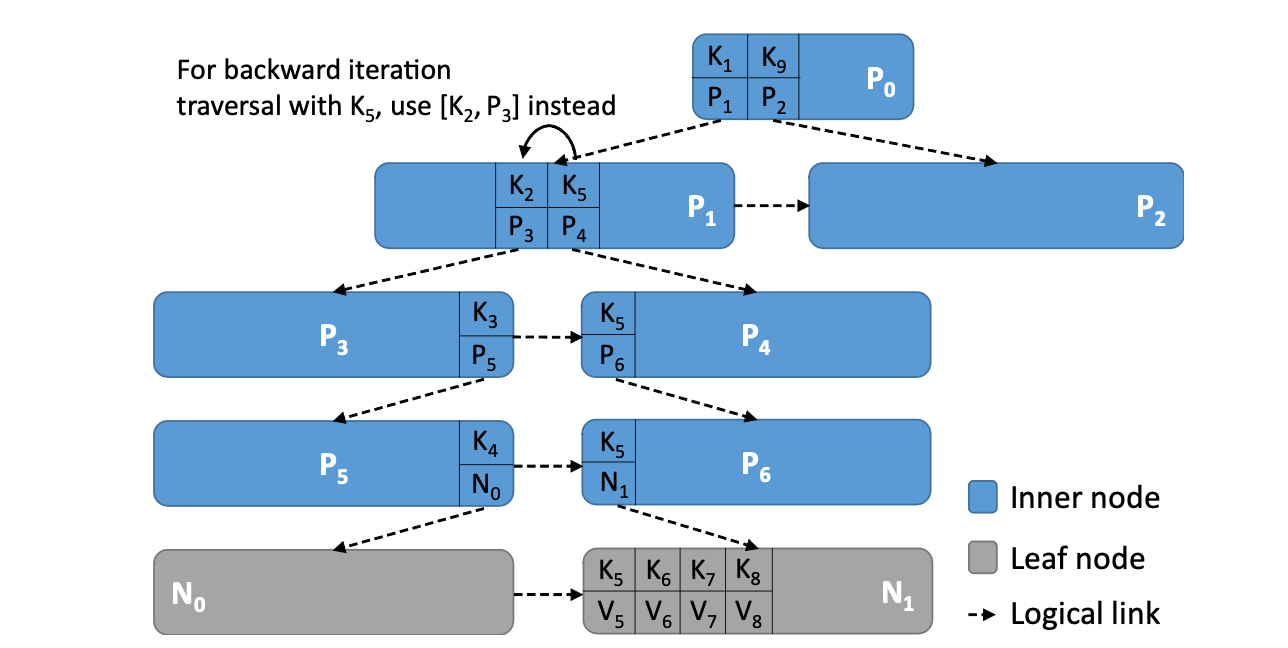
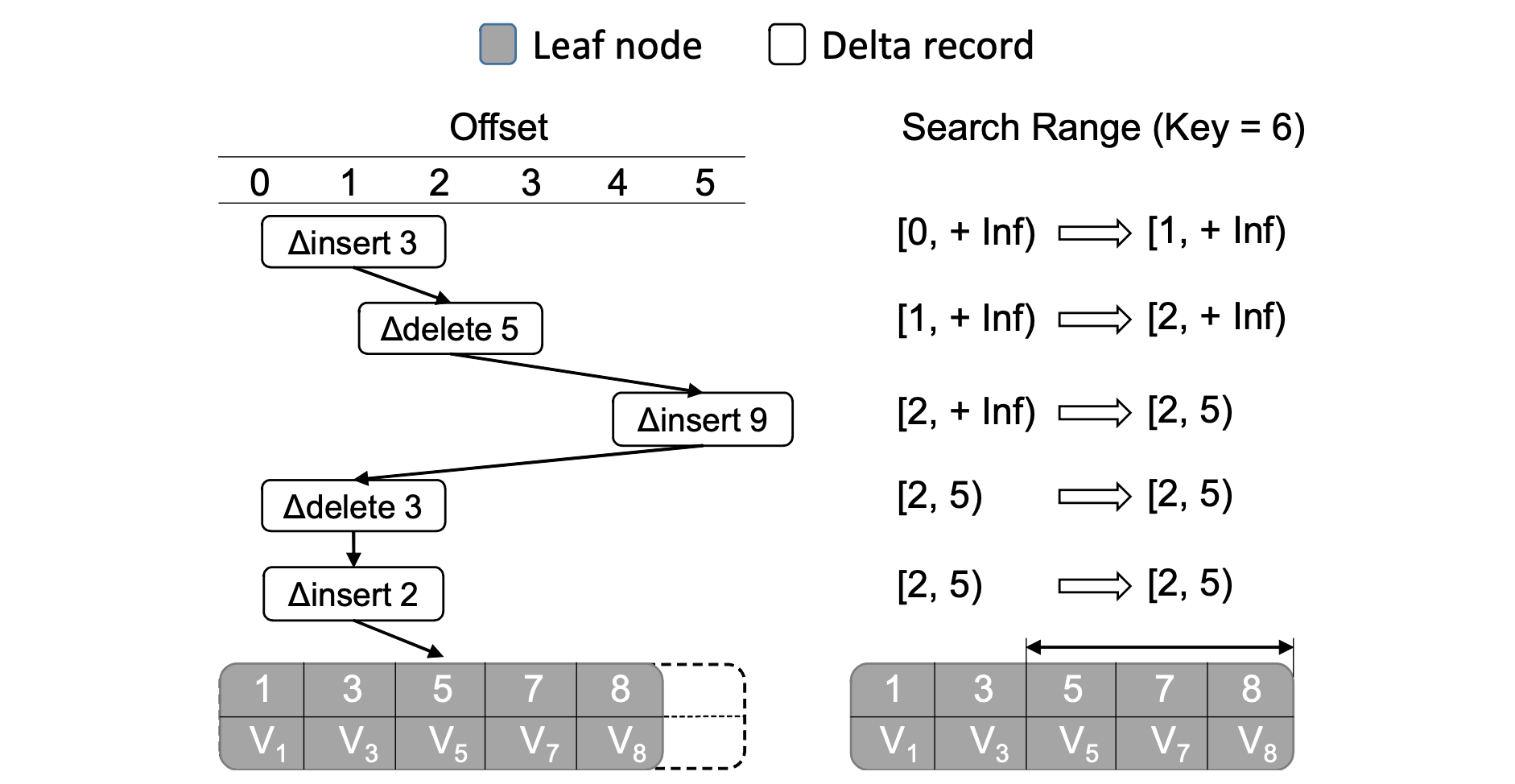
  • 當工作執行緒遍歷 Delta 鏈查詢鍵 K 時， 它會初始化二分查詢的偏移量(offset) [min. max) 範圍為 [0, +inf)。遍歷過程中，當遇到鍵位 K', 偏移量為 offset 的 ∆insert 或 ∆delete 記錄，它會比較 K 與 K'。若 K=K', 則立即得到 K 所在偏移量為 `[offset, offset+1)``，不用在 Base 節點進行二分查詢。若 offset > min 並且 K>K′， 則將 min 設為 offset。 若 offset < max 並且 K <K′， 將 max 設為 offset。如果最後的區間大小大於 1， 則在偏移量區間內二分查詢鍵 K。

  • 如下圖中的例子， 最終得到的區間是 [2, 5), 因此最後只需要在 Base 節點中 offset 在 [2. 5) 區間內的鍵二分查詢 Key=6。

其他

本文更多的是介紹記憶體內的 BW-Tree 的維護邏輯，更多關於持久化資料的維護相關的內容請檢視 LLAMA: A Cache/Storage Subsystem for Modern Hardware。後續我也會在公眾號 IT技術小密圈 更新對該論文的分享，歡迎關注。

參考文獻

• Building a Bw-Tree Takes More Than Just Buzz Words
• The Bw-Tree: A B-tree for New Hardware
  Platforms
• LLAMA: A Cache/Storage Subsystem for Modern Hardware

參考文獻可能不太好下載。如果你獲取不到這幾篇論文，可以關注公眾號 IT技術小密圈 回覆 bw-tree 獲取。