減法器的設計與實現並用譯碼器顯示16、10進位制
大家新年好,我是呼嚕嚕,在上一篇簡易加法器裡我們瞭解了半加器和全加器的設計與實現,今天我們來看下CPU中減法器是如何實現的。文章比較長,大家可以收藏反覆觀看
計算機為什麼利用反碼來實現減法?
我們來看一個最常見的例子,2-1 =1這是減法,但它等同於 2+ (-1) =1 這其實是加法。從運算邏輯上來說,減法可以通過加法來實現,這是可行的。
從硬體電路層面說,我們很容易讓電子實現彙總的效果,但是將電子群拆分出多個更小的叢集,是不容易的。還有一個好處是利用加法器能實現減法的效果的話,就不需要再為減法器專門設計電路了,降低了電路的複雜度。
由於計算機採用的是二進位制,和我們天生熟悉的十進位制還是有區別的,那麼二進位制能否實現用加法來實現減法效果?
很幸運地是,當初那群計算機那群工程師大拿將二進位制玩的是爐火純青,通過原碼->反碼->二補數,一步步實現了二進位制通過加法來實現減法效果。其中原理大家感興趣地,可以看看筆者之前的一篇文章 計算機中數值和字串怎麼用二進位制表示?
二補數真的是一個天生完美的奇妙存在,基於二補數的機制,減法可以轉化為加法,也就意味著計算機可以通過加法器實現減法。
看完筆者的那篇文章,我們知道了二補數產生的手動:正數原碼不變,負數的符號位不變, 其餘各位取反, 最後一位+1
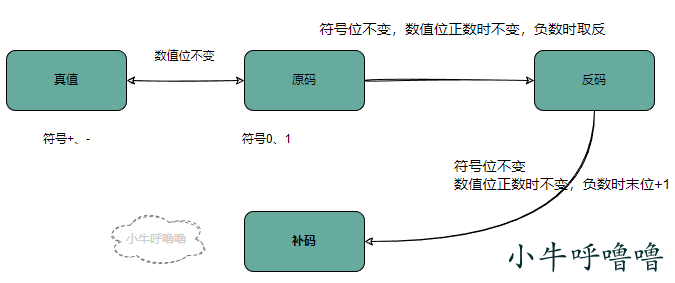
減法器的實現
要實現原碼到二補數的轉換,需要一個取反器,我們先來寫出減法邏輯的真值表:

通過真值表,我們可以很容易發現這其實就是一個互斥或門(相同為0,不同為1)
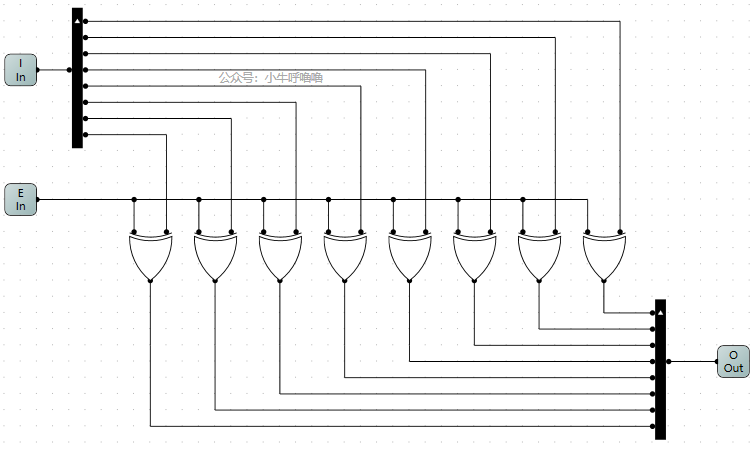
我們來實現一個8位元的取反器,由於是8位元的,所以輸入選這8位元輸入,還得連一個8位元的分線器,輸出類似。互斥或門得有8個,每個都需和控制是否取反的輸入相連。
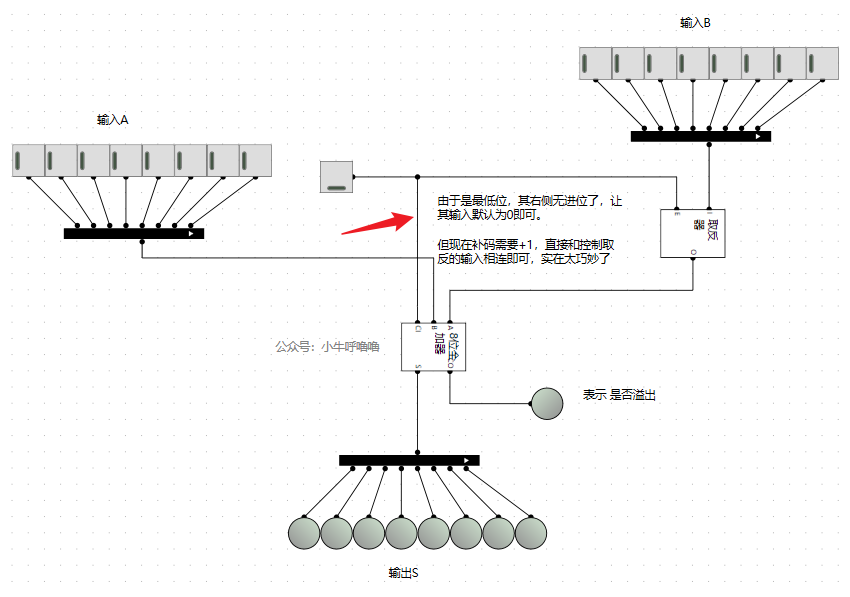
我們將之前的全加器和減法器結合起來,需要注意的是二補數需要取反再+1,取反可以將輸入和取反器相連,+1可以將全加器最低位的進位與控制取反的輸入相連即可,極簡單又巧妙
我們來啟動模擬,看下效果:
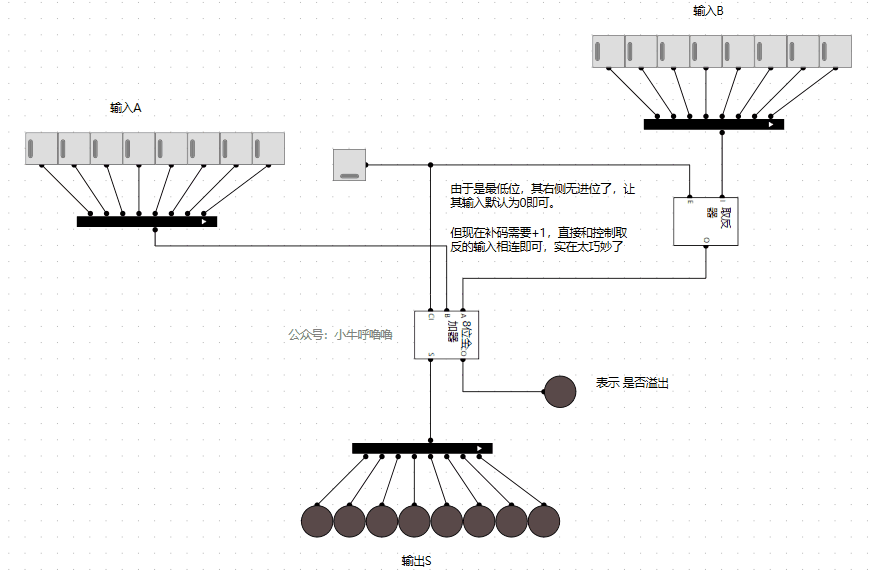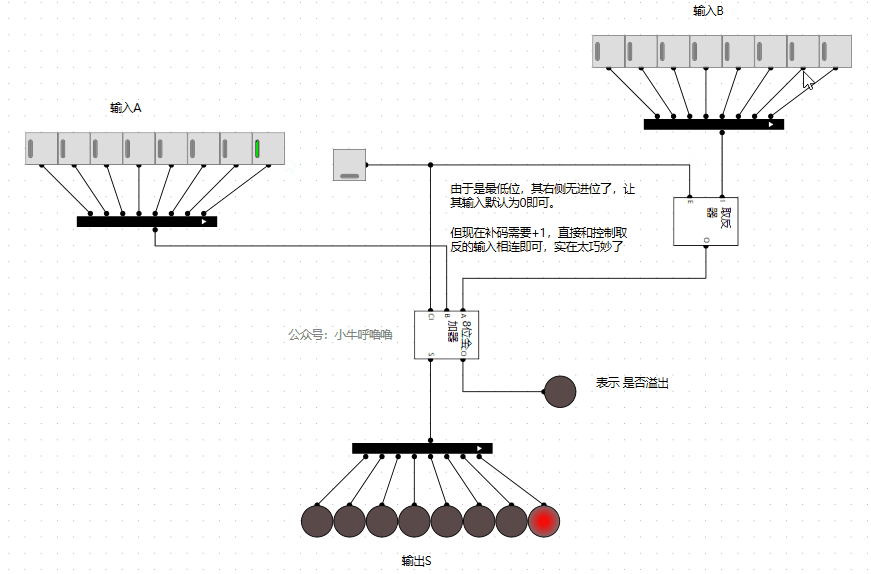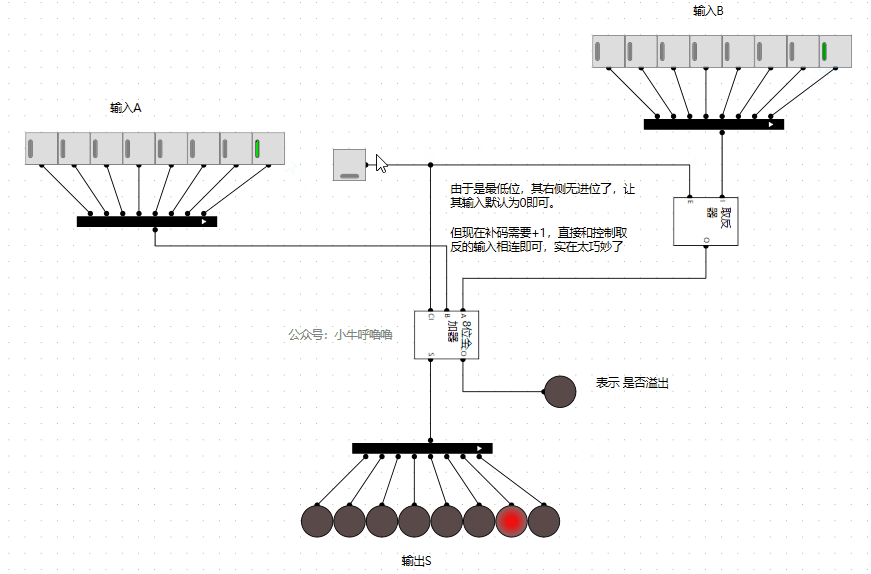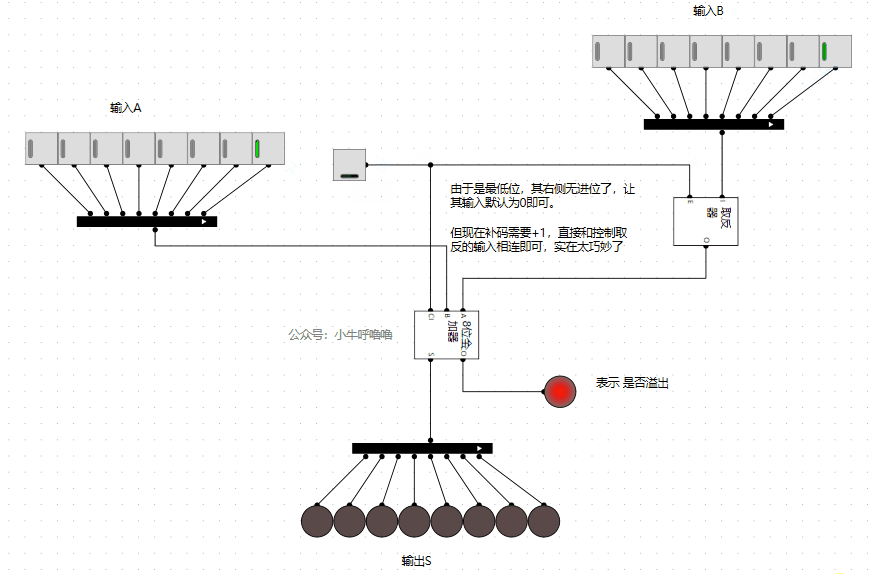
上圖計算結果,相當於:
1+1 =2
1-1 =0
但是上面有個問題是,1-1=0時,雖然燈泡是0,但是旁邊的溢位標誌顯示溢位了,我們還需改造一下。我們這裡簡單地,就直接讓減法不溢位即可(這種處理方式還是比較粗暴的,但是實現起來比較簡單)
我們來寫出溢位輸入IY,是否取反輸入IF(如果取反,就代表是減法操作),溢位輸出O的真值表關係
| IY | IF | O |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
我們可以推出公式:O=非IF * IY,所以需要非門和與門
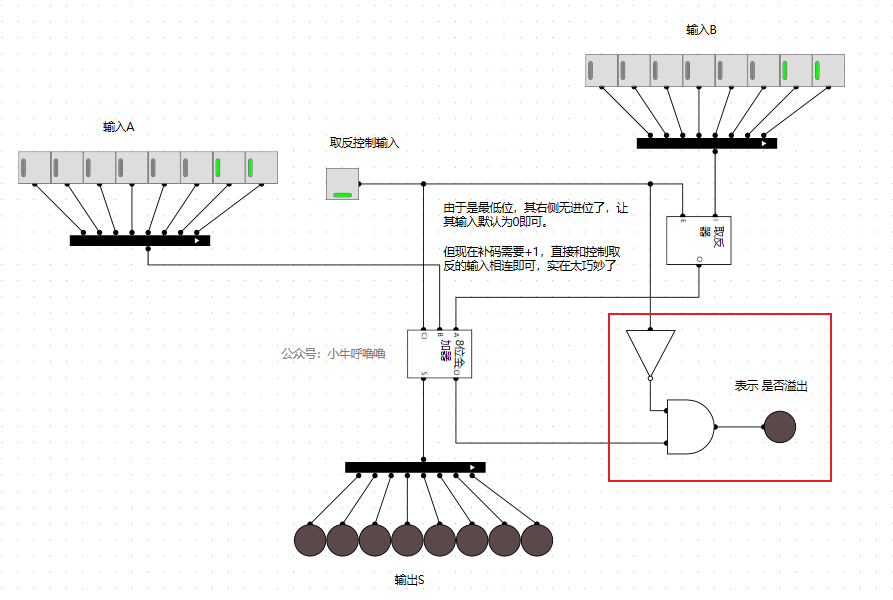
這樣就減法時,就不會溢位了。但其實這個加法器只能做正數的減法(也就是輸入A得大於等於輸入B),如果最後結果為負數的,還是有bug的。我們後面有機會再優化
7段數碼管16進位制顯示
由於用燈泡表示二進位制,每次得出的結果,還要我們去換算成10進位制,非常不直觀,我們接下來利用數碼管,來將二進位制數"翻譯"成10進位制數。
我們這邊利用的是7段數碼管來實現的,數碼管其實就是多個LED燈,不同的位控制不同的LED。從第0位到第7位,通過控制不同的LED來組合出數位。第7位比較特殊,數碼管顯示的是點
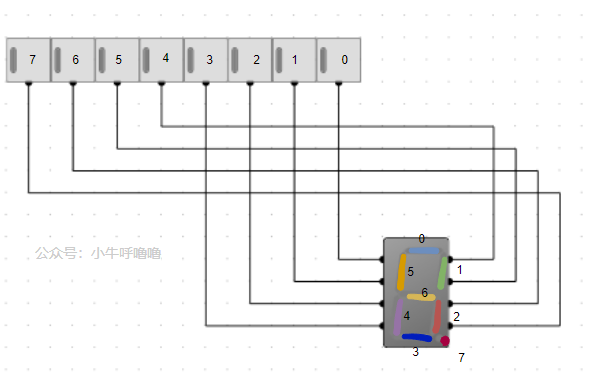
我們用上面的電路,一一將0~F16個數顯示出來,各個開關的情況記錄成下面的表:
| 數值 | 開關(2進位制) | HEX(16進位制) |
|---|---|---|
| 0 | 0011 1111 | 0x3F |
| 1 | 0011 0000 | 0x06 |
| 2 | 0101 1011 | 0x5B |
| 3 | 0100 1111 | 0x4F |
| 4 | 0110 0110 | 0x66 |
| 5 | 0110 1101 | 0x6D |
| 6 | 0111 1101 | 0x7D |
| 7 | 0000 0111 | 0x07 |
| 8 | 0111 1111 | 0x7F |
| 9 | 0110 1111 | 0x6F |
| A | 0111 0111 | 0x77 |
| b | 0111 1100 | 0x7C |
| C | 0011 1001 | 0x39 |
| D | 0101 1100 | 0x5E |
| E | 0111 1001 | 0x79 |
| F | 0111 0001 | 0x71 |
這其實就是7段數碼管的共陰極對照表,還有共陽極對照表這裡我們就不展示了。
如果直接用組合電路來封裝8位元輸入,7段數碼管的16進位制顯示,的確是可以的,但如果是16位元,32位元,64位元輸入,電路會異常的複雜,我們這邊用儲存器ROM來實現這個功能
ROM唯讀記憶體,是以非破壞性讀出方式工作,它非易失性記憶體,當電源被移除時,其資料內容不會被擦除,它還有個特點就是只能讀出而不能寫入資訊,其所存的資料,一般是裝入整機前事先寫好的,整機工作過程中只能讀出。
需要注意的是: 雖然ROM和硬碟有一些共性,但不能簡單地說ROM就是硬碟
常常與ROM相比的還有一個RAM(隨機存取記憶體),也就是我們常說的主記憶體,是與CPU直接交換資料的內部記憶體,它的特點:隨機存取、資料易失、對靜電敏感、存取速度快、需要重新整理。RAM在斷電以後儲存在上面的資料會自動消失
我們使用ROM和7段數碼管來顯示16進位制的數0~F,選用地址位寬為4,資料位寬為8,只需把對應的資料提前寫入對應的地址中即可。
這裡需要注意一下,為什麼我們選用地址位寬為4,資料位寬為8的ROM?
首先我們需要明白(1111 1111)2 = (f f)16, 7段數碼管可以表示0~F 16進位制數,我們可以用2個7段數碼管並聯將8位元二進位制數譯碼成16進位制數。
我們就先考慮1個7段數碼管和ROM的關係,單個"f"也就是第16個數,也就是說4位元二進位制,即4位元輸入,最大值為16
- 地址位寬為4, 可以保證定址2^4=16,分別對應十六進位制下的0~F
- 資料位寬為8,相當於2個7段數碼管,一個7段數碼管需要4位元輸入,2個就是8位元輸入
我們想顯示16進位制數,0~F,我們需要4位元二進位制輸入,其最大值1111,就是16(F),結合上面的共陰極對照表,我們就能總結下面的表:
| A3 | A2 | A1 | A0 | Number | HEX(16進位制) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0x3F |
| 0 | 0 | 0 | 1 | 1 | 0x06 |
| 0 | 0 | 1 | 0 | 2 | 0x5B |
| 0 | 0 | 1 | 1 | 3 | 0x4F |
| 0 | 1 | 0 | 0 | 4 | 0x66 |
| 0 | 1 | 0 | 1 | 5 | 0x6D |
| 0 | 1 | 1 | 0 | 6 | 0x7D |
| 0 | 1 | 1 | 1 | 7 | 0x07 |
| 1 | 0 | 0 | 0 | 8 | 0x7F |
| 1 | 0 | 0 | 1 | 9 | 0x6F |
| 1 | 0 | 1 | 0 | A | 0x77 |
| 1 | 0 | 1 | 1 | b | 0x7C |
| 1 | 1 | 0 | 0 | C | 0x39 |
| 1 | 1 | 0 | 1 | d | 0x5E |
| 1 | 1 | 1 | 0 | E | 0x79 |
| 1 | 1 | 1 | 1 | F | 0x71 |
根據對應關係,我們把電路和記憶體相應地址資料預先填進去
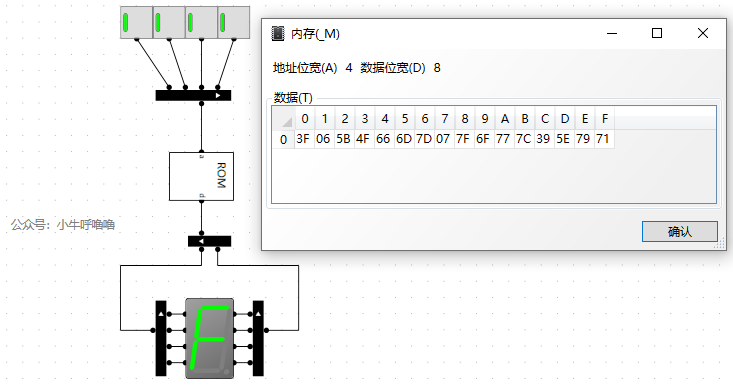
我們啟動模擬看下效果:
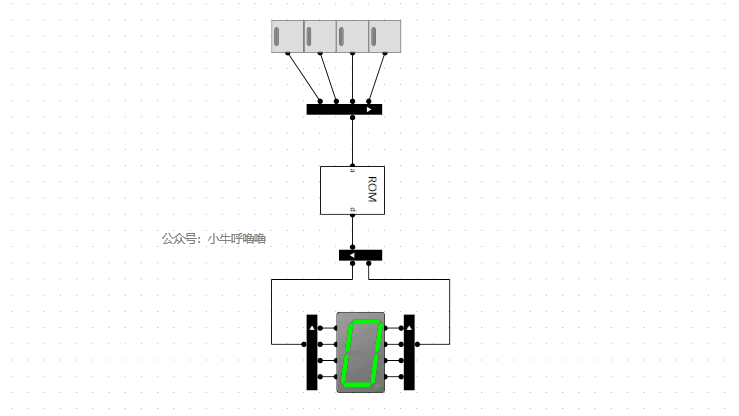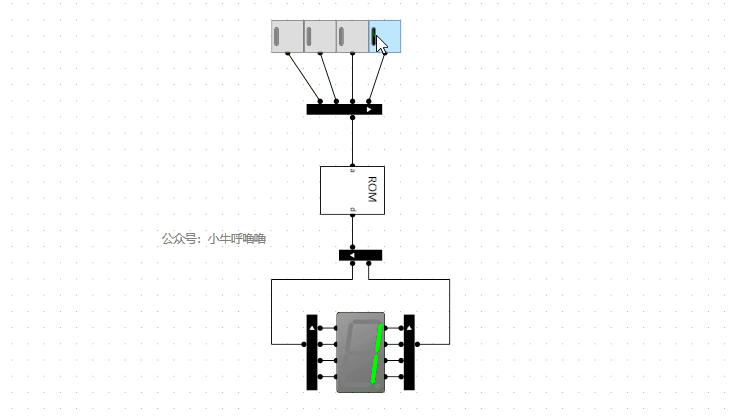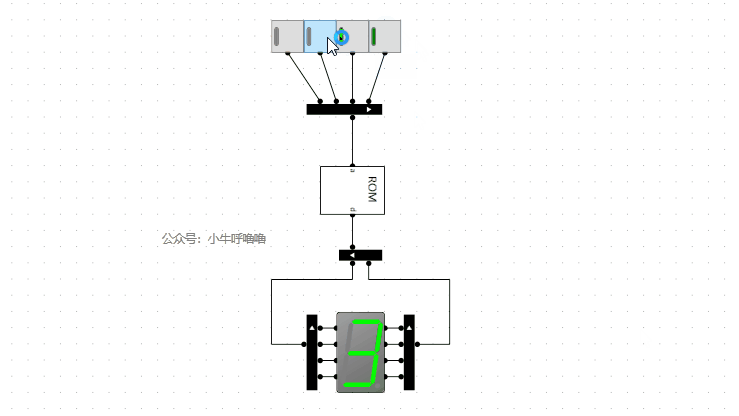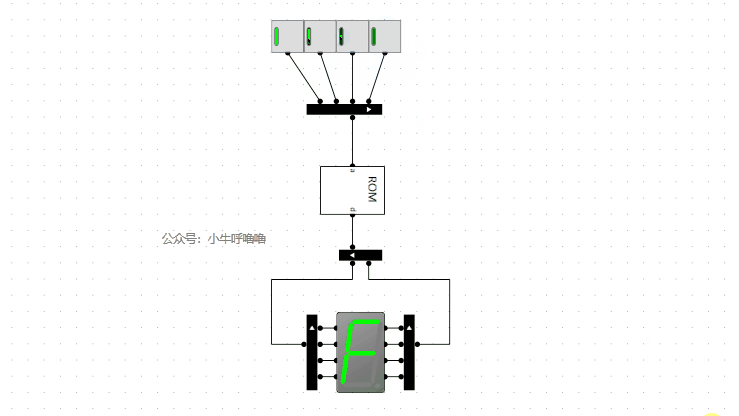
測試完成後,將4個開關換成4位元輸入。接著我們將2個4位元16進位制譯碼器並聯,就成了8位元16進位制譯碼器,並封裝一下:
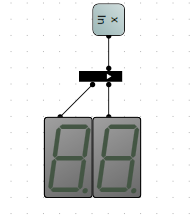
並將它與上文的全加器與減法器結合起來:
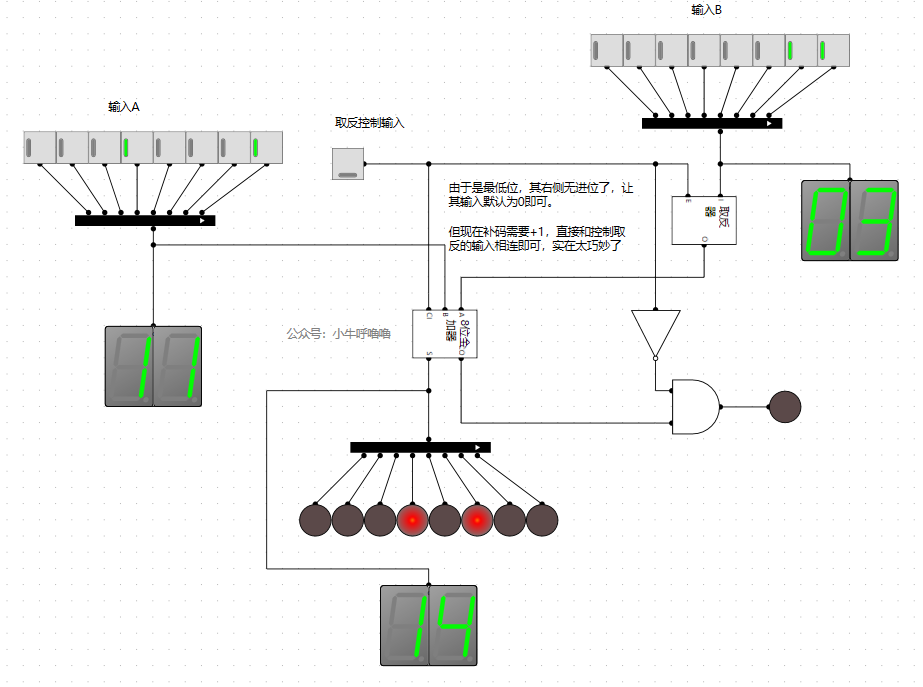
nice!
7段數碼管10進位制顯示
通過上一小節,我們成功把8位元二進位制數,"翻譯"成16進位制數,但距離我們更熟悉的十進位制還是有點距離的,我們本小節繼續改進7段數碼管,實現10進位制的譯碼
由於(1111 1111)2 = (255)10, 最大值為255
ROM需要8位元地址位寬,2^8 = 256,確保能夠將256個數(0 ~255)全部找到;255是3位數,我們至少需要3個數碼管(也就是我們上一小節封裝的4位元16進位制譯碼管),1個數碼管需要4位元輸入,所以ROM數碼管的資料位寬為12
更多精彩文章在公眾號「小牛呼嚕嚕」
電路實現:我們可以使用8個開關,來表示8位元輸入;選用8位元地址位寬且資料位寬為12的ROM,通過8位元3針腳的分線器和3個4位元16進位制譯碼管相連即可。
由於ROM的查詢表有255個數,不能像之前一樣一個個手動填寫,我們可以利用Python來實現(電腦中需要有Python3的環境)。
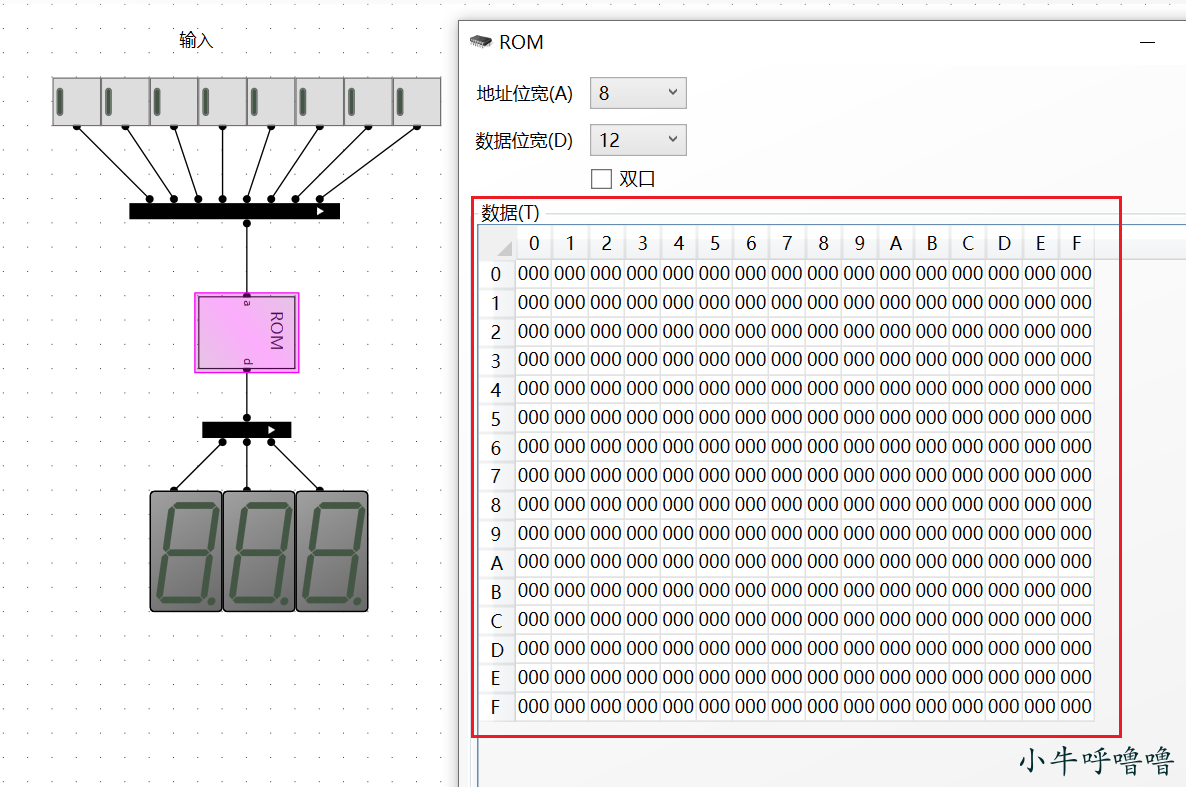
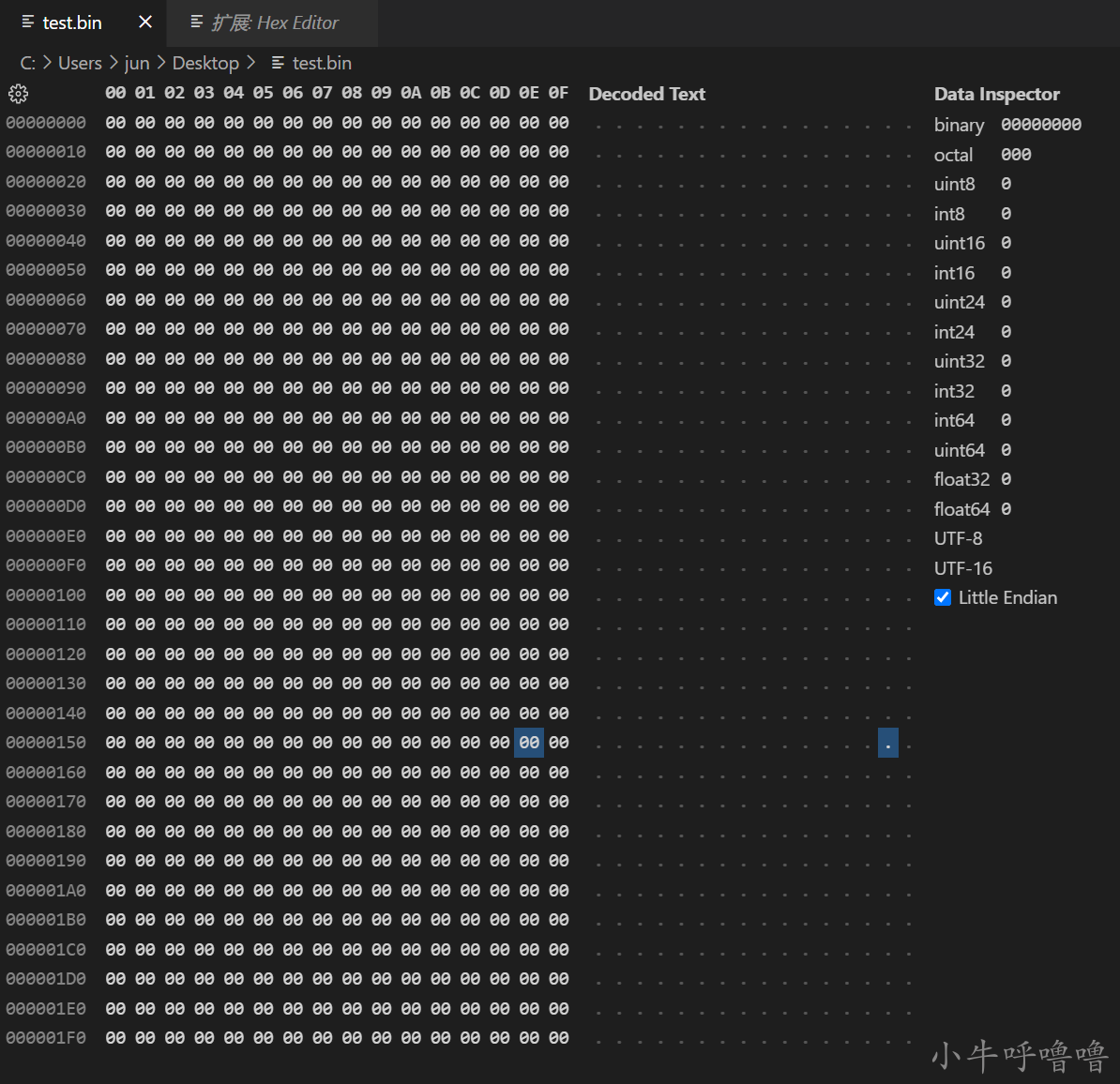
將其另存到桌面上為test.bin檔案,用vscode開啟該檔案(需要安裝 hex editor外掛來顯示二進位制),以小端顯示:
test.py:
with open('test.bin', 'wb') as f:
for i in range(256):
var = str(i)
var = int(var, base=16) //先轉成16進位制
byte = var.to_bytes(2, byteorder='little')// 再轉化成二進位制,以顯示小端
print(byte)
f.write(byte)
將其放到test.bin 同級目錄後,直接執行命令python test,py後,test.bin就變成了:
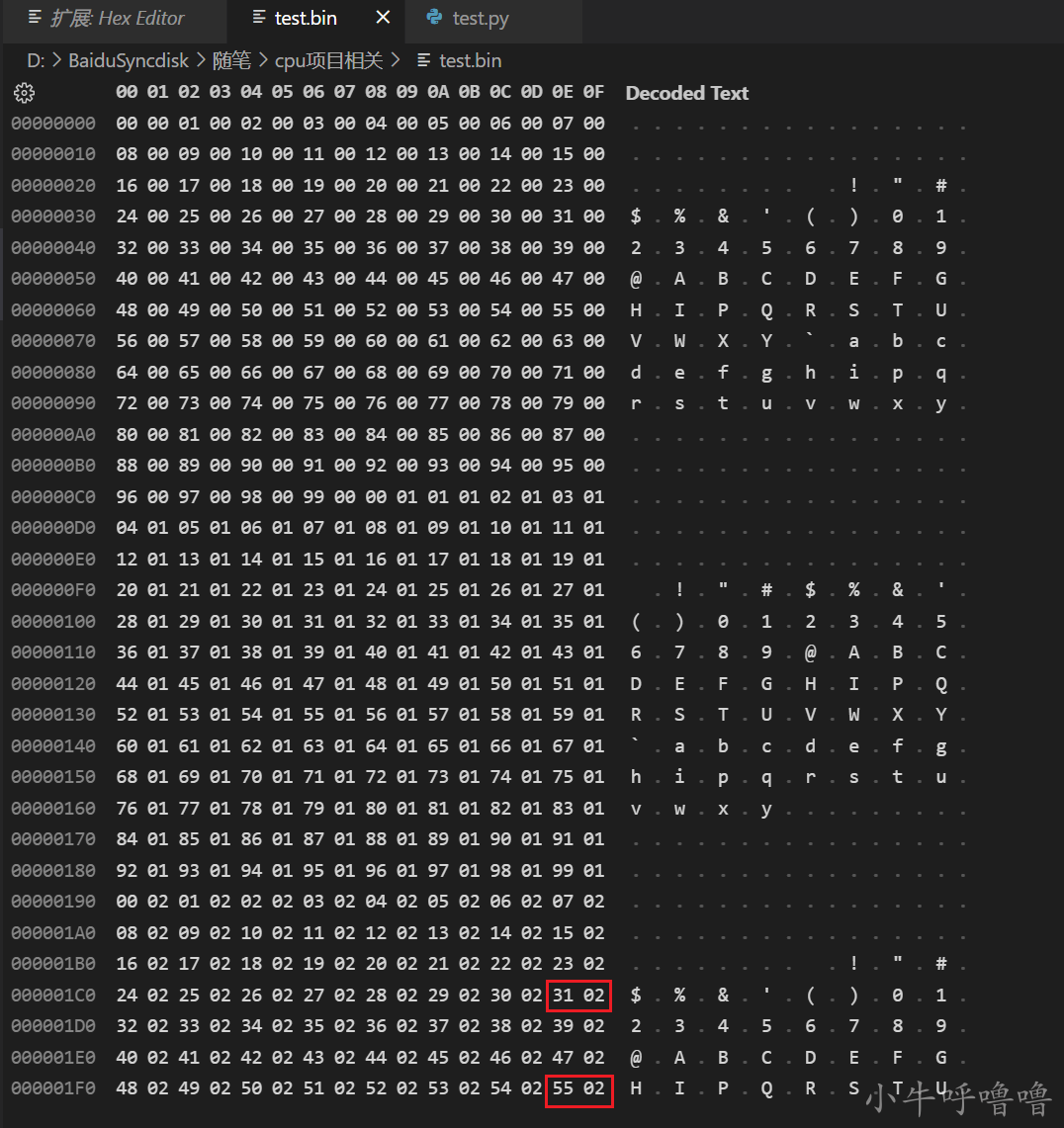
這種55 02 其實是 255,31 02 為 231 , 像這種55 02 就是小端表示法。
將test.bin 重新載入到ROM中
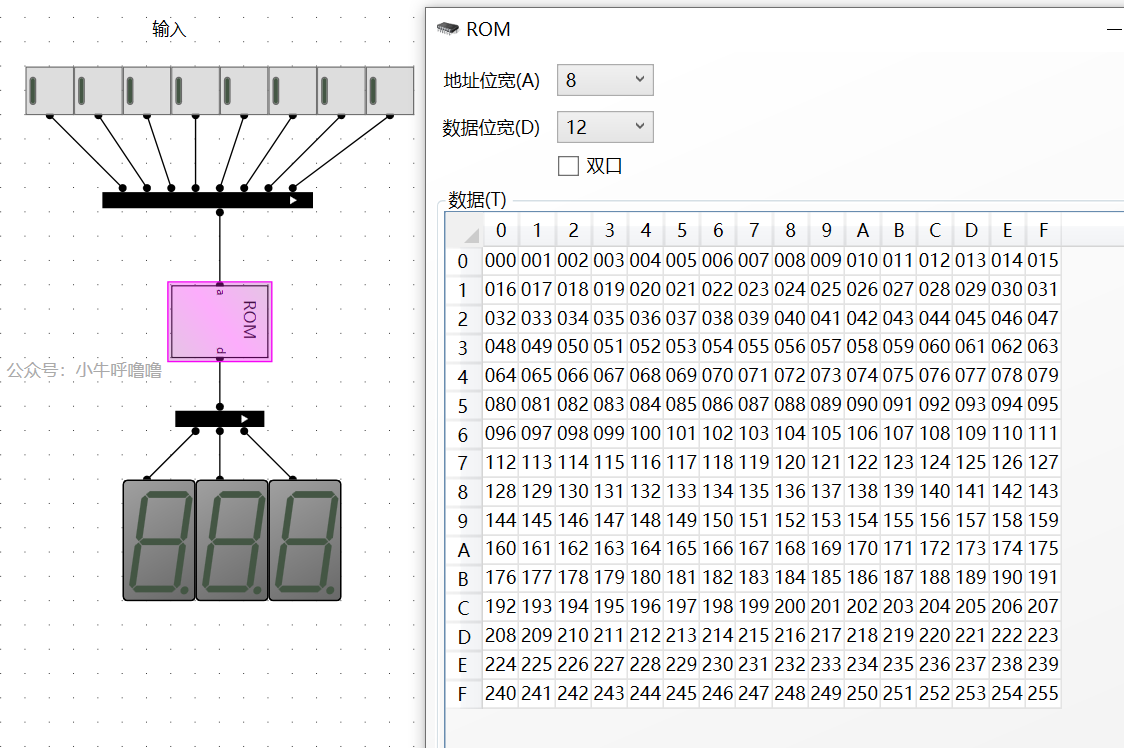
我們來啟動模擬看看:
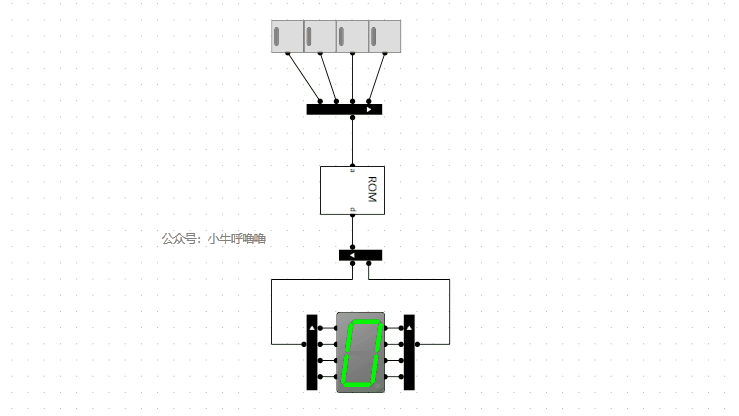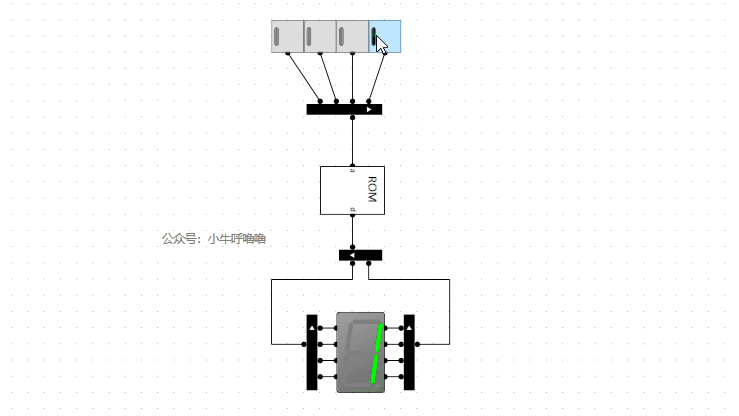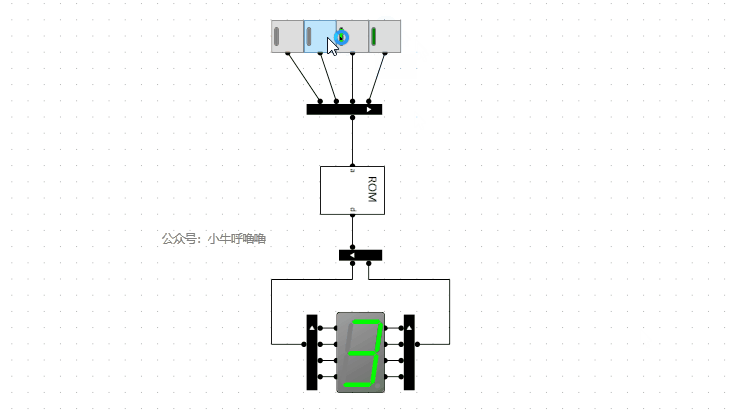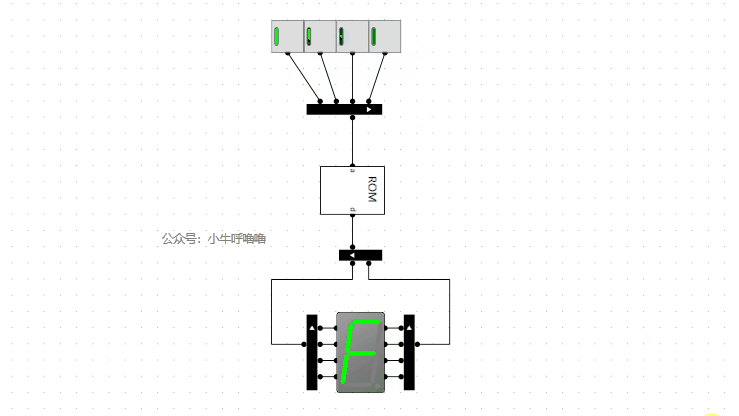
我們將輸入替換開關,然後封裝成8位元10進位制譯碼器電路,接上之前的減法器的電路:
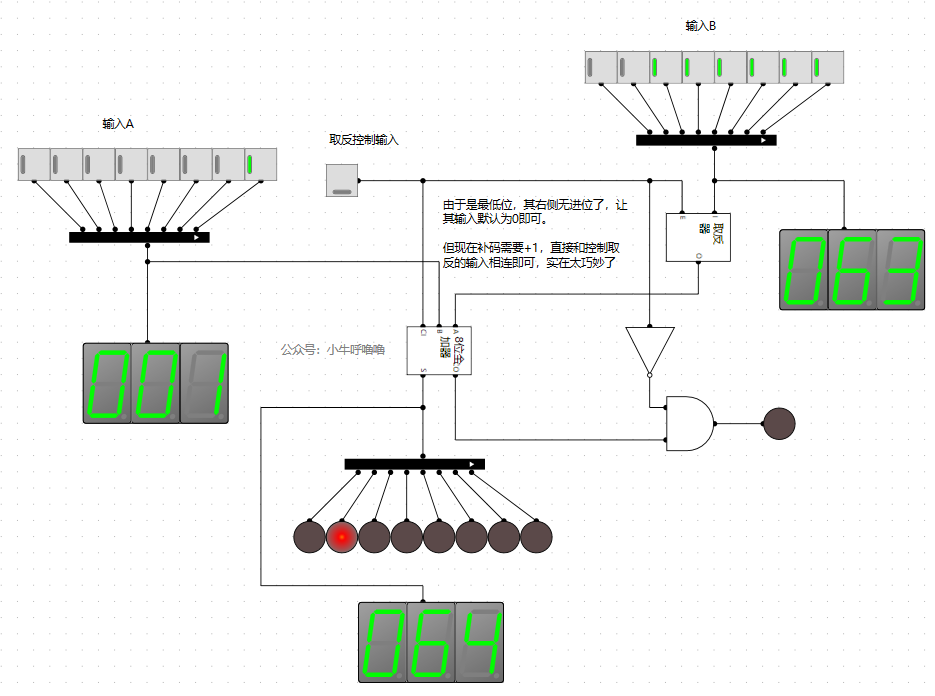
21選擇器 增強 10進位制顯示
我們現在有個需求,001,前面的0不想要,就想要1,我們藉助21選擇器來實現 高位為零時,數碼管不亮
我們先來看一下1位21選擇器,首先有2個輸入,分別為A和B,以及一個有效位EN,一個輸出S。我們的目的是實現:有效輸出A,無效輸出B。根據目的我們可以寫出真值表:
| EN | A | B | S |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
我們可以得出公式 S = EN與A + 非EN與B,進而可以畫出電路圖
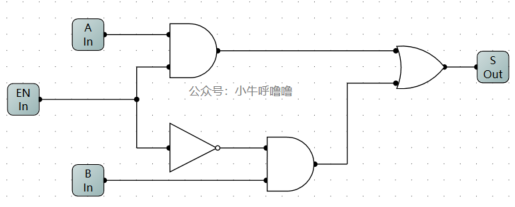
封裝後,模擬一下:
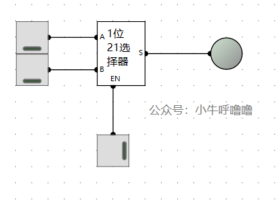
我們繼續畫出8位元21選擇器,只需將8個1位21選擇器組合在一起:
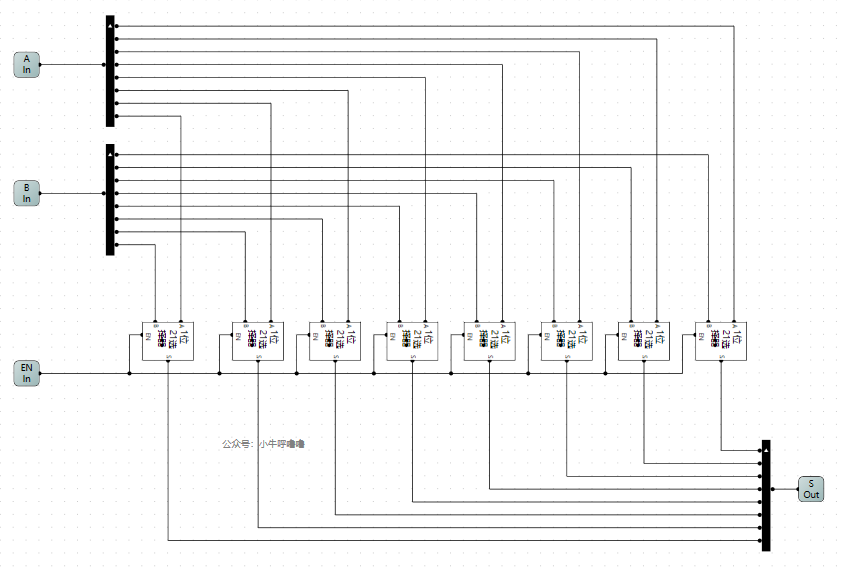
將其封裝一下,接著模擬測試:
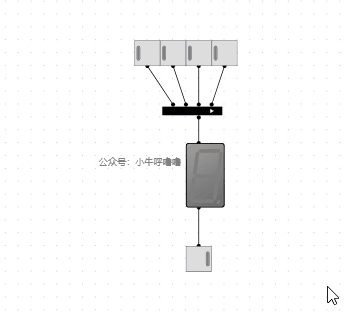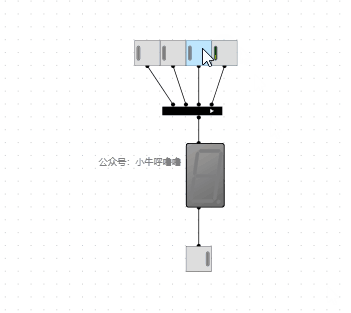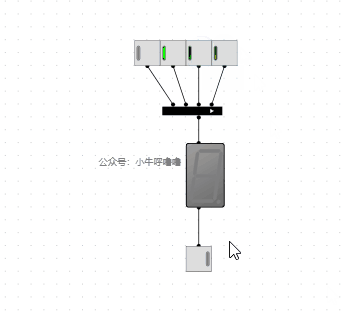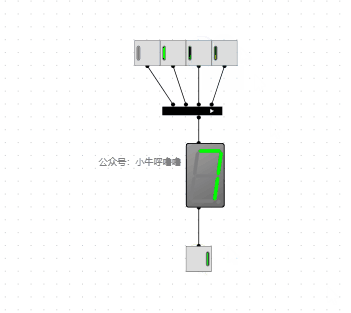
7段數碼管10進位制顯示增強的電路,我們再重新設計一下:
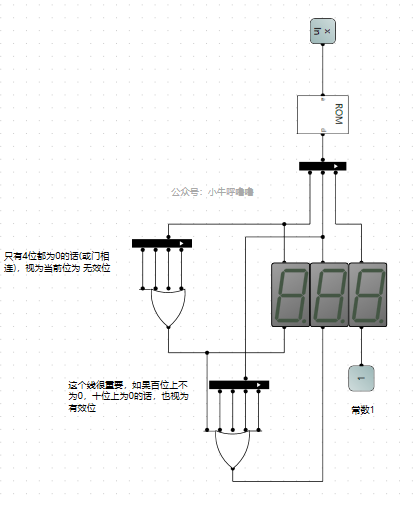
更多精彩文章在公眾號「小牛呼嚕嚕」
最後把其封裝一下,放到減法器和加法器的電路中,演示一下:
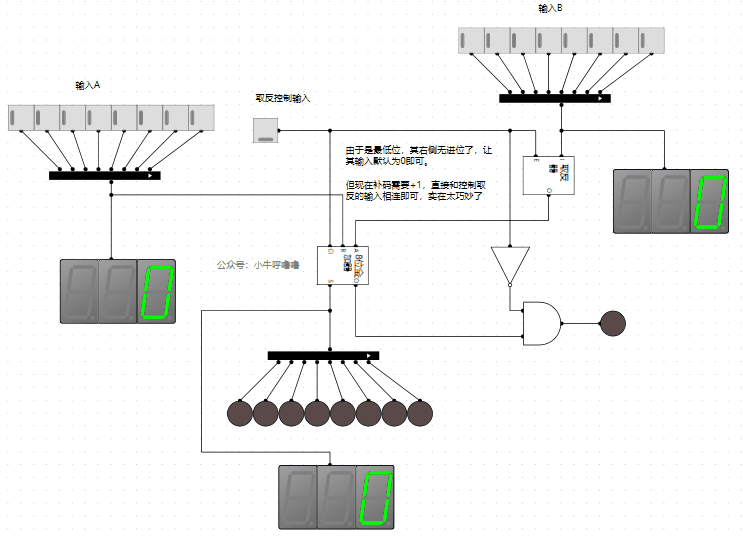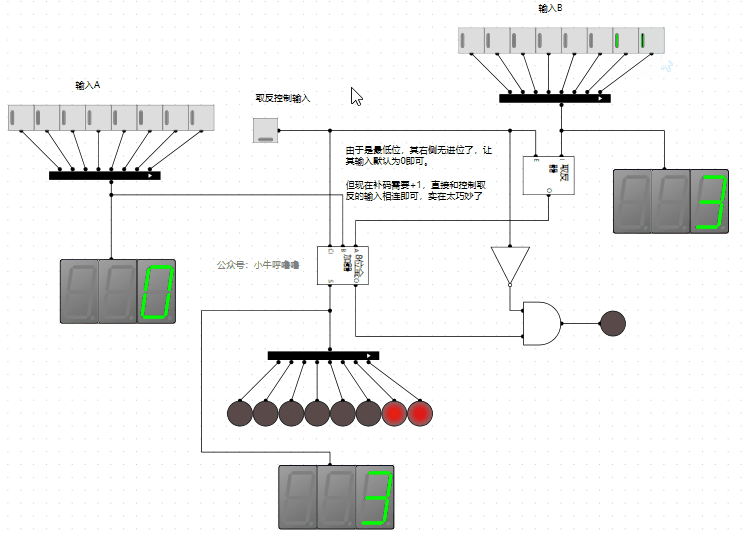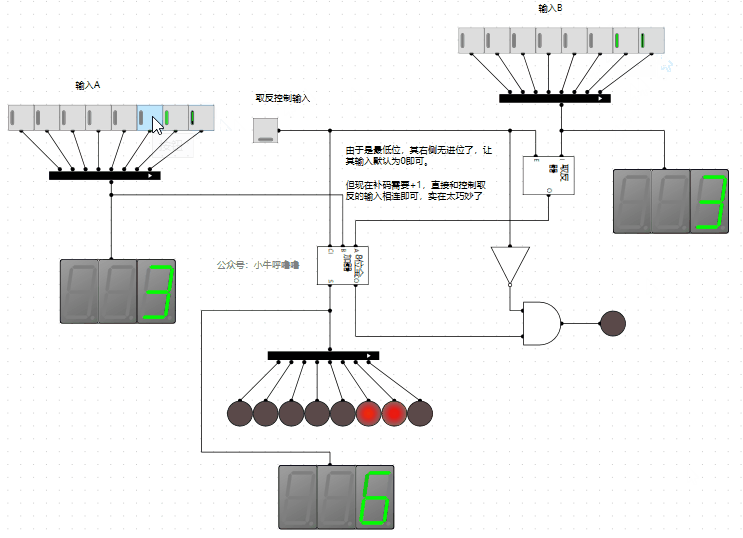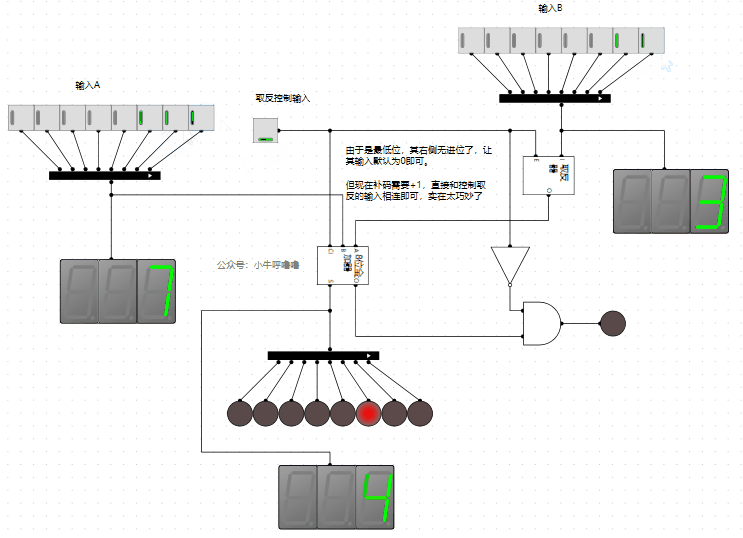
完美,這樣就實現了我們的目的。
尾語
本文我們將上一小篇文章中的簡易加法器進行來改進,通過二補數,讓加法器也是運算減法。接著為了讓我們觀察結果更加方便,我們使用了7段數碼管實現了 16進位制、10進位制顯示,最終優化了10進位制顯示,使其只顯示有效位的數值。
本系列到目前為止主要是組合邏輯電路的相關知識,後續我們會探究時序邏輯電路的奧祕,來看看開關究竟是如何實現CPU除計算功能外另一個重要的功能"記憶功能"。
參考資料:
- 一個8位元二進位制CPU的設計和實現,躊躇月光
- 《編碼:隱匿在計算機軟硬體背後的語言》
- 《穿越計算機的迷霧》
- 深入淺出計算機組成原理,徐文浩
- 執行記憶體,百度百科
全文完,感謝您的閱讀,如果我的文章對你有所幫助的話,還請點個免費的贊,你的支援會激勵我輸出更高質量的文章,感謝!
原文映象:https://mp.weixin.qq.com/s/QXWm-s-v3VuYV7s4-uE7yA
計算機內功、原始碼解析、科技故事、專案實戰、面試八股等更多硬核文章,首發於公眾號「小牛呼嚕嚕」,我們下期再見!
