「學習筆記」略談點分治
點分治適合處理大規模的樹上路徑資訊問題。
引入
給定一棵 \(n\) 個點樹和一個整數 \(k\),求樹上兩點間的距離小於等於 \(k\) 的點對有多少。
對於這個題,如果我們進行 \(O_{n^3}\) 搜尋,那隻要 \(n\) 一大,鐵定超時。
所以,我們要用一個更優秀的解法,這就是我們的點分治。
澱粉質可好吃了
變數
typedef pair<int, int> pii;
const int N = 4e4 + 10;
int n, k, rt, ans, sum;
int siz[N], maxp[N], dis[N], ok[N];
bool vis[N];
vector<pii> son[N];
n: 點數;
k: 限定距離;
rt: 根節點;
sum: 總結點數(找重心要用到);
siz: 子樹大小;
maxp: 最大的子樹的大小;
dis: 每個節點到根節點的距離;
ok: 棧;
vis: 標記;
son: 存圖。
過程
1. 找重心
為什麼是找重心?
其所有的子樹中最大的子樹節點數最少,在所有點中,重心是最優的選擇。
找到重心後,以重心為根開始操作。
void get_root(int u, int fat) {
siz[u] = 1;
maxp[u] = 0;
for (pii it : son[u]) {
int v = it.first;
if (v == fat || vis[v]) continue;
get_root(v, u);
siz[u] += siz[v];
maxp[u] = max(maxp[u], siz[v]);
}
maxp[u] = max(maxp[u], sum - siz[u]);
if (maxp[u] < maxp[rt]) rt = u;
}
這裡並不是很難。
2. 處理答案
對於每個根節點,我們進行搜尋,會得到每個節點到根節點的距離。
我們現在要求出經過根節點的距離小於等於 \(k\) 的點對個數。
我們將所有點的距離從小到大排一個序,設定左右兩個指標,如果左指標和右指標所指向的節點到根節點的距離小於等於 \(k\),則兩個指標之間所有的節點到左指標所指向的節點的距離都小於等於 \(k\),與此同時 l ++,如果左右指標所指向的節點的距離之和大於 \(k\),那麼右指標就要左移,即 -- r。
然後我們對每個節點都這樣搜一遍,將答案加出來,就可以輕鬆加愉快的切掉這個問題了
嗎?
考慮一下,如果是下面這種情況
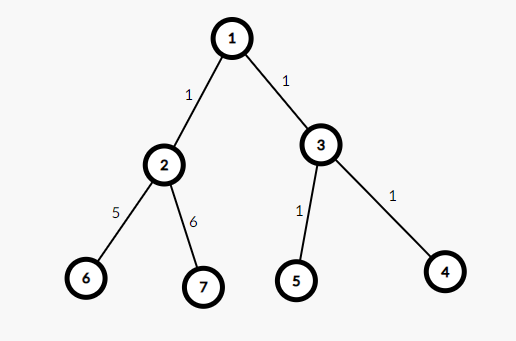
假設 \(k = 5\),那麼以 \(1\) 為根節點時,\(4\) 與 \(5\) 很顯然是符合的,我們將它加入答案。
然後,當我們又以 \(3\) 為根節點時,\(4\) 和 \(5\) 這個點對我們就又統計了一次。
有什麼問題?重複啦!
原因也很簡單,因為 \(4\) 和 \(5\) 在同一個子樹內,因此只要它們在這個大的樹內符合要求,那麼它們在它們的小子樹內也一定符合要求,那麼就一定會有重複,因此,利用容斥的原理,我們先求出總的答案,然後再減去重複的部分。
如何檢驗重複的部分呢?
我們發現它們共同經過了一條邊 \(1 - 3\),所以我們再次搜尋,這次直接初始化 dis[3] = 1,然後其他的依舊按照操作,最後如果他們的距離小於等於 \(k\),則這就是重複的部分,統計一下,最後減去即可。
減去之後,就在子樹裡找重心,設定新的根節點,開始新的答案統計,與此同時,我們要將原來的根節點打上標記,防止搜尋範圍離開了這個子樹。
(或許這就是點「分治」的所在,搜完一個重心後,相當於把這個重心刪除,然後就將一顆樹分成多個互相之間沒有聯絡的小子樹,各自進行搜尋)
int calc(int u, int val) {
ok[0] = 0;
dis[u] = val;
dfs(u, 0);
sort(ok + 1, ok + ok[0] + 1);
int cnt = 0, l = 1, r = ok[0];
while (l < r) {
if (ok[l] + ok[r] <= k) {
cnt += (r - l ++);
}
else {
r --;
}
}
return cnt;
}
void work(int u) {
ans += calc(u, 0);
vis[u] = 1;
for (pii it : son[u]) {
int v = it.first, w = it.second;
if (vis[v]) continue;
ans -= calc(v, w);
maxp[rt = 0] = sum = siz[v];
get_root(v, 0);
work(rt);
}
}
關於 sum = siz[v];,當我們再次找重心時,是要在這個子樹中找重心,不能超出這個子樹,因此要將總個數也設為 siz[v]。
3. 處理到根節點的距離
這個,應該就沒什麼好說的了。
void dfs(int u, int fat) {
ok[++ ok[0]] = dis[u];
siz[u] = 1;
for (pii it : son[u]) {
int v = it.first, w = it.second;
if (v == fat || vis[v]) continue;
dis[v] = dis[u] + w;
dfs(v, u);
siz[u] += siz[v];
}
}
看到這,你已經看完了點分治的核心步驟,讓我們把程式碼整合一下,去切掉這道模板題 Tree。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 4e4 + 10;
int n, k, rt, ans, sum;
int siz[N], maxp[N], dis[N], ok[N];
bool vis[N];
vector<pii> son[N];
inline ll read() {
ll x = 0;
int fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
void get_root(int u, int fat) {
siz[u] = 1;
maxp[u] = 0;
for (pii it : son[u]) {
int v = it.first;
if (v == fat || vis[v]) continue;
get_root(v, u);
siz[u] += siz[v];
maxp[u] = max(maxp[u], siz[v]);
}
maxp[u] = max(maxp[u], sum - siz[u]);
if (maxp[u] < maxp[rt]) rt = u;
}
void dfs(int u, int fat) {
ok[++ ok[0]] = dis[u];
siz[u] = 1;
for (pii it : son[u]) {
int v = it.first, w = it.second;
if (v == fat || vis[v]) continue;
dis[v] = dis[u] + w;
dfs(v, u);
siz[u] += siz[v];
}
}
int calc(int u, int val) {
ok[0] = 0;
dis[u] = val;
dfs(u, 0);
sort(ok + 1, ok + ok[0] + 1);
int cnt = 0, l = 1, r = ok[0];
while (l < r) {
if (ok[l] + ok[r] <= k) {
cnt += (r - l ++);
}
else {
r --;
}
}
return cnt;
}
void work(int u) {
ans += calc(u, 0);
vis[u] = 1;
for (pii it : son[u]) {
int v = it.first, w = it.second;
if (vis[v]) continue;
ans -= calc(v, w);
maxp[rt = 0] = sum = siz[v];
get_root(v, 0);
work(rt);
}
}
int main() {
n = read();
for (int i = 1, u, v, w; i < n; ++ i) {
u = read(), v = read(), w = read();
son[u].push_back({v, w});
son[v].push_back({u, w});
}
k = read();
maxp[rt = 0] = sum = n;
get_root(1, 0);
work(rt);
printf("%d\n", ans);
return 0;
}
其他題目
模板題(大霧)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, ll> pil;
const int N = 1e4 + 5;
int n, m, sum, rt;
int q[N], siz[N], maxs[N], can[N], dis[N];
int tp[N];
bool ok[N], vis[N];
vector<pil> son[N];
bool cmp(int x, int y) {
return dis[x] < dis[y];
}
void get_root(int u, int fat, int tot) {
siz[u] = 1;
maxs[u] = 0;
for (auto [v, w] : son[u]) {
if (v == fat || vis[v]) continue;
get_root(v, u, tot);
siz[u] += siz[v];
maxs[u] = max(siz[v], maxs[u]);
}
maxs[u] = max(maxs[u], tot - siz[u]);
if (!rt || maxs[u] < maxs[rt]) {
rt = u;
}
}
void dfs(int u, int fat, int d, int from) {
can[++ can[0]] = u;
dis[u] = d;
tp[u] = from;
for (auto [v, w] : son[u]) {
if (v == fat || vis[v]) continue;
dfs(v, u, d + w, from);
}
}
void calc(int u) {
can[0] = 0;
can[++ can[0]] = u;
dis[u] = 0;
tp[u] = u;
for (auto [v, w] : son[u]) {
if (vis[v]) continue;
dfs(v, u, w, v);
}
sort(can + 1, can + can[0] + 1, cmp);
for (int i = 1; i <= m; ++ i) {
int l = 1, r = can[0];
if (ok[i]) continue;
while (l < r) {
if (dis[can[l]] + dis[can[r]] > q[i]) {
r --;
}
else if (dis[can[l]] + dis[can[r]] < q[i]) {
++ l;
}
else if (tp[can[l]] == tp[can[r]]) {
if (dis[can[r]] == dis[can[r - 1]]) {
-- r;
}
else ++ l;
}
else {
ok[i] = true;
break;
}
}
}
}
void work(int u) {
vis[u] = true;
calc(u);
for (auto [v, w] : son[u]) {
if (vis[v]) continue;
rt = 0;
get_root(v, 0, siz[v]);
work(rt);
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for (int i = 1, x, y, z; i < n; ++ i) {
cin >> x >> y >> z;
son[x].push_back({y, z});
son[y].push_back({x, z});
}
for (int i = 1; i <= m; ++ i) {
cin >> q[i];
if (!q[i]) ok[i] = 1;
}
maxs[0] = n;
get_root(1, 0, n);
work(rt);
for (int i = 1; i <= m; ++ i) {
if (ok[i]) {
cout << "AYE" << '\n';
}
else {
cout << "NAY" << '\n';
}
}
return 0;
}