Python從0到1丨瞭解影象形態學運算中腐蝕和膨脹
摘要:這篇文章將詳細講解影象形態學知識,主要介紹影象腐蝕處理和膨脹處理。
本文分享自華為雲社群《[Python從零到壹] 四十七.影象增強及運算篇之腐蝕和膨脹詳解》,作者: eastmount 。
一.形態學理論知識
數學形態學的應用可以簡化影象資料,保持它們基本的形狀特徵,並出去不相干的結構。數學形態學的演演算法有天然的並行實現的結構,主要針對的是二值影象(0或1)。在影象處理方面,二值形態學經常應用到對影象進行分割、細化、抽取骨架、邊緣提取、形狀分析、角點檢測,分水嶺演演算法等。由於其演演算法簡單,演演算法能夠並行運算所以經常應用到硬體中[1-2]。
常見的影象形態學運算包括:
- 腐蝕
- 膨脹
- 開運算
- 閉運算
- 梯度運算
- 頂帽運算
- 底帽運算
這些運算在OpenCV中主要通過MorphologyEx()函數實現,它能利用基本的膨脹和腐蝕技術,來執行更加高階形態學變換,如開閉運算、形態學梯度、頂帽、黑帽等,也可以實現最基本的影象膨脹和腐蝕。其函數原型如下:
- dst = cv2.morphologyEx(src, model, kernel)
– src表示原始影象
– model表示影象進行形態學處理,包括:
(1)cv2.MORPH_OPEN:開運算(Opening Operation)
(2)cv2.MORPH_CLOSE:閉運算(Closing Operation)
(3)cv2.MORPH_GRADIENT:形態學梯度(Morphological Gradient)
(4)cv2.MORPH_TOPHAT:頂帽運算(Top Hat)
(5)cv2.MORPH_BLACKHAT:黑帽運算(Black Hat) - kernel表示折積核,可以用numpy.ones()函數構建
二.影象腐蝕
影象的腐蝕(Erosion)和膨脹(Dilation)是兩種基本的形態學運算,主要用來尋找影象中的極小區域和極大區域。影象腐蝕類似於「領域被蠶食」,它將影象中的高亮區域或白色部分進行縮減細化,其執行結果比原圖的高亮區域更小。
設A,B為集合,A被B的腐蝕,記為A-B,其定義為:
該公式表示影象A用折積模板B來進行腐蝕處理,通過模板B與影象A進行折積計算,得出B覆蓋區域的畫素點最小值,並用這個最小值來替代參考點的畫素值。如圖1所示,將左邊的原始影象A腐蝕處理為右邊的效果圖A-B。
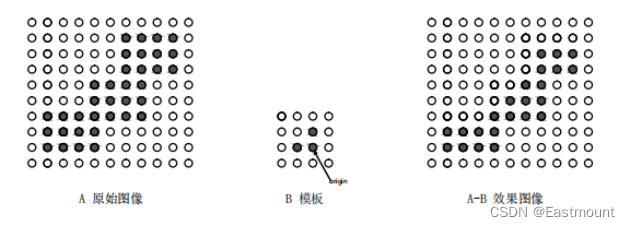
影象腐蝕主要包括二值影象和折積核兩個輸入物件,折積核是腐蝕中的關鍵陣列,採用Numpy庫可以生成。折積核的中心點逐個畫素掃描原始影象,被掃描到的原始影象中的畫素點,只有當折積核對應的元素值均為1時,其值才為1,否則將其畫素值修改為0。在Python中,主要呼叫OpenCV的erode()函數實現影象腐蝕。
其函數原型如下:
- dst = cv2.erode(src, kernel, iterations)
– src表示原始影象
– kernel表示折積核
– iterations表示迭代次數,預設值為1,表示進行一次腐蝕操作
可以採用函數numpy.ones((5,5), numpy.uint8)建立5×5的折積核,如下:

影象腐蝕操作的程式碼如下所示:
# -*- coding: utf-8 -*- # By:Eastmount import cv2 import numpy as np #讀取圖片 src = cv2.imread('test01.jpg', cv2.IMREAD_UNCHANGED) #設定折積核 kernel = np.ones((5,5), np.uint8) #影象腐蝕處理 erosion = cv2.erode(src, kernel) #顯示影象 cv2.imshow("src", src) cv2.imshow("result", erosion) #等待顯示 cv2.waitKey(0) cv2.destroyAllWindows()
輸出結果如圖2所示,左邊表示原圖,右邊是腐蝕處理後的影象,可以發現影象中的干擾細線(噪聲)被清洗乾淨。
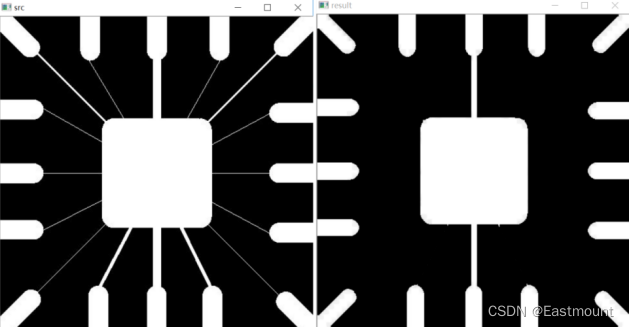
如果腐蝕之後的影象仍然存在噪聲,可以設定迭代次數進行多次腐蝕操作。比如進行9次腐蝕操作的核心程式碼如下:
- erosion = cv2.erode(src, kernel,iterations=9)
最終經過9次腐蝕處理的輸出影象如圖3所示。

三.影象膨脹
影象膨脹是腐蝕操作的逆操作,類似於「領域擴張」,它將影象中的高亮區域或白色部分進行擴張,其執行結果比原圖的高亮區域更大。
設A,B為集合,∅為空集,A被B的膨脹,記為A⊕B,其中⊕為膨脹運算元,膨脹定義為:
該公式表示用B來對影象A進行膨脹處理,其中B是一個折積模板,其形狀可以為正方形或圓形,通過模板B與影象A進行折積計算,掃描影象中的每一個畫素點,用模板元素與二值影象元素做「與」運算,如果都為0,那麼目標畫素點為0,否則為1。從而計算B覆蓋區域的畫素點最大值,並用該值替換參考點的畫素值實現影象膨脹。圖4是將左邊的原始影象A膨脹處理為右邊的效果圖A⊕B。
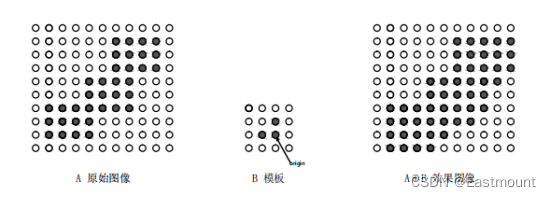
影象被腐蝕處理後,它將去除噪聲,但同時會壓縮影象,而影象膨脹操作可以去除噪聲並保持原有形狀,如圖5所示。

在Python中,主要呼叫OpenCV的dilate()函數實現影象腐蝕。函數原型如下:
- dst = cv2.dilate(src, kernel, iterations)
– src表示原始影象
– kernel表示折積核,可以用numpy.ones()函數構建
– iterations表示迭代次數,預設值為1,表示進行一次膨脹操作
影象膨脹操作的程式碼如下所示:
# -*- coding: utf-8 -*- # By:Eastmount import cv2 import numpy as np #讀取圖片 src = cv2.imread('zhiwen.png', cv2.IMREAD_UNCHANGED) #設定折積核 kernel = np.ones((5,5), np.uint8) #影象膨脹處理 erosion = cv2.dilate(src, kernel) #顯示影象 cv2.imshow("src", src) cv2.imshow("result", erosion) #等待顯示 cv2.waitKey(0) cv2.destroyAllWindows()
輸出結果如圖6所示:
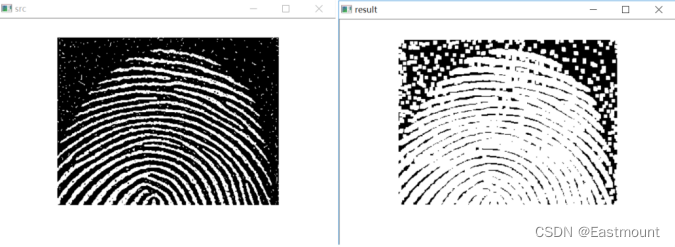
四.總結
本文主要介紹影象形態學處理,詳細講解了影象腐蝕處理和膨脹處理。數學形態學是一種應用於影象處理和圖形識別領域的新方法,其基本思想是用具有一定形態的結構元素去量度和提取影象中對應形狀以達到對影象分析和識別目的。
參考文獻:
- [1]岡薩雷斯著,阮秋琦譯. 數位影像處理(第3版)[M]. 北京:電子工業出版社,2013.
- [2]阮秋琦. 數位影像處理學(第3版)[M]. 北京:電子工業出版社,2008.
- [3]毛星雲,冷雪飛. OpenCV3程式設計入門[M]. 北京:電子工業出版社,2015.
- [4]Eastmount. [Python影象處理] 八.影象腐蝕與影象膨脹[EB/OL]. (2018-10-31). https://blog.csdn.net/Eastmount/article/details/83581277.