一些關於運籌學和機器學習之間協同作用的思考
2023-05-23 06:01:48
幾十年來,運籌學(OR)和機器學習(ML)一直作為兩個相對獨立的研究領域不斷髮展。資料科學和人工智慧領域的專家可能更熟悉機器學習而不是運籌學,儘管每個機器學習實踐者都應該至少了解一些優化技術,因為每個機器學習問題本質上都是一個優化問題。在本文中,我將把運籌學和機器學習視為一個整體話題,回顧它們之間的聯絡,並分享一些近些年這兩個領域之間協同作用的最新進展,以充分發揮兩個領域的優勢。
下面的圖示從三個方面說明了運籌學和機器學習之間的聯絡:運籌學幫助訓練機器學習模型,機器學習為運籌學提供輸入,機器學習改進運籌學的求解方法。接下來的段落將詳細闡述這三個方面。
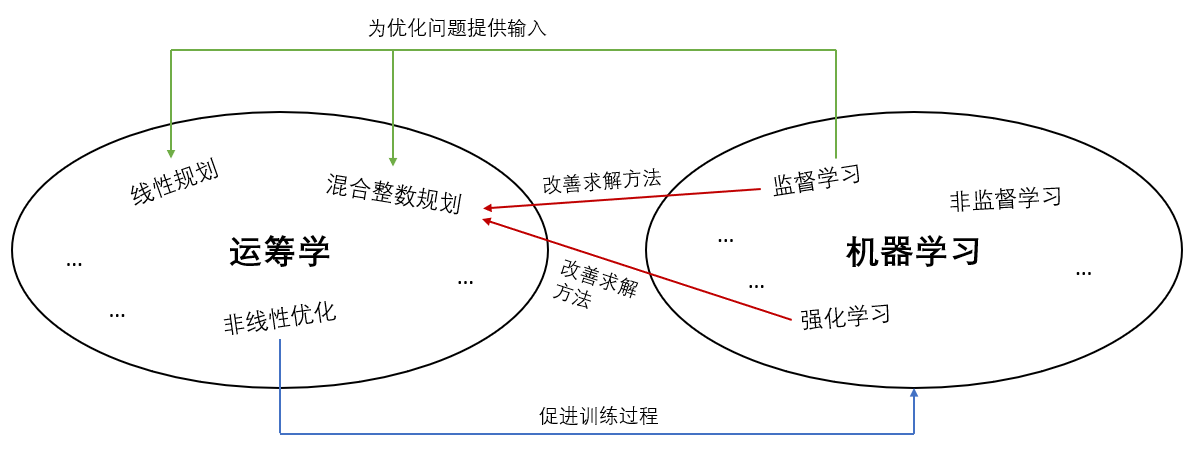
1. 運籌學幫助訓練機器學習模型
OR的核心是優化。OR學者已經開發出了許多技術來找到決策變數的最優值,以最小化或最大化優化問題的目標函數。根據優化問題是否有約束條件,優化問題可以分為有約束優化和無約束優化。根據目標函數和約束條件的形式,優化問題可以大致分為線性優化和非線性優化。
在ML中最常遇到的優化問題可能是非線性優化問題,因為在監督學習的分類任務和迴歸任務中,損失函數(例如交叉熵或均方誤差)通常相對於ML模型的引數呈非線性形式。梯度下降演演算法通常能夠有效地解決這些問題。如果存在正則化項,我們最終會得到一個帶有約束的非線性優化問題(例如嶺迴歸、LASSO、支援向量機)。在這種情況下,我們應用拉格朗日乘數並處理原始優化問題的拉格朗日鬆弛形式,這是一種典型的OR技術,用於解決複雜的約束。例如,在嶺迴歸中,我們嘗試解決以下問題:
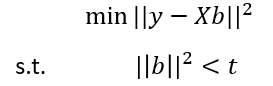
其中,y是觀測到的輸出變數的向量,X是觀測到的輸入變數的矩陣,b是要擬合的係數向量,t是用於控制正則化程度的引數。直接解決這個公式並不容易,因此我們應用拉格朗日乘數λ,將原始公式轉換為其拉格朗日鬆弛形式。
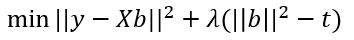
進一步化簡後變為:
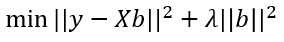
現在可以應用無約束優化技術來獲得b的最優值。
每個ML問題本質上都是一個優化問題,其中損失函數是目標函數,ML模型的引數是決策變數。在這個意義上,OR技術支ML的發展,因為更好的非線性優化問題的解決方法肯定會提高ML模型訓練過程的準確性和效率。這種OR和ML之間的相互作用如本文開頭給出的圖示中的藍色箭頭所示。
2. 機器學習為運籌學提供輸入
與OR技術在ML中的應用不同,現實世界應用中占主導地位的OR模型是線性規劃(LP)和混合整數線性規劃(MILP)模型。LP問題是一個具有線性目標函數和線性約束的優化問題,其中決策變數可以取連續值。而雖然MILP問題也具有線性目標函數和線性約束,但其中的一些決策變數必須取整數值。LP和MILP在各種行業中有廣泛的應用。例如,在供應鏈管理中,MILP通常用於設施選址、生產計劃和車輛路徑規劃等問題。這些問題通常具有線性成本函數作為目標函數,並有許多約束條件,如滿足客戶需求、確保資源的最小利用率等等。事實上,OR從業者往往不會將現實世界的問題表述為非線性優化問題,因為這些問題求解起來會更加複雜,特別是當存在許多約束條件時。
在這樣的OR應用中,主要是監督學習模型提供LP和MILP模型中已知引數的估計值。例如,在供應鏈管理領域,我們可以建立一個監督學習模型來預測客戶需求,這將成為LP和MILP模型中約束條件或目標函數中的已知引數。客戶需求的預測可以是點估計或概率估計,取決於優化問題是確定性還是隨機性。由於ML模型會影響OR應用的輸入引數的準確性,因此ML模型的質量也會影響OR應用的成功。這種OR和ML之間的互動作用由圖中的綠色箭頭表示。
下面我將通過一個簡單的設施選址問題的例子展示一個ML模型的輸出是如何被應用為MILP的輸入的。假設一家公司希望在I個候選站點中選擇建立分銷中心,向J個客戶傳送其成品。每個站點i都有不同的儲存成品的最大容量,最多為m_i個產品單位。建立每個站點i需要一定的固定建設費用f_i。從站點i運輸每個產品單位到客戶j都會產生運輸成本c_ij。每個客戶j都有需求d_j,所有客戶的需求必須得到滿足。令二進位制變數y_i表示我們是否在站點i建立設施,x_ij表示要從站點i運送到客戶j的產品數量。優化問題的目標是最小化總成本,該問題可以表示為以下形式:
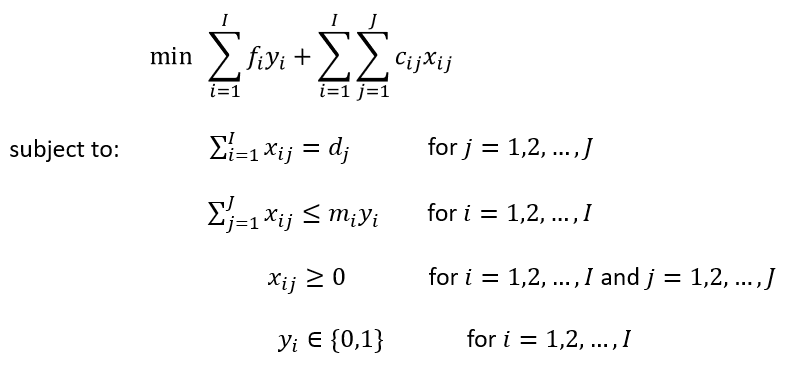
在這裡,y_i和x_ij是表示我們需要做出決策的決策變數,在我們嘗試解決問題之前是未知的。其他變數是已知引數,在我們嘗試解決問題之前必須知道。ML在這個問題中的作用是可以提供需求預測,即d_j的估計值。需求預測屬於時間序列預測的範疇,因為需求資料通常以時間序列的形式出現。可以應用各種演演算法,從傳統的時間序列模型(例如ARIMA、指數平滑等)到ML模型(例如LightGBM、神經網路)來得到d_j的準確估計。ML模型也可以用於獲得其他引數的估計,例如c_ij、f_i等,但以我個人經驗,我在需求預測方面看到的應用更多。以上優化問題可以用任何商業求解器(如CPLEX、Gurobi和FICO Xpress)和非商業求解器(如SCIP)來解決。
3. 機器學習改進了運籌學的求解方法
正如OR影響了ML的訓練過程,ML也可以在OR模型的求解過程中發揮作用。近年來,人們越來越關注使用ML來提高解決混合整數規劃(MIP)的分支定界演演算法的效率。分支定界是一種廣泛用於解決MIP的演演算法,類似於樹搜尋演演算法。假設我們正在解決一個最小化問題。在根節點處,該演演算法先求解原問題的LP鬆弛問題(在MIP中放棄整數約束可將原問題轉換為其LP鬆弛問題)。然後,該演演算法從根節點開發出兩個分支,產生兩個新節點,並使用最接近的整數向每個分支新增一個附加約束。下圖簡要說明了分支定界演演算法中開發分支的過程。
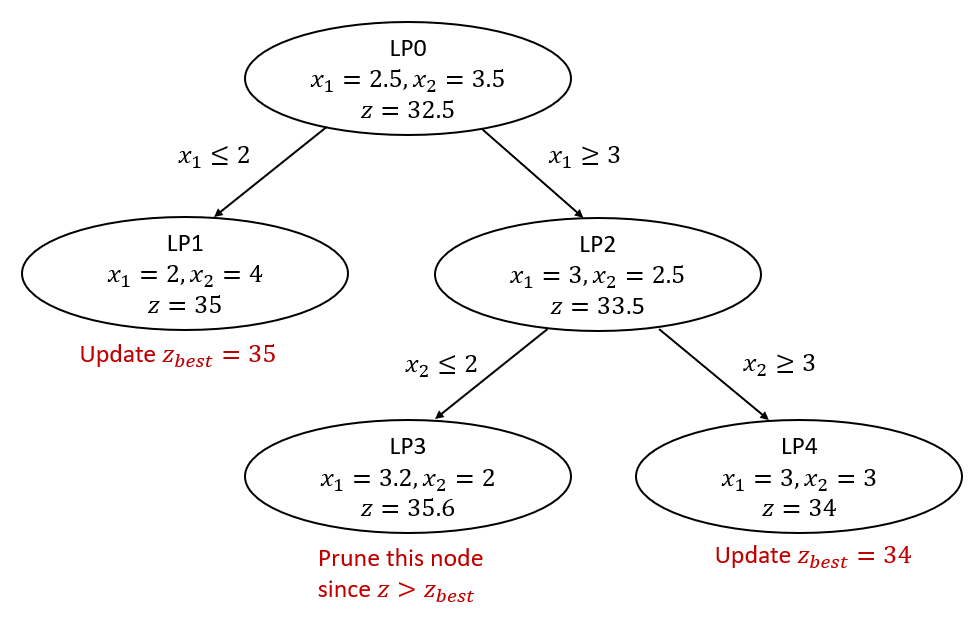
以上圖為例,如果在原問題的線性規劃鬆弛問題(即LP0)的最優解中,x_1 = 2.5,我們選擇對它進行分支,那麼我們將在第一分支中新增 x_1 ≤ 2 的限制,第二分支中新增 x_1 ≥ 3 的限制。然後,在每個新節點中,我們求解帶有新新增的約束的LP鬆弛問題。以上過程稱為分支,我們在開發樹的過程中重複此過程。在某一節點上,如果帶有整數約束的決策變數都是整數,則我們到達了一個葉節點。
請注意,在搜尋樹時,每當我們在一個節點上遇到整數解時,我們會更新當前最優解。當前最優解提供了MIP最優目標值的上界。如果在某個節點上,LP鬆弛問題的最優目標值大於當前最優解,則沒有必要進一步探索此節點,該節點將被剪枝。這樣的剪枝過程通過消除到達樹的每個葉節點的必要性,顯著減少了樹搜尋的工作量。
然而,即使進行了剪枝,實際問題通常也非常龐大,執行基本的分支定界演演算法仍然非常耗時。學者們提出了幾種改進分支定界演演算法的思路。其中一個想法是在某些節點上為LP鬆弛問題新增割平面。這些割平面可以排除非整數解,但不能排除整數解。通過在某些節點為線性鬆弛問題新增割平面,我們可以縮小線性鬆弛問題的可行域,使通過求解線性鬆弛問題找到整數解更加容易。該演演算法被稱為分支切割法。
新增割平面是一個好的想法,但有時找到好的割平面本身就是一項不容易的任務。在這種情況下,對某些節點應用啟發式演演算法是尋找整數解非常有用的方法。其中一個常用的啟發式演演算法是鬆弛導向鄰域搜尋(relaxation induced neighborhood search)。這種啟發式演演算法檢視當前最佳整數解和當前節點的LP鬆弛問題的非整數解,固定這兩個解中取值一致的決策變數的值,再將其餘決策變數作為子MIP求解。
在分支界定法中,每個整數解都為原始MIP提供了最優解的一個上界(假設我們解決一個最小化問題),而在活性節點上(未被剪枝的節點)的線性鬆弛問題的每個非整數解都是原始MIP最優解的一個下界。因此,新增割平面有助於改善最優解的下界,應用啟發式方法有助於改善最優解的上界,這兩者共同幫助分支定界演演算法更快地收斂。
回到OR和ML之間的相互作用,利用ML改進分支定界法的核心思想是將ML應用於:
1. 學習分支——即在節點上選擇哪個決策變數進行分支,
2. 學習如何切割——即如何找到有效的約束條件新增到LP鬆弛問題中,
3. 學習如何找到好的啟發式方法 - 幫助找到更好的整數解,
4. 學習如何設定優化求解器的引數——如何設定求解器(例如,終止準則,應用啟發式演演算法的頻率),以便更快地解決問題。
我們通常需要一個大型的MIP問題範例集來訓練ML模型,然後該ML模型將把其學到的應用於特定MIP問題範例。
利用ML來幫助求解MIP問題是一個新興的研究領域,大部分工作集中在理論研究方面,而不是在商業或非商業MIP求解器中進行實際實現。可通過以下一些有用的資源,進一步瞭解這一領域。
1. ML4CO是一個與此領域相關的比賽,旨在鼓勵參賽者使用ML解決組合優化(與整數規劃概念類似)問題。該比賽設定了三個任務:原始任務、對偶任務和設定任務,每個任務專注於分支定界演演算法的不同方面。假設我們求解一個最小化MIP問題,原始任務要求參與者使用ML在根節點找到更好的整數解,以降低最優解的上界。對偶任務要求參與者關注如何使用ML進行分支決策,以增加最優解的下界。最後,在設定任務中,參賽者嘗試使用ML為非商業求解器SCIP找到更好的引數設定,以解決MIP問題。
2. 「Machine Learning for Combinatorial Optimization: a Methodological Tour d’Horizon」 這篇論文對利用ML技術來解決組合優化問題的嘗試進行了概述。作者總結了使用ML解決組合優化問題的兩個動機:從專家給出的示範中學習,在搜尋最優解的過程當中以做出決策(例如分支決策);從經驗中學習,從而探索如何制定新的決策(例如分支決策)以推進最新技術。第一個概念符合模仿學習,而第二個概念更符合強化學習。本文開頭給出的圖示中的紅色箭頭展現了OR和ML之間這方面的相互作用。
3. 另一篇值得注意的論文是由Google DeepMind團隊撰寫的 「Solving Mixed Integer Programs Using Neural Networks」。該論文建立了一個MIP的圖表示,並使用神經網路生成整數變數的部分賦值和學習如何做出分支決策。該論文在提高分支定界法的效率方面取得了有希望的結果。
在本文中,我從三個方面介紹了OR和ML之間的聯絡。雖然前兩個方面已經有了成熟的技術在實際實現中,但是最後一個方面儘管非常有前途,仍然需要更多的研究努力來進行實際的可延伸的實現。OR和ML在本質上是密切相關的,並且隨著兩個領域的發展,兩者將攜手前進。也許將來還會有其他更有趣和令人興奮的OR和ML之間的協同作用。
(本文由作者譯自作者本人在Towards Data Science平臺上發表的英文部落格 「Some Thoughts on Synergies between Operations Research and Machine Learning" https://link.medium.com/RyIRzTxb0zb。歡迎關注作者的Medium平臺賬號以閱讀有關運籌學與機器學習的最新英文部落格。)