資料探勘實踐（金融風控）：金融風控之貸款違約預測挑戰賽（上篇）[xgboots/lightgbm/Catboost等模型]--模型融合：stacking、blending

1.賽題簡介

賽題以金融風控中的個人信貸為背景，要求選手根據貸款申請人的資料資訊預測其是否有違約的可能，以此判斷是否通過此項貸款，這是一個典型的分類問題。通過這道賽題來引導大家瞭解金融風控中的一些業務背景，解決實際問題，幫助競賽新人進行自我練習、自我提高。

賽題以預測金融風險為任務，資料集報名後可見並可下載，該資料來自某信貸平臺的貸款記錄，總資料量超過120w，包含47列變數資訊，其中15列為匿名變數。為了保證比賽的公平性，將會從中抽取80萬條作為訓練集，20萬條作為測試集A，20萬條作為測試集B，同時會對employmentTitle、purpose、postCode和title等資訊進行脫敏。

比賽地址：https://tianchi.aliyun.com/competition/entrance/531830/introduction

專案連結以及碼源見文末

1.1資料介紹

賽題以預測使用者貸款是否違約為任務，資料集報名後可見並可下載，該資料來自某信貸平臺的貸款記錄，總資料量超過120w，包含47列變數資訊，其中15列為匿名變數。為了保證比賽的公平性，將會從中抽取80萬條作為訓練集，20萬條作為測試集A，20萬條作為測試集B，同時會對employmentTitle、purpose、postCode和title等資訊進行脫敏。

一般而言，對於資料在比賽介面都有對應的資料概況介紹（匿名特徵除外），說明列的性質特徵。瞭解列的性質會有助於我們對於資料的理解和後續分析。 Tip:匿名特徵，就是未告知資料列所屬的性質的特徵列。

train.csv

• id 為貸款清單分配的唯一信用證標識
• loanAmnt 貸款金額
• term 貸款期限（year）
• interestRate 貸款利率
• installment 分期付款金額
• grade 貸款等級
• subGrade 貸款等級之子級
• employmentTitle 就業職稱
• employmentLength 就業年限（年）
• homeOwnership 借款人在登記時提供的房屋所有權狀況
• annualIncome 年收入
• verificationStatus 驗證狀態
• issueDate 貸款發放的月份
• purpose 借款人在貸款申請時的貸款用途類別
• postCode 借款人在貸款申請中提供的郵政編碼的前3位數位
• regionCode 地區編碼
• dti 債務收入比
• delinquency_2years 借款人過去2年信用檔案中逾期30天以上的違約事件數
• ficoRangeLow 借款人在貸款發放時的fico所屬的下限範圍
• ficoRangeHigh 借款人在貸款發放時的fico所屬的上限範圍
• openAcc 借款人信用檔案中未結信用額度的數量
• pubRec 貶損公共記錄的數量
• pubRecBankruptcies 公開記錄清除的數量
• revolBal 信貸週轉餘額合計
• revolUtil 迴圈額度利用率，或借款人使用的相對於所有可用迴圈信貸的信貸金額
• totalAcc 借款人信用檔案中當前的信用額度總數
• initialListStatus 貸款的初始列表狀態
• applicationType 表明貸款是個人申請還是與兩個共同借款人的聯合申請
• earliesCreditLine 借款人最早報告的信用額度開立的月份
• title 借款人提供的貸款名稱
• policyCode 公開可用的策略_程式碼=1新產品不公開可用的策略_程式碼=2
• n系列匿名特徵 匿名特徵n0-n14，為一些貸款人行為計數特徵的處理

1.2預測指標

競賽採用AUC作為評價指標。AUC（Area Under Curve）被定義為 ROC曲線 下與座標軸圍成的面積。

1.2.1 分類演演算法常見的評估指標如下：

1、混淆矩陣（Confuse Matrix）

• （1）若一個範例是正類，並且被預測為正類，即為真正類TP(True Positive )
• （2）若一個範例是正類，但是被預測為負類，即為假負類FN(False Negative )
• （3）若一個範例是負類，但是被預測為正類，即為假正類FP(False Positive )
• （4）若一個範例是負類，並且被預測為負類，即為真負類TN(True Negative )

2、準確率（Accuracy）
準確率是常用的一個評價指標，但是不適合樣本不均衡的情況。
$Accuracy = \frac{TP + TN}{TP + TN + FP + FN}$

3、精確率（Precision）
又稱查準率，正確預測為正樣本（TP）佔預測為正樣本(TP+FP)的百分比。
$Precision = \frac{TP}{TP + FP}$

4、召回率（Recall）
又稱為查全率，正確預測為正樣本（TP）佔正樣本(TP+FN)的百分比。
$Recall = \frac{TP}{TP + FN}$

5、F1 Score
精確率和召回率是相互影響的，精確率升高則召回率下降，召回率升高則精確率下降，如果需要兼顧二者，就需要精確率、召回率的結合F1 Score。
$F1-Score = \frac{2}{\frac{1}{Precision} + \frac{1}{Recall}}$

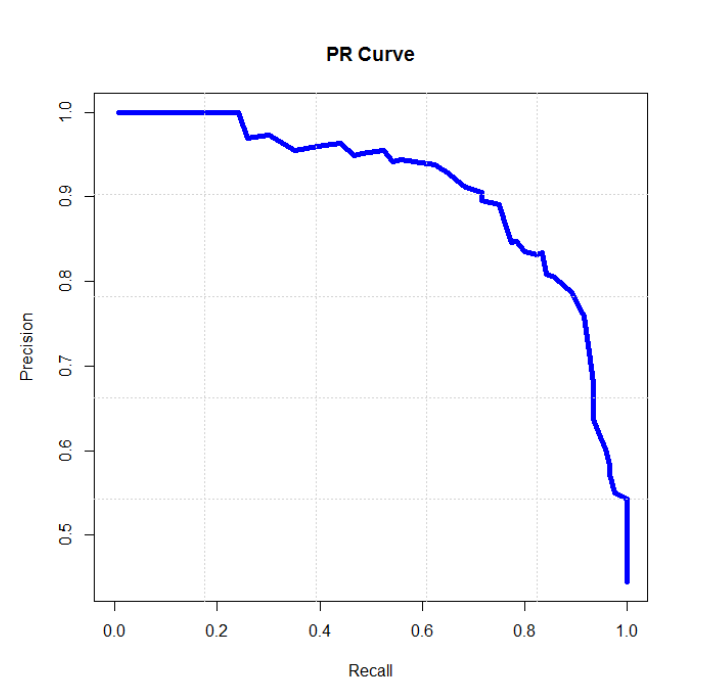
6、P-R曲線（Precision-Recall Curve）
P-R曲線是描述精確率和召回率變化的曲線

7、ROC（Receiver Operating Characteristic）

• ROC空間將假正例率（FPR）定義為 X 軸，真正例率（TPR）定義為 Y 軸。

TPR：在所有實際為正例的樣本中，被正確地判斷為正例之比率。
$TPR = \frac{TP}{TP + FN}$
FPR：在所有實際為負例的樣本中，被錯誤地判斷為正例之比率。
$FPR = \frac{FP}{FP + TN}$

8、AUC(Area Under Curve)
AUC（Area Under Curve）被定義為 ROC曲線 下與座標軸圍成的面積，顯然這個面積的數值不會大於1。又由於ROC曲線一般都處於y=x這條直線的上方，所以AUC的取值範圍在0.5和1之間。AUC越接近1.0，檢測方法真實性越高;等於0.5時，則真實性最低，無應用價值。

1.2.2 對於金融風控預測類常見的評估指標如下:

1、KS(Kolmogorov-Smirnov)
KS統計量由兩位蘇聯數學家A.N. Kolmogorov和N.V. Smirnov提出。在風控中，KS常用於評估模型區分度。區分度越大，說明模型的風險排序能力（ranking ability）越強。
K-S曲線與ROC曲線類似，不同在於

• ROC曲線將真正例率和假正例率作為橫縱軸
• K-S曲線將真正例率和假正例率都作為縱軸，橫軸則由選定的閾值來充當。
  公式如下：
  $KS=max(TPR-FPR)$
  KS不同代表的不同情況，一般情況KS值越大，模型的區分能力越強，但是也不是越大模型效果就越好，如果KS過大，模型可能存在異常，所以當KS值過高可能需要檢查模型是否過擬合。以下為KS值對應的模型情況，但此對應不是唯一的，只代表大致趨勢。

KS（%）	好壞區分能力
20以下	不建議採用
20-40	較好
41-50	良好
51-60	很強
61-75	非常強
75以上	過於高，疑似存在問題

2、ROC

3、AUC

1.3 專案流程介紹

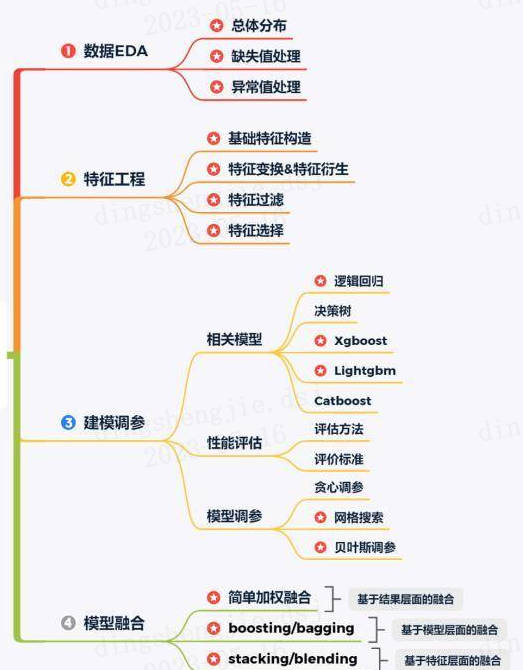
1.4 程式碼範例

本部分為對於資料讀取和指標評價的範例。

1.4.1 資料讀取pandas

import pandas as pd

train = pd.read_csv('train.csv')
testA = pd.read_csv('testA.csv')

print('Train data shape:',train.shape)
print('TestA data shape:',testA.shape)

Train data shape: (800000, 47)
TestA data shape: (200000, 48)

train.head()

1.4.2 分類指標評價計算範例

## 混淆矩陣
import numpy as np
from sklearn.metrics import confusion_matrix
y_pred = [0, 1, 0, 1]
y_true = [0, 1, 1, 0]
print('混淆矩陣:\n',confusion_matrix(y_true, y_pred))

混淆矩陣:
 [[1 1]
 [1 1]]

## accuracy
from sklearn.metrics import accuracy_score
y_pred = [0, 1, 0, 1]
y_true = [0, 1, 1, 0]
print('ACC:',accuracy_score(y_true, y_pred))

ACC: 0.5

## Precision,Recall,F1-score
from sklearn import metrics
y_pred = [0, 1, 0, 1]
y_true = [0, 1, 1, 0]
print('Precision',metrics.precision_score(y_true, y_pred))
print('Recall',metrics.recall_score(y_true, y_pred))
print('F1-score:',metrics.f1_score(y_true, y_pred))

Precision 0.5
Recall 0.5
F1-score: 0.5

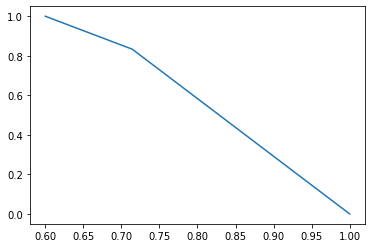
## P-R曲線
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve
y_pred = [0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
y_true = [0, 1, 1, 0, 1, 0, 1, 1, 0, 1]
precision, recall, thresholds = precision_recall_curve(y_true, y_pred)
plt.plot(precision, recall)

[<matplotlib.lines.Line2D at 0x2170d0d6108>]

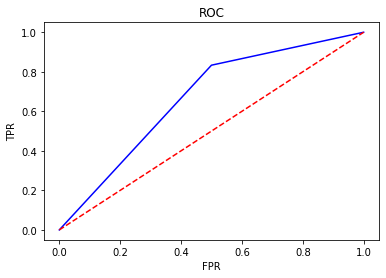
## ROC曲線
from sklearn.metrics import roc_curve
y_pred = [0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
y_true = [0, 1, 1, 0, 1, 0, 1, 1, 0, 1]
FPR,TPR,thresholds=roc_curve(y_true, y_pred)
plt.title('ROC')
plt.plot(FPR, TPR,'b')
plt.plot([0,1],[0,1],'r--')
plt.ylabel('TPR')
plt.xlabel('FPR')

Text(0.5, 0, 'FPR')

## AUC
import numpy as np
from sklearn.metrics import roc_auc_score
y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
print('AUC socre:',roc_auc_score(y_true, y_scores))

AUC socre: 0.75

## KS值 在實際操作時往往使用ROC曲線配合求出KS值
from sklearn.metrics import roc_curve
y_pred = [0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
y_true = [0, 1, 1, 0, 1, 0, 1, 1, 1, 1]
FPR,TPR,thresholds=roc_curve(y_true, y_pred)
KS=abs(FPR-TPR).max()
print('KS值：',KS)

KS值： 0.5238095238095237

1.5 拓展知識——評分卡

評分卡是一張擁有分數刻度會讓相應閾值的表。信用評分卡是用於使用者信用的一張刻度表。以下程式碼是一個非標準評分卡的程式碼流程，用於刻畫使用者的信用評分。評分卡是金融風控中常用的一種對於使用者信用進行刻畫的手段哦！

#評分卡 不是標準評分卡
def Score(prob,P0=600,PDO=20,badrate=None,goodrate=None):
    P0 = P0
    PDO = PDO
    theta0 = badrate/goodrate
    B = PDO/np.log(2)
    A = P0 + B*np.log(2*theta0)
    score = A-B*np.log(prob/(1-prob))
    return score

2.資料探索性分析

目的：

• 1.EDA價值主要在於熟悉瞭解整個資料集的基本情況（缺失值，異常值），對資料集進行驗證是否可以進行接下來的機器學習或者深度學習建模.

• 2.瞭解變數間的相互關係、變數與預測值之間的存在關係。

• 3.為特徵工程做準備

2.1 程式碼範例

2.1.1 匯入資料分析及視覺化過程需要的庫

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import datetime
import warnings
warnings.filterwarnings('ignore')

/Users/exudingtao/opt/anaconda3/lib/python3.7/site-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead.
  import pandas.util.testing as tm

以上庫都是pip install 安裝就好，如果本機有python2,python3兩個python環境傻傻分不清哪個的話,可以pip3 install 。或者直接在notebook中'!pip3 install ****'安裝。

2.1.2 讀取檔案

data_train = pd.read_csv('./train.csv')

data_test_a = pd.read_csv('./testA.csv')

• 讀取檔案的拓展知識

• pandas讀取資料時相對路徑載入報錯時，嘗試使用os.getcwd()檢視當前工作目錄。
• TSV與CSV的區別：
  • 從名稱上即可知道，TSV是用製表符（Tab,'\t'）作為欄位值的分隔符；CSV是用半形逗號（','）作為欄位值的分隔符；
  • Python對TSV檔案的支援：
    Python的csv模組準確的講應該叫做dsv模組，因為它實際上是支援正規化的分隔符分隔值檔案（DSV，delimiter-separated values）的。
    delimiter引數值預設為半形逗號，即預設將被處理檔案視為CSV。當delimiter='\t'時，被處理檔案就是TSV。
• 讀取檔案的部分（適用於檔案特別大的場景）
  • 通過nrows引數，來設定讀取檔案的前多少行，nrows是一個大於等於0的整數。
  • 分塊讀取

data_train_sample = pd.read_csv("./train.csv",nrows=5)

#設定chunksize引數，來控制每次迭代資料的大小
chunker = pd.read_csv("./train.csv",chunksize=5)
for item in chunker:
    print(type(item))
    #<class 'pandas.core.frame.DataFrame'>
    print(len(item))
    #5

檢視資料集的樣本個數和原始特徵維度

data_test_a.shape

(200000, 48)

data_train.shape

(800000, 47)

data_train.columns

Index(['id', 'loanAmnt', 'term', 'interestRate', 'installment', 'grade',
       'subGrade', 'employmentTitle', 'employmentLength', 'homeOwnership',
       'annualIncome', 'verificationStatus', 'issueDate', 'isDefault',
       'purpose', 'postCode', 'regionCode', 'dti', 'delinquency_2years',
       'ficoRangeLow', 'ficoRangeHigh', 'openAcc', 'pubRec',
       'pubRecBankruptcies', 'revolBal', 'revolUtil', 'totalAcc',
       'initialListStatus', 'applicationType', 'earliesCreditLine', 'title',
       'policyCode', 'n0', 'n1', 'n2', 'n2.1', 'n4', 'n5', 'n6', 'n7', 'n8',
       'n9', 'n10', 'n11', 'n12', 'n13', 'n14'],
      dtype='object')

檢視一下具體的列名，賽題理解部分已經給出具體的特徵含義，這裡方便閱讀再給一下：

• id 為貸款清單分配的唯一信用證標識
• loanAmnt 貸款金額
• term 貸款期限（year）
• interestRate 貸款利率
• installment 分期付款金額
• grade 貸款等級
• subGrade 貸款等級之子級
• employmentTitle 就業職稱
• employmentLength 就業年限（年）
• homeOwnership 借款人在登記時提供的房屋所有權狀況
• annualIncome 年收入
• verificationStatus 驗證狀態
• issueDate 貸款發放的月份
• purpose 借款人在貸款申請時的貸款用途類別
• postCode 借款人在貸款申請中提供的郵政編碼的前3位數位
• regionCode 地區編碼
• dti 債務收入比
• delinquency_2years 借款人過去2年信用檔案中逾期30天以上的違約事件數
• ficoRangeLow 借款人在貸款發放時的fico所屬的下限範圍
• ficoRangeHigh 借款人在貸款發放時的fico所屬的上限範圍
• openAcc 借款人信用檔案中未結信用額度的數量
• pubRec 貶損公共記錄的數量
• pubRecBankruptcies 公開記錄清除的數量
• revolBal 信貸週轉餘額合計
• revolUtil 迴圈額度利用率，或借款人使用的相對於所有可用迴圈信貸的信貸金額
• totalAcc 借款人信用檔案中當前的信用額度總數
• initialListStatus 貸款的初始列表狀態
• applicationType 表明貸款是個人申請還是與兩個共同借款人的聯合申請
• earliesCreditLine 借款人最早報告的信用額度開立的月份
• title 借款人提供的貸款名稱
• policyCode 公開可用的策略_程式碼=1新產品不公開可用的策略_程式碼=2
• n系列匿名特徵 匿名特徵n0-n14，為一些貸款人行為計數特徵的處理

通過info()來熟悉資料型別

data_train.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 800000 entries, 0 to 799999
Data columns (total 47 columns):
 #   Column              Non-Null Count   Dtype  
---  ------              --------------   -----  
 0   id                  800000 non-null  int64  
 1   loanAmnt            800000 non-null  float64
 2   term                800000 non-null  int64  
 3   interestRate        800000 non-null  float64
 4   installment         800000 non-null  float64
 5   grade               800000 non-null  object 
 6   subGrade            800000 non-null  object 
 7   employmentTitle     799999 non-null  float64
 8   employmentLength    753201 non-null  object 
 9   homeOwnership       800000 non-null  int64  
 10  annualIncome        800000 non-null  float64
 11  verificationStatus  800000 non-null  int64  
 12  issueDate           800000 non-null  object 
 13  isDefault           800000 non-null  int64  
 14  purpose             800000 non-null  int64  
 15  postCode            799999 non-null  float64
 16  regionCode          800000 non-null  int64  
 17  dti                 799761 non-null  float64
 18  delinquency_2years  800000 non-null  float64
 19  ficoRangeLow        800000 non-null  float64
 20  ficoRangeHigh       800000 non-null  float64
 21  openAcc             800000 non-null  float64
 22  pubRec              800000 non-null  float64
 23  pubRecBankruptcies  799595 non-null  float64
 24  revolBal            800000 non-null  float64
 25  revolUtil           799469 non-null  float64
 26  totalAcc            800000 non-null  float64
 27  initialListStatus   800000 non-null  int64  
 28  applicationType     800000 non-null  int64  
 29  earliesCreditLine   800000 non-null  object 
 30  title               799999 non-null  float64
 31  policyCode          800000 non-null  float64
 32  n0                  759730 non-null  float64
 33  n1                  759730 non-null  float64
 34  n2                  759730 non-null  float64
 35  n2.1                759730 non-null  float64
 36  n4                  766761 non-null  float64
 37  n5                  759730 non-null  float64
 38  n6                  759730 non-null  float64
 39  n7                  759730 non-null  float64
 40  n8                  759729 non-null  float64
 41  n9                  759730 non-null  float64
 42  n10                 766761 non-null  float64
 43  n11                 730248 non-null  float64
 44  n12                 759730 non-null  float64
 45  n13                 759730 non-null  float64
 46  n14                 759730 non-null  float64
dtypes: float64(33), int64(9), object(5)
memory usage: 286.9+ MB

總體粗略的檢視資料集各個特徵的一些基本統計量

data_train.describe()

data_train.head(3).append(data_train.tail(3))

2.1.3檢視資料集中特徵缺失值，唯一值等

檢視缺失值

print(f'There are {data_train.isnull().any().sum()} columns in train dataset with missing values.')

There are 22 columns in train dataset with missing values.

上面得到訓練集有22列特徵有缺失值，進一步檢視缺失特徵中缺失率大於50%的特徵

have_null_fea_dict = (data_train.isnull().sum()/len(data_train)).to_dict()
fea_null_moreThanHalf = {}
for key,value in have_null_fea_dict.items():
    if value > 0.5:
        fea_null_moreThanHalf[key] = value

fea_null_moreThanHalf

{}

具體的檢視缺失特徵及缺失率

#nan視覺化
missing = data_train.isnull().sum()/len(data_train)
missing = missing[missing > 0]
missing.sort_values(inplace=True)
missing.plot.bar()

<matplotlib.axes._subplots.AxesSubplot at 0x1229ab890>

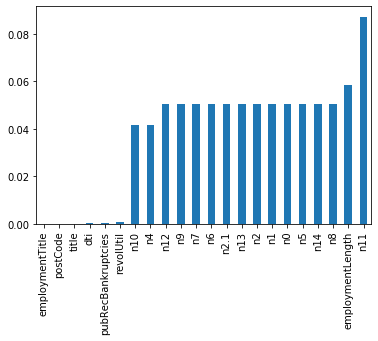
• 縱向瞭解哪些列存在 「nan」, 並可以把nan的個數列印，主要的目的在於檢視某一列nan存在的個數是否真的很大，如果nan存在的過多，說明這一列對label的影響幾乎不起作用了，可以考慮刪掉。如果缺失值很小一般可以選擇填充。
• 另外可以橫向比較，如果在資料集中，某些樣本資料的大部分列都是缺失的且樣本足夠的情況下可以考慮刪除。

Tips:
比賽大殺器lgb模型可以自動處理缺失值，Task4模型會具體學習模型瞭解模型哦！

檢視訓練集測試集中特徵屬性只有一值的特徵

one_value_fea = [col for col in data_train.columns if data_train[col].nunique() <= 1]

one_value_fea_test = [col for col in data_test_a.columns if data_test_a[col].nunique() <= 1]

one_value_fea

['policyCode']

one_value_fea_test

['policyCode']

print(f'There are {len(one_value_fea)} columns in train dataset with one unique value.')
print(f'There are {len(one_value_fea_test)} columns in test dataset with one unique value.')

There are 1 columns in train dataset with one unique value.
There are 1 columns in test dataset with one unique value.

47列資料中有22列都缺少資料，這在現實世界中很正常。‘policyCode’具有一個唯一值（或全部缺失）。有很多連續變數和一些分類變數。

2.1.4 檢視特徵的數值型別有哪些，物件型別有哪些

• 特徵一般都是由類別型特徵和數值型特徵組成，而數值型特徵又分為連續型和離散型。
• 類別型特徵有時具有非數值關係，有時也具有數值關係。比如‘grade’中的等級A，B，C等，是否只是單純的分類，還是A優於其他要結合業務判斷。
• 數值型特徵本是可以直接入模的，但往往風控人員要對其做分箱，轉化為WOE編碼進而做標準評分卡等操作。從模型效果上來看，特徵分箱主要是為了降低變數的複雜性，減少變數噪音對模型的影響，提高自變數和因變數的相關度。從而使模型更加穩定。

numerical_fea = list(data_train.select_dtypes(exclude=['object']).columns)
category_fea = list(filter(lambda x: x not in numerical_fea,list(data_train.columns)))

numerical_fea

category_fea

['grade', 'subGrade', 'employmentLength', 'issueDate', 'earliesCreditLine']

data_train.grade

0         E
1         D
2         D
3         A
4         C
         ..
799995    C
799996    A
799997    C
799998    A
799999    B
Name: grade, Length: 800000, dtype: object

• 劃分數值型變數中的連續變數和離散型變數

#過濾數值型類別特徵
def get_numerical_serial_fea(data,feas):
    numerical_serial_fea = []
    numerical_noserial_fea = []
    for fea in feas:
        temp = data[fea].nunique()
        if temp <= 10:
            numerical_noserial_fea.append(fea)
            continue
        numerical_serial_fea.append(fea)
    return numerical_serial_fea,numerical_noserial_fea
numerical_serial_fea,numerical_noserial_fea = get_numerical_serial_fea(data_train,numerical_fea)

numerical_serial_fea

numerical_noserial_fea

['term',
 'homeOwnership',
 'verificationStatus',
 'isDefault',
 'initialListStatus',
 'applicationType',
 'policyCode',
 'n11',
 'n12']

• 數值類別型變數分析

data_train['term'].value_counts()#離散型變數

3    606902
5    193098
Name: term, dtype: int64

data_train['homeOwnership'].value_counts()#離散型變數

0    395732
1    317660
2     86309
3       185
5        81
4        33
Name: homeOwnership, dtype: int64

data_train['verificationStatus'].value_counts()#離散型變數

1    309810
2    248968
0    241222
Name: verificationStatus, dtype: int64

data_train['initialListStatus'].value_counts()#離散型變數

0    466438
1    333562
Name: initialListStatus, dtype: int64

data_train['applicationType'].value_counts()#離散型變數

0    784586
1     15414
Name: applicationType, dtype: int64

data_train['policyCode'].value_counts()#離散型變數，無用，全部一個值

1.0    800000
Name: policyCode, dtype: int64

data_train['n11'].value_counts()#離散型變數，相差懸殊，用不用再分析

0.0    729682
1.0       540
2.0        24
4.0         1
3.0         1
Name: n11, dtype: int64

data_train['n12'].value_counts()#離散型變數，相差懸殊，用不用再分析

0.0    757315
1.0      2281
2.0       115
3.0        16
4.0         3
Name: n12, dtype: int64

• 數值連續型變數分析

#每個數位特徵得分佈視覺化
f = pd.melt(data_train, value_vars=numerical_serial_fea)
g = sns.FacetGrid(f, col="variable",  col_wrap=2, sharex=False, sharey=False)
g = g.map(sns.distplot, "value")

• 檢視某一個數值型變數的分佈，檢視變數是否符合正態分佈，如果不符合正太分佈的變數可以log化後再觀察下是否符合正態分佈。
• 如果想統一處理一批資料變標準化 必須把這些之前已經正態化的資料提出
• 正態化的原因：一些情況下正態非正態可以讓模型更快的收斂，一些模型要求資料正態（eg. GMM、KNN）,保證資料不要過偏態即可，過於偏態可能會影響模型預測結果。

#Ploting Transaction Amount Values Distribution
plt.figure(figsize=(16,12))
plt.suptitle('Transaction Values Distribution', fontsize=22)
plt.subplot(221)
sub_plot_1 = sns.distplot(data_train['loanAmnt'])
sub_plot_1.set_title("loanAmnt Distribuition", fontsize=18)
sub_plot_1.set_xlabel("")
sub_plot_1.set_ylabel("Probability", fontsize=15)

plt.subplot(222)
sub_plot_2 = sns.distplot(np.log(data_train['loanAmnt']))
sub_plot_2.set_title("loanAmnt (Log) Distribuition", fontsize=18)
sub_plot_2.set_xlabel("")
sub_plot_2.set_ylabel("Probability", fontsize=15)

Text(0, 0.5, 'Probability')

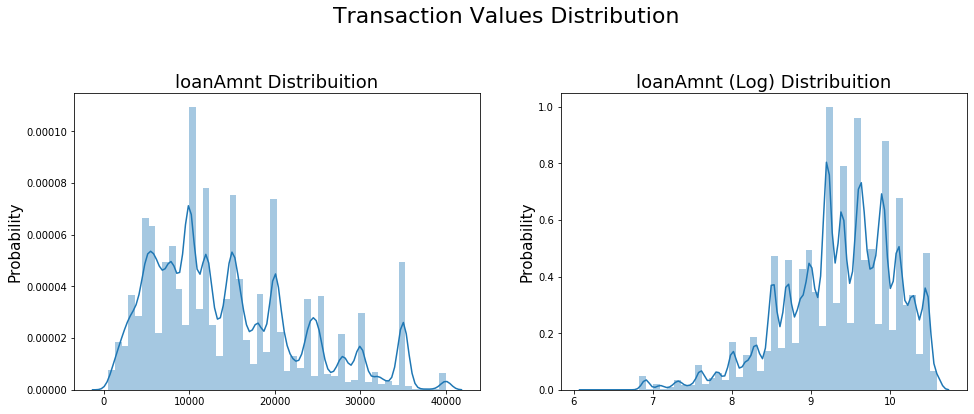
• 非數值類別型變數分析

category_fea

['grade', 'subGrade', 'employmentLength', 'issueDate', 'earliesCreditLine']

data_train['grade'].value_counts()

B    233690
C    227118
A    139661
D    119453
E     55661
F     19053
G      5364
Name: grade, dtype: int64

data_train['subGrade'].value_counts()

C1    50763
B4    49516
B5    48965
B3    48600
C2    47068
C3    44751
C4    44272
B2    44227
B1    42382
C5    40264
A5    38045
A4    30928
D1    30538
D2    26528
A1    25909
D3    23410
A3    22655
A2    22124
D4    21139
D5    17838
E1    14064
E2    12746
E3    10925
E4     9273
E5     8653
F1     5925
F2     4340
F3     3577
F4     2859
F5     2352
G1     1759
G2     1231
G3      978
G4      751
G5      645
Name: subGrade, dtype: int64

data_train['employmentLength'].value_counts()

10+ years    262753
2 years       72358
< 1 year      64237
3 years       64152
1 year        52489
5 years       50102
4 years       47985
6 years       37254
8 years       36192
7 years       35407
9 years       30272
Name: employmentLength, dtype: int64

data_train['issueDate'].value_counts()

2016-03-01    29066
2015-10-01    25525
2015-07-01    24496
2015-12-01    23245
2014-10-01    21461
              ...  
2007-08-01       23
2007-07-01       21
2008-09-01       19
2007-09-01        7
2007-06-01        1
Name: issueDate, Length: 139, dtype: int64

data_train['earliesCreditLine'].value_counts()

Aug-2001    5567
Sep-2003    5403
Aug-2002    5403
Oct-2001    5258
Aug-2000    5246
            ... 
May-1960       1
Apr-1958       1
Feb-1960       1
Aug-1946       1
Mar-1958       1
Name: earliesCreditLine, Length: 720, dtype: int64

data_train['isDefault'].value_counts()

0    640390
1    159610
Name: isDefault, dtype: int64

2.1.4 小結：

• 上面我們用value_counts()等函數看了特徵屬性的分佈，但是圖表是概括原始資訊最便捷的方式。
• 數無形時少直覺。
• 同一份資料集，在不同的尺度刻畫上顯示出來的圖形反映的規律是不一樣的。python將資料轉化成圖表，但結論是否正確需要由你保證。

2.2 變數分佈視覺化

2.2.1單一變數分佈視覺化

plt.figure(figsize=(8, 8))
sns.barplot(data_train["employmentLength"].value_counts(dropna=False)[:20],
            data_train["employmentLength"].value_counts(dropna=False).keys()[:20])
plt.show()

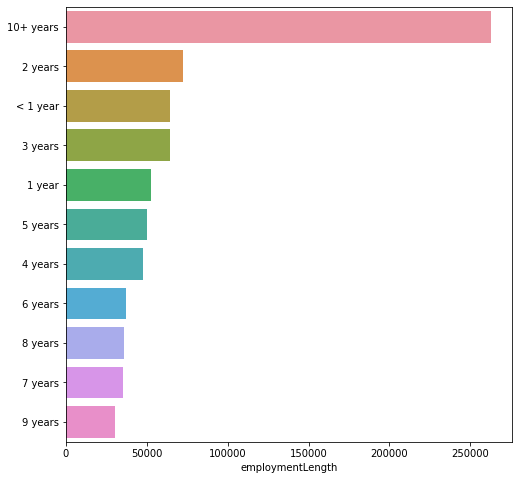
2.2.2根絕y值不同視覺化x某個特徵的分佈

• 首先檢視類別型變數在不同y值上的分佈

train_loan_fr = data_train.loc[data_train['isDefault'] == 1]
train_loan_nofr = data_train.loc[data_train['isDefault'] == 0]

fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(15, 8))
train_loan_fr.groupby('grade')['grade'].count().plot(kind='barh', ax=ax1, title='Count of grade fraud')
train_loan_nofr.groupby('grade')['grade'].count().plot(kind='barh', ax=ax2, title='Count of grade non-fraud')
train_loan_fr.groupby('employmentLength')['employmentLength'].count().plot(kind='barh', ax=ax3, title='Count of employmentLength fraud')
train_loan_nofr.groupby('employmentLength')['employmentLength'].count().plot(kind='barh', ax=ax4, title='Count of employmentLength non-fraud')
plt.show()

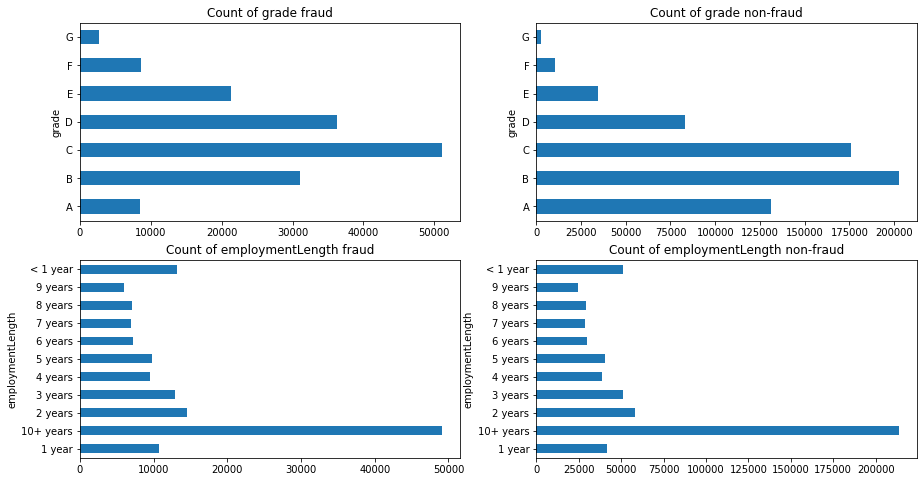
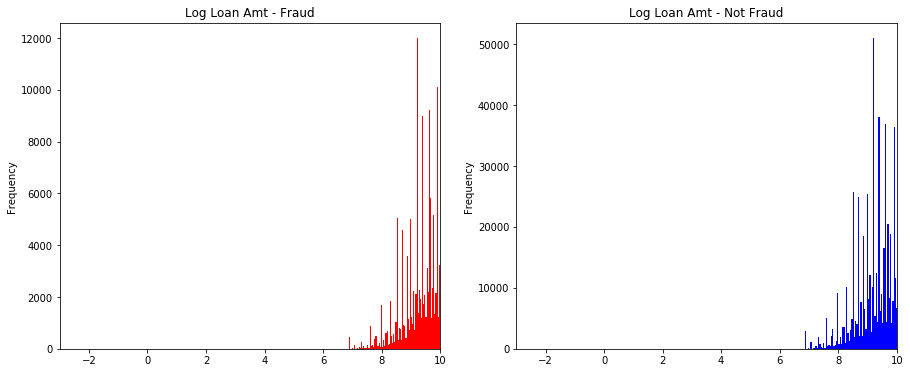
• 其次檢視連續型變數在不同y值上的分佈

fig, ((ax1, ax2)) = plt.subplots(1, 2, figsize=(15, 6))
data_train.loc[data_train['isDefault'] == 1] \
    ['loanAmnt'].apply(np.log) \
    .plot(kind='hist',
          bins=100,
          title='Log Loan Amt - Fraud',
          color='r',
          xlim=(-3, 10),
         ax= ax1)
data_train.loc[data_train['isDefault'] == 0] \
    ['loanAmnt'].apply(np.log) \
    .plot(kind='hist',
          bins=100,
          title='Log Loan Amt - Not Fraud',
          color='b',
          xlim=(-3, 10),
         ax=ax2)

<matplotlib.axes._subplots.AxesSubplot at 0x126a44b50>

total = len(data_train)
total_amt = data_train.groupby(['isDefault'])['loanAmnt'].sum().sum()
plt.figure(figsize=(12,5))
plt.subplot(121)##1代表行，2代表列，所以一共有2個圖，1代表此時繪製第一個圖。
plot_tr = sns.countplot(x='isDefault',data=data_train)#data_train‘isDefault’這個特徵每種類別的數量**
plot_tr.set_title("Fraud Loan Distribution \n 0: good user | 1: bad user", fontsize=14)
plot_tr.set_xlabel("Is fraud by count", fontsize=16)
plot_tr.set_ylabel('Count', fontsize=16)
for p in plot_tr.patches:
    height = p.get_height()
    plot_tr.text(p.get_x()+p.get_width()/2.,
            height + 3,
            '{:1.2f}%'.format(height/total*100),
            ha="center", fontsize=15) 
    
percent_amt = (data_train.groupby(['isDefault'])['loanAmnt'].sum())
percent_amt = percent_amt.reset_index()
plt.subplot(122)
plot_tr_2 = sns.barplot(x='isDefault', y='loanAmnt',  dodge=True, data=percent_amt)
plot_tr_2.set_title("Total Amount in loanAmnt  \n 0: good user | 1: bad user", fontsize=14)
plot_tr_2.set_xlabel("Is fraud by percent", fontsize=16)
plot_tr_2.set_ylabel('Total Loan Amount Scalar', fontsize=16)
for p in plot_tr_2.patches:
    height = p.get_height()
    plot_tr_2.text(p.get_x()+p.get_width()/2.,
            height + 3,
            '{:1.2f}%'.format(height/total_amt * 100),
            ha="center", fontsize=15)     

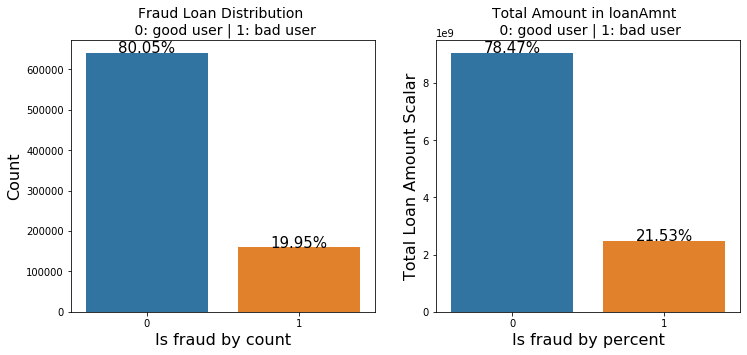
2.2.3 時間格式資料處理及檢視

#轉化成時間格式  issueDateDT特徵表示資料日期離資料集中日期最早的日期（2007-06-01）的天數
data_train['issueDate'] = pd.to_datetime(data_train['issueDate'],format='%Y-%m-%d')
startdate = datetime.datetime.strptime('2007-06-01', '%Y-%m-%d')
data_train['issueDateDT'] = data_train['issueDate'].apply(lambda x: x-startdate).dt.days

#轉化成時間格式
data_test_a['issueDate'] = pd.to_datetime(data_train['issueDate'],format='%Y-%m-%d')
startdate = datetime.datetime.strptime('2007-06-01', '%Y-%m-%d')
data_test_a['issueDateDT'] = data_test_a['issueDate'].apply(lambda x: x-startdate).dt.days

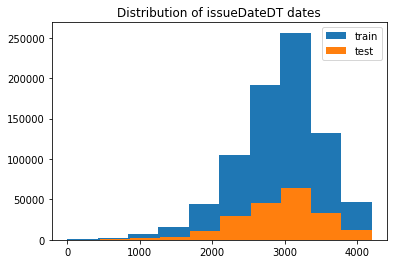
plt.hist(data_train['issueDateDT'], label='train');
plt.hist(data_test_a['issueDateDT'], label='test');
plt.legend();
plt.title('Distribution of issueDateDT dates');
#train 和 test issueDateDT 日期有重疊 所以使用基於時間的分割進行驗證是不明智的

2.3.4 掌握透檢視可以讓我們更好的瞭解資料

#透檢視 索引可以有多個，「columns（列）」是可選的，聚合函數aggfunc最後是被應用到了變數「values」中你所列舉的專案上。
pivot = pd.pivot_table(data_train, index=['grade'], columns=['issueDateDT'], values=['loanAmnt'], aggfunc=np.sum)

pivot

2.3. 用pandas_profiling生成資料包告

import pandas_profiling

pfr = pandas_profiling.ProfileReport(data_train)
pfr.to_file("./example.html")

2.4 總結

資料探索性分析是我們初步瞭解資料，熟悉資料為特徵工程做準備的階段，甚至很多時候EDA階段提取出來的特徵可以直接當作規則來用。可見EDA的重要性，這個階段的主要工作還是藉助於各個簡單的統計量來對資料整體的瞭解，分析各個型別變數相互之間的關係，以及用合適的圖形視覺化出來直觀觀察。希望本節內容能給初學者帶來幫助，更期待各位學習者對其中的不足提出建議。

3.特徵工程

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import datetime
from tqdm import tqdm
from sklearn.preprocessing import LabelEncoder
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
from sklearn.preprocessing import MinMaxScaler
import xgboost as xgb
import lightgbm as lgb
from catboost import CatBoostRegressor
import warnings
from sklearn.model_selection import StratifiedKFold, KFold
from sklearn.metrics import accuracy_score, f1_score, roc_auc_score, log_loss
warnings.filterwarnings('ignore')

data_train =pd.read_csv('../train.csv')
data_test_a = pd.read_csv('../testA.csv')

3.1 特徵預處理

• 資料EDA部分我們已經對資料的大概和某些特徵分佈有了瞭解，資料預處理部分一般我們要處理一些EDA階段分析出來的問題，這裡介紹了資料缺失值的填充，時間格式特徵的轉化處理，某些物件類別特徵的處理。

首先我們查詢出資料中的物件特徵和數值特徵

numerical_fea = list(data_train.select_dtypes(exclude=['object']).columns)
category_fea = list(filter(lambda x: x not in numerical_fea,list(data_train.columns)))
label = 'isDefault'
numerical_fea.remove(label)

在比賽中資料預處理是必不可少的一部分，對於缺失值的填充往往會影響比賽的結果，在比賽中不妨嘗試多種填充然後比較結果選擇結果最優的一種；
比賽資料相比真實場景的資料相對要「乾淨」一些，但是還是會有一定的「髒」資料存在，清洗一些異常值往往會獲得意想不到的效果。

• 把所有缺失值替換為指定的值0

  data_train = data_train.fillna(0)

• 向用缺失值上面的值替換缺失值

  data_train = data_train.fillna(axis=0,method='ffill')

• 縱向用缺失值下面的值替換缺失值,且設定最多隻填充兩個連續的缺失值

  data_train = data_train.fillna(axis=0,method='bfill',limit=2)

#檢視缺失值情況
data_train.isnull().sum()

#按照平均數填充數值型特徵
data_train[numerical_fea] = data_train[numerical_fea].fillna(data_train[numerical_fea].median())
data_test_a[numerical_fea] = data_test_a[numerical_fea].fillna(data_train[numerical_fea].median())
#按照眾數填充類別型特徵
data_train[category_fea] = data_train[category_fea].fillna(data_train[category_fea].mode())
data_test_a[category_fea] = data_test_a[category_fea].fillna(data_train[category_fea].mode())

data_train.isnull().sum()

#檢視類別特徵
category_fea

['grade', 'subGrade', 'employmentLength', 'issueDate', 'earliesCreditLine']

• category_fea：物件型類別特徵需要進行預處理，其中['issueDate']為時間格式特徵。

#轉化成時間格式
for data in [data_train, data_test_a]:
    data['issueDate'] = pd.to_datetime(data['issueDate'],format='%Y-%m-%d')
    startdate = datetime.datetime.strptime('2007-06-01', '%Y-%m-%d')
    #構造時間特徵
    data['issueDateDT'] = data['issueDate'].apply(lambda x: x-startdate).dt.days

data_train['employmentLength'].value_counts(dropna=False).sort_index()

1 year        52489
10+ years    262753
2 years       72358
3 years       64152
4 years       47985
5 years       50102
6 years       37254
7 years       35407
8 years       36192
9 years       30272
< 1 year      64237
NaN           46799
Name: employmentLength, dtype: int64

def employmentLength_to_int(s):
    if pd.isnull(s):
        return s
    else:
        return np.int8(s.split()[0])
for data in [data_train, data_test_a]:
    data['employmentLength'].replace(to_replace='10+ years', value='10 years', inplace=True)
    data['employmentLength'].replace('< 1 year', '0 years', inplace=True)
    data['employmentLength'] = data['employmentLength'].apply(employmentLength_to_int)

data['employmentLength'].value_counts(dropna=False).sort_index()

0.0     15989
1.0     13182
2.0     18207
3.0     16011
4.0     11833
5.0     12543
6.0      9328
7.0      8823
8.0      8976
9.0      7594
10.0    65772
NaN     11742
Name: employmentLength, dtype: int64

• 對earliesCreditLine進行預處理

data_train['earliesCreditLine'].sample(5)

519915    Sep-2002
564368    Dec-1996
768209    May-2004
453092    Nov-1995
763866    Sep-2000
Name: earliesCreditLine, dtype: object

for data in [data_train, data_test_a]:
    data['earliesCreditLine'] = data['earliesCreditLine'].apply(lambda s: int(s[-4:]))

# 部分類別特徵
cate_features = ['grade', 'subGrade', 'employmentTitle', 'homeOwnership', 'verificationStatus', 'purpose', 'postCode', 'regionCode', \
                 'applicationType', 'initialListStatus', 'title', 'policyCode']
for f in cate_features:
    print(f, '型別數：', data[f].nunique())

grade 型別數： 7
subGrade 型別數： 35
employmentTitle 型別數： 79282
homeOwnership 型別數： 6
verificationStatus 型別數： 3
purpose 型別數： 14
postCode 型別數： 889
regionCode 型別數： 51
applicationType 型別數： 2
initialListStatus 型別數： 2
title 型別數： 12058
policyCode 型別數： 1

像等級這種類別特徵，是有優先順序的可以labelencode或者自對映

for data in [data_train, data_test_a]:
    data['grade'] = data['grade'].map({'A':1,'B':2,'C':3,'D':4,'E':5,'F':6,'G':7})

# 型別數在2之上，又不是高維稀疏的,且純分類特徵
for data in [data_train, data_test_a]:
    data = pd.get_dummies(data, columns=['subGrade', 'homeOwnership', 'verificationStatus', 'purpose', 'regionCode'], drop_first=True)

3.2 異常值處理

• 當你發現異常值後，一定要先分清是什麼原因導致的異常值，然後再考慮如何處理。首先，如果這一異常值並不代表一種規律性的，而是極其偶然的現象，或者說你並不想研究這種偶然的現象，這時可以將其刪除。其次，如果異常值存在且代表了一種真實存在的現象，那就不能隨便刪除。在現有的欺詐場景中很多時候欺詐資料本身相對於正常資料勒說就是異常的，我們要把這些異常點納入，重新擬合模型，研究其規律。能用監督的用監督模型，不能用的還可以考慮用異常檢測的演演算法來做。
• 注意test的資料不能刪。

3.2.1 檢測異常的方法一：均方差

在統計學中，如果一個資料分佈近似正態，那麼大約 68% 的資料值會在均值的一個標準差範圍內，大約 95% 會在兩個標準差範圍內，大約 99.7% 會在三個標準差範圍內。

def find_outliers_by_3segama(data,fea):
    data_std = np.std(data[fea])
    data_mean = np.mean(data[fea])
    outliers_cut_off = data_std * 3
    lower_rule = data_mean - outliers_cut_off
    upper_rule = data_mean + outliers_cut_off
    data[fea+'_outliers'] = data[fea].apply(lambda x:str('異常值') if x > upper_rule or x < lower_rule else '正常值')
    return data

• 得到特徵的異常值後可以進一步分析變數異常值和目標變數的關係

data_train = data_train.copy()
for fea in numerical_fea:
    data_train = find_outliers_by_3segama(data_train,fea)
    print(data_train[fea+'_outliers'].value_counts())
    print(data_train.groupby(fea+'_outliers')['isDefault'].sum())
    print('*'*10)

• 例如可以看到異常值在兩個變數上的分佈幾乎複合整體的分佈，如果異常值都屬於為1的使用者資料裡面代表什麼呢？

#刪除異常值
for fea in numerical_fea:
    data_train = data_train[data_train[fea+'_outliers']=='正常值']
    data_train = data_train.reset_index(drop=True) 

3.2.1檢測異常的方法二：箱型圖

• 總結一句話：四分位數會將資料分為三個點和四個區間，IQR = Q3 -Q1，下觸鬚=Q1 − 1.5x IQR，上觸鬚=Q3 + 1.5x IQR；

3.3 資料分桶

• 特徵分箱的目的：

  • 從模型效果上來看，特徵分箱主要是為了降低變數的複雜性，減少變數噪音對模型的影響，提高自變數和因變數的相關度。從而使模型更加穩定。

• 資料分桶的物件：

  • 將連續變數離散化
  • 將多狀態的離散變數合併成少狀態

• 分箱的原因：

  • 資料的特徵內的值跨度可能比較大，對有監督和無監督中如k-均值聚類它使用歐氏距離作為相似度函數來測量資料點之間的相似度。都會造成大吃小的影響，其中一種解決方法是對計數值進行區間量化即資料分桶也叫做資料分箱，然後使用量化後的結果。

• 分箱的優點：

  • 處理缺失值：當資料來源可能存在缺失值，此時可以把null單獨作為一個分箱。
  • 處理異常值：當資料中存在離群點時，可以把其通過分箱離散化處理，從而提高變數的魯棒性（抗干擾能力）。例如，age若出現200這種異常值，可分入「age > 60」這個分箱裡，排除影響。
  • 業務解釋性：我們習慣於線性判斷變數的作用，當x越來越大，y就越來越大。但實際x與y之間經常存在著非線性關係，此時可經過WOE變換。

• 特別要注意一下分箱的基本原則：

  • （1）最小分箱佔比不低於5%
  • （2）箱內不能全部是好客戶
  • （3）連續箱單調

1. 固定寬度分箱

當數值橫跨多個數量級時，最好按照 10 的冪（或任何常數的冪）來進行分組：0_9、1099、100_999、10009999，等等。固定寬度分箱非常容易計算，但如果計數值中有比較大的缺口，就會產生很多沒有任何資料的空箱子。

#通過除法對映到間隔均勻的分箱中，每個分箱的取值範圍都是loanAmnt/1000
data['loanAmnt_bin1'] = np.floor_divide(data['loanAmnt'], 1000)

##通過對數函數對映到指數寬度分箱
data['loanAmnt_bin2'] = np.floor(np.log10(data['loanAmnt']))

2. 分位數分箱

data['loanAmnt_bin3'] = pd.qcut(data['loanAmnt'], 10, labels=False)

3. 卡方分箱及其他分箱方法的嘗試

• 這一部分屬於進階部分，學有餘力的同學可以自行搜尋嘗試。

3.4 特徵互動

• 互動特徵的構造非常簡單，使用起來卻代價不菲。如果線性模型中包含有互動特徵對，那它的訓練時間和評分時間就會從 O(n) 增加到 O(n2)，其中 n 是單一特徵的數量。

for col in ['grade', 'subGrade']: 
    temp_dict = data_train.groupby([col])['isDefault'].agg(['mean']).reset_index().rename(columns={'mean': col + '_target_mean'})
    temp_dict.index = temp_dict[col].values
    temp_dict = temp_dict[col + '_target_mean'].to_dict()

    data_train[col + '_target_mean'] = data_train[col].map(temp_dict)
    data_test_a[col + '_target_mean'] = data_test_a[col].map(temp_dict)

# 其他衍生變數 mean 和 std
for df in [data_train, data_test_a]:
    for item in ['n0','n1','n2','n2.1','n4','n5','n6','n7','n8','n9','n10','n11','n12','n13','n14']:
        df['grade_to_mean_' + item] = df['grade'] / df.groupby([item])['grade'].transform('mean')
        df['grade_to_std_' + item] = df['grade'] / df.groupby([item])['grade'].transform('std')

這裡給出一些特徵互動的思路，但特徵和特徵間的互動衍生出新的特徵還遠遠不止於此，拋磚引玉，希望大家多多探索。請學習者嘗試其他的特徵互動方法。

3.5 特徵編碼

3.5.1labelEncode 直接放入樹模型中

#label-encode:subGrade,postCode,title
#高維類別特徵需要進行轉換
for col in tqdm(['employmentTitle', 'postCode', 'title','subGrade']):
    le = LabelEncoder()
    le.fit(list(data_train[col].astype(str).values) + list(data_test_a[col].astype(str).values))
    data_train[col] = le.transform(list(data_train[col].astype(str).values))
    data_test_a[col] = le.transform(list(data_test_a[col].astype(str).values))
print('Label Encoding 完成')

100%|██████████| 4/4 [00:08<00:00,  2.04s/it]

Label Encoding 完成

3.5.2邏輯迴歸等模型要單獨增加的特徵工程

• 對特徵做歸一化，去除相關性高的特徵
• 歸一化目的是讓訓練過程更好更快的收斂，避免特徵大吃小的問題
• 去除相關性是增加模型的可解釋性，加快預測過程。

# 舉例歸一化過程
#虛擬碼
for fea in [要歸一化的特徵列表]：
    data[fea] = ((data[fea] - np.min(data[fea])) / (np.max(data[fea]) - np.min(data[fea])))

3.6 特徵選擇

• 特徵選擇技術可以精簡掉無用的特徵，以降低最終模型的複雜性，它的最終目的是得到一個簡約模型，在不降低預測準確率或對預測準確率影響不大的情況下提高計算速度。特徵選擇不是為了減少訓練時間（實際上，一些技術會增加總體訓練時間），而是為了減少模型評分時間。

特徵選擇的方法：

• 1 Filter
  • 方差選擇法
  • 相關係數法（pearson 相關係數）
  • 卡方檢驗
  • 互資訊法
• 2 Wrapper （RFE）
  • 遞迴特徵消除法
• 3 Embedded
  • 基於懲罰項的特徵選擇法
  • 基於樹模型的特徵選擇

3.6.1Filter（方差選擇法、相關係數法）

• 基於特徵間的關係進行篩選

方差選擇法

• 方差選擇法中，先要計算各個特徵的方差，然後根據設定的閾值，選擇方差大於閾值的特徵

from sklearn.feature_selection import VarianceThreshold
#其中引數threshold為方差的閾值
VarianceThreshold(threshold=3).fit_transform(train,target_train)

相關係數法

• Pearson 相關係數
  皮爾森相關係數是一種最簡單的，可以幫助理解特徵和響應變數之間關係的方法，該方法衡量的是變數之間的線性相關性。
  結果的取值區間為 [-1，1] ， -1 表示完全的負相關， +1表示完全的正相關，0 表示沒有線性相關。

from sklearn.feature_selection import SelectKBest
from scipy.stats import pearsonr
#選擇K個最好的特徵，返回選擇特徵後的資料
#第一個引數為計算評估特徵是否好的函數，該函數輸入特徵矩陣和目標向量，
#輸出二元組（評分，P值）的陣列，陣列第i項為第i個特徵的評分和P值。在此定義為計算相關係數
#引數k為選擇的特徵個數

SelectKBest(k=5).fit_transform(train,target_train)

卡方檢驗

• 經典的卡方檢驗是用於檢驗自變數對因變數的相關性。 假設自變數有N種取值，因變數有M種取值，考慮自變數等於i且因變數等於j的樣本頻數的觀察值與期望的差距。 其統計量如下： χ2=∑(A−T)2T，其中A為實際值，T為理論值
• (注：卡方只能運用在正定矩陣上，否則會報錯Input X must be non-negative)

from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
#引數k為選擇的特徵個數

SelectKBest(chi2, k=5).fit_transform(train,target_train)

互資訊法

• 經典的互資訊也是評價自變數對因變數的相關性的。 在feature_selection庫的SelectKBest類結合最大資訊系數法可以用於選擇特徵，相關程式碼如下：

from sklearn.feature_selection import SelectKBest
from minepy import MINE
#由於MINE的設計不是函數式的，定義mic方法將其為函數式的，
#返回一個二元組，二元組的第2項設定成固定的P值0.5
def mic(x, y):
    m = MINE()
    m.compute_score(x, y)
    return (m.mic(), 0.5)
#引數k為選擇的特徵個數
SelectKBest(lambda X, Y: array(map(lambda x:mic(x, Y), X.T)).T, k=2).fit_transform(train,target_train)

3.6.2Wrapper （遞迴特徵法）

• 遞迴特徵消除法 遞迴消除特徵法使用一個基模型來進行多輪訓練，每輪訓練後，消除若干權值係數的特徵，再基於新的特徵集進行下一輪訓練。 在feature_selection庫的RFE類可以用於選擇特徵，相關程式碼如下（以邏輯迴歸為例）：

from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression
#遞迴特徵消除法，返回特徵選擇後的資料
#引數estimator為基模型
#引數n_features_to_select為選擇的特徵個數

RFE(estimator=LogisticRegression(), n_features_to_select=2).fit_transform(train,target_train)

3.6.3Embedded（ 懲罰項的特徵選擇法、樹模型的特徵選擇）

• 基於懲罰項的特徵選擇法 使用帶懲罰項的基模型，除了篩選出特徵外，同時也進行了降維。 在feature_selection庫的SelectFromModel類結合邏輯迴歸模型可以用於選擇特徵，相關程式碼如下：

from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression
#帶L1懲罰項的邏輯迴歸作為基模型的特徵選擇

SelectFromModel(LogisticRegression(penalty="l1", C=0.1)).fit_transform(train,target_train)

• 基於樹模型的特徵選擇 樹模型中GBDT也可用來作為基模型進行特徵選擇。 在feature_selection庫的SelectFromModel類結合GBDT模型可以用於選擇特徵，相關程式碼如下：

from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import GradientBoostingClassifier
#GBDT作為基模型的特徵選擇
SelectFromModel(GradientBoostingClassifier()).fit_transform(train,target_train)

本資料集中我們刪除非入模特徵後，並對缺失值填充，然後用計算協方差的方式看一下特徵間相關性，然後進行模型訓練

# 刪除不需要的資料
for data in [data_train, data_test_a]:
    data.drop(['issueDate','id'], axis=1,inplace=True)

"縱向用缺失值上面的值替換缺失值"
data_train = data_train.fillna(axis=0,method='ffill')

x_train = data_train.drop(['isDefault','id'], axis=1)
#計算協方差
data_corr = x_train.corrwith(data_train.isDefault) #計算相關性
result = pd.DataFrame(columns=['features', 'corr'])
result['features'] = data_corr.index
result['corr'] = data_corr.values

# 當然也可以直接看圖
data_numeric = data_train[numerical_fea]
correlation = data_numeric.corr()

f , ax = plt.subplots(figsize = (7, 7))
plt.title('Correlation of Numeric Features with Price',y=1,size=16)
sns.heatmap(correlation,square = True,  vmax=0.8)

<matplotlib.axes._subplots.AxesSubplot at 0x12d88ad10>

features = [f for f in data_train.columns if f not in ['id','issueDate','isDefault'] and '_outliers' not in f]
x_train = data_train[features]
x_test = data_test_a[features]
y_train = data_train['isDefault']

def cv_model(clf, train_x, train_y, test_x, clf_name):
    folds = 5
    seed = 2020
    kf = KFold(n_splits=folds, shuffle=True, random_state=seed)

    train = np.zeros(train_x.shape[0])
    test = np.zeros(test_x.shape[0])

    cv_scores = []

    for i, (train_index, valid_index) in enumerate(kf.split(train_x, train_y)):
        print('************************************ {} ************************************'.format(str(i+1)))
        trn_x, trn_y, val_x, val_y = train_x.iloc[train_index], train_y[train_index], train_x.iloc[valid_index], train_y[valid_index]

        if clf_name == "lgb":
            train_matrix = clf.Dataset(trn_x, label=trn_y)
            valid_matrix = clf.Dataset(val_x, label=val_y)

            params = {
                'boosting_type': 'gbdt',
                'objective': 'binary',
                'metric': 'auc',
                'min_child_weight': 5,
                'num_leaves': 2 ** 5,
                'lambda_l2': 10,
                'feature_fraction': 0.8,
                'bagging_fraction': 0.8,
                'bagging_freq': 4,
                'learning_rate': 0.1,
                'seed': 2020,
                'nthread': 28,
                'n_jobs':24,
                'silent': True,
                'verbose': -1,
            }

            model = clf.train(params, train_matrix, 50000, valid_sets=[train_matrix, valid_matrix], verbose_eval=200,early_stopping_rounds=200)
            val_pred = model.predict(val_x, num_iteration=model.best_iteration)
            test_pred = model.predict(test_x, num_iteration=model.best_iteration)
            
            # print(list(sorted(zip(features, model.feature_importance("gain")), key=lambda x: x[1], reverse=True))[:20])
                
        if clf_name == "xgb":
            train_matrix = clf.DMatrix(trn_x , label=trn_y)
            valid_matrix = clf.DMatrix(val_x , label=val_y)
            
            params = {'booster': 'gbtree',
                      'objective': 'binary:logistic',
                      'eval_metric': 'auc',
                      'gamma': 1,
                      'min_child_weight': 1.5,
                      'max_depth': 5,
                      'lambda': 10,
                      'subsample': 0.7,
                      'colsample_bytree': 0.7,
                      'colsample_bylevel': 0.7,
                      'eta': 0.04,
                      'tree_method': 'exact',
                      'seed': 2020,
                      'nthread': 36,
                      "silent": True,
                      }
            
            watchlist = [(train_matrix, 'train'),(valid_matrix, 'eval')]
            
            model = clf.train(params, train_matrix, num_boost_round=50000, evals=watchlist, verbose_eval=200, early_stopping_rounds=200)
            val_pred  = model.predict(valid_matrix, ntree_limit=model.best_ntree_limit)
            test_pred = model.predict(test_x , ntree_limit=model.best_ntree_limit)
                 
        if clf_name == "cat":
            params = {'learning_rate': 0.05, 'depth': 5, 'l2_leaf_reg': 10, 'bootstrap_type': 'Bernoulli',
                      'od_type': 'Iter', 'od_wait': 50, 'random_seed': 11, 'allow_writing_files': False}
            
            model = clf(iterations=20000, **params)
            model.fit(trn_x, trn_y, eval_set=(val_x, val_y),
                      cat_features=[], use_best_model=True, verbose=500)
            
            val_pred  = model.predict(val_x)
            test_pred = model.predict(test_x)
            
        train[valid_index] = val_pred
        test = test_pred / kf.n_splits
        cv_scores.append(roc_auc_score(val_y, val_pred))
        
        print(cv_scores)
        
    print("%s_scotrainre_list:" % clf_name, cv_scores)
    print("%s_score_mean:" % clf_name, np.mean(cv_scores))
    print("%s_score_std:" % clf_name, np.std(cv_scores))
    return train, test

def lgb_model(x_train, y_train, x_test):
    lgb_train, lgb_test = cv_model(lgb, x_train, y_train, x_test, "lgb")
    return lgb_train, lgb_test

def xgb_model(x_train, y_train, x_test):
    xgb_train, xgb_test = cv_model(xgb, x_train, y_train, x_test, "xgb")
    return xgb_train, xgb_test

def cat_model(x_train, y_train, x_test):
    cat_train, cat_test = cv_model(CatBoostRegressor, x_train, y_train, x_test, "cat")

lgb_train, lgb_test = lgb_model(x_train, y_train, x_test)

************************************ 1 ************************************
Training until validation scores don't improve for 200 rounds
[200]	training's auc: 0.749225	valid_1's auc: 0.729679
[400]	training's auc: 0.765075	valid_1's auc: 0.730496
[600]	training's auc: 0.778745	valid_1's auc: 0.730435
Early stopping, best iteration is:
[455]	training's auc: 0.769202	valid_1's auc: 0.730686
[0.7306859913754798]
************************************ 2 ************************************
Training until validation scores don't improve for 200 rounds
[200]	training's auc: 0.749221	valid_1's auc: 0.731315
[400]	training's auc: 0.765117	valid_1's auc: 0.731658
[600]	training's auc: 0.778542	valid_1's auc: 0.731333
Early stopping, best iteration is:
[407]	training's auc: 0.765671	valid_1's auc: 0.73173
[0.7306859913754798, 0.7317304414673989]
************************************ 3 ************************************
Training until validation scores don't improve for 200 rounds
[200]	training's auc: 0.748436	valid_1's auc: 0.732775
[400]	training's auc: 0.764216	valid_1's auc: 0.733173
Early stopping, best iteration is:
[386]	training's auc: 0.763261	valid_1's auc: 0.733261
[0.7306859913754798, 0.7317304414673989, 0.7332610441015461]
************************************ 4 ************************************
Training until validation scores don't improve for 200 rounds
[200]	training's auc: 0.749631	valid_1's auc: 0.728327
[400]	training's auc: 0.765139	valid_1's auc: 0.728845
Early stopping, best iteration is:
[286]	training's auc: 0.756978	valid_1's auc: 0.728976
[0.7306859913754798, 0.7317304414673989, 0.7332610441015461, 0.7289759386807912]
************************************ 5 ************************************
Training until validation scores don't improve for 200 rounds
[200]	training's auc: 0.748414	valid_1's auc: 0.732727
[400]	training's auc: 0.763727	valid_1's auc: 0.733531
[600]	training's auc: 0.777489	valid_1's auc: 0.733566
Early stopping, best iteration is:
[524]	training's auc: 0.772372	valid_1's auc: 0.733772
[0.7306859913754798, 0.7317304414673989, 0.7332610441015461, 0.7289759386807912, 0.7337723979789789]
lgb_scotrainre_list: [0.7306859913754798, 0.7317304414673989, 0.7332610441015461, 0.7289759386807912, 0.7337723979789789]
lgb_score_mean: 0.7316851627208389
lgb_score_std: 0.0017424259863954693

testA_result = pd.read_csv('../testA_result.csv')

roc_auc_score(testA_result['isDefault'].values, lgb_test)

0.7290917729487896

3.8總結

特徵工程是機器學習，甚至是深度學習中最為重要的一部分，在實際應用中往往也是所花費時間最多的一步。各種演演算法書中對特徵工程部分的講解往往少得可憐，因為特徵工程和具體的資料結合的太緊密，很難系統地覆蓋所有場景。本章主要是通過一些常用的方法來做介紹，例如缺失值異常值的處理方法詳細對任何資料集來說都是適用的。但對於分箱等操作本章給出了具體的幾種思路，需要讀者自己探索。在特徵工程中比賽和具體的應用還是有所不同的，在實際的金融風控評分卡製作過程中，由於強調特徵的可解釋性，特徵分箱尤其重要。

專案連結以及碼源

資料探勘專欄

資料探勘實踐（金融風控）：金融風控之貸款違約預測挑戰賽(上篇)

資料探勘實踐（金融風控）：金融風控之貸款違約預測挑戰賽(下篇)