技術文章 » LeetCode 周賽 345（2023/05/14）體驗一題多解的演演算法之美

LeetCode 周賽 345（2023/05/14）體驗一題多解的演演算法之美

2023-05-16 06:01:05

本文已收錄到 AndroidFamily，技術和職場問題，請關注公眾號 [彭旭銳] 提問。

周賽概覽

T1. 找出轉圈遊戲輸家（Easy）

  • 標籤：模擬、計數

T2. 相鄰值的按位元互斥或（Medium）

  • 標籤：模擬、數學、構造

T3. 矩陣中移動的最大次數（Medium）

  • 標籤：圖、BFS、DFS、動態規劃

T4. 統計完全連通分量的數量（Medium）

  • 標籤：圖、BFS、DFS、並查集

T1. 找出轉圈遊戲輸家（Easy）

https://leetcode.cn/problems/find-the-losers-of-the-circular-game/

題解（模擬）

簡單模擬題。

使用標記陣列標記接觸到球的玩家，再根據標記陣列輸出結果：

class Solution {
    fun circularGameLosers(n: Int, k: Int): IntArray {
        val visit = BooleanArray(n)
        var i = 0
        var j = 1
        var cnt = n
        while (!visit[i]) {
            visit[i] = true
            i = (i + j++ * k) % n
            cnt--
        }
        val ret = IntArray(cnt)
        var k = 0
        for (i in visit.indices) {
            if(!visit[i]) ret[k++] = i + 1
        }
        return ret
    }
}

複雜度分析：

  • 時間複雜度：$O(n)$ 每位玩家最多標記一次和檢查一次；
  • 空間複雜度：$O(n)$ 標記陣列空間。

T2. 相鄰值的按位元互斥或（Medium）

https://leetcode.cn/problems/neighboring-bitwise-xor/

預備知識

記 ⊕ 為互斥或運算，互斥或運算滿足以下性質：

  • 基本性質：x ⊕ y = 0
  • 交換律：x ⊕ y = y ⊕ x
  • 結合律：(x ⊕ y) ⊕ z = x ⊕ (y ⊕ z)
  • 自反律：x ⊕ y ⊕ y = x

題解一（模擬）

由於每一位 derived[i] 可以由 original[i] ⊕ original[i + 1] 獲得，我們可以令原始的 original[0] 為 0，再按順序遞推到 original[n]（迴圈陣列），最後再檢查 original[0] 和 original[n] 是否相同。如果不同，說明 derived 陣列是不可構造的。

class Solution {
    fun doesValidArrayExist(derived: IntArray): Boolean {
        var pre = 0
        for ((i,d) in derived.withIndex()) {
            if (d == 1) pre = pre xor 1
        }
        return pre == 0
    }
}

複雜度分析：

  • 時間複雜度：$O(n)$ 其中 n 為 derived 陣列的長度；
  • 空間複雜度：僅使用常數級別空間。

題解二（數學）

繼續挖掘問題的數學性質：

  • 題目要求：$derived[i] = original[i] ⊕ original[i + 1]$
  • 根據自反律（兩邊互斥或 original[i]）：$original[i + 1] = derived[i] ⊕ original[i]$、$original[i + 2] = derived[i + 1] ⊕ original[i + 1]$
  • 根據遞推關係有 $original[n - 1] = derived[n - 2] ⊕ derived[n - 1]… derived[0] ⊕ original[0]$
  • 題目要求：$original[0] ⊕ original[n - 1] = derived[n-1]$
  • 聯合兩式：$original[0] = original[0] ⊕ derived[n-1] ⊕ derived[n - 1]… derived[0] ⊕ original[0]$，即 $0 = derived[n-1] ⊕ derived[n - 1]… derived[0]$

根據結論公式模擬即可：

class Solution {
    fun doesValidArrayExist(derived: IntArray): Boolean {
        // return derived.fold(0) {acc, e -> acc xor e} == 0
        return derived.reduce {acc, e -> acc xor e} == 0
    }
}

複雜度分析：

  • 時間複雜度：$O(n)$ 其中 n 為 derived 陣列的長度；
  • 空間複雜度：僅使用常數級別空間。

T3. 矩陣中移動的最大次數（Medium）

https://leetcode.cn/problems/maximum-number-of-moves-in-a-grid/

題目描述

給你一個下標從 0 開始、大小為 m x n 的矩陣 grid ，矩陣由若干 正 整陣列成。

你可以從矩陣第一列中的 任一 單元格出發，按以下方式遍歷 grid ：

  • 從單元格 (row, col) 可以移動到 (row - 1, col + 1)、(row, col + 1) 和 (row + 1, col + 1) 三個單元格中任一滿足值 嚴格 大於當前單元格的單元格。

返回你在矩陣中能夠 移動 的 最大 次數。

範例 1：

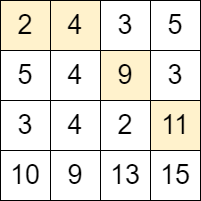
輸入：grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
輸出：3
解釋：可以從單元格 (0, 0) 開始並且按下面的路徑移動：
- (0, 0) -> (0, 1).
- (0, 1) -> (1, 2).
- (1, 2) -> (2, 3).
可以證明這是能夠移動的最大次數。

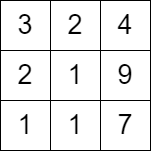
範例 2：

輸入：grid = [[3,2,4],[2,1,9],[1,1,7]]
輸出：0
解釋：從第一列的任一單元格開始都無法移動。

提示：

  • m == grid.length
  • n == grid[i].length
  • 2 <= m, n <= 1000
  • 4 <= m * n <= 105
  • 1 <= grid[i][j] <= 106

問題結構化

1、概括問題目標

計算可移動的最大次數，也可以理解為可存取距離 - 1。

2、分析問題要件

在每次移動操作中，可以移動到右邊一列的最近三行位置（i-1, i, j+1）且要求數位嚴格大於當前位置。

3、提高抽象程度

  • 子問題：我們發現每次移動後，可移動次數就是在新位置可移動次數 + 1，這是一個與原問題相似但規模更小的子問題；
  • 是否為決策問題？由於每次移動最多有三個位置選擇，因此這是決策問題。

4、具體化解決手段

  • 手段 1（記憶化遞迴）：定義 dfs(i, j) 表示從 grid[i][j] 開始的最大移動次數，那麼有 dfs(i, j)= mas{dfs(i-1, j+1), dfs(i, j+1), dfs(i+1, j+1)}；
  • 手段 2（遞推）：在記憶化遞迴中我們是在「歸」的過程中合併子問題的解，由於遞迴的方向是驗證矩陣從上到下，從左到右的，我們可以消除「遞」的過程而只保留「歸」的過程，將遞迴轉換為遞推；
  • 手段 3（BFS）：由於可移動次數取決於最多可以移動到的列號，我們可以用 BFS / DFS 搜尋最遠可以存取的列號。

題解一（記憶化遞迴）

根據「手段 1」模擬即可：

  • 遞迴函數：dfs(i, j)= mas
  • 起始狀態：dfs(i, 0)
  • 邊界條件：dfs(i, j) = 0
class Solution {

    val directions = arrayOf(intArrayOf(-1, 1), intArrayOf(0, 1), intArrayOf(1, 1)) // 右上、右、右下

    private val memo = HashMap<Int, Int>()
    private val U = 1001

    fun maxMoves(grid: Array<IntArray>): Int {
        var ret = 0
        for (i in 0 until grid.size) {
            ret = Math.max(ret, dfs(grid, i, 0))
        }
        return ret - 1
    }

    private fun dfs(grid: Array<IntArray>, i: Int, j: Int): Int {
        val n = grid.size
        val m = grid[0].size
        val key = i * U + j
        if (memo.contains(key)) return memo[key]!!
        // 列舉選項
        var maxChoice = 0
        for (direction in directions) {
            val newI = i + direction[0]
            val newJ = j + direction[1]
            if (newI < 0 || newI >= n || newJ < 0 || newJ >= m || grid[i][j] >= grid[newI][newJ]) continue
            maxChoice = Math.max(maxChoice, dfs(grid, newI, newJ))
        }
        memo[key] = maxChoice + 1
        return maxChoice + 1
    }
}

複雜度分析：

  • 時間複雜度：$O(nm)$ 總共有 nm 個子問題，每個子問題列舉 3 個選項時間複雜度是 O(1)；
  • 空間複雜度：$O(nm)$ 備忘錄空間。

題解二（遞推）

消除「遞」的過程而只保留「歸」的過程，將遞迴轉換為遞推：

class Solution {
    fun maxMoves(grid: Array<IntArray>): Int {
        val n = grid.size
        val m = grid[0].size
        val step = Array(n) { IntArray(m) }
        for (i in 0 until n) step[i][0] = 1
        var ret = 0
        // 按列遍歷
        for(j in 1 until m) {
            for(i in 0 until n) {
                for(k in Math.max(0, i - 1) .. Math.min(n - 1,i + 1)) {
                    if (step[k][j - 1] > 0 && grid[i][j] > grid[k][j - 1]) step[i][j] = Math.max(step[i][j], step[k][j - 1] + 1)
                }
                ret = Math.max(ret, step[i][j])
            }
        }
        return Math.max(ret - 1, 0)
    }
}

另外，我們也可以用捲動陣列優化空間：

class Solution {
    fun maxMoves(grid: Array<IntArray>): Int {
        val n = grid.size
        val m = grid[0].size
        var step = IntArray(n) { 1 }
        var ret = 0
        // 按列遍歷
        for(j in 1 until m) {
            val newStep = IntArray(n) { 0 } // 不能直接在 step 陣列上修改
            for(i in 0 until n) {
                for(k in Math.max(0, i - 1) .. Math.min(n - 1,i + 1)) {
                    if (step[k] > 0 && grid[i][j] > grid[k][j - 1]) newStep[i] = Math.max(newStep[i], step[k] + 1)
                }
                ret = Math.max(ret, newStep[i])
            }
            step = newStep
        }
        return Math.max(ret - 1, 0)
    }
}

複雜度分析：

  • 時間複雜度：$O(nm)$
  • 空間複雜度：$O(n)$

題解三（BFS）

按照廣度優先搜尋，使用佇列維護可以存取的節點，再使用該節點探測下一層可到達的位置併入隊。

class Solution {
    fun maxMoves(grid: Array<IntArray>): Int {
        val n = grid.size
        val m = grid[0].size
        // 行號
        var queue = LinkedList<Int>()
        for (i in 0 until n) {
            queue.offer(i)
        }
        // 存取標記
        val visit = IntArray(n) { -1 }
        // 列舉列
        for (j in 0 until m - 1) {
            val newQueue = LinkedList<Int>() // 不能直接在 step 陣列上修改
            for (i in queue) {
                for (k in Math.max(0, i - 1)..Math.min(n - 1, i + 1)) {
                    if (visit[k] < j && grid[k][j + 1] > grid[i][j]) {
                        newQueue.offer(k)
                        visit[k] = j
                    }
                }
            }
            queue = newQueue
            if (queue.isEmpty()) return j
        }
        return m - 1
    }
}

複雜度分析：

  • 時間複雜度：$O(nm)$
  • 空間複雜度：$O(n)$

相似問題：

T4. 統計完全連通分量的數量（Medium）

https://leetcode.cn/problems/count-the-number-of-complete-components/

問題描述

給你一個整數 n 。現有一個包含 n 個頂點的 無向 圖，頂點按從 0 到 n - 1 編號。給你一個二維整數陣列 edges 其中 edges[i] = [ai, bi] 表示頂點 ai 和 bi 之間存在一條 無向 邊。

返回圖中 完全連通分量 的數量。

如果在子圖中任意兩個頂點之間都存在路徑，並且子圖中沒有任何一個頂點與子圖外部的頂點共用邊，則稱其為 連通分量 。

如果連通分量中每對節點之間都存在一條邊，則稱其為 完全連通分量 。

範例 1：

輸入：n = 6, edges = [[0,1],[0,2],[1,2],[3,4]]
輸出：3
解釋：如上圖所示，可以看到此圖所有分量都是完全連通分量。

範例 2：

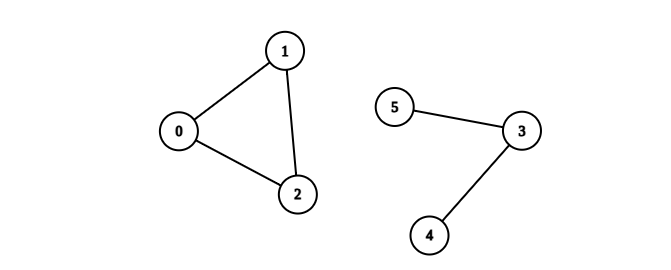
輸入：n = 6, edges = [[0,1],[0,2],[1,2],[3,4],[3,5]]
輸出：1
解釋：包含節點 0、1 和 2 的分量是完全連通分量，因為每對節點之間都存在一條邊。
包含節點 3 、4 和 5 的分量不是完全連通分量，因為節點 4 和 5 之間不存在邊。
因此，在圖中完全連線分量的數量是 1 。

提示：

  • 1 <= n <= 50
  • 0 <= edges.length <= n * (n - 1) / 2
  • edges[i].length == 2
  • 0 <= ai, bi <= n - 1
  • ai != bi
  • 不存在重複的邊

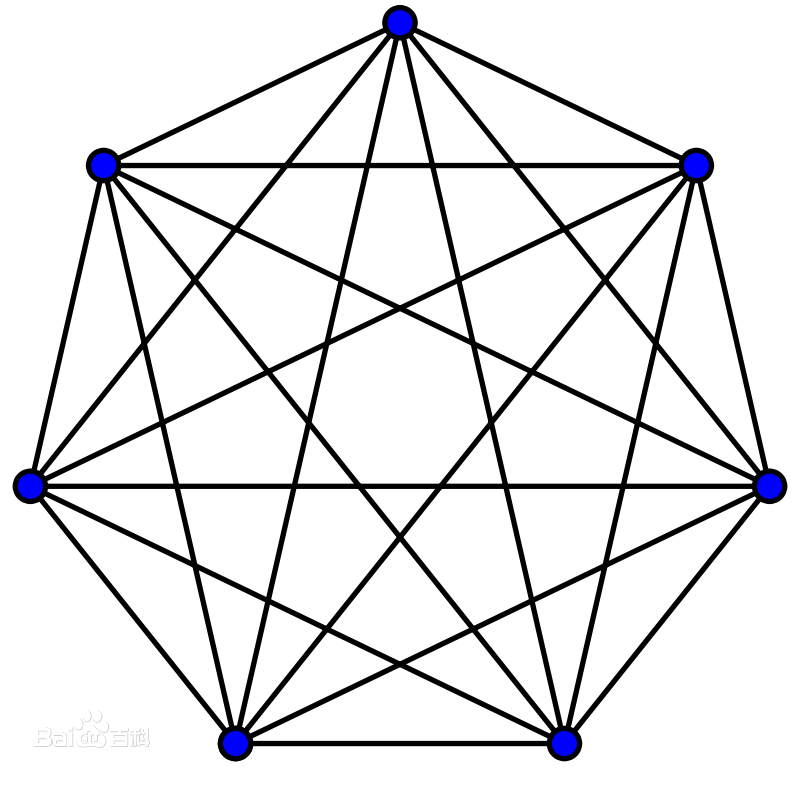
預備知識 - 完全圖

完全圖中每對不同的頂點之間都恰連有一條邊相連，n 個節點的完全圖有 n*(n − 1) / 2 條邊。

問題分析

這道題是比較直接的島嶼 / 連通分量問題，我們直接跑 DFS / BFS / 並查集，計算每個連通分量的節點數和邊數是否平衡。

如果連通分量是完全圖，那麼節點數 v 和邊數 e 滿足 e == v * (v - 2) / 2

題解一（DFS）

列舉每個節點跑 DFS，統計相同連通分量的節點數 v 和節點數 e，由於在遍歷的時候，同一條邊會在兩個節點上重複統計，所以判斷連通分量是否為完全圖的公式調整為 e == v * (v - 2)。

class Solution {
    fun countCompleteComponents(n: Int, edges: Array<IntArray>): Int {
        // 建圖（鄰接表）
        val graph = Array(n) { mutableListOf<Int>() }
        for (edge in edges) {
            graph[edge[0]].add(edge[1])
            graph[edge[1]].add(edge[0]) // 無向邊
        }
        // 標記陣列
        val visit = BooleanArray(n)
        // 列舉
        var ret = 0
        for (i in 0 until n) {
            if (visit[i]) continue
            val cnt = IntArray(2) // v, e
            dfs(graph, visit, i, cnt)
            if (cnt[1] == cnt[0] * (cnt[0] - 1)) ret++
        }
        return ret
    }

    private fun dfs(graph: Array<out List<Int>>, visit: BooleanArray, i: Int, cnt: IntArray) {
        visit[i] = true
        cnt[0] += 1 // 增加節點
        cnt[1] += graph[i].size // 增加邊（會統計兩次）
        for (to in graph[i]) {
            if (!visit[to]) dfs(graph, visit, to, cnt)
        }
    }
}

複雜度分析：

  • 時間複雜度：$O(n + m)$ 其中 n 為節點數，m 為 edges 的長度；
  • 空間複雜度：圖空間 $O(m)$，標記陣列空間 $O(n)$。

題解二（BFS）

附贈一份 BFS 程式碼：

class Solution {
    fun countCompleteComponents(n: Int, edges: Array<IntArray>): Int {
        // 建圖（鄰接表）
        val graph = Array(n) { mutableListOf<Int>() }
        for (edge in edges) {
            graph[edge[0]].add(edge[1])
            graph[edge[1]].add(edge[0]) // 無向邊
        }
        // 標記陣列
        val visit = BooleanArray(n)
        // 列舉
        var ret = 0
        for (i in 0 until n) {
            if (visit[i]) continue
            var v = 0
            var e = 0
            // BFS
            var queue = LinkedList<Int>()
            queue.offer(i)
            visit[i] = true
            while (!queue.isEmpty()) {
                val temp = queue
                queue = LinkedList<Int>()
                for (j in temp) {
                    v += 1 // 增加節點
                    e += graph[j].size // 增加邊（會統計兩次）
                    for (to in graph[j]) {
                        if (!visit[to]) {
                            queue.offer(to)
                            visit[to] = true
                        }
                    }
                }
            }
            if (e == v * (v - 1)) ret++
        }
        return ret
    }
}

複雜度分析：

  • 時間複雜度：$O(n + m)$ 其中 n 為節點數，m 為 edges 的長度；
  • 空間複雜度：圖空間、標記陣列空間和佇列空間。

題解三（並查集）

附贈一份並查集程式碼：

class Solution {

    fun countCompleteComponents(n: Int, edges: Array<IntArray>): Int {
        val uf = UnionFind(n)
        for (edge in edges) {
            uf.union(edge[0], edge[1])
        }
        return uf.count()
    }

    private class UnionFind(n: Int) {
        private val parent = IntArray(n) { it }
        private val rank = IntArray(n)
        private val e = IntArray(n)
        private val v = IntArray(n) { 1 }

        fun find(x: Int): Int {
            // 路徑壓縮
            var a = x
            while (parent[a] != a) {
                parent[a] = parent[parent[a]]
                a = parent[a]
            }
            return a
        }

        fun union(x: Int, y: Int) {
            val rootX = find(x)
            val rootY = find(y)
            if (rootX == rootY) {
                e[rootX]++
            } else {
                // 按秩合併
                if (rank[rootX] < rank[rootY]) {
                    parent[rootX] = rootY
                    e[rootY] += e[rootX] + 1 // 增加邊
                    v[rootY] += v[rootX] // 增加節點
                } else if (rank[rootY] > rank[rootX]) {
                    parent[rootY] = rootX
                    e[rootX] += e[rootY] + 1
                    v[rootX] += v[rootY]
                } else {
                    parent[rootY] = rootX
                    e[rootX] += e[rootY] + 1
                    v[rootX] += v[rootY]
                    rank[rootX]++
                }
            }
        }

        // 統計連通分量
        fun count(): Int {
            return parent.indices.count { parent[it] == it && v[it] * (v[it] - 1) / 2 == e[it] }
        }
    }
}

複雜度分析：

  • 時間複雜度：$O(n + am)$ 其中 n 為節點數，m 為 edges 的長度，其中 $a$ 為反阿克曼函數。
  • 空間複雜度：$O(n)$ 並查集空間。

往期回顧