SICP:元迴圈求值器(Python實現)
求值器完整實現程式碼我已經上傳到了GitHub倉庫:TinySCM,感興趣的童鞋可以前往檢視。這裡順便強烈推薦UC Berkeley的同名課程CS 61A。
在這個層次結構的最底層是物件語言。物件語言只涉及特定的域,而不涉及物件語言本身(比如它們的文法規則,或其中的其體句子)。如要涉及它們,則要有一種元語言。對於語言的兩個層次這一經驗,所有學習外國語的人都是很熟悉的。然後,就要有一種元元語言來討論元語言,以此類推。
——侯世達《哥德爾、埃舍爾、巴赫:集異璧之大成》
緒論
到目前為止,我們探討的都是通過過程抽象、資料抽象以及模組化等手段來控制系統的複雜性。為了闡釋這些技術,我們一直使用的是同一種程式語言。然而,隨著我們所面對的問題更復雜,我們必須經常轉向新的語言,以便能夠有效地表述自己的想法。實際上,建立新語言是工程設計中控制複雜性的一種威力強大的工作策略,我們常常能通過採用一種新語言而處理複雜問題的能力。
元語言抽象就是建立新的語言。它在工程設計的所有分支中都扮演著重要的角色,在計算機程式設計領域更是特別重要。因為這個領域中,我們不僅可以設計新的語言,還可以通過構造求值器的方式實現這些語言。對某個程式設計語言的求值器(或者直譯器)也是一個過程,在應用於這個語言的一個表示式時,它能夠執行求值這個表示式所要求的動作。
把這一點看做是程式設計語言中最基本的思想一點也不過分:
求值器決定了一個程式設計語言中各種表示式的意義,而它本身也不過就是另一個程式。
事實上,我們幾乎可以把任何程式看做是某個語言的求值器。比如在符號代數中,一個多項式系統包含著多項式的算數規則以及底層的實現,一個符號求導系統亦包含著函數求導的規則以及底層的實現(參見我之前的部落格《SICP:符號求導、集合表示和Huffman樹(Python實現)》)。從這樣一種觀點看,處理大規模計算機系統的技術,與構造新的程式設計語言的技術有緊密的聯絡,而電腦科學中一個重要的思想就是如何去構造適當的描述語言。
接下來我們將要討論如何關於在一些語言的基礎上構造新的語言。在這篇部落格里,我們將用Python語言去構造一個Scheme語言的求值器。事實上求值器的實現語言無關緊要,我們也可以用Scheme語言去構造Scheme語言的求值器。用於被求值語言同樣的語言寫出來的求值器被稱為元迴圈(metacircular)。
從根本上說,元迴圈求值器也就是我們在部落格《SICP:賦值和區域性狀態(Python實現)》中所描述求值的環境模型的一個實現形式。回憶一下,該模型包括兩個部分:
- 在求值一個組合式(combinations)(非特殊形式的複合表示式)時,首先求值其中的子表示式(包括運運算元和運算物件),然後將運運算元的值(即一個過程物件)應用於運算物件的值。
- 在將一個複合過程物件應用於一集實參時,我們將在一個新環境裡求值這個過程的體。構造這一新環境的方式是用一個幀來擴充該過程物件原來的環境,幀中包含的是這個過程的形參與所應用的實參之間的繫結。
這兩條規則描述了求值過程的核心部分,也就是它的基本回圈。在這一回圈中,表示式在環境中的求值被規約到過程對實參的應用,而這種應用又被規約到新的表示式在新的環境中的求值。如此下去,直至我們下降到符號(其值可以在環境中找到)或基本過程(它們可以直接應用)。 如下圖所示:
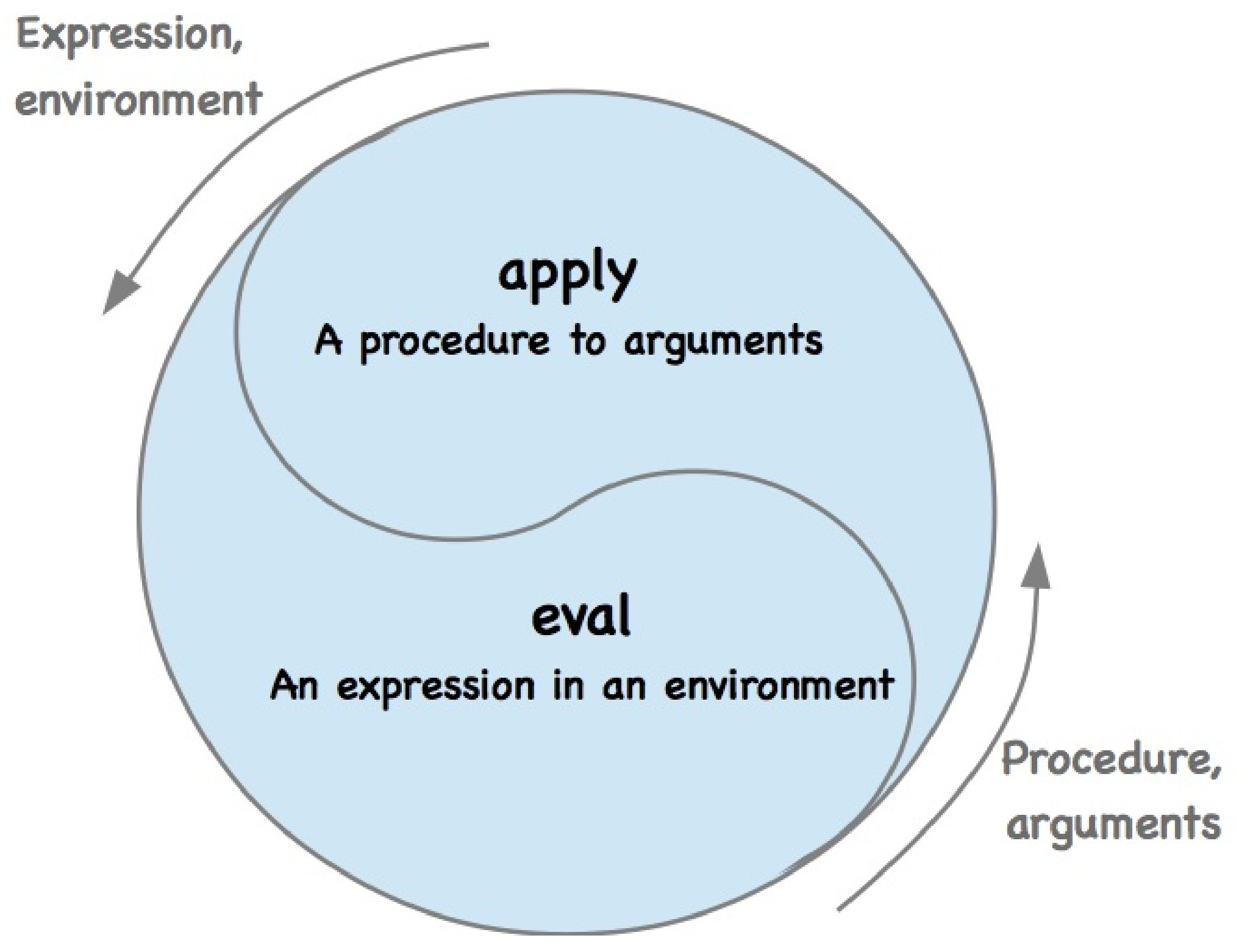
這一求值迴圈實際體現為求值器裡的兩個關鍵函數scheme_eval()和scheme_apply()的相互作用,我們在4.1.1節將描述他們。
求值器的實現依賴於一些定義了被求值表示式的 語法(syntax) (也即被求值表示式是以何種資料結構來表示的)的過程。我們仍將採用自頂向下的資料抽象技術,設法使求值器獨立於語言的具體表示。例如,對於賦值表示式(set! <var> <val>),我們用抽象的選取函數assignment_variable()和assignment_value()去存取賦值中相應的部分(不過這裡需要注意,為了方便後面的型別分派操作,我們仍然假設可以用first_expr()和rest_exprs()分別去存取表示式的首元素和其餘元素,算是對抽象性的一個小小的擊穿吧)。表示式的具體表示將在4.1.2節裡描述。在4.1.3裡還會描述一些過程和環境的表示形式,如Environment類、LambdaProcedure類的定義及其對應的一些方法。
4.1.1 求值器的核心
求值過程可以描述為兩個函數scheme_eval()和scheme_apply()之間的相互作用(interplay)。
eval
scheme_eval()的引數是一個表示式和一個環境。scheme_eval()對錶示式進行分類以此展開後續的求值工作。正如我們上面所說,我們採用選取函數first_expr()和rest_exprs()分別去存取表示式的首元素和其餘元素,並根據表示式的首元素(也即其標籤)來完成表示式型別的判定。表示式的型別可做如下分類:
基本表示式:
- 對於自求值表示式,例如數和字串等(其實也就是我們常說的字面值,literals),
scheme_eval()直接返回這個表示式本身。 - 對於變數,
scheme_eval()必須在環境中查詢變數的值。
特殊形式(special forms):
- 這裡的特殊形式包括
if表示式、變數的賦值/定義、引號(')表示式、lambda表示式等、我們的處理方式是將其分派給不同的名為eval_×××()的求值函數處理。如if表示式就分派給eval_if()函數來處理。
組合式(combinations):
- 這裡的組合式也即過程的應用(application)。對於一個過程應用,
scheme_eval()必須先遞迴地求值組合式的運運算元部分和運算物件部分。而後將這樣得到的過程物件和引數送給scheme_apply(),由它去處理實際的過程應用。注意,如果運運算元部分是宏(Macro),則不需要事先對其進行求值就直接將其應用,待應用完畢之後再進行求值。
下面是scheme_eval()的定義:
@primitive("eval", use_env=True)
def scheme_eval(expr, env, _=None):
# Evaluate self-evaluating expressions
if is_self_evaluating(expr):
return expr
# Evaluate variables
elif is_scheme_variable(expr):
return env.lookup_variable_value(expr)
# All valid non-atomic expressions are lists (combinations)
if not is_scheme_pair(expr):
raise SchemeError(
"Unknown expression type: {0}".format(repl_str(expr)))
first, rest = first_expr(expr), rest_exprs(expr)
# Evaluate special forms
if is_scheme_symbol(first) and first in SPECIAL_FORMS:
return SPECIAL_FORMS[first](rest, env)
# Evaluate an application
else:
operator = scheme_eval(first, env)
# Check if the operator is a macro
if isinstance(operator, MacroProcedure):
return scheme_eval(complete_apply(operator, rest, env), env)
operands = rest.map(lambda x: scheme_eval(x, env))
return scheme_apply(operator, operands, env)
@primitive("eval", use_env=True)表示將其加入Scheme的基本過程中,過程名為eval。這裡的特殊形式的型別分派採用了資料導向的方式(這種做法可以使使用者更容易增加scheme_eval()能分辨的表示式型別,而又不必修改scheme_eval()的定義本身)。所有的SPECIAL_FORMS及其所分派的求值函數如下所示:
SPECIAL_FORMS = {
# Conditionals
"if": eval_if,
"cond": eval_cond,
"and": eval_and,
"or": eval_or,
# Sequencing
"begin": eval_begin,
"let": eval_let,
# Assignments
"set!": eval_assignment,
# Definitions
"define": eval_definition,
# Lambda expressions
"lambda": eval_lambda,
# Quoting
"quote": eval_quote,
"unquote": eval_unquote,
"quasiquote": eval_quasiquote,
# Dynamic scoping
"dlambda": eval_dlambda_form,
# Macro
"define-macro": eval_macro_definition,
# Stream
"delay": eval_delay,
"cons-stream": eval_cons_stream
}
注意這裡的dlambda特殊形式定義的是採用動態作用域的過程,是原Scheme標準中沒有的。
apply
scheme_apply()有兩個引數,一個是過程,一個是該過程去應用的實參表。scheme_apply()將過程分為兩類:基本過程(求值器內建)和複合過程(通過define或lambda/dlambda特殊形式來定義)。對於基本過程,直接呼叫該過程物件的apply()方法去應用實參,對於複合過程,則在新建環境後(該環境包含了形參繫結到實參的新幀),順序地求值組成該過程體的那些表示式。下面是scheme_apply()的定義:
@primitive("apply", use_env=True)
def scheme_apply(procedure, arguments, env):
validate_procedure(procedure)
if is_primitive_procedure(procedure):
return procedure.apply(arguments, env)
elif is_compound_procedure(procedure):
new_env = procedure.make_call_frame(arguments, env)
# Note that `tail` is set to True when `eval_sequence()` is called here
return eval_sequence(procedure.body, new_env, tail=True)
else:
raise SchemeError(
"Unknown procedure type: {0}".format(repl_str(procedure)))
條件
eval_if()先在給定的環境中求值if表示式的謂詞(predicate)部分,如果得到的結果為真,eval_if()就去求值這個if的推論(consequent)部分,否則就求值其替代(alternative)部分。其中需要注意,對於if語句是肯定有推論部分的,但是我們後面會將cond語句的求值規約到對if語句的求值,因cond語句推論可能為空,故此處需要做出判斷——若推論為空,則返回謂詞的求值結果,否則照常對推論求值。此外,如果if語句沒有替代部分,則返回False。
def eval_if(expr, env, tail=True):
validate_form(expr, min=2, max=3)
if_pred = if_predicate(expr)
if_predicate_val = scheme_eval(if_pred, env)
# All values in Scheme are true except `false` object,
# that is why we need `is_scheme_true()`
if is_scheme_true(if_predicate_val):
# Note that for `if` caluse , it muse have consequnet,
# so `if_consequent` can not be None (although it can be `nil`).
# But for `cond` clause, `if_consequent` can be None.
if_conseq = if_consequent(expr)
if if_conseq is None:
return if_predicate_val
else:
return scheme_eval(if_conseq, env, tail=tail)
# Turn to alternative
elif len(expr) == 3:
return scheme_eval(if_alternative(expr), env, tail=tail)
# If there is no alternative, return False
else:
return False
從eval_if()對is_scheme_true()的使用中,我們可以看到被實現語言(Scheme)和實現所用的語言(Python)之間的聯絡。if_predicate()在被實現的語言裡求值,產出這一語言裡的一個值,而直譯器的謂詞is_scheme_true()實際上會將該值翻譯為可由實現所用語言的if檢測的值。這裡因為在Scheme中,除了False之外的物件都應被判斷為真,故我們實際上需要用Python將is_scheme_true()實現如下:
def is_scheme_true(val):
return val is not False
注意這裡如果物件為真則返回該物件本身,而不是直接返回True。
至於cond表示式,可以做為派生表示式(derived expressions)由if表示式實現出來,而不必直接去實現。
def eval_cond(expr, env, tail=True):
return scheme_eval(cond_to_if(expr), env, tail)
最後,我們還需要實現and和or這兩個布林表示式:
def eval_and(exprs, env, tail=True):
# If there is no expression to be evaluated, return True
if exprs is nil:
return True
# If the last expression is reached (indicating that the values of the
# previous expressions are all true), then the evaluation result is
# returned directly
elif rest_exprs(exprs) is nil:
return scheme_eval(first_expr(exprs), env, tail=tail)
value = scheme_eval(first_expr(exprs), env)
# If an expression evaluates to False, return False,
# and the remaining expressions are not evaluated
if is_scheme_false(value):
return False
else:
# If an expression evaluates to True, go on,
return eval_and(rest_exprs(exprs), env)
def eval_or(exprs, env, tail=True):
# If there is no expression to be evaluated, return True
if exprs is nil:
return False
# If the last expression is reached (indicating that the values of the
# previous expressions are all False), then the evaluation result is
# returned directly
elif rest_exprs(exprs) is nil:
return scheme_eval(first_expr(exprs), env, tail=tail)
value = scheme_eval(first_expr(exprs), env)
# If an expression evaluates to True, return value, and the remaining
# expressions are not evaluated
if is_scheme_true(value):
return value
else:
return eval_or(rest_exprs(exprs), env)
如上所示,and和or表示式都是短路(short-circuited)的。對於and表示式,如果其子表示式有求值為False的,則直接返回False;對於or表示式,如果其子表示式有求值為True的,直接返回True。
序列
eval_sequence()用在scheme_apply()裡,用於求值過程體裡的表示式序列。它也用在scheme_eval()裡,用於求值begin和let表示式內的表示式序列。這個過程以一個表示式序列和一個環境為引數,按照序列裡表示式出現的順序對它們進行求值,並返回最後一個表示式的值。
def eval_sequence(exprs, env, tail=False):
if not is_scheme_pair(exprs):
return
# If `exprs` is the last expression
if rest_exprs(exprs) is nil:
# The value of the last expression is returned as the value of the
# entire `begin` special form(or the body of a procedure)
return scheme_eval(first_expr(exprs), env, tail)
else:
# Evaluate the expressions <expr 1>, <expr 2>, ..., <expr k> in order
scheme_eval(first_expr(exprs), env)
return eval_sequence(rest_exprs(exprs), env, tail)
eval_begin()和eval_let()亦依據eval_sequence()來定義:
def eval_begin(exprs, env, tail=True):
validate_form(exprs, min=1)
return eval_sequence(exprs, env, tail)
def eval_let(exprs, env, tail=True):
validate_form(exprs, min=2)
let_env = make_let_env(first_expr(exprs), env)
return eval_sequence(rest_exprs(exprs), let_env, tail=tail)
賦值和定義
下面過程處理變數賦值,它先呼叫scheme_eval()求出需要賦的值,將變數和得到的值傳給env.set_variable_value()方法,將有關的值安置到環境env裡。
def eval_assignment(expr, env):
env.set_variable_value(assignment_variable(
expr), scheme_eval(assignment_value(expr), env))
變數定義也用類似方式處理:
def eval_definition(expr, env):
# Check that expressions is a list of length at least 2
validate_form(expr, min=2)
var = definition_varaible(expr)
val = definition_value(expr)
env.define_variable(var,
scheme_eval(val, env))
return var
Lambda表示式
對lambda表示式進行求值時(注意此時只是對lambda表示式的」定義「進行求值),我們會先分別獲取lambda表示式的形參和過程體,並結合lambda表示式定義時的環境來初始化LambdaProcedure物件(也即預設採用的基於詞法作用域規則)。
def eval_lambda(expr, env):
validate_form(expr, min=2)
parameters = lambda_parameters(expr)
validate_parameters(parameters)
body = lambda_body(expr)
return LambdaProcedure(parameters, body, env)
而對於我們額外新增的採用動態作用域的dlambda表示式,在初始化時則不會用到其定義時的環境。
def eval_dlambda_form(expr, env):
validate_form(expr, min=2)
parameters = expr.first
validate_parameters(parameters)
return DLambdaProcedure(parameters, expr.rest)
引號表示式
對quote表示式(即')進行求值時,直接返回其所參照的表示式本身即可(無需環境)。
def eval_quote(expr, env):
validate_form(expr, min=1, max=1)
return text_of_quotation(expr)
對quasiquote表示式(即 ` )進行求值則是一個遞迴的過程,在獲得了 ` 所參照的表示式後,我們需要掃描該表示式檢視是否有被unquote(即以,開頭)的子表示式,如果遇到了則對該子表示式求值,而其餘表示式則保持不求值狀態。比如(1 2 ,(+ 3 4)) 的求值結果為'(1 2 7)。注意這裡quasiquote內部可以巢狀多個quasiquote和unquote,故需要在遞迴時維護depth變數來表示被unquote操作「抵消」後剩餘的quasiquote深度。
def eval_quasiquote(expr, env):
def quasiquote_item(val, env, depth):
"""Evaluate Scheme expression `val` that is nested at depth `level` in
a quasiquote form in frame `env`."""
if not is_scheme_pair(val):
return val
# When encountering `unquote`, we decrease the depth by 1.
# If the depth is 0, we evaluate the rest expressions.
if is_tagged_list(val, "unquote"):
depth -= 1
if depth == 0:
expr = rest_exprs(val)
validate_form(expr, 1, 1)
return scheme_eval(first_expr(expr), env)
elif val.first == "quasiquote":
# Leave the item unevaluated
depth += 1
# Recursively quasiquote the items of the list
return val.map(lambda elem: quasiquote_item(elem, env, depth))
validate_form(expr, min=1, max=1)
# Note that when call `quasiquote_item`, we have encountered
# the first quasiquote, so depth=1
return quasiquote_item(text_of_quotation(expr), env, depth=1)
注意unquote操作是不能夠在quasiquote表示式之外進行的,如果在quasiquote之外對unquote進行求值,則會報對應的錯誤:
def eval_unquote(expr, env):
raise SchemeError("Unquote outside of quasiquote")
宏
對宏的定義,也即define-macro表示式進行求值時,我們選擇將表示式的形參、表示式體及環境都儲存到MacroProcedure物件中,而不立即進行求值操作求值。此外,我們還在環境中新增宏的名稱與MacroProcedure物件的繫結。
def eval_macro_definition(expr, env):
validate_form(expr, min=2)
target = expr.first
if is_scheme_pair(target) and is_scheme_symbol(target.first):
func_name = target.first
# `target.rest` is parameters,not `target.rest.first`
parameters = target.rest
body = expr.rest
# Just store the expression, rather than evaluate it
env.define_variable(func_name, MacroProcedure(parameters, body, env))
return func_name
else:
raise SchemeError("Invalid use of macro")
4.1.2 表示式的表示
這個求值器很像我們在部落格《SICP:符號求導、集合表示和Huffman樹(Python實現) 》中所討論的符號微分程式。這兩個程式完成的都是一些對符號表示式的操作。在這兩個程式中,對一個複合表示式的求值結果,也是由對錶示式片段的遞迴操作來確定的,且對該結果的組合方式也是由表示式的型別來確定。在這兩個程式中,我們都採用了資料抽象技術,將一般性的操作規則與表示式的表示方式進行了解耦(decouple)。在符號微分程式中,這意味著同一個微分程式可以處理字首(prefix)形式、中綴(infix)形式或其他形式的代數表示式。對於求值器,這意味著被求值語言的語法(syntax)僅僅由對錶示式進行分類和片段提取的過程來決定。
這裡需要提一下,我們求值器的輸入是以序對
Pair組成的表,也即經過詞法分析(lexical analysis)+語法分析(syntactic analysis)後所構建的抽象語法樹(abstract syntax tree, AST)。比如對於 Scheme表示式(+ (* 3 5) (- 10 6))其對應的表為:
Pair('+', Pair(Pair('*', Pair(3, Pair(5, nil))), Pair(Pair('-', Pair(10, Pair(6, nil))), nil)))事實上由於Scheme程式本身就可視作一棵AST,因此為Scheme程式寫用於語法分析的Parser異常簡單。我們可以通過
Pair物件的.first屬性存取其的第一個元素,.rest屬性存取其的後續元素。
下面是我們所要實現的Scheme語言的語法規範:
- 這裡的自求值表示式包括數、字串、
nil(也即空表'())、布林值和undefined(在Python中表示為None):
def is_self_evaluating(expr):
return is_scheme_boolean(expr) or is_scheme_number(expr) or \
is_scheme_null(expr) or is_scheme_string(expr) or expr is None
- 變數用符號表示:
def is_scheme_variable(x):
return is_scheme_symbol(x)
- 引號表示式的形式是
(quote <text-of-quotation>)(求值器看到的表示式是以quote開頭的表,即使這種表示式在輸入時用的是一個引號):
def text_of_quotation(expr):
return expr.first
def is_unquote(expr):
return is_tagged_list(expr, "unquote")
注意這裡對text_of_quotation()函數而言傳入的expr是不含標籤quote的,故直接使用expr.first來存取<text-of-quotation>即可。
is_unquote()函數借助函數is_tagged_list()來定義,它可用於確定一個表的開始是不是某個給定符號:
def is_tagged_list(expr, tag):
if is_scheme_pair(expr):
return expr.first == tag
else:
return False
注意我們這裡沒有is_quote()函數,這是因為對quote的型別判斷和其它特殊形式一樣,直接在scheme_eval()的分派過程中解決了。
- 賦值的形式是
(set! <var> <value>):
def assignment_variable(expr):
return expr.first
def assignment_value(expr):
return expr.rest.first
同樣,注意此處的expr不含標籤。
- 定義的形式是:
(define <var> <value>)
或者
(define (<var> <parameter 1>... <parameter n>)
<body>)
後一形式(標準的過程定義)只是下面形式的一種語法包裝:
(define <var>
(lambda (<parameter 1> ... <parameter n>)
<body>))
相應的語法函數是
def definition_varaible(expr):
target = expr.first
# For the case of (define <var> <value>)
if is_scheme_symbol(target):
# `(define x)` or `(define x 2 y 4)` is invalid
validate_form(expr, min=2, max=2)
return target
# For the case of (define (<var> <param 1>, ..., <param n>) <body>)
elif is_scheme_pair(target) and is_scheme_symbol(target.first):
return target.first
else:
bad_target = target.first if is_scheme_pair(target) else target
raise SchemeError("Non-symbol: {0}".format(bad_target))
def definition_value(expr):
target = expr.first
# For the case of (define <var> <value>)
if is_scheme_symbol(target):
return expr.rest.first
# For the case of (define (<var> <param 1>, ..., <param n>) <body>)
elif is_scheme_pair(target) and is_scheme_symbol(target.first):
# Note: The validation of the lambda special form is turned over
# to `scheme_eval()`
return make_lambda(target.rest, expr.rest)
else:
bad_target = target.first if is_scheme_pair(target) else target
raise SchemeError("Non-symbol: {0}".format(bad_target))
同樣,注意此處的expr不含標籤。
- lambda表示式是由符號
lambda開始的表:
def lambda_parameters(expr):
return expr.first
def lambda_body(expr):
return expr.rest
同樣,注意此處的expr不含標籤。
我們還為lambda表示式提供了一個建構函式,它用在上面的definition_value()裡。
def make_lambda(parameters, body):
return scheme_cons("lambda", scheme_cons(parameters, body))
- 條件表示式由
if開始,有一個謂詞部分,一個推論部分和一個(可缺的)替代部分。如果這一表示式沒有替代部分,我們就用False做為其替代。
def if_predicate(expr):
return expr.first
def if_consequent(expr):
return expr.rest.first
def if_alternative(expr):
return expr.rest.rest.first
我們也為if表示式提供了一個建構函式,它在cond_to_if中使用,用於將cond表示式變換為if表示式。
def make_if(predicate, consequent, alternative):
return scheme_list("if", predicate, consequent, alternative)
begin包裝起一個表示式序列。這裡我們設計選擇函數返回序列中的第一個表示式和其餘表示式。
def first_expr(seq):
return seq.first
def rest_exprs(seq):
return seq.rest
我們還設計了一個建構函式sequence_to_expr()(用在cond_to_if裡),它把一個序列變換為一個表示式,如果需要的話就加上begin作為開頭:
def sequence_to_expr(seq):
if seq is nil:
return seq
elif rest_exprs(seq) is nil:
return first_expr(seq)
else:
return make_begin(seq)
def make_begin(seq):
return scheme_cons("begin", seq)
let表示式在規約到用eval_sequence()對錶示式序列進行求值之前,需要新建環境。該新環境的建構函式下:
def make_let_env(bindings, env):
def bindings_items(bindings, env):
if bindings is nil:
return nil, nil
binding = bindings.first
validate_form(binding, min=2, max=2)
var = binding.first
val = scheme_eval(binding.rest.first, env)
vars, vals = bindings_items(bindings.rest, env)
return scheme_cons(var, vars), scheme_cons(val, vals)
if not is_scheme_list(bindings):
raise SchemeError("Bad bindings list in let form")
vars, vals = bindings_items(bindings, env)
validate_parameters(vars)
return env.extend_environment(vars, vals)
派生表示式
在一些語言中,一些特殊形式可以基於其他特殊形式的表示式定義出來,而不必直接去實現,比如cond表示式和let表示式。這樣採用語法變換的方式實現的表示式稱為派生表示式(derived expressions)。
cond表示式可以實現為一些巢狀的if表示式。例如,我們可以將對於下列表示式的求值問題:
(cond ((> x 0) x)
((= x 0) (display 'zero) 0)
(else (- x)))
規約為對下面涉及if和begin的表示式的求值問題:
(if (> x 0)
x
(if (= x 0)
(begin (display 'zero)
0)
(- x)))
採用這種方式實現對cond的求值能簡化求值器。
下面展示了提取cond表示式中各個部分的語法過程,以及函數cond_to_if(),它能將cond表示式變換為if表示式。一個分情況分析以cond開始,幷包含一個謂詞-動作子句的表。如果一個子句的符號是else,那麼就是一個else子句。
def cond_predicate(clause):
return clause.first
def cond_actions(clause):
return clause.rest
def cond_to_if(exprs):
return expand_clauses(exprs)
def expand_clauses(clauses):
# return None means that interpreter does not print anything
if clauses is nil:
return None
first = clauses.first
rest = clauses.rest
validate_form(first, min=1)
if cond_predicate(first) == "else":
if rest is nil:
return sequence_to_expr(first.rest)
else:
raise SchemeError(
"ELSE clause is not last: {0}".format(
repl_str(clauses)))
else:
if cond_actions(first) is nil: # for example, (cond ((= 1 1)))
# there is no consequent, we denote it as None
# o distinguish it from nil
if_consequent = None
else: # for example, (cond ((= 1 1) 2)) or (cond ((= 1 1) nil))
# there is a consequent, including nil
if_consequent = sequence_to_expr(first.rest)
return make_if(cond_predicate(first), if_consequent, cond_to_if(
rest))
4.1.3 求值器資料結構
除了需要定義表示式的外部語法之外,求值器的實現還必須定義好在其內部實際操作的資料結構,做為程式執行的一部分。例如序列資料結構,過程和環境的表示形式,真和假的表示方式等等。
序列資料結構
如我們在部落格《SICP: 層次性資料和閉包性質(Python實現)》中所言,序列資料結構由序對來進行層次化定義,序對的定義如下:
class Pair:
def __init__(self, first, rest):
self.first = first
self.rest = rest
def __len__(self):
n, rest = 1, self.rest
while isinstance(rest, Pair):
n += 1
rest = rest.rest
# The tail of the list must be nil
if rest is not nil:
raise TypeError("length attempted on improper list")
return n
def __eq__(self, p):
if not isinstance(p, Pair):
return False
return self.first == p.first and self.rest == p.rest
def map(self, fn):
mapped = fn(self.first)
if self.rest is nil or isinstance(self.rest, Pair):
return Pair(mapped, self.rest.map(fn))
else:
raise TypeError("ill-formed list (cdr is a promise)")
def flatmap(self, fn):
from primitive_procs import scheme_append
mapped = fn(self.first)
if self.rest is nil or isinstance(self.rest, Pair):
return scheme_append(mapped, self.rest.flatmap(fn))
else:
raise TypeError("ill-formed list (cdr is a promise)")
此外,我們還需要一個空表類及其範例:
class nil:
def __len__(self):
return 0
def map(self, fn):
return self
def flatmap(self, fn):
return self
nil = nil()
注意,nil範例將與其相同的類名進行了覆蓋,且該空表類自始至終只有一個範例,所以我們可以直接使用is nil語法來測試某個物件是否為空表。
謂詞檢測
為了實現條件表示式,我們把除了False物件之外的所有東西都接受為真:
def is_scheme_true(val):
return val is not False
def is_scheme_false(val):
return val is False
除了謂詞檢測之外,還有許多諸如is_scheme_pair()、is_scheme_list()之類的Scheme內建資料結構檢測函數,就不在此處進行一一列舉了,大家可直接參考我專案目錄下的primitive_procs.py檔案。
過程的表示
過程分為基本過程(primitive procedures)和複合過程(compound procedures,也即由define語句或lambda/dlambda語句定義的過程)。我們先定義基本過程如下:
class Procedure:
class PrimitiveProcedure(Procedure):
import primitive_procs as pprocs
def __init__(self, fn, name="primitive", use_env=False):
self.name = name
self.fn = fn
self.use_env = use_env
def apply(self, arguments, env):
if not self.pprocs.is_scheme_list(arguments):
raise self.pprocs.SchemeError(
"Arguments are not in a list: {0}".format(arguments))
# Convert a Scheme list to a Python list
arguments_list = self.flatten(arguments)
try:
if self.use_env:
return self.fn(*arguments_list, env)
return self.fn(*arguments_list)
except TypeError:
raise self.pprocs.SchemeError(
"Incorrect number of arguments: {0}".format(self))
def flatten(self, arguments):
if arguments is nil:
return []
else:
return [arguments.first] + self.flatten(arguments.rest)
下列函數可檢查過程是否為基本過程:
def is_primitive_procedure(procedure):
return isinstance(procedure, PrimitiveProcedure)
複合過程則包括形參parameters、過程體body和環境body:
class LambdaProcedure(Procedure):
import primitive_procs as pprocs
def __init__(self, parameters, body, env):
assert isinstance(env, Environment), "env must be of type Environment"
self.pprocs.validate_type(parameters, self.pprocs.is_scheme_list,
0, "LambdaProcedure")
self.pprocs.validate_type(
body, self.pprocs.is_scheme_list, 1, "LambdaProcedure")
self.parameters = parameters
self.body = body
self.env = env
def make_call_frame(self, arguments, env):
return self.env.extend_environment(self.parameters, arguments)
複合過程的make_call_frame()方法用於將複合過程物件應用於實參時,向過程定義時的環境self.env中新增一個新幀(注意不是呼叫時環境env,呼叫時環境env並未使用),從而擴充套件得到一個新的環境。具體的env.extend_environment()方法我們會在環境的表示部分再講述如何實現。
下列函數可檢查過程是否為複合過程:
def is_compound_procedure(procedure):
return isinstance(procedure, Procedure)
使用動態作用域的dlambda過程物件定義如下:
class DLambdaProcedure(Procedure):
def __init__(self, parameters, body):
self.parameters = parameters
self.body = body
def make_call_frame(self, arguments, env):
return env.extend_environment(self.parameters, arguments)
該過程也是複合過程,唯一的區別是在過程應用時,建立的新環境是基於呼叫時環境env來擴充套件的,而不是定義時環境。
環境的表示
求值器還需要定義對環境的表示。正如我們在部落格《SICP:求值和環境模型(Python實現)》中所說,一個環境就是一個幀的序列,每個幀都是一個包含繫結的表格,其中繫結關聯起一些變數和與之對應的值。
我們首先定義好幀:
class Frame:
def __init__(self):
self.bindings = {}
def add_binding(self, var, val):
self.bindings[var] = val
def set_var(self, var, val):
self.add_binding(var, val)
然後在幀的基礎之上定義好環境:
class Environment:
import primitive_procs as pprocs
def __init__(self):
self.frames = self.pprocs.scheme_list(Frame())
def lookup_variable_value(self, var):
...
def extend_environment(self, vars, vals):
...
def define_variable(self, var, val):
...
def set_variable_value(self, var, val):
...
和環境有關的方法lookup_variable_value()、extend_environment()、define_variable()、set_variable_value()我們在下面進行分別闡述。
lookup_variable_value()方法返回符號var在環境裡的繫結值,如果這一變數沒有繫結就發出一個錯誤訊號:
def lookup_variable_value(self, var):
def env_loop(frames):
# If cannot find the variable in the current environment
if self.pprocs.is_scheme_null(frames):
raise self.pprocs.SchemeError(
"Unbound variable: {0}".format(var))
frame = frames.first
if var in frame.bindings.keys():
return frame.bindings[var]
else:
return env_loop(frames.rest)
return env_loop(self.frames)
extend_environment()方法返回一個新環境,這個環境裡包含了一個新幀,其中所有位於表vars裡的符號繫結到表vals裡對應的元素,而該幀的外圍環境是當前這個物件所對應的環境。
def extend_environment(self, vars, vals):
new_env = Environment()
if len(vars) == len(vals):
new_env.frames = self.pprocs.scheme_cons(
self.make_frame(vars, vals),
self.frames)
elif len(vars) < len(vals):
raise self.pprocs.SchemeError(
"Too many arguemtns supplied")
else:
raise self.pprocs.SchemeError(
"Too few arguemtns supplied")
return new_env
@ staticmethod
def make_frame(vars, vals):
frame = Frame()
while isinstance(vars, Pair):
var = vars.first
val = vals.first
frame.add_binding(var, val)
vars = vars.rest
vals = vals.rest
return frame
define_variable()方法在當前物件所對應環境的第一個幀里加入一個新系結,它關聯起變數var和val。
def define_variable(self, var, val):
frame = self.frames.first
frame.add_binding(var, val)
set_variable_value()方法修改變數var在當前物件所對應環境裡的繫結,使得該變數現在繫結到值val。如果這一變數沒有繫結就發出一個錯誤訊號。
def set_variable_value(self, var, val):
def env_loop(frames):
# 空表
if self.pprocs.is_scheme_null(frames):
raise self.pprocs.SchemeError(
"Unbound variable: {0}".format(var))
frame = frames.first
if var in frame.bindings.keys():
frame.set_var(var, val)
return
else:
env_loop(frames.rest)
env_loop(self.frames)
不過需要注意的是,這裡所描述的方法,只不過是表示環境的許多方法之一。由於前面採用了資料抽象的技術,而這已經將求值器的其它部分與這些表示細節隔離開,因此如果需要的話我們也完全可以修改環境的表示。在產品質量的Lisp系統裡,求值器中環境操作的速度——特別是查詢變數的速度——對系統的效能有著重要的影響。這裡所描述的表示方式雖然在概念上非常簡單,但其工作效率卻很低,通常不會用在產品系統裡。其低效的原因來自求值器為了找到一個給定變數的繫結,需要搜尋許多個幀。這樣一種方式稱為深約束。避免這一低效性的方法是採用一種稱為語法作用域的策略,可參考原書5.5.6節。
4.1.4 作為程式執行這個求值器
有了一個求值器,我們手頭上就有了一個有關Lisp表示式如何求值的程式描述(這是用Python描述的)。接下來我們來看如何執行這個程式。
我們的求值器程式最終把表示式規約到基本過程的應用(基本過程的定義在專案程式碼中的primitive_procs.py檔案中)。而每個基本過程名都必須有一個繫結,以便當scheme_eval()求值一個應用基本過程的運運算元時,可以找到相應的物件,並呼叫這個物件的apply方法。為此我們必須建立起一個初始環境,在其中建立起基本過程的名字與一個唯一物件的關聯,在求值表示式時的過程中可能遇到這些名字。
def setup_environment():
initial_env = Environment()
initial_env.define_variable("undefined", None)
add_primitives(initial_env, PRIMITIVE_PROCS)
return initial_env
這裡的PRIMITIVE_PROCS是一個Python全域性變數,具體而言是一個儲存了基本過程函數及其名稱的表。基本過程物件的具體表示方式我們已經在上文中提到,也就是PrimitiveProcedure,因此我們可以用下列函數將基本過程名稱及其物件的繫結新增到全域性環境中:
def add_primitives(env, funcs_and_names):
for fn, name, use_env in funcs_and_names:
env.define_variable(name, PrimitiveProcedure(
fn, name=name, use_env=use_env))
為了能夠很方便地執行這個元迴圈求值器,我們使用函數read_eval_print_loop()來模擬Lisp中的讀入-求值-列印迴圈。這個迴圈列印出一個提示符(prompt),讀入輸入表示式,進行詞法分析和語法分析轉換為AST後,再在全域性環境裡求值這個表示式,而後列印出得到的結果。
def read_eval_print_loop(env, infile_lines=None, interactive=False,
quiet=False, startup=False, load_files=(),
report_errors=False, print_ast=False):
if startup:
for filename in load_files:
scheme_load(filename, True, env)
# Initialize a tokenizer instance
tokenizer = Tokenizer()
# Initialize a parser instance
parser = Parser()
while True:
try:
lines_stream = read_input(infile_lines, input_prompt="scm> ")
# Tokenize the input lines
lines_stream = (tokenizer.tokenize(line) for line in lines_stream)
# Parse a single expression / multiple expressions util all the
# tokens are consumed
while True:
# Parse a complete expression (single-line or multi-line) at a
# time
ast = parser.parse(lines_stream)
result = scheme_eval(ast, env)
if not quiet:
print(repl_str(result))
# If all the tokens read are consumed, then break
if parser.is_empty():
break
except (SchemeError, SyntaxError, ValueError, RuntimeError) as err:
...
def read_input(infile_lines, input_prompt):
if infile_lines: # If use a file stream as input
while infile_lines:
line = infile_lines.pop(0).strip("\n")
yield line
raise EOFError
else: # if use a keyboard stream as input
while True:
yield input(input_prompt)
# If a multi-line expression input is not
# terminated, use whitespace as the
# the input prompt to read more lines.
input_prompt = " " * len(input_prompt)
為了執行這個求值器,現在我們需要著的全部事情就是初始化這個全域性環境,並啟動上述的讀入-求值-列印迴圈。
def main():
args = parse_args()
sys.path.insert(0, "")
interactive = True
load_files = []
if args.load:
for filename in args.filenames:
load_files.append(filename)
the_global_env = setup_environment()
read_eval_print_loop(env=the_global_env, startup=True,
interactive=interactive, load_files=load_files,
print_ast=args.ast)
下面是一個互動過程範例:
scm> (define (make-withdraw balance)
(lambda (amount)
(If (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds")))
make-withdraw
scm> (define W1 (make-withdraw 100))
w1
scm> (define W2 (make-withdraw 100))
w2
scm> (W1 50)
50
scm> (W2 70)
30
scm> (W2 40)
"Insufficient funds"
scm> (W1 40)
10
4.1.5 將資料作為程式
在思考求值Lisp表示式的Python程式時,有一個類比可能很有幫助。關於程式意義的一種操作式觀點(operational view),就是將程式看做是一種抽象的(可能無窮大的)機器的一個描述。比如考慮下面的Lisp求階乘程式:
(define (factorial n)
(if (= n 1)
1
(* (factorial (- n 1)) n)))
我們可以將這一程式看成一部機器的描述。這部機器包含的部分有遞減(decrement)、乘法(multiply)以及相等測試(tests for equality),還有一個兩位開關(即if分支)和另一部階乘機器(這樣,階乘機器就是無窮的,因為其中包含著另一部階乘機器)。下圖是這部階乘機器的流程圖,說明了有關的部分如何連線在一起。

按照類似的方式,我們也可以把求值器看做是一部非常特殊的機器,它要求以一部機器的描述作為輸入。給定了這個輸入之後,求值器就能夠規劃自己的行為(configures itself)來模擬被描述的機器。舉例來說,如果我們將factorial過程的定義送入求值器,求值器能夠計算階乘,如下圖所示:

按照這一觀點,我們的求值器可以被看做是是一種通用機器(universal machine)。它能夠模擬其它的任何機器,只要它們已經被描述為Lisp程式。這是非常驚人的。比如我們為電子電路設想一種類似的求值器,這將會是一種電路,它以另一個電路(例如某個濾波器)的訊號編碼方案做為輸入。在給了它這種輸入之後,這一電路求值器能具有與這一描述所對應的濾波器同樣的行為。這樣的一個通用電子線路將會難以想象的複雜,而程式的求值器卻是一個相當簡單的程式。
事實上,任一求值器都能模擬其他的求值器。這樣,有關「原則上說什麼可以計算」(忽略掉有關所需時間和空間的實踐性問題)的概念就與語言或計算機無關了,它反映的是一個有關可計算性(computability) 的基本概念。這一思想第一次是由圖靈以清晰的方式闡述,他在1936年的論文《論可計算數及其在判定性問題上的應用》[2]為理論電腦科學奠定了基礎。在這篇論文裡,圖靈給出了一種簡單的計算模型——現在被稱為圖靈機——並聲稱,任何「有效過程」都可以描述為這種機器的一個程式(這一論斷就是著名的邱奇—圖靈論題)。圖靈而後實現了一臺通用機器,即一臺圖靈機,其行為就像是所有圖靈機程式的求值器。
求值器的另一驚人方面,在於它就像是在我們的程式設計語言所操作的資料物件和這個程式設計語言本身之間的一座橋樑。現在設想這個用Python實現的求值程式正在執行,一個使用者正在輸入表示式並觀察所得到的結果。從使用者的觀點看,他所輸入的形如(* x x)的表示式是程式設計語言裡的一個表示式,是求值器將要執行的東西。而從求值器的觀點看,這一表示式不過是一個表(這裡就是三個符號*、x和x的表),它所要做的也就是按照一套定義良好的規則去操作這個表。
這種使用者程式即求值器的資料的情況,未必會成為混亂之源。事實上,有時簡單地忽略這種差異,為使用者提供顯式地將資料物件當做Lisp表示式求值的能力,允許他們在程式裡直接使用eval,甚至可能帶來許多方便。在我們實現的這個求值器裡,就可以直接使用eval過程:
scm> (eval '(* 5 5))
25
scm> (eval (cons '* (list 5 5)))
25
事實上,Python語言中也內建了eval()函數:
>>> eval("5 * 5")
25
參考
- [1] Abelson H, Sussman G J. Structure and interpretation of computer programs[M]. The MIT Press, 1996.
- [2] Turing A M. On computable numbers, with an application to the Entscheidungsproblem[J]. J. of Math, 1936, 58(345-363): 5.