編譯原理（前端）的演演算法和實現

本文介紹從零實現Lex+YACC（即一鍵生成編譯器（前端））的演演算法。完整程式碼在（https://gitee.com/bitzhuwei/grammar-mentor）和（https://github.com/bitzhuwei/GrammarMentor）。

下文將用「解析器」指代編譯器前端（即詞法分析和語法分析）。

本文主要以四則運算為例，其文法如下：

// GrammarName = Calc
// ExtractedType = FinalValue
Additive       : Additive '+' Multiplicative // R[0]
               | Additive '-' Multiplicative // R[1]
               | Multiplicative ; // R[2]
Multiplicative : Multiplicative '*' Primary // R[3]
               | Multiplicative '/' Primary // R[4]
               | Primary ; // R[5]
Primary        : '(' Additive ')' // R[6]
               | 'number' ; // R[7]
// 用 %%xxx%% 格式 描述單詞
'number'       : %%[0-9]+%% ; // 為便於演示，僅處理正整數

本文按如下順序進行：

手工實現四則運算Calc的解析器CompilerCalc。
總結出文法的文法Grammar。
手工實現文法的解析器CompilerGrammar。
用CompilerGrammar一鍵生成CompilerCalc。
用CompilerGrammar一鍵生成CompilerGrammar。

練手預熱——四則運算解析器`CompilerCalc`

從原始檔內容string到單詞流TokenList到語法樹Node到語意結構TExtracted，是各種解析器共同的處理過程。

如果從原始檔讀到的內容是46*(87-19)，我預想中的CompilerCalc會逐步給出如下的資料：

// 原始檔內容string:
46*(87-19)
// 詞法分析的結果：單詞流TokenList:
T[0]='number' 46 [ln:1, col:1, i:0, L:2]
T[1]='*' * [ln:1, col:3, i:2, L:1]
T[2]='(' ( [ln:1, col:4, i:3, L:1]
T[3]='number' 87 [ln:1, col:5, i:4, L:2]
T[4]='-' - [ln:1, col:7, i:6, L:1]
T[5]='number' 19 [ln:1, col:8, i:7, L:2]
T[6]=')' ) [ln:1, col:10, i:9, L:1]
// 語法分析的結果：語法樹Node:
R[2]=Additive : Multiplicative ; T[0->6]
 └─R[3]=Multiplicative : Multiplicative '*' Primary ; T[0->6]
    ├─R[5]=Multiplicative : Primary ; T[0]
    │  └─R[7]=Primary : 'number' ; T[0]
    │     └─T[0]='number' 46
    ├─T[1]='*' *
    └─R[6]=Primary : '(' Additive ')' ; T[2->6]
       ├─T[2]='(' (
       ├─R[1]=Additive : Additive '-' Multiplicative ; T[3->5]
       │  ├─R[2]=Additive : Multiplicative ; T[3]
       │  │  └─R[5]=Multiplicative : Primary ; T[3]
       │  │     └─R[7]=Primary : 'number' ; T[3]
       │  │        └─T[3]='number' 87
       │  ├─T[4]='-' -
       │  └─R[5]=Multiplicative : Primary ; T[5]
       │     └─R[7]=Primary : 'number' ; T[5]
       │        └─T[5]='number' 19
       └─T[6]=')' )
// 語意分析的結果：extracted:
3128 = 46 * ( 87 - 19 )

詞法分析器

我設定，用'xxx'的形式表示Token，也就是用'前後包圍起來。

詞法分析的原理是自動機/狀態機。自動機可以用正規表示式來表示。

上文中的[0-9]+是一個正規表示式，表示「1個或多個0到9」，也就是0或正整數。Lex的主要功能就是將字串格式的正規表示式轉化為自動機，再將自動機轉為等價的程式碼形式。

我設定，描述Token的正規表示式，用%%前後包圍起來。

如果文法中的某個Token沒有明示其正規表示式，那麼它的字面本身就是它的正規表示式。準確來說，它的字面本身就是它的正規表示式的內容（在涉及跳脫字元時會有區別）。例如'+'和'('，它們隱含的正規表示式分別是%%[+]%%和%%(%%。當然，%%[+]%%可以換為%%\+%%或%%\u002B%%。

我們可以手工畫出識別Calc文法的全部Token的自動機。

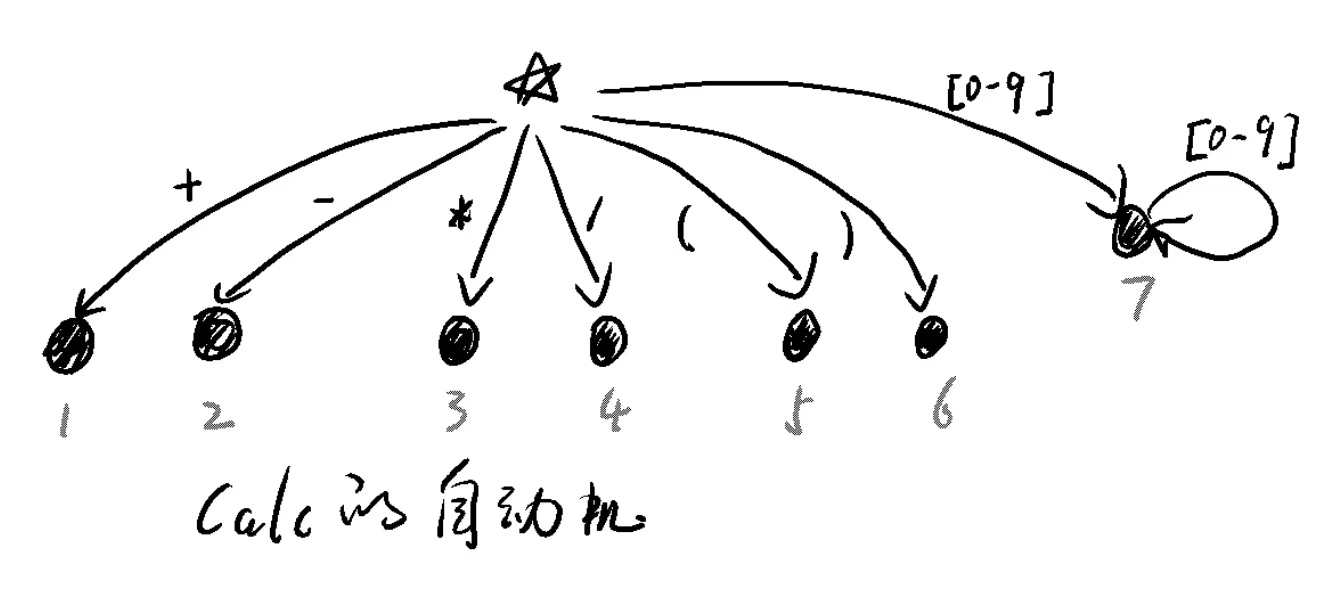
圖中的☆代表初始狀態initialState。

以圖中的狀態7為例：

對於一個沒有詞法錯誤的原始檔，當詞法分析器讀入的char是[0-9]中的某個時，就可以斷定接下來會遇到的是一個'number'型別的Token，並進入它的終止狀態7；
之後可以繼續收集此Token的內容；
當讀到一個不屬於[0-9]的char時，會從終止狀態7返回initialState。也就是說，對於每個狀態A，都有一條沒有被畫出來的邊，從狀態A指向initialState；initialState本身也是如此。有的文章將這種狀態稱為「死狀態」。有死就有生，有生就有死。死就是生，生就是死。「死狀態」就是初始狀態☆。

現在我們手工將此自動機轉化為C#程式碼。

對於initialState，也就是lexicalState0：

private static readonly LexicalState lexicalState0 = new LexicalState(
    new LexicalRule(/* ☆ --> 1 */
    currentChar => currentChar == '+',
    context => {
        BeginToken(context, EType.@Plus);
        ExtendToken(context);
        return lexicalState1; // go to state 1
    }),
    new LexicalRule(/* ☆ --> 2 */
    currentChar => currentChar == '-',
    context => {
        BeginToken(context, EType.@Dash);
        ExtendToken(context);
        return lexicalState2; // go to state 2
    }),
    new LexicalRule(/* ☆ --> 3 */
    currentChar => currentChar == '*',
    context => {
        BeginToken(context, EType.@Asterisk);
        ExtendToken(context);
        return lexicalState3; // go to state 3
    }),
    new LexicalRule(/* ☆ --> 4 */
    currentChar => currentChar == '/',
    context => {
        BeginToken(context, EType.@Slash);
        ExtendToken(context);
        return lexicalState4; // go to state 4
    }),
    new LexicalRule(/* ☆ --> 5 */
    currentChar => currentChar == '(',
    context => {
        BeginToken(context, EType.@LeftParenthesis);
        ExtendToken(context);
        return lexicalState5; // go to state 5
    }),
    new LexicalRule(/* ☆ --> 6 */
    currentChar => currentChar == ')',
    context => {
        BeginToken(context, EType.@RightParenthesis);
        ExtendToken(context);
        return lexicalState6; // go to state 6
    }),
    new LexicalRule(/* ☆ --> 7 */
    currentChar => '0' <= currentChar && currentChar <= '9',
    context => {
        BeginToken(context, EType.@number);
        ExtendToken(context);
        return lexicalState7; // go to state 7
    }),
    new LexicalRule(/* ☆ --> ☆ */
    currentChar => IsOther(currentChar),/*非以上字元*/
    context => {
        char c = context.CurrentChar;
        if (c == ' ' || c == '\r' || c == '\n' || c == '\t' || c == '\0') { return lexicalState0; }
        // default handler: unexpected char.
        var token = new Token(context.Cursor, context.Line, context.Column);
        token.value = c.ToString(); token.type = EType.Error;
        context.result.Add(token);
        return lexicalState0; // go to state 0
    })
);

一鍵生成的版本在此（https://gitee.com/bitzhuwei/grammar-mentor/blob/master/Practices/Practice.GeneratedXxxFormat.Test/GeneratedCalc/LexicalAnalyzer/DFA/CompilerCalc.LexicalState0.gen.cs#L10）

對於狀態7：

private static readonly LexicalState lexicalState7 = new LexicalState(
    new LexicalRule(/* 7 --> 7 */
    currentChar => '0' <= currentChar && currentChar <= '9',
    context => {
        ExtendToken(context);
        return lexicalState7; // go to state 7
    }),
    new LexicalRule(/* 7 --> ☆ */
    currentChar => IsOther(currentChar),/*非數位*/
    context => {
        AcceptToken(context, EType.@number);
        return lexicalState0; // go to state 0
    })
);

一鍵生成的版本在此（https://gitee.com/bitzhuwei/grammar-mentor/blob/master/Practices/Practice.GeneratedXxxFormat.Test/GeneratedCalc/LexicalAnalyzer/DFA/CompilerCalc.LexicalState1.gen.cs）

自動機與程式碼是一一對應的。其他狀態不再重述。

呼叫自動機的過程是所有解析器通用的，因此應當獨立出一個基礎類庫：

public TokenList Analyze(string sourceCode) {
    var context = new LexicalContext(sourceCode, this.initialState);
    while (!context.EOF) {
        char currentChar = context.CurrentChar;
        Func<LexicalContext, LexicalState> function = context.GetFunction(currentChar);
        LexicalState nextState = function(context);
        context.currentState = nextState;// prepare the current state to meet with next char.
        context.MoveForward();// move cursor to next char
    }
    // finish lexical analyzing with external char('\0').
    {
        char currentChar = context.CurrentChar;
        Func<LexicalContext, LexicalState> function = context.GetFunction(currentChar);
        LexicalState nextState = function(context);
        // practically not needed.
        context.currentState = nextState;// prepare the current state to meet with next char.
        context.MoveForward();// move cursor to next char
    }

    return context.result;
}

用'\0'收尾，是一個程式設計處理的小技巧。在語法分析時，也會用到類似的技巧。

完整版本在此（https://gitee.com/bitzhuwei/grammar-mentor/blob/master/bitzhuwei.Compiler/LexicalAnalyzer/LexicalAnalyzer.cs#L33）

語法分析器

文法裡都有什麼

我按下圖所示稱呼文法中的各個部分：

回看上文預想中的語法樹，可知，每個語法樹的葉結點，都對應一個Token。如果按後序優先遍歷的方式過一遍語法樹，就可以得到依索引排列的TokenList。這說明，語法樹是對TokenList的進一步組織，語法樹的葉結點型別與Token型別完全重合，非葉結點型別則是自己獨有的。

本文用Vt(terminal)表示葉結點，用Vn(non-terminal)表示非葉結點，用V表示兩者的總和。

語法分析三大件

nullable(VList)

如果一個V可能推匯出空ε，也就是說，一個Vt都沒推出來，那麼我們就說它是可空的，即nullable(V)=true。

如果一串V可能推匯出空ε，也就是說，一個Vt都沒推出來，那麼我們就說它是可空的，即nullable(V1 V2 V3 ..)=true。

顯然，對於任何Vt，nullable(Vt)=false。

FIRST(VList)

一個V，它能推出的第一個Vt都有誰呢？這些Vt合起來，就是FIRST(V)。

一串V，它能推出的第一個Vt都有誰呢？這些Vt合起來，就是FIRST(V1 V2 V3 ..)。

顯然，FIRST(V1 V2 V3 ..)包含FIRST(V1)；如果nullable(V1)=true，那麼FIRST(V1 V2 V3 ..)也包含FIRST(V2)；以此類推。

如果nullable(VList)=true，那麼FIRST(VList)包含空ε。

FOLLOW(Vn)

在所有的Regulation中，緊跟在Vn後面的Vt都有哪些？這就是FOLLOW(Vn)。

顯然，在left : 某V 某V .. Vn V1 V2 .. ;中，FOLLOW(Vn)包含FIRST(V1 V2 ..)；如果FIRST(V1 V2 ..)包含空ε，那麼FOLLOW(Vn)包含FOLLOW(left)。

LL(1)分析法

以下面的文法SAB為例：

S : A 'a' 's' // R[0]
  | B 'b' 's' // R[1]
  | 'd' ; // R[2]
A : 'a' ; // R[3]
B : 'c' // R[4]
  | empty ; // R[5] empty means (ε)

對於一個沒有語法錯誤的TokenList，如果語法分析器讀入的第一個Token是'a'，就可以斷定應當使用R[0]展開/推導，因為在R[0]、R[1]、R[2]中，只有R[0]的FIRST(A 'a' 's')包含'a'，也就是說，只有R[0]能匹配一個內容為'a' Vt1 Vt2 ..的TokenList；如果用R[1]或R[2]，就不可能使第一個Vt為'a'了。

抽象化地說，只要語法分析器讀入一個Token，就可以根據它的型別斷定，應當使用哪個Regulation。憑什麼呢？就憑對於當前結點（上例中是S）的所有Regulaion，FIRST(R[0])、FIRST(R[1])、FIRST(R[2])全都沒有交集。

這就是LL(1)文法的核心思想。這與詞法分析器有相似之處。

對於上面這個文法，可以用LL(1)分析法。但Calc文法不能用LL(1)分析，因為

FIRST( Additive '+' Multiplicative ) = { '(' 'number' }
FIRST( Additive '-' Multiplicative ) = { '(' 'number' }
FIRST( Multiplicative '\*' Primary ) = { '(' 'number' }

各個Regulation的FIRST集都有共同的Vt（即'('和'number'）。當詞法分析器讀到一個'number'時，它該用哪個Regulation展開/推導呢？它不知道呀。

LR(0)分析法

以Calc的原始檔46*(87-19)為例：

最初，我左手上是第一個Vn（Additive）；右手上是一個沒有語法錯誤的TokenList，也就是未來的Vt串。

我只在最抽象的程度上知道：這個Additive對應著整個TokenList（即T[0->6]）。

現在，我需要讓Additive具體地對應上TokenList，也就是逐步地展開/推導它，也就是具體化。

Additive有3個Regulation，每個都對應一個展開/推導的可能路線。問題是，選哪個？

從左手上看，我面對是的一個抽象的Vt串；從右手上看，我面對的是一個具體的Vt串。

從左手上看，我位於抽象的Vt串的開頭；從右手上看，我位於具體的Vt串的開頭。

觀察左手，由於R[0]、R[1]、R[2]的存在，實際上我是位於Additive '+' Multiplicative的開頭或Additive '-' Multiplicative的開頭或Multiplicative的開頭，也就是Additive的開頭或Multiplicative的開頭。這就向具體化邁進了一步。

繼續觀察Multiplicative，由於R[3]、R[4]、R[5]的存在，實際上我是位於Multiplicative '*' Primary的開頭或Multiplicative '/' Primary的開頭或Primary的開頭，也就是Multiplicative的開頭或Primary的開頭。這就又向具體化邁進了一步。

繼續觀察Primary，由於R[6]、R[7]的存在，實際上我是位於'(' Additive ')'的開頭或'number'的開頭，也就是說，我直接面對的是'('或'number'。這就又向具體化邁進了一步。由於'('和'number'是Vt，就沒有繼續展開的可能了。

像用放大鏡觀察物體一樣，我們一級一級地放大觀察當前直接面對的Vn，直至沒有Vn可放大。這個過程，就是求解閉包（Closure）的演演算法。之所以閉包中的各個項(Item)算作處於同一狀態，是因為它們本來就在描述同一狀態，只不過是在不同的放大級別上描述同一狀態。

此時已經能夠斷定，我們首先面對的，只會是'('或'number'。

如果語法分析器讀入的第一個Token是'('，那麼可以立即斷定，應當選擇R[6]展開/推導。此時，我將移進（shift-in）到Primary : '(' ⏳ Additive ')'中的⏳處，意思是，我讀到了'('，我期待著讀到Additive ')'。這提示我們，在讀入第一個Token之前，我們是位於如下圖所示的⏳處：

syntaxState0
[-1] FinalValue> : ⏳ Additive ; 
[0] Additive : ⏳ Additive '+' Multiplicative ; 
[1] Additive : ⏳ Additive '-' Multiplicative ; 
[2] Additive : ⏳ Multiplicative ; 
[3] Multiplicative : ⏳ Multiplicative '*' Primary ; 
[4] Multiplicative : ⏳ Multiplicative '/' Primary ; 
[5] Multiplicative : ⏳ Primary ; 
[6] Primary : ⏳ '(' Additive ')' ; 
[7] Primary : ⏳ 'number' ;

圖中的[-1]是為了便利程式設計新增的額外起始Regulation，也就是後文將介紹的擴充套件Regulation。

仿照上面的步驟，可以找到 Primary : '(' ⏳ Additive ')'的閉包，也就是：

syntaxState4
[6] Primary : '(' ⏳ Additive ')' ; 
[0] Additive : ⏳ Additive '+' Multiplicative ; 
[1] Additive : ⏳ Additive '-' Multiplicative ; 
[2] Additive : ⏳ Multiplicative ; 
[3] Multiplicative : ⏳ Multiplicative '*' Primary ; 
[4] Multiplicative : ⏳ Multiplicative '/' Primary ; 
[5] Multiplicative : ⏳ Primary ; 
[6] Primary : ⏳ '(' Additive ')' ; 
[7] Primary : ⏳ 'number' ;

如果語法分析器讀入的第一個Token是'number'，那麼可以立即斷定，應當選擇R[7]展開/推導。此時，我將移進到Primary : 'number' ⏳ ;中的⏳處。注意，此處是R[7]的末尾，也就是說，實際上我們已經讀入了這個R[7]對應的全部Vt，那麼此時就應當用R[7]進行規約（Reduction）了，也就是說，應當建造這樣的樹結構：

R[7]=Primary : 'number' ; T[0]
 └─T[0]='number' 46

剛剛，我直接面對的是'number'；現在，我直接面對的是它的上級Primary。當syntaxState0遇到Primary時，[5] Multiplicative : ⏳ Primary ;這一放大級別訴我們，應當跳入（Goto）Multiplicative : Primary ⏳ ;這個狀態。

繼續求閉包，繼續移進/規約，直至沒有新的syntaxState出現，LR(0)分析法的語法分析表就形成了，如下圖所示。這個過程就是LR(0)分析表的構造演演算法。

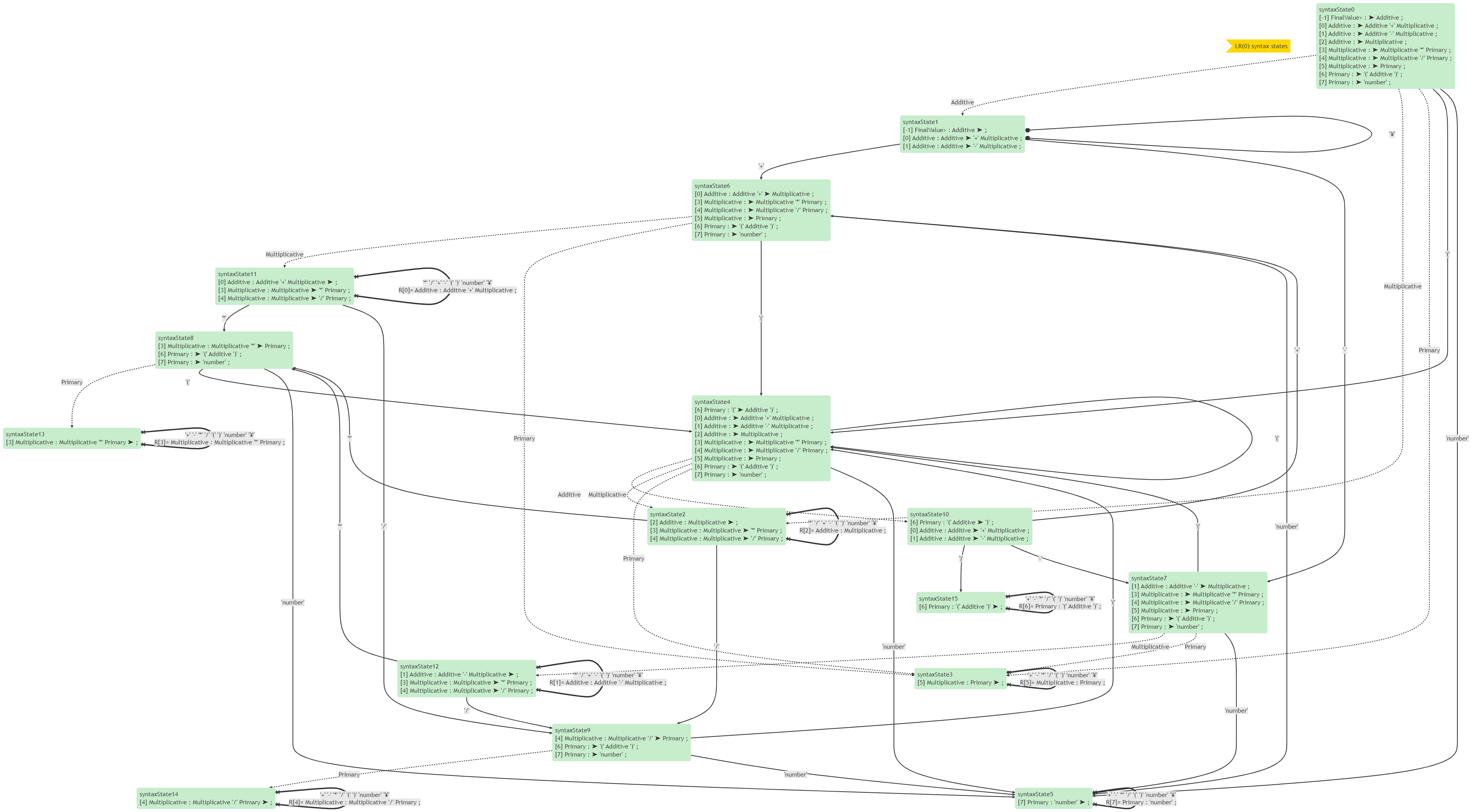
也可以用表格表示：

狀態	'+'	'-'	'*'	'/'	'('	')'	'number'	'￥'	Additive	Multiplicative	Primary
0					S4		S5		G1	G2	G3
1	S6	S7						完成
2	R[2]	R[2]	S8 R[2]	S9 R[2]	R[2]	R[2]	R[2]	R[2]
3	R[5]	R[5]	R[5]	R[5]	R[5]	R[5]	R[5]	R[5]
4					S4		S5		G10	G2	G3
5	R[7]	R[7]	R[7]	R[7]	R[7]	R[7]	R[7]	R[7]
6					S4		S5			G11	G3
7					S4		S5			G12	G3
8					S4		S5				G13
9					S4		S5				G14
10	S6	S7				S15
11	R[0]	R[0]	S8 R[0]	S9 R[0]	R[0]	R[0]	R[0]	R[0]
12	R[1]	R[1]	S8 R[1]	S9 R[1]	R[1]	R[1]	R[1]	R[1]
13	R[3]	R[3]	R[3]	R[3]	R[3]	R[3]	R[3]	R[3]
14	R[4]	R[4]	R[4]	R[4]	R[4]	R[4]	R[4]	R[4]
15	R[6]	R[6]	R[6]	R[6]	R[6]	R[6]	R[6]	R[6]

其中的第一行0和列'('對應的內容為S4，表示在狀態0讀到'('型別的Vt時，應當移進並進入狀態4。

其中的第一行0和列Additive對應的內容為G1，表示在狀態0遇到Additive型別的Vn時，應當跳入狀態1。

其中的第三行2和列'+'對應的內容為R[2]，表示在狀態2遇到'+'型別的Vt時，應當用R[2]規約。

其中的列'￥'表示額外的結束符，其作用類似詞法分析中最後額外新增的檔案結束符'\0'。讀到此Vt就表示整個TokenList已讀完。

從表格中可以看到，有的狀態下，既可以移進，也可以規約。這是語法衝突。這說明Calc不能用LR(0)分析法。

例如，用Calc解析123+456*789：

讀入'number'：從狀態0移進到狀態5；
狀態5規約：Primary : 'number' ;，回到狀態0；
從狀態0跳入狀態3；
狀態3規約：Multiplicative : Primary ;，回到狀態0；
從狀態0跳入狀態2；
狀態2規約：Additive : Multiplicative ;，回到狀態0；
從狀態0跳入狀態1；
讀入'+'：從狀態1移進到狀態6；
讀入'number'：從狀態6移進到狀態5；
狀態5規約：Primary : 'number' ;，回到狀態6；
從狀態6跳入狀態3；
狀態3規約：Multiplicative : Primary ;，回到狀態6；
從狀態6跳入狀態11；★★★
讀入'*'：從狀態11移進到狀態8；
讀入'number'：從狀態8移進到狀態5；
狀態5規約：Primary : 'number' ;，回到狀態8；
從狀態8跳入狀態13
狀態13規約：Multiplicative : Multiplicative '*' Primary ;，回到狀態6；
從狀態6跳入狀態11
狀態11規約：Additive : Additive '+' Multiplicative ;，回到狀態0；
從狀態0跳入狀態1
完成，回到狀態0

注意上面標★★★的位置，狀態11應當移進下一個Vt呢還是規約成Additive並回到狀態0呢？

如果規約，那麼就是先計算123+456後與789相乘了，其含義就變成了(123+456)*789。作為人類，我們知道此時應當移進；但作為計算機，它是沒有這種認知的。計算機是沒有任何認知的。

有衝突的位置不止這一個，讀者可以自行尋找。

讀者可以嘗試下面的例子，看看能否用LR(0)分析法。適量的練習是快速理解複雜內容的不二法門。

A : A '+' B // [0]
  | 'a' ; // [1]
B : 'b' ; // [2]

完成練習後，可以在（https://www.cnblogs.com/bitzhuwei/p/ABB-readme-full.html）檢視答案。

SLR(1)分析法

繼續上面的例子，如果456後面跟的是'*'，那麼就應當移進，如果是'+'，那麼就應當規約。

理論化地說，在Calc文法中，當⏳位於Additive : Additive '+' Multiplicative ⏳ ;狀態，只有⏳後面緊跟的是FOLLOW(Addtive)中的Token型別時，才有可能「狀態11應當用R[0]規約」，否則就不可能。

這就是SLR(1)的核心思想，也是SLR(1)與LR(0)的唯一區別。S代表simple。

這樣，就可以減少一些R[n]的出現。Calc文法的SLR(1)分析表如下：

狀態	'+'	'-'	'*'	'/'	'('	')'	'number'	'￥'	Additive	Multiplicative	Primary
0					S4		S5		G1	G2	G3
1	S6	S7						完成
2	R[2]	R[2]	S8	S9		R[2]		R[2]
3	R[5]	R[5]	R[5]	R[5]		R[5]
4					S4		S5		G10	G2	G3
5	R[7]	R[7]	R[7]	R[7]		R[7]
6					S4		S5			G11	G3
7					S4		S5			G12	G3
8					S4		S5				G13
9					S4		S5				G14
10	S6	S7				S15
11	R[0]	R[0]	S8	S9		R[0]		R[0]
12	R[1]	R[1]	S8	S9		R[1]		R[1]
13	R[3]	R[3]	R[3]	R[3]		R[3]
14	R[4]	R[4]	R[4]	R[4]		R[4]
15	R[6]	R[6]	R[6]	R[6]		R[6]

可以發現，此表中沒有衝突了。這說明Calc是可以用SLR(1)方法分析的。

LR(1)分析法

對於下面的文法，SLR(1)分析表仍然有衝突：

// GrammarName = Assignment
// ExtractedType = Assignment2
S : L '=' R | R ;
L : '*' R | 'id' ;
R : L ;

這是描述C語言中常見的a = *p或*p = x或*p = **d語句的文法部分。

它的SLR(1)分析表如下：

狀態	'='	'*'	'id'	'￥'	S	L	R
0		S4	S5		G1	G2	G3
1				完成
2	S6 R[4]
3				R[1]
4		S4	S5			G8	G7
5	R[3]
6		S4	S5			G8	G9
7	R[2]
8	R[4]
9				R[0]

如表所示，在狀態2遇到'='時，仍舊存在衝突。

它的狀態圖如下：

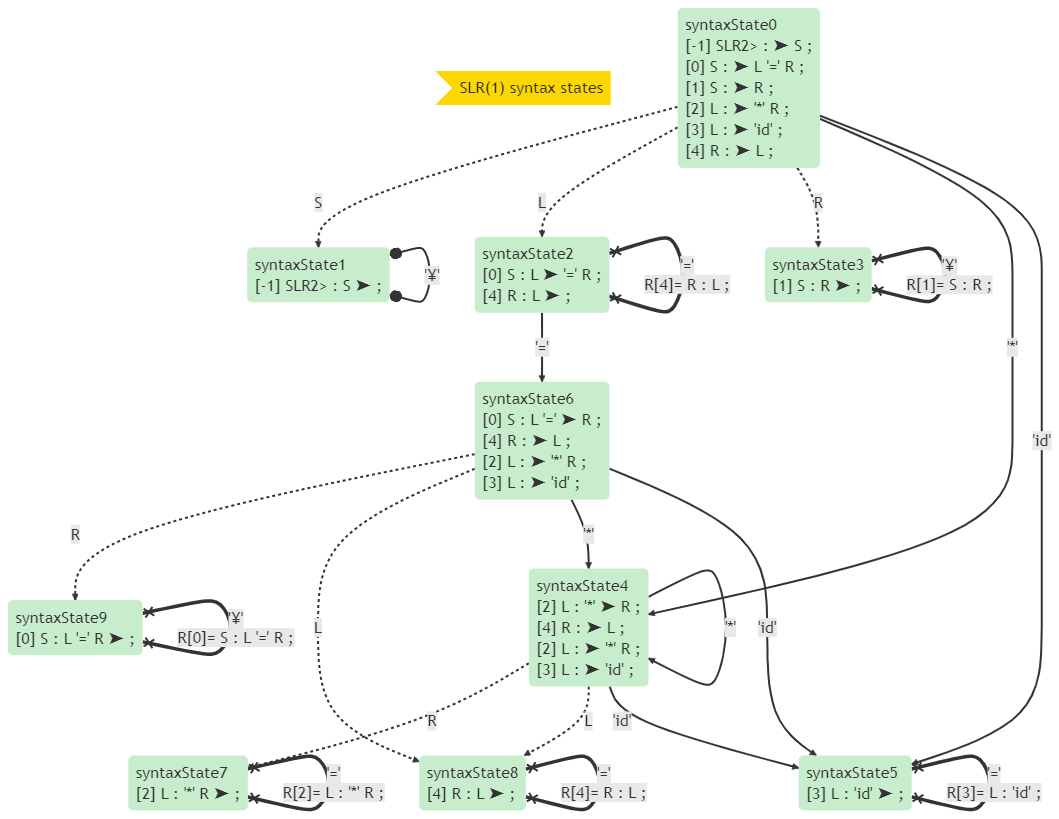
如圖所示，在狀態2遇到'='時，既可以按R[4]規約，又可以移進到狀態6。SLR(1)分析法無力解決這個衝突。

我們需要更細膩的分析法。

在認識LR(0)的閉包時，我們用放大鏡一級一級地展開⏳後面的Vn，但我們沒有管過：我們所在的Regulation對應的Vt串，緊跟著它的下一個Vt可能是什麼型別，可能是這個文法的所有Vt型別嗎？

當然不可能是。既然如此，我們應當在求解閉包的時候，把這個後面緊跟著的Token型別記錄下來。這個後面緊跟著的Token型別，被稱為lookAhead。這樣，當⏳位於某個Regulation的末尾，只有⏳後面是lookAhead時，才應當規約。

這就是LR(1)分析法的核心思想。在求解閉包時，除了像LR(0)一樣的操作外，還記錄了各個Regulation後面跟隨的Vt型別。這就是LR(1)與LR(0)的區別。

SLR(1)粗放地做了LR(1)的工作，因而適用範圍比LR(0)廣，比LR(1)窄。

上面的Assignment文法的LR(1)分析表如下：

狀態	'='	'*'	'id'	'￥'	S	L	R
0		S4	S5		G1	G2	G3
1				完成
2	S6			R[4]
3				R[1]
4		S4	S5			G8	G7
5	R[3]			R[3]
6		S11	S12			G10	G9
7	R[2]			R[2]
8	R[4]			R[4]
9				R[0]
10				R[4]
11		S11	S12			G10	G13
12				R[3]
13				R[2]

此表中就沒有衝突了，但狀態數量也增加了。它的狀態圖如下：

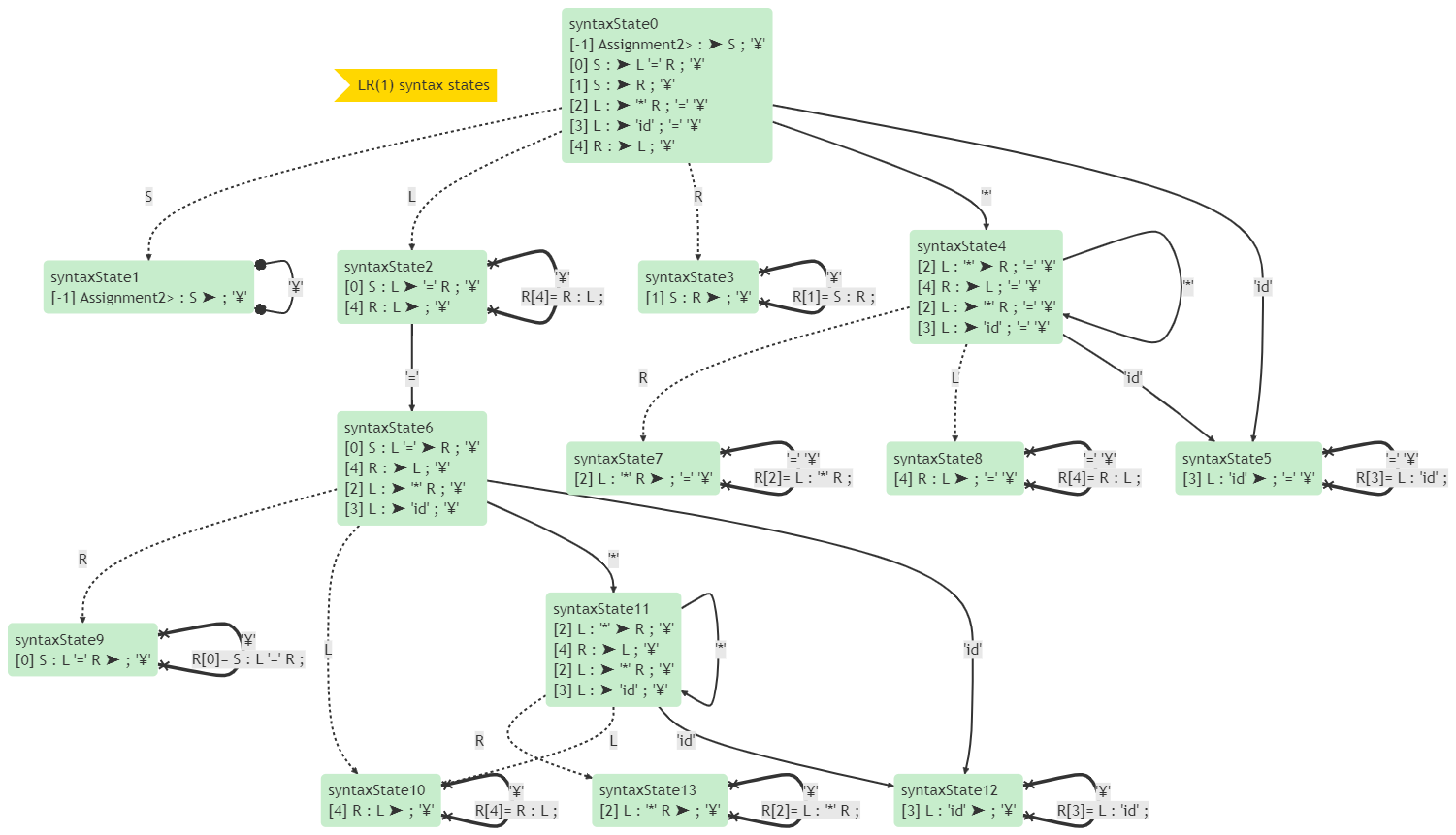
LR(1)分析法是我實現的適用範圍最廣的語法分析法。

LALR(1)分析法

LR(1)狀態的每個Item，都由Regulaiton、⏳的位置、跟隨的Vt（即lookAhead）這三條資料組成，其資訊詳盡，優點是適用範圍廣，缺點是它的狀態非常多，狀態包含的Item也非常多。在我處理GLSL Shader文法的時候，常常見到包含上萬個Item的LR(1)狀態。

兩個LR(1)狀態的Item，如果它們的Regulaiton相同、⏳的位置相同、只有lookAhead不同，我們也將這兩個Item視為相同。這就可以合併一些狀態。這樣，雖然在有的文法裡會產生衝突，但狀態的數量會大大減少。

這就是LALR(1)分析法的核心思想。很多程式語言，都可以用LALR(1)分析法進行語法分析。因此，它是很實用的優化技巧。

我們的Calc文法，可以用LALR(1)分析。它的LALR(1)分析表如下：

狀態	'+'	'-'	'*'	'/'	'('	')'	'number'	'￥'	Additive	Multiplicative	Primary
0					S4		S5		G1	G2	G3
1	S6	S7						完成
2	R[2]	R[2]	S8	S9		R[2]		R[2]
3	R[5]	R[5]	R[5]	R[5]		R[5]		R[5]
4					S4		S5		G10	G2	G3
5	R[7]	R[7]	R[7]	R[7]		R[7]		R[7]
6					S4		S5			G11	G3
7					S4		S5			G12	G3
8					S4		S5				G13
9					S4		S5				G14
10	S6	S7				S15
11	R[0]	R[0]	S8	S9		R[0]		R[0]
12	R[1]	R[1]	S8	S9		R[1]		R[1]
13	R[3]	R[3]	R[3]	R[3]		R[3]		R[3]
14	R[4]	R[4]	R[4]	R[4]		R[4]		R[4]
15	R[6]	R[6]	R[6]	R[6]		R[6]		R[6]

它的LALR(1)狀態圖如下：

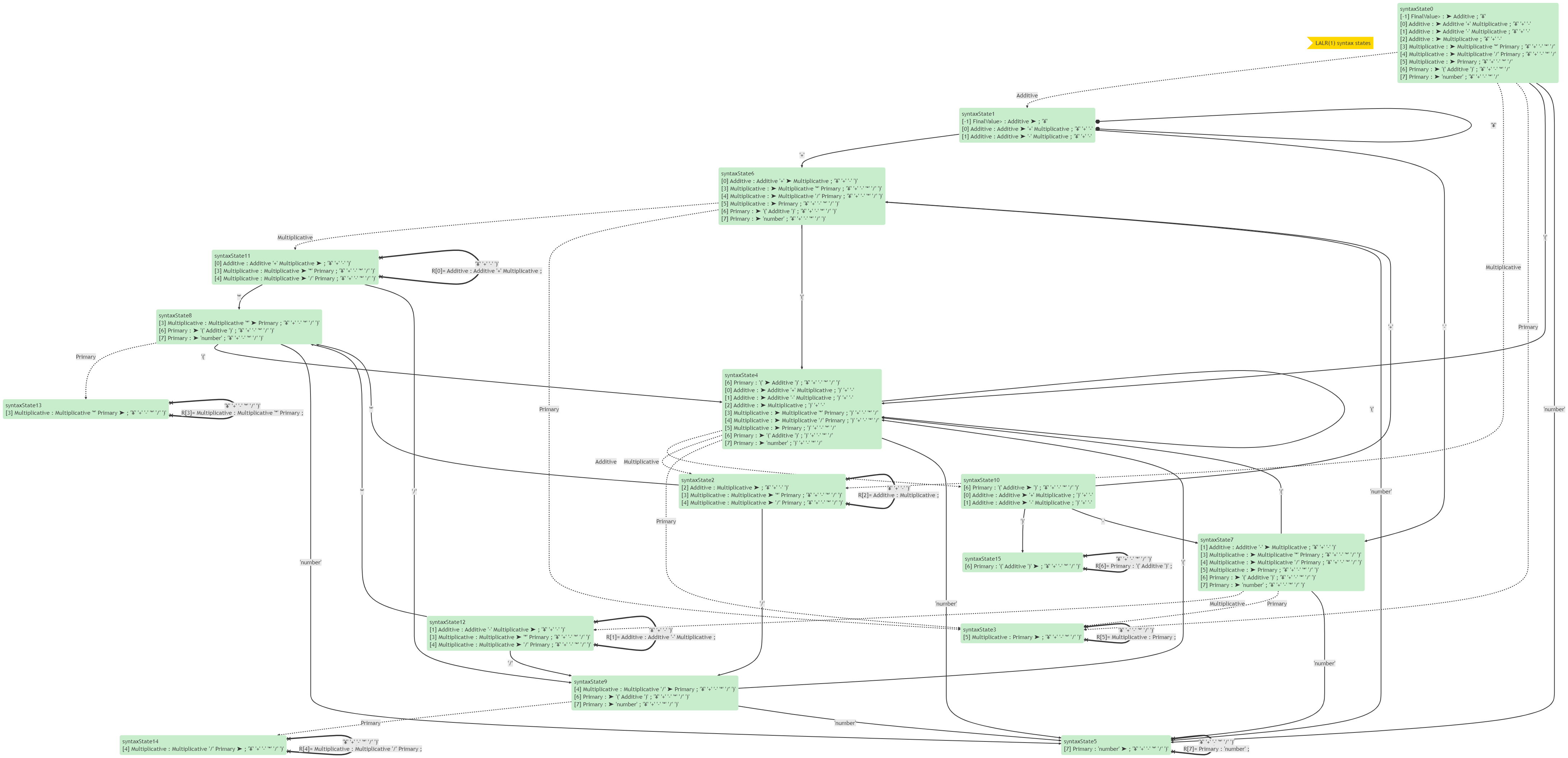
下面的文法用LALR(1)分析，就會產生衝突：

// GrammarName = LALR1Error
// ExtractedType = LALR1Error2
S : 'a' A 'd' | 'b' B 'd' | 'a' B 'e' | 'b' A 'e' ;
A : 'c' ;
B : 'c' ;

它的分析表如下：

狀態	'a'	'd'	'b'	'e'	'c'	'￥'	S	A	B
0	S2		S3				G1
1						完成
2					S6			G4	G5
3					S6			G8	G7
4		S9
5				S10
6		R[4] R[5]		R[5] R[4]
7		S11
8				S12
9						R[0]
10						R[2]
11						R[1]
12						R[3]

在分析表中可以看到，狀態6在遇到'd'或'e'時有衝突。

它的狀態圖如下：

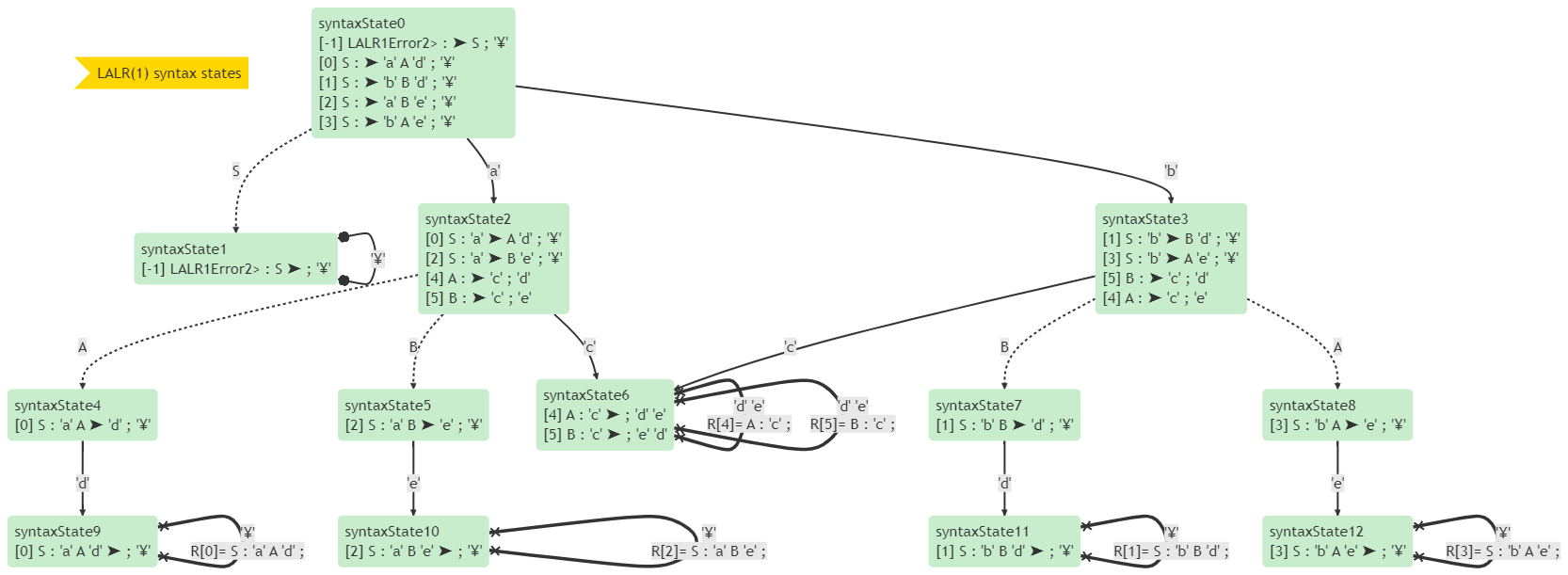
在狀態圖中也可以看到，狀態6在遇到'd'或'e'時可以按R[4]或R[5]進行規約。那到底是按R[4]規約還是按R[5]規約呢？它不知道呀。

LR分析法小結

從LR(0)到SLR(1)到LALR(1)到LR(1)，能夠解析的文法範圍逐步擴大，每一個分析法能解析的文法，都是後一個的真子集。

Calc文法一鍵生成解析器相關的資料，可見於（https://www.cnblogs.com/bitzhuwei/p/Calc-readme-full.html）。

語意分析器

前文提過，如果按後序優先遍歷的方式過一遍語法樹，就可以得到依索引排列的TokenList。我們想知道46*(87-19)的算術結果是多少，這可以通過按後序優先遍歷的順序對各個V分別執行相應的操作來實現。相應的操作，反映到程式碼上，就是針對每種V都設計一個delegate。

每個Vt的操作都是一樣的：將它的Token入棧，供上級使用。

private static readonly Action<Node, TContext<FinalValue>> VtHandler =
    (node, context) => {
        var token = context.tokens[node.tokenIndex];
        context.objStack.Push(token);
    };

對Multiplicative : Multiplicative '*' Primary這個Regulation來說，棧裡會有3個物件，分別出棧，執行乘法計算，將結果入棧即可。其它Vn的思路相同，不再重述。

    // 3: Multiplicative : Multiplicative '*' Primary ;
    var primary0 = context.objStack.Pop() as Primary;
    var asterisk1 = context.objStack.Pop() as Token;
    var multiplicative2 = context.objStack.Pop() as Multiplicative;
    var multiplicative = new Multiplicative(multiplicative2.value * primary0.value);
    context.objStack.Push(multiplicative);

後序優先遍歷的遞迴版如下：

    public void PostOrderRecursion(Node node)
    {
        for (int i = 0; i < node.Children.Count; i++)
        {
            PostOrderRecursion(node.Children[i]);
        }

        Visit(node);
    }

    private void Visit(Node node) {
        // do something.
    }

後序優先遍歷的非遞迴版如下：

    public void PostOrder(Node rootNode) {
        // post-order traverse rootNode with stack(without recursion).
        var nodeStack = new Stack<Node>();
        var indexStack = new Stack<int>();
        // init stack.
        {
            // push nextLeft and its next pending children.
            var nextLeft = rootNode;
            nodeStack.Push(nextLeft); indexStack.Push(0);
            while (nextLeft.Children.Count > 0) {
                nextLeft = nextLeft.Children[0];
                nodeStack.Push(nextLeft);
                indexStack.Push(0);
            }
        }

        while (nodeStack.Count > 0) {
            var current = nodeStack.Pop();
            var index = indexStack.Pop() + 1;
            if (index < current.Children.Count) {
                // push this node back again.
                nodeStack.Push(current); indexStack.Push(index);

                // push nextLeft and its next pending children.
                var nextLeft = current.Children[index];
                nodeStack.Push(nextLeft); indexStack.Push(0);
                while (nextLeft.Children.Count > 0) {
                    nextLeft = nextLeft.Children[0];
                    nodeStack.Push(nextLeft);
                    indexStack.Push(0);
                }
            }
            else {
                Visit(current);
            }
        }
    }

    private void Visit(Node node) {
        // do something.
    }

其它

手工編寫詞法分析器和語法分析器是簡單而枯燥的。如果文法比較複雜，那麼工作量也會大增，很容易寫錯。下面我們來實現解析器的一鍵生成功能。

讀者可以預先看看Calc一鍵生成的各種資料結構（nullable、FIRST、FOLLOW、詞法分析表、語法分析表等）（https://www.cnblogs.com/bitzhuwei/p/Calc-readme-full.html）。

進入正題——文法解析器`CompilerGrammar`

讀者可在下述連結（https://www.cnblogs.com/bitzhuwei/p/some-grammars.html）中找到一些文法的例子。

經過一些練習，我們可以用文法來描述文法：

// GrammarName = Grammar
// ExtractedType = GrammarDraft
StatementList : StatementList Statement | Statement ;
Statement : SyntaxProduction | LexiProduction ;
SyntaxProduction : 'Vn' ':' CandidateList ';' ;
CandidateList : CandidateList '|' Candidate | Candidate ;
Candidate : VList | 'empty' ;
VList : VList V | V ;
V : 'Vn' | 'Vt' ;
LexiProduction : 'Vt' ':' 'pattern' ';' ;
// 3 VtPatterns:
'Vn' : %%[a-zA-Z_][a-zA-Z0-9_]*%% ;
'Vt' : %%'([ -&]|\\'|[(-\[]|\\\\|[\]-~])+'%% ;
'pattern' : %%[%]{2}[ -~]([^%]|%[^%])*[%]{2}%% ;

我們可以照葫蘆畫瓢，藉助寫CompilerCalc的經驗，得到Grammar的資料結構GrammarDraft。對GrammarDraft進行一系列演演算法操作，就可以得到任意文法的解析器了。

一鍵生成詞法分析器

詞法分析器，需要生成的是自動機對應的程式碼。自動機在文法中是用%%xxx%%裡的正規表示式描述的。我們要做的，就是把string格式的正規表示式，轉化為Automaton資料結構，最後轉化為C#程式碼。

正規表示式也是一門程式語言，應當用文法描述和解析。這裡需要解析的正規表示式格式如下：

// something(xxx) between %%xxx%%
// GrammarName=Pattern
// ExtractedType=TokenDraft
// VnRegulations:
Pattern    : PreRegex Regex PostRegex ;
PreRegex   : 'refVt' | empty ;
PostRegex  : '/' Regex | empty ;
Regex      : Regex '|' Bunch | Bunch;
Bunch      : Bunch Unit | Unit ;
Unit       : 'char' Repeat | '.' Repeat | 'scope' Repeat | '(' Regex ')' Repeat ;
Repeat     : '?' | '+' | '*' | '{' 'min' UpperBound '}' | empty ;
UpperBound : ',' 'max' | ',' | empty ;
// VtRegex:
'refVt'    : %%\<'([ -&]|\\'|[(-\[]|\\\\|[\]-~])+'\>%% ; // start with <' and end with '> 
'min'      : %%<'{'>[0-9]+%% ;
'max'      : %%<','>[0-9]+%% ;
// 'char' is a letter or an escape
'char'     : %%[ !"#%&',]|-|[0-9:;<=>@A-Z_`a-z~]|\\[$()*+]|\\-|\\[./<>?]|\\\[|\\\\|\\\]|\\\^|\\\{|\\\||\\\}|\\u[0-9a-fA-F]{4}%% ;
//'scope'    : %%\[((firstLetter1)(char)*|\^(firstLetter2)(char)*)\]%% ; // a-z or A-Z or ...
//firstLetter1 = \\u[0-9]{4}|\\t|\\n|\\r|\\-|[ -Z]|\[|\\\\|]|\\\^|[_-~]
//firstLetter2 = \\u[0-9]{4}|\\t|\\n|\\r|\\-|[ -Z]|\[|\\\\|]|\^|\\\^|[_-~]
//char =         \\u[0-9]{4}|\\t|\\n|\\r|\\-|[ -Z]|\\\[|\\\\|\\\]|\^|\\\^|[_-~]
'scope'    : %%\[((\\u[0-9]{4}|\\t|\\n|\\r|\\-|[ -Z]|\[|\\\\|]|\\\^|[_-~])(\\u[0-9]{4}|\\t|\\n|\\r|\\-|[ -Z]|\\\[|\\\\|\\\]|\^|\\\^|[_-~])*|\^(\\u[0-9]{4}|\\t|\\n|\\r|\\-|[ -Z]|\[|\\\\|]|\^|\\\^|[_-~])(\\u[0-9]{4}|\\t|\\n|\\r|\\-|[ -Z]|\\\[|\\\\|\\\]|\^|\\\^|[_-~])*)\]%% ; // a-z or A-Z or ...

這個文法看起來嚇人，實際上用手工實現也不困難，只是需要耐心和細心。

Lex用字首和字尾增強了描述自動機的能力，它使用的已經不是純粹的正規表示式（regex）了，而是<'xxx'>regex/post-regex。因此，我將此文法稱為Pattern而不是Regex。我認為這個增強的功能很有必要，且其實現並不特別困難，所以這裡也實現了它。

字首<'xxx'>

字首能起到這樣的作用：在識別了一個'xxx'型別的Token後，應當將後續的regex認定為某個型別。

例如，'min' : %%<'{'>[0-9]+%% ;的意思是，在識別了一個'{'後，應當將後續的數值認定為一個'min'。而'max' : %%<','>[0-9]+%% ;的意思是，在識別了一個','後，應當將後續的數值認定為一個'max'。這樣，同樣的內容就能夠在不同的字首下被認定為不同的型別了。這大大有利於後續的語法分析。

此功能的實現，就是將[0-9]+的自動機的開頭連結到'{'或','的自動機的末尾。

字尾/post-regex

字尾能起到這樣的作用：在識別了一個post-regex之後，才將'/'前面的regex認定為某個型別。

例如，下述文法：

Item : 'entityId' '=' 'refEntity' ;
'entityId' : %%[A-Za-z_][A-Za-z0-9_]*/=%% ;
'refEntity' : %%[A-Za-z_][A-Za-z0-9_]*%% ;

只有識別了一個'='的時候，才會將前面的識別符號認定為'entityId'。也就是說，像平時一樣記錄Token的起始位置和長度，但直到讀到了'='才設定Token的型別。

此功能的實現，就是將post-regex（/後面的regex）連結到regex末尾。

從string到Automaton，需要經歷string => ε-NFA => NFA => DFA => MiniDFA的過程。

ε-NFA

為了連結regex內部和外部各種結構，我們先用空ε邊把它們連結起來。空ε邊就是不需要讀入任何char就可以跳轉過去的邊。有空ε邊的自動機，我們稱為ε-NFA。

Calc文法的ε-NFA如下圖所示：

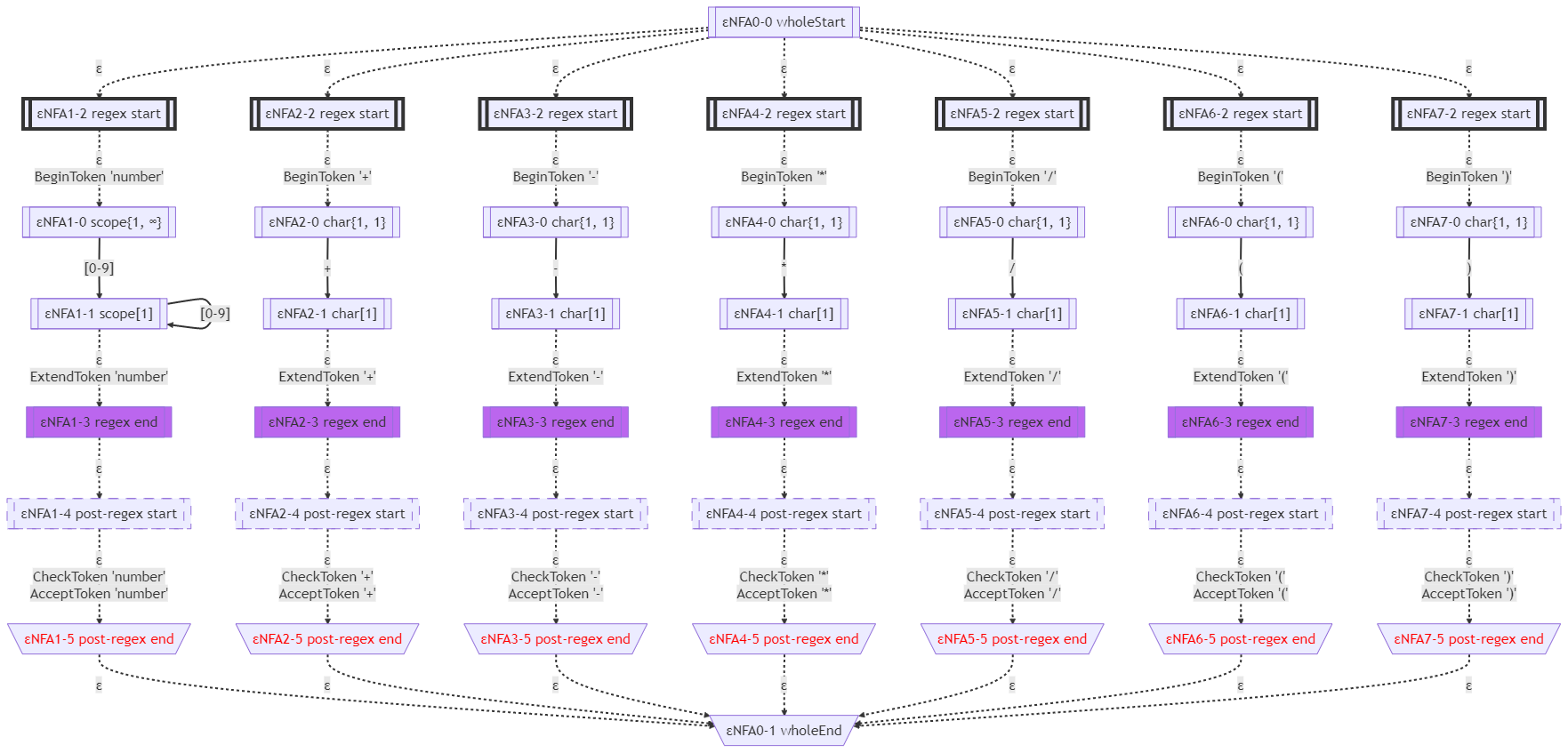
NFA

現在，我們設法去掉空ε邊，也就是將ε-NFA轉換為NFA。

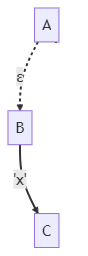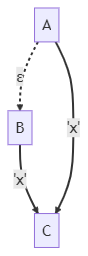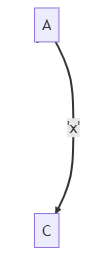
演演算法思想如下：如上圖所示，A可以通過空ε邊到達B，B可以通過'x'到達C。這說明，A也可以通過'x'到達C。也就是說，隱含著一條A-'x'->C的邊。

我們將此邊建立起來，使它不再隱式存在，而是顯式存在。

這樣，就不需要繼續保持原來的空ε邊了。因為空ε邊的意義，就是隱式的表明A-'x'->C邊的存在，再無其他。

為了去掉空ε邊，我們只需遍歷此圖的各個結點N，當從N走出去的邊為空ε邊時，直接忽略它，不去遍歷它指向的結點。這樣，將全部被遍歷到的結點及其非空ε邊收集起來，就是不含空ε邊的NFA了。

將Calc文法的ε-NFA隱含的邊都顯示出來，如下圖所示：

將Calc文法的ε-NFA的空ε邊都去掉，得到的NFA如下圖所示：

DFA

如果既需要識別整數[0-9]+，又需要識別浮點數[0-9]+[.][0-9]+，那麼當詞法分析器讀入的char是[0-9]中的一個時，就無法判斷接下來會遇到的是什麼型別的Token了，這怎麼辦？

理論化的說，如果一個自動機裡的狀態A，存在A-'x'->C和A-'x'->D這樣的兩個邊，那麼，狀態A讀到'x'時，就不知道該跳轉到狀態C還是狀態D了。

將NFA轉化為DFA，就是為了去掉這樣的邊。不含這樣的邊的NFA，就成了DFA。這個過程被稱為確定化。

演演算法（子集法）思想如下：

假設，狀態A，存在A-'x'->C和A-'x'->D這樣的兩個邊。那好，狀態A構成一個新狀態X{A}，狀態C和狀態D合起來構成一個新狀態Y{C,D}，X{A}-'x'->Y{C,D}。我們可以說狀態C和狀態D組成了一個小家庭，住進了它們的小房子Y{C,D}，它們共用一切；狀態A是單身漢，自己住一套小房子X{A}。狀態C和狀態D的任何邊，都是Y{C,D}的邊，都是這個小家庭的邊。狀態A的任何邊，都是X{A}的邊，都是這個獨居戶的邊。
繼續假設，狀態A，存在A-'t'->D和A-'t'->E這樣的兩個邊。類似上一步，狀態A組成新狀態X{A}，狀態D和狀態E合起來構成一個新狀態Z{D,E}，X{A}-'t'->Z{D,E}。我們可以說狀態D和狀態E組成了一個小家庭，住進了它們的小房子Z{D,E}，它們共用一切；狀態A是單身漢，自己住一套小房子X{A}。狀態D和狀態E的任何邊，都是Z{D,E}的邊，都是這個小家庭的邊。狀態A的任何邊，都是X{A}的邊，都是這個獨居戶的邊。
注意，狀態D同時參與了小房子Y{C,D}和小房子Z{D,E}的構建，它腳踏兩隻船。在人間，這是被批判的；在自動機，這是很普遍的，而且是可以腳踏好多船的。
全部小房子就是DFA的狀態，小房子之間的邊就是DFA狀態的邊。

一個小房子裡，任何一個NFA狀態都可能住進去，也可能不住進去，僅此兩種可能。如果NFA有10個狀態，那麼，可能的小家庭就有2^10-1=1023種（10個人都不住進去，就空了）。這說明，從有n個狀態的NFA轉換為DFA，此DFA最多可能有2^n-1個狀態。

Calc文法的DFA如下圖所示：

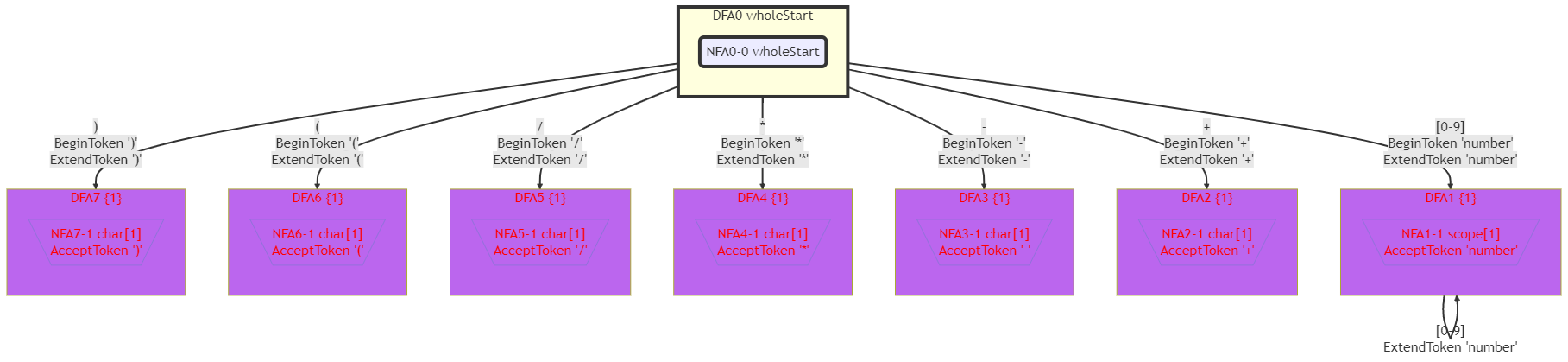
可見，每個DFA小房子裡都只有1個NFA。如果不如此詳細地繪製包含的NFA，那麼DFA如下圖所示：

如果每個DFA小房子裡都只有1個NFA，說明那個NFA本身就已經是DFA了。

為了直觀展示NFA與DFA的區別，這裡再舉一個文法的例子：

// GrammarName = Scope
// ExtractedType = ResolvedScope
Scope : '[' 'firstItem1' RangeItems ']' ;
Scope : '[^' 'firstItem2' RangeItems ']' ;
Scope : '[' 'firstItem1' ']' ;
Scope : '[^' 'firstItem2' ']' ;
RangeItems : RangeItems RangeItem | RangeItem ;
RangeItem : 'char' ;

// \uNNNN \t \n \r 口 ! " # $ % & '
// ( ) * + , - . /
// 0 1 2 3 4 5 6 7 8 9
// : ; < = > ? @
// A B C D E F G H I J K L M
// N O P Q R S T U V W X Y Z
// [ \ ] ^ _ `
// a b c d e f g h i j k l m
// n o p q r s t u v w x y z
// { | } ~

// escape: \ ^
'firstItem1' : %%<'['>\\u[0-9]{4}|\\t|\\n|\\r|\\-|[ -Z]|\[|\\\\|]|\\\^|[_-~]%% ;
// escape: \
'firstItem2' : %%<'[^'>\\u[0-9]{4}|\\t|\\n|\\r|\\-|[ -Z]|\[|\\\\|]|\^|\\\^|[_-~]%% ;
// escape: [ \ ]
'char' : %%\\u[0-9]{4}|\\t|\\n|\\r|\\-|[ -Z]|\\\[|\\\\|\\\]|\^|\\\^|[_-~]%% ;

這個Scope文法，是為了解析正規表示式中的[xxx]結構而作的。當然，我們可以把這個文法融入Pattern文法中，還可以再把Pattern文法融入Grammar文法中。但那樣的文法太龐大，不易維護。

讀者可以在（https://www.cnblogs.com/bitzhuwei/p/Scope-readme-full.html）瀏覽直接用Mermaid展示的詳情。

這個Scope文法的ε-NFA如下圖所示：

由於顯式的ε-NFA太龐大，Mermaid渲染器拒絕了渲染：

這個Scope文法的NFA如下圖所示：

這個Scope文法的DFA如下圖所示：

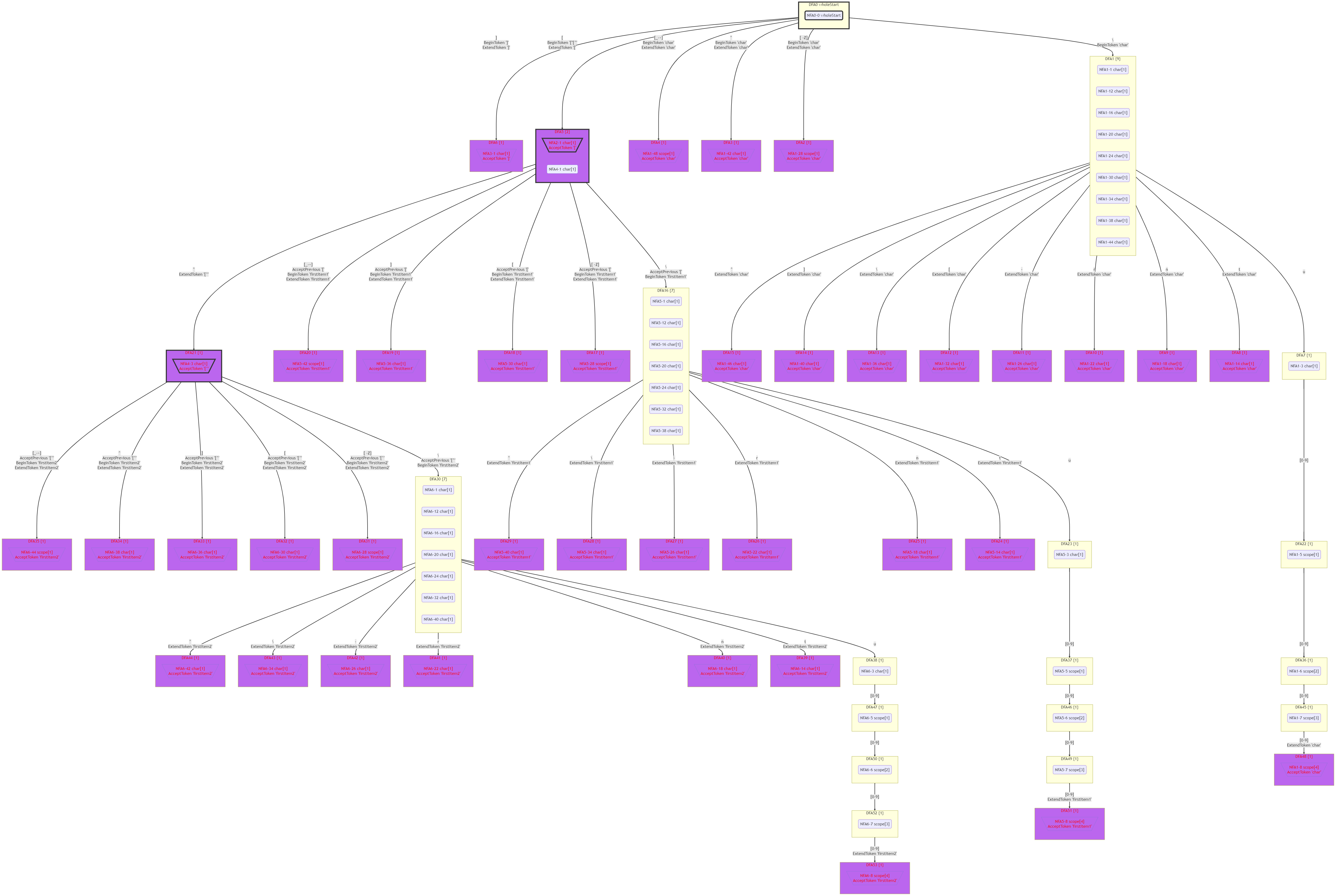
可見，有的DFA小房子裡包含多個NFA狀態。會出現這種情況，是因為存在[和[^這樣的含有相同的開頭的Token型別。可惜這個例子裡沒有出現腳踏兩隻船的情況。

這個Scope文法的DFA（簡化顯示）如下圖所示：

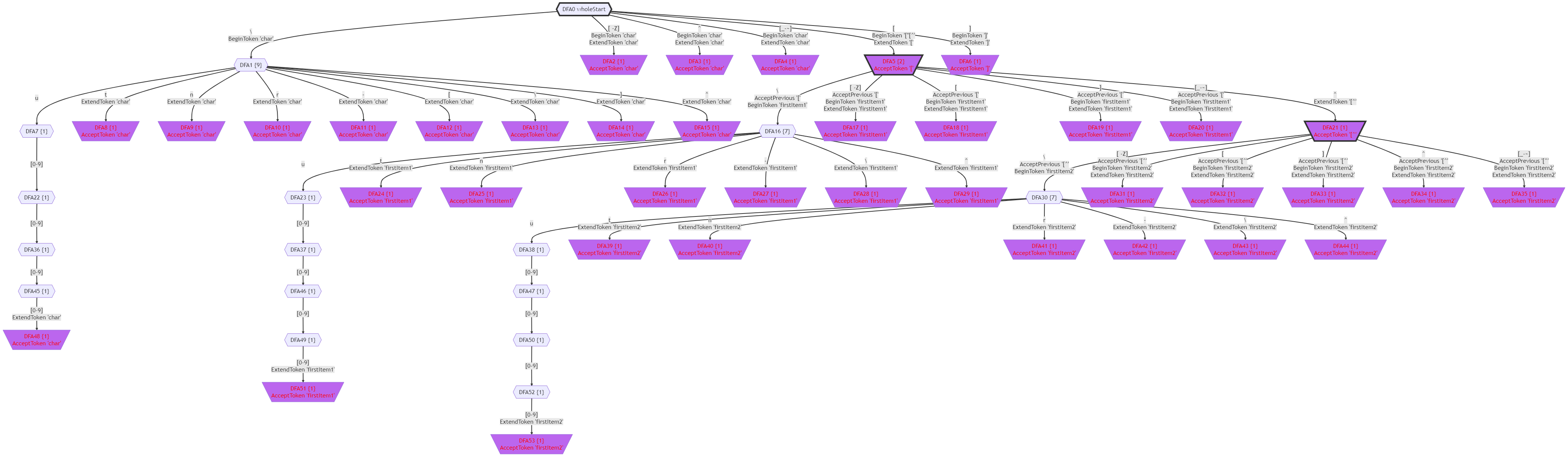
下面這個文法的DFA裡出現了腳踏兩隻船的情況：

// 1 VnRegulations:
PreRegex : 'refVt' ; // [0]
// 1 VtPatterns:
'refVt' : %%(\\|[Y-\\])+%% ; // [0]

這個文法實際上是Pattern的一小部分，當時的'refVt'我寫錯了，卻恰好見到了腳踏兩隻船的情況。

這個文法的ε-NFA如下圖所示：

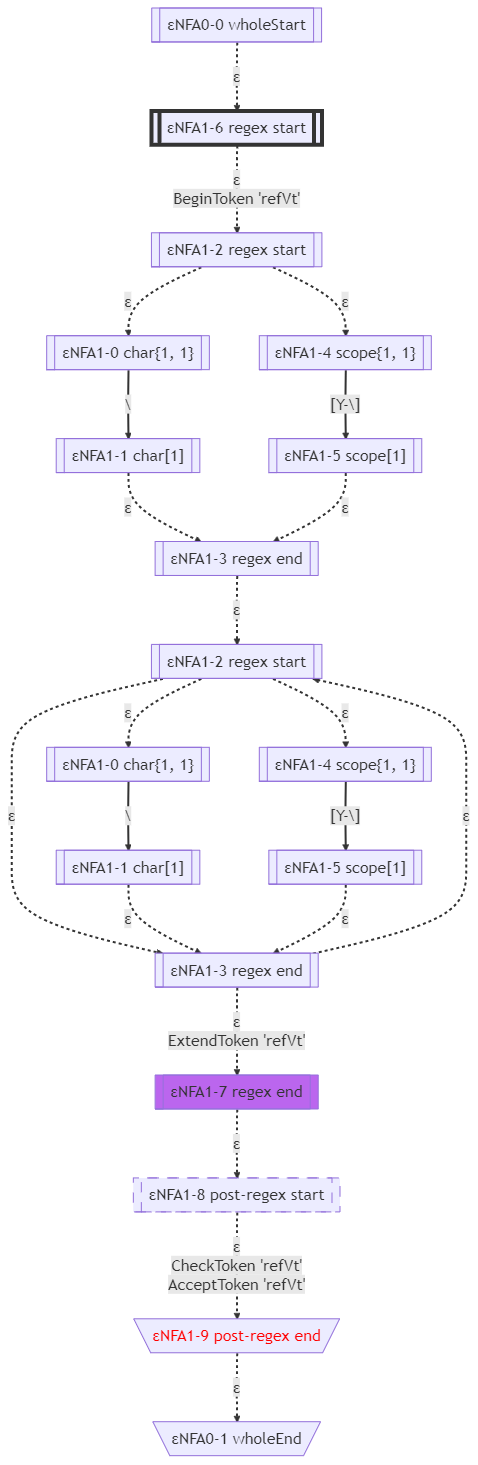
這個文法的顯式的ε-NFA如下圖所示：

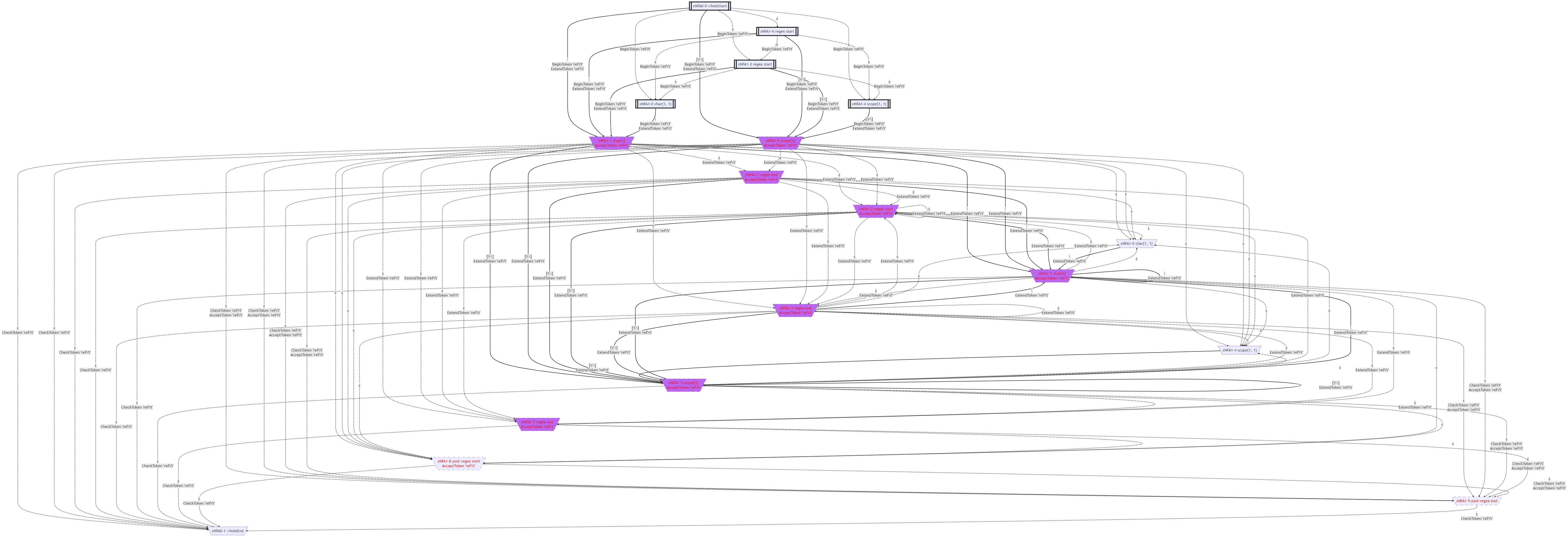
這個文法的NFA如下圖所示：

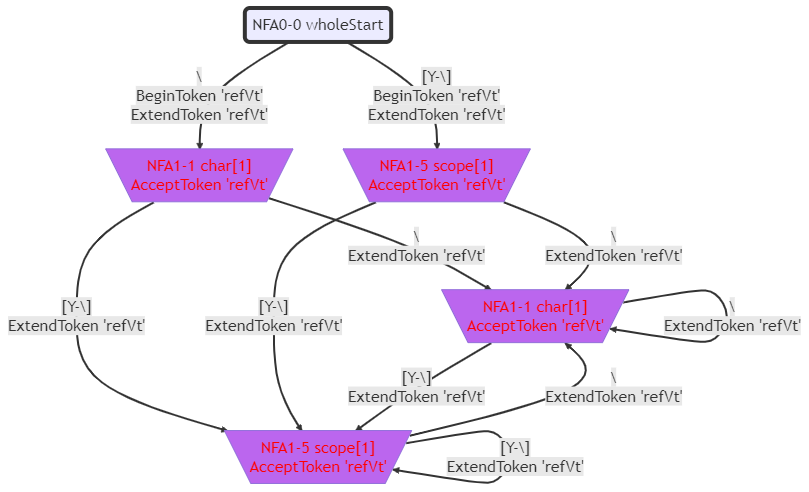
這個文法的DFA如下圖所示：

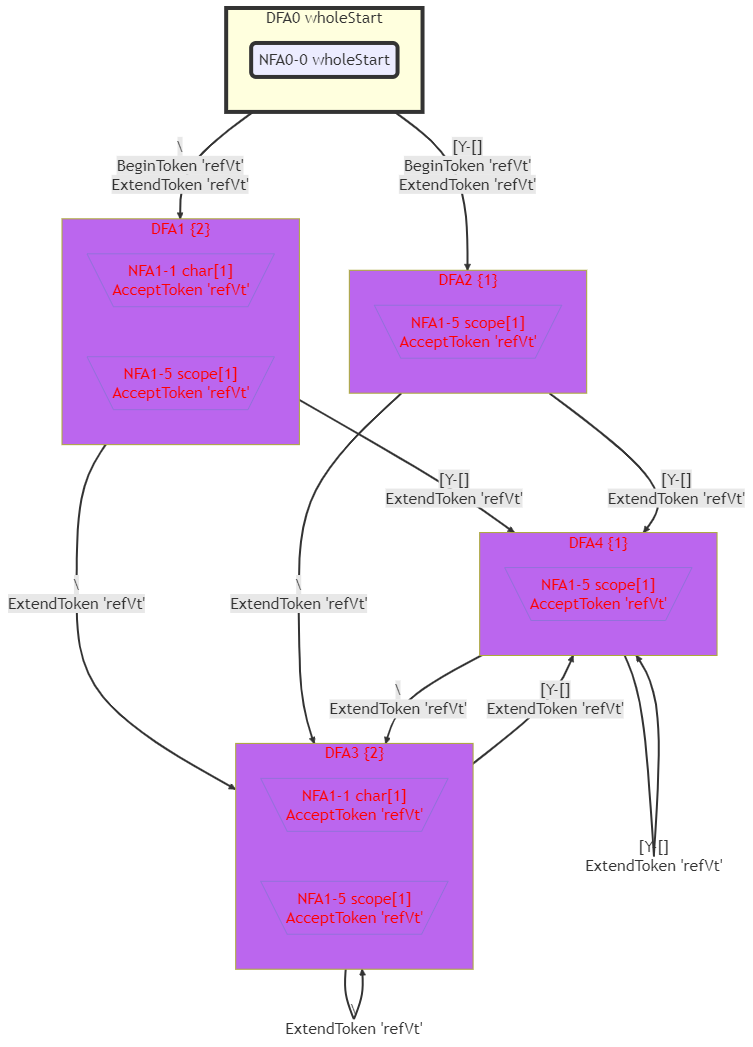
MiniDFA

有了DFA，就可以將其轉換為C#程式碼了。但DFA還有減少狀態的可能。將DFA的狀態減至最少，它轉換出的C#程式碼也會佔用更少的記憶體，有利於提升效率。這種可能的最少狀態的DFA，我們稱為MiniDFA。

演演算法（Hopcroft）思想如下：

將終態放到同一個小房子（集合），非終態放到另一個小房子（集合）。哪些是終態呢？能夠認定一個Token的狀態，就是終態，否則就是非終態。
同一個小房子裡的DFA狀態A和DFA狀態B，如果它們在經過某個'x'時，DFA狀態A指向了一個小房子，DFA狀態B指向了另一個小房子，就說明它們不等價，它們應當被放到不同的小房子裡；如果它們在經過ASCII碼中每一個char時，指向的小房子都相同，就說明它們等價，它們應當被放到相同的小房子裡。例如，如果它們在經過'\0'-'P'這些char時，都指向小房子M；它們在經過'Q'-'~'這些char時，都指向小房子N，就說明它們等價。
所有的小房子構成MiniDFA狀態，小房子中各個DFA狀態之間的邊就是MiniDFA狀態的邊。

MiniDFA的小房子與DFA的小房子不同：一個DFA狀態，只會住進一個MiniDFA的小房子裡，不會出現腳踩兩隻船的情況。

Calc文法的MiniDFA如下圖所示：

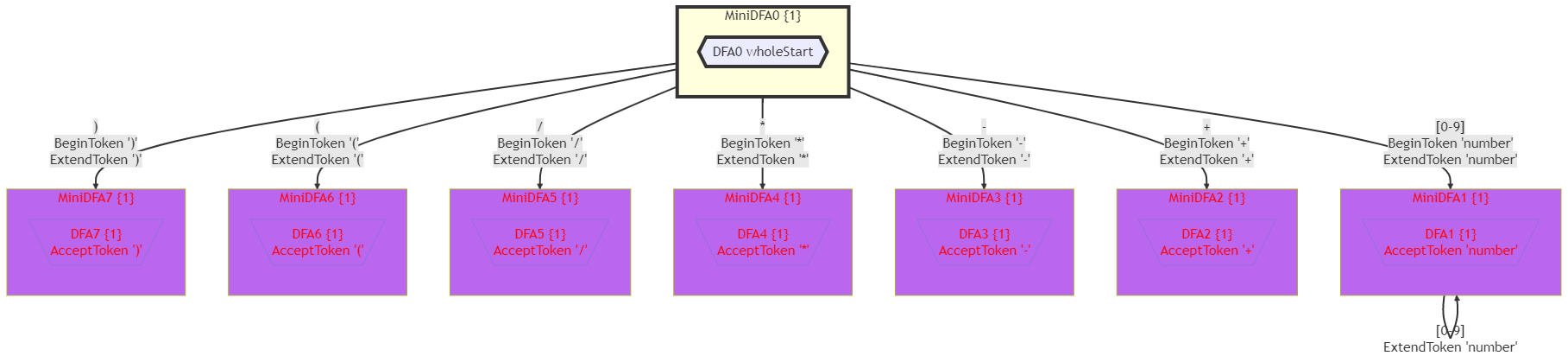
如果不詳細地顯示包含的DFA，那麼MiniDFA如下圖所示：

MiniDFA在Calc文法中沒有顯示出明顯的作用。在Pattern文法中，它能夠將詞法分析器狀態從611個DFA狀態降低到86個MiniDFA狀態。

一鍵生成語法分析器

上文運用LL(1)、LR(0)、SLR(1)、LALR(1)、LR(1)分析法的過程，就是手工執行演演算法的過程。將此過程整理成程式碼，就是一鍵生成語法分析器的功能。

計算nullable(VList)

演演算法思想：

全部Vt都是不可空的，即nullable(Vt)=false。
先假設全部Vn也都是不可空的，即nullable(Vn)=false。
如果有Vn : empty ;這樣的Regulation，那麼nullable(Vn)=true。
對於Vn : V1 V2 V3 .. ;這樣的Regulation，如果nullable(V1 V2 V3 ..)=true，那麼nullable(Vn)=true。
迭代到不動點。

public static Dictionary<string, bool> GetNullableDict(this VnRegulationDraft[] vnRegulations) {
    var nullableDict = new Dictionary<string/*Node.type*/, bool>();

    // allocate space for all kinds of nodes(Vt and Vn, no empty).
    var allNodeTypes = vnRegulations.GetNodes();
    foreach (var item in allNodeTypes) {
        nullableDict.Add(item, false);
    }

    nullableDict.Add(string.Empty, true);

    // iterate untill not changed.
    bool changed = false;
    do {
        changed = false;
        foreach (var regulation in vnRegulations) {
            // 如果regulation.right可推匯出empty，就說明regulation.left可推匯出empty。
            // if regulation.right can refer to 'empty',
            // then regulation.left, too.
            if (CanBeEmpty(regulation.Right, nullableDict)) {
                var left = regulation.left;
                if (!nullableDict[left]) {
                    nullableDict[left] = true;
                    changed = true;
                }
            }
        }
    } while (changed);

    return nullableDict;
}

計算FIRST(VList)

演演算法思想：

對於全部Vt都有：FIRST(Vt)={ Vt }。
對於全部Vn都有：若nullable(Vn)=true，則FIRST(Vn)包含空ε。
對於Vn : V1 V2 V3 .. ;這樣的Regulation：FIRST(Vn)包含FIRST(V1)；若nullable(V1)=true，則FIRST(Vn)還包含FIRST(V2)；若nullable(V1 V2)=true，則FIRST(Vn)還包含FIRST(V3)；以此類推。
迭代到不動點。

private static Dictionary<string, FIRST> GetFIRSTDict4Node(this VnRegulationDraft[] regulations, Dictionary<string, bool> nullableDict) {
    var result = new Dictionary<string/*V*/, FIRST>();
    var empty = "empty"; /* ε */
    // allocate space for all single nodes.
    // 初始化FIRST(Vn)
    foreach (var Vn in regulations.GetVnNodes()) {
        if (nullableDict[Vn]) {
            var first = new FIRST(Vn, empty);
            result.Add(Vn, first);
        }
        else {
            var first = new FIRST(Vn);
            result.Add(Vn, first);
        }
    }

    // 初始化FIRST(Vt)（FIRST(Vt)實際上已經完工）
    foreach (var Vt in regulations.GetVtNodes()) {
        var first = new FIRST(Vt, Vt);
        result.Add(Vt, first);
    }

    bool changed = false;
    do {
        changed = false;
        foreach (var regulation in regulations) {
            var left = regulation.left; var right = regulation.Right;
            // try to collect FIRST( left )
            for (int checkpoint = 0; checkpoint < right.Count; checkpoint ++) {
                // 如果前checkpoint個結點都可為null，
                // 就說明 FIRST(left) 包含 FIRST(right[checkpoint])，empty除外。
                // if regulation.right[(-1)->(checkpoint-1)] can be empty,
                // then FIRST( left ) includes FIRST( right[checkpoint] )
                // except for empty.
                if (CanBeEmpty(right, 0, checkpoint, nullableDict)) {
                    var refKey = right[checkpoint];
                    if (left != refKey) {
                        if (!result.TryGetValue(left, out FIRST first)) { throw new Exception(algorithmError); }
                        if (!result.TryGetValue(refKey, out FIRST refFirst)) { throw new Exception(algorithmError); }
                        foreach (var value in refFirst.Values) {
                            if (value != empty) {
                                changed = first.TryInsert(value) || changed;
                            }
                        }
                    }
                }
            }
            {
                // if regulation.right can be empty,
                // then regulation.left can be empty.
                if (CanBeEmpty(right, nullableDict)) {
                    if (!result.TryGetValue(left, out FIRST first)) { throw new Exception(algorithmError); }
                    changed = first.TryInsert(empty) || changed;
                }
            }
        }
    } while (changed);
}

計算FOLLOW(Vn)

演演算法思想：

對於left : 某V 某V .. Vn V1 V2 .. ;這樣的Regulation：

FOLLOW(Vn)包含FIRST(V1)；

若nullable(V1)=true，則FOLLOW(Vn)還包含FIRST(V2)；以此類推；

若nullable(V1 V2 ..)=true，則FOLLOW(Vn)還包含FOLLOW(left)。
迭代到不動點。

public static Dictionary<string/*FOLLOW.target*/, FOLLOW> GetFOLLOWDict(this VnRegulationDraft[] regulations,
    Dictionary<string, bool> nullableDict, Dictionary<string, FIRST> firstDict) {
    var result = new Dictionary<string/*FOLLOW.Vn*/, FOLLOW>();

    // 初始化Follow Dict
    // allocate space for the FOLLOW( Vn ) items.
    foreach (var item in regulations.GetVnNodes()) {
        var follow = new FOLLOW(item);
        result.Add(follow.Vn, follow);
    }

    // 迭代到不動點
    // iterate untill not changed.
    bool changed = false;
    do {
        changed = false;
        foreach (var regulation in regulations) {
            var right = regulation.Right; int count = right.Count;
            for (int checkpoint = 0; checkpoint < count; checkpoint++) {
                string/*Node.type*/ target = right[checkpoint];
                if (target.IsVt()) { continue; } // 葉結點沒有FOLLOW

                // 準備為target新增follow元素
                // try to collect FOLLOW( target )
                var checkIndex = checkpoint + 1;
                for (int checkCount = 0; checkCount < count - checkIndex; checkCount++) {
                    // if right[checkIndex->(checkIndex+checkCount-1)] can be empty,
                    // then FOLLOW( target ) includes FIRST( right[checkInde+checkCount] )
                    // except empty.
                    if (CanBeEmpty(right, checkIndex, checkCount, nullableDict)) {
                        // FOLLOW( target ) 包含 FIRST( right[checkInde+checkCount] )（除了empty）
                        var Vn = target;
                        if (!result.TryGetValue(Vn, out FOLLOW follow)) { throw new Exception(algorithmError); }
                        string key = right[checkIndex + checkCount];
                        if (!firstDict.TryGetValue(key, out FIRST first)) { throw new Exception(algorithmError); }
                        foreach (var value in first.Values) {
                            if (value != "empty") {
                                changed = follow.TryInsert(value) || changed;
                            }
                        }
                    }
                }
                {
                    var checkCount = count - checkIndex;
                    // 如果target之後的全部結點都可為empty，那麼 FOLLOW( target ) 包含 FOLLOW( regulation.left )
                    // if right[checkIndex->(count - checkIndex-1)] can be empty,
                    // then FOLLOW( target ) includes FOLLOW( regulation.left ).
                    if (CanBeEmpty(right, checkIndex, checkCount, nullableDict)) {
                        if (!result.TryGetValue(target, out FOLLOW follow)) { throw new Exception(algorithmError); }
                        if (!result.TryGetValue(regulation.left, out FOLLOW refFollow)) { throw new Exception(algorithmError); }
                        if (follow != refFollow) {
                            foreach (var item in refFollow.Values) {
                                changed = follow.TryInsert(item) || changed;
                            }
                        }
                    }
                }

            }
        }
    } while (changed);

    return result;
}

擴充套件文法

這是一個程式設計技巧：對任何文法，都在開頭新增一個S2結點，作為初始結點。這樣可以使得完成動作只存在1個。我將擴充套件的文法稱為eGrammar，其產生式部分稱為eRegulations，（e代表extended）額外新增的這個Regulation稱為擴充套件Regulation。

例如，擴充套件的四則運算Calc文法如下：

// GrammarName = Calc
// ExtractedType = FinalValue
S2             : Additive ;
Additive       : Additive '+' Multiplicative // R[0]
               | Additive '-' Multiplicative // R[1]
               | Multiplicative ; // R[2]
Multiplicative : Multiplicative '*' Primary // R[3]
               | Multiplicative '/' Primary // R[4]
               | Primary ; // R[5]
Primary        : '(' Additive ')' // R[6]
               | 'number' ; // R[7]
// 用 %%xxx%% 格式 描述單詞
'number'       : %%[0-9]+%% ; // 為便於演示，僅處理正整數

LL(1)分析法

演演算法思想：

對於Vn : V1 V2 V3 .. ;這樣的Regulation：

對於FIRST(V1 V2 V3 ..)中的每個元素Vt（不含空ε），在LL(1)分析表中記錄下「Vn行Vt列對應Vn : V1 V2 V3 .. ;」，意為「在Vn狀態下遇到Vt時，應當使用Vn : V1 V2 V3 .. ;進行規約」；

若FIRST(V1 V2 V3 ..)包含空ε，則在LL(1)分析表中記錄下「Vn行全部FOLLOW(Vn)列對應Vn : V1 V2 V3 .. ;」，意為「在Vn狀態下遇到Vt時，應當使用Vn : V1 V2 V3 .. ;進行規約」。

public static LL1SyntaxInfo GetLL1SyntaxInfo(this VnRegulationDraft[] regulations,
    VnRegulationDraft[] eRegulations,
    Dictionary<string, FOLLOW> eFOLLOWDict, Dictionary<string, FIRST> eFIRSTDict) {
    var regCount = regulations.Length;
    var table = new LL1ParsingTableDraft();
    for (int regulationId = 0; regulationId < regulations.Length; regulationId++) {
        var regulation = regulations[regulationId];
        var Vn = regulation.left;
        var key = FIRST.MakeKey(regulation.Right);
        var first = eFIRSTDict[key]; // FIRST( regulation.Right )
        var firstCount = first.Values.Count;
        for (int index = 0; index < firstCount; index++) {
            var VtOrEmpty = first.Values[index];
            if (VtOrEmpty != "empty" /* ε */) {
                table.SetAction(Vn, VtOrEmpty, new LL1ParsingActionDraft(regulationId));
            }
            else {
                var follow = eFOLLOWDict[Vn];
                foreach (var Vt in follow.Values) {
                    table.SetAction(Vn, Vt, new LL1ParsingActionDraft(regulationId));
                }
            }
        }
    }

    var result = new LL1SyntaxInfo(table);

    return result;
}

LR(0)分析法

演演算法思想：

拿到第一個Regulation（Vn:V1 V2 V3 .. ;），以 Vn: ⏳ V1 V2 V3 .. ;為初始LR(0)狀態，並求解其閉包。實際上，第一個Regulation就是擴充套件Regulation。
對每個LR(0)狀態A，讓⏳向前移動一個V，得到下一個LR(0)狀態B，並求解其閉包。
將A-V->B設定為LR(0)邊。
設定LR(0)分析表：對每個LR(0)邊（例如A-V->B），若V是Vt，則在A行V列記錄移進到B；若V是Vn，則在A行V列記錄跳入B。
設定LR(0)分析表：對每個LR(0)狀態（例如A）中的每個Item，若Item中的⏳位於Regulation末尾，一般情況下，則在A行全部Vt列（包括'¥'列）記錄用Regulation規約；特殊情況（Regulation是擴充套件Regulation）下，則在A行'¥'列記錄完成。

public static LR0SyntaxInfo GetLR0SyntaxInfo(this VnRegulationDraft[] regulations,
    VnRegulationDraft[] eRegulations) {
    var stateList = new LR0StateList();
    var edgeList = new LR0EdgeList();
    var queue = new Queue<LR0State>(); {
        var firstItem = LR0Item.GetItem(eRegulations[0], 0);
        var firstState = new LR0State(firstItem); Closure(firstState, eRegulations);
        stateList.TryInsert(firstState);
        queue.Enqueue(firstState);
    }
    while (queue.Count > 0) {
        var from = queue.Dequeue();
        foreach (var item in from.Items) {
            string/*Node.type*/ V = item.nodeNext2Dot;
            if (V == null) { continue; }

            var to = Goto(from, V); Closure(to, eRegulations);
            if (stateList.TryInsert(to)) { // to是新狀態
                queue.Enqueue(to);
                var edge = new LR0Edge(from, V, to);
                edgeList.TryInsert(edge);
            }
            else { // to是已有狀態
                int t = stateList.IndexOf(to);
                var oldTo = stateList.States[t];
                var edge = new LR0Edge(from, V, to);
                edgeList.TryInsert(edge);
            }
        }
    }
    
    var table = new LRParsingTableDraft();
    foreach (var edge in edgeList.Edges) {
        if (edge.V.IsVt()) {
            // shift in action
            table.SetAction(edge.from.index, edge.V, new LRShiftInActionDraft(edge.to.index));
        }
        else { // V is Vn
            // goto action
            table.SetAction(edge.from.index, edge.V, new LRGotoActionDraft(edge.to.index));
        }
    }
    var Vts = eRegulations.GetVtNodes();
    var eLeft = eRegulations[0].left; // the S' in many books.
    var eEnd = '¥'; // similar to '\0' in lexical analyzing
    foreach (var state in stateList.States) {
        foreach (var item in state.Items) {
            string/*Node.type*/ V = item.nodeNext2Dot;
            if (V == null) {
                if (item.VnRegulation.left == eLeft) {
                    // accept action
                    var acceptAction = new LRAcceptActionDraft();
                    table.SetAction(state.index, eEnd, acceptAction);
                }
                else {
                    // reduction action
                    int reductionIndex = Array.IndexOf(eRegulations, item.VnRegulation) - 1;
                    var action = new LRReducitonActionDraft(reductionIndex);
                    foreach (var Vt in Vts) {
                        table.SetAction(state.index, Vt, action);
                    }
                    {
                        table.SetAction(state.index, eEnd, action);
                    }
                }
            }
        }
    }

    var result = new LR0SyntaxInfo(stateList, edgeList, table);

    return result;
}

LR(0)狀態求解閉包的演演算法：

對LR(0)狀態中的每個Item，若⏳後面的第一個V是Vn，則將所有的Vn : ⏳ V1 V2 V3 ..作為一個新的Item加入此狀態。
迭代至不再新增Item。

static void Closure(this LR0State state, VnRegulationDraft[] eRegulations) {
    var queue = new Queue<LR0Item>();
    foreach (var item in state.Items) { queue.Enqueue(item); }
    while (queue.Count > 0) {
        var item = queue.Dequeue();
        string/*Node.type*/ node = item.nodeNext2Dot;
        if (node == null || node.IsVt()) { continue; }

        foreach (var regulation in eRegulations) {
            if (regulation.left == node) {
                const int dotPosition = 0;
                var newItem = LR0Item.GetItem(regulation, dotPosition);
                if (state.TryInsert(newItem)) {
                    queue.Enqueue(newItem);
                }
            }
        }
    }
}

SLR(1)分析法

演演算法思想：

拿到第一個Regulation（Vn:V1 V2 V3 .. ;），以 Vn: ⏳ V1 V2 V3 .. ;為初始SLR(1)狀態，並求解其閉包。實際上，第一個Regulation就是擴充套件Regulation。
對每個SLR(1)狀態A，讓⏳向前移動一個V，得到下一個SLR(1)狀態B，並求解其閉包。
將A-V->B設定為SLR(1)邊。
設定SLR(1)分析表：對每個SLR(1)邊（例如A-V->B），若V是Vt，則在A行V列記錄移進到B；若V是Vn，則在A行V列記錄跳入B。
設定SLR(1)分析表：對每個SLR(1)狀態（例如A）中的每個Item，若Item中的⏳位於Regulation末尾，一般情況下，則在A行全部FOLLOW(Vn)列記錄用Regulation規約；特殊情況（Regulation是擴充套件Regulation）下，則在A行'¥'列記錄完成。

在記錄用Regulation規約方面，SLR(1)比LR(0)細膩，其他方面並無不同。

public static SLR1SyntaxInfo GetSLR1SyntaxInfo(this VnRegulationDraft[] regulations,
    VnRegulationDraft[] eRegulations, Dictionary<string, FOLLOW> eFOLLOWDict) {
    var stateList = new SLR1StateList();
    var edgeList = new SLR1EdgeList();
    var queue = new Queue<SLR1State>(); {
        var firstItem = SLR1Item.GetItem(eRegulations[0], 0);
        var firstState = new SLR1State(firstItem); Closure(firstState, eRegulations);
        stateList.TryInsert(firstState);
        queue.Enqueue(firstState);
    }
    while (queue.Count > 0) {
        var from = queue.Dequeue();
        foreach (var item in from.Items) {
            string/*Node.type*/ V = item.nodeNext2Dot;
            if (V == null) { continue; }

            var to = Goto(from, V); Closure(to, eRegulations);
            if (stateList.TryInsert(to)) { // to是新狀態
                queue.Enqueue(to);
                var edge = new SLR1Edge(from, V, to);
                edgeList.TryInsert(edge);
            }
            else { // to是已有狀態
                int t = stateList.IndexOf(to);
                var oldTo = stateList.States[t];
                var edge = new SLR1Edge(from, V, oldTo);
                edgeList.TryInsert(edge);
            }
        }
    }
    
    var table = new LRParsingTableDraft();
    foreach (var edge in edgeList.Edges) {
        if (edge.V.IsVt()) {
            // shift action
            table.SetAction(edge.from.index, edge.V, new LRShiftInActionDraft(edge.to.index));
        }
        else { // V is Vn
            // goto action
            table.SetAction(edge.from.index, edge.V, new LRGotoActionDraft(edge.to.index));
        }
    }
    var eLeft = eRegulations[0].left; // the S' in many books.
    var eEnd = '¥';
    foreach (var state in stateList.States) {
        foreach (var item in state.Items) {
            string/*Node.type*/ V = item.nodeNext2Dot;
            if (V == null) {
                if (item.VnRegulation.left == eLeft) {
                    // accept action
                    var action = new LRAcceptActionDraft();
                    table.SetAction(state.index, eEnd, action);
                }
                else {
                    // reduction action
                    int reductionIndex = Array.IndexOf(eRegulations, item.VnRegulation) - 1;
                    var action = new LRReducitonActionDraft(reductionIndex);
                    if (!eFOLLOWDict.TryGetValue(item.VnRegulation.left, out FOLLOW follow)) { throw new Exception(algorithmError); }
                    foreach (var Vt in follow.Values) {
                        table.SetAction(state.index, Vt, action);
                    }
                }
            }
        }
    }

    var result = new SLR1SyntaxInfo(stateList, edgeList, table);

    return result;
}

SLR(1)狀態求解閉包的演演算法與LR(0)完全相同。

LR(1)分析法

演演算法思想：

拿到第一個Regulation（Vn:V1 V2 V3 .. ;），以 Vn: ⏳ V1 V2 V3 .. ;為初始LR(1)狀態，並求解其閉包。實際上，第一個Regulation就是擴充套件Regulation。
對每個LR(1)狀態A，讓⏳向前移動一個V，得到下一個LR(1)狀態B，並求解其閉包。
將A-V->B設定為LR(1)邊。
設定LR(1)分析表：對每個LR(1)邊（例如A-V->B），若V是Vt，則在A行V列記錄移進到B；若V是Vn，則在A行V列記錄跳入B。
設定LR(1)分析表：對每個LR(1)狀態（例如A）中的每個Item，若Item中的⏳位於Regulation末尾，一般情況下，則在A行全部lookAhead列記錄用Regulation規約；特殊情況（Regulation是擴充套件Regulation）下，則在A行'¥'列記錄完成。

public static LR1SyntaxInfo GetLR1SyntaxInfo(this VnRegulationDraft[] regulations,
    VnRegulationDraft[] eRegulations, Dictionary<string, bool> eNullableDict, Dictionary<string, FIRST> eFIRSTDict) {
    var stateList = new LR1StateList();
    var edgeList = new LR1EdgeList();
    var eEnd = '¥';
    var queue = new Queue<LR1State>(); {
        var firstItem = LR1Item.GetItem(eRegulations[0], 0, eEnd);
        var firstState = new LR1State(firstItem); Closure(firstState, eRegulations, eNullableDict, eFIRSTDict);
        stateList.TryInsert(firstState);
        queue.Enqueue(firstState);
    }
    while (queue.Count > 0) {
        var from = queue.Dequeue();
        foreach (var item in from.Items) {
            string/*Node.type*/ V = item.nodeNext2Dot;
            if (V == null) { continue; }

            var to = Goto(from, V); to.Closure(eRegulations, eNullableDict, eFIRSTDict);
            if (stateList.TryInsert(to)) { // to是新狀態
                queue.Enqueue(to);
                var edge = new LR1Edge(from, V, to);
                edgeList.TryInsert(edge);
            }
            else { // to是已有狀態
                int t = stateList.IndexOf(to);
                var oldTo = stateList.States[t];
                var edge = new LR1Edge(from, V, oldTo);
                edgeList.TryInsert(edge);
            }
        }
    }

    var table = new LRParsingTableDraft();
    foreach (var edge in edgeList.Edges) {
        if (edge.V.IsVt()) {
            // shift in action
            table.SetAction(edge.from.index, edge.V, new LRShiftInActionDraft(edge.to.index));
        }
        else { // V is Vn
            // goto action
            table.SetAction(edge.from.index, edge.V, new LRGotoActionDraft(edge.to.index));
        }
    }
    var eLeft = eRegulations[0].left; // the S' in many books.
    foreach (var state in stateList.States) {
        foreach (var item in state.Items) {
            string/*Node.type*/ V = item.nodeNext2Dot;
            if (V == null) {
                if (item.VnRegulation.left == eLeft) {
                    // accept action
                    var action = new LRAcceptActionDraft();
                    table.SetAction(state.index, eEnd, action);
                }
                else {
                    // reduction action
                    int reductionIndex = Array.IndexOf(eRegulations, item.VnRegulation) - 1;
                    var action = new LRReducitonActionDraft(reductionIndex);
                    {
                        table.SetAction(state.index, item.lookAhead, action);
                    }
                }
            }
        }
    }

    var result = new LR1SyntaxInfo(stateList, edgeList, table);

    return result;
}

LR(1)狀態求解閉包的演演算法：

對LR(1)狀態中的每個Item（left : 某V 某V .. ⏳ V 某V1 某V2 .. ; z），若⏳後面的第一個V是Vn，則將所有的Vn : ⏳ V1 V2 V3 .. ; lookAhead加入此狀態，其中的lookAhead=FIRST(某V1 某V2 .. z)。
迭代至不再新增Item。

private static void Closure(this LR1State state, VnRegulationDraft[] eRegulations,
    Dictionary<string/*Node.type*/, bool> emptyDict, Dictionary<string, FIRST> firstDict) {
    var queue = new Queue<LR1Item>();
    foreach (var item in state.Items) { queue.Enqueue(item); }
    while (queue.Count > 0) {
        var item = queue.Dequeue();
        string/*Node.type*/ node = item.nodeNext2Dot;
        if (node == null || node.IsVt()) { continue; }

        nodeRegulations = eRegulations.GetVnRegulations(left: node);
        first = GetFIRST(item.betaZ, firstDict, emptyDict);
        foreach (var regulation in nodeRegulations) {
            foreach (var lookAhead in first.Values) {
                const int dotPosition = 0;
                var newItem = LR1Item.GetItem(regulation, dotPosition, lookAhead);
                if (state.TryInsert(newItem)) {
                    queue.Enqueue(newItem);
                }
            }
        }
    }
}

LALR(1)分析法

演演算法思想：

拿到第一個Regulation（Vn:V1 V2 V3 .. ;），以 Vn: ⏳ V1 V2 V3 .. ;為初始LR(1)狀態，並求解其閉包。實際上，第一個Regulations就是擴充套件Regulation。
對每個LR(1)狀態A，讓⏳向前移動一個V，得到下一個LR(1)狀態B，並求解其閉包。
將A-V->B設定為LR(1)邊。
設定LR(1)分析表：對每個LR(1)邊（例如A-V->B），若V是Vt，則在A行V列記錄移進到B；若V是Vn，則在A行V列記錄跳入B。
設定LR(1)分析表：對每個LR(1)狀態（例如A）中的每個Item，若Item中的⏳位於Regulation末尾，一般情況下，則在A行全部lookAhead列記錄用Regulation規約；特殊情況（Regulation是擴充套件Regulation）下，則在A行'¥'列記錄完成。

乍一看，LALR(1)演演算法與LR(1)演演算法完全相同。它們只在一點上有區別：Regulation相同、⏳位置相同而lookAhead不同的兩個狀態，在LALR(1)眼裡是相同的，在LR(1)眼裡是不同的。

public static LALR1SyntaxInfo GetLALR1SyntaxInfo(this VnRegulationDraft[] regulations,
    VnRegulationDraft[] eRegulations, Dictionary<string, bool> eEmptyDict, Dictionary<string, FIRST> eFIRSTDict) {
    var stateList = new LALR1StateList();
    var edgeList = new LALR1EdgeList();
    var eEnd = '¥';
    var queue = new Queue<LALR1State>(); {
        var firstItem = LALR1Item.GetItem(eRegulations[0], 0, eEnd);
        var firstState = new LALR1State(firstItem); Closure(firstState, eRegulations, eEmptyDict, eFIRSTDict);
        stateList.TryInsert(firstState);
        queue.Enqueue(firstState);
    }
    while (queue.Count > 0) {
        var from = queue.Dequeue();
        foreach (var item in from.Items) {
            string/*Node.type*/ V = item.nodeNext2Dot;
            if (V == null) { continue; }

            var to = Goto(from, V); to.Closure(eRegulations, eEmptyDict, eFIRSTDict);
            if (stateList.TryInsert(to)) { // to是新狀態
                queue.Enqueue(to);
                var edge = new LALR1Edge(from, V, to);
                edgeList.TryInsert(edge);
            }
            else { // to是已有狀態
                int t = stateList.IndexOf(to);
                var oldTo = stateList.States[t];

                // add lookAheads in toState to target.
                var updated = false;
                foreach (var item in to.Items) { if (oldTo.TryInsert(item)) { updated = true; } }
                if (updated) { queue.Enqueue(oldTo); }

                var edge = new LALR1Edge(from, V, oldTo);
                edgeList.TryInsert(edge);
            }
        }
    }
    
    var table = new LRParsingTableDraft();
    foreach (var edge in edgeList.Edges) {
        if (edge.V.IsVt()) {
            // shift in action
            table.SetAction(edge.from.index, edge.V, new LRShiftInActionDraft(edge.to.index));
        }
        else {
            // goto action
            table.SetAction(edge.from.index, edge.V, new LRGotoActionDraft(edge.to.index));
        }
    }
    var eLeft = eRegulations[0].left; // the S' in many books.
    foreach (var state in stateList.States) {
        foreach (var item in state.Items) {
            string/*Node.type*/ V = item.nodeNext2Dot;
            if (V == null) {
                if (item.VnRegulation.left == eLeft) {
                    // accept action
                    var action = new LRAcceptActionDraft();
                    table.SetAction(state.index, eEnd, action);
                }
                else {
                    // reduction action
                    int reductionIndex = Array.IndexOf(eRegulations, item.VnRegulation) - 1;
                    var action = new LRReducitonActionDraft(reductionIndex);
                    {
                        table.SetAction(state.index, item.lookAhead, action);
                    }
                }
            }
        }
    }

    var result = new LALR1SyntaxInfo(stateList, edgeList, table);

    return result;
}

LALR(1)狀態求解閉包的演演算法與LR(1)完全相同。

其他

快速比較兩個集合

LR(0)狀態、SLR(1)狀態、LALR(1)狀態、LR(1)狀態都是各自Item的集合。計算語法分析表時，需要比較兩個狀態是否相同，這實質上就是比較兩個集合包含的元素是否完全相同。

要想快速比較兩個集合是否相同，就得先排序，而後比較排序完畢的集合。如果對排序完畢的集合，先計算int Hashcode並快取之，那麼，只需比較兩個Hashcode是否相等即可。當然，如果集合新增了元素，就要重新計算Hashcode，這意味著需要有一個bool dirty;標記是否需要重新計算Hashcode。

在我們的應用場景裡，只需要新增元素，不需要修改或刪除元素，因而實現起來就簡單得多。

據此，我實現了對IList<T>的二分法快速插入演演算法：

    public static bool TryBinaryInsert<T>(this IList<T> list, T item)
        where T : IComparable<T> {
        bool inserted = false;

        if (list == null || item == null) { return inserted; }

        int left = 0, right = list.Count - 1;
        if (right < 0) {
            list.Add(item);
            inserted = true;
        }
        else {
            while (left < right) {
                int mid = (left + right) / 2;
                T current = list[mid];
                int result = item.CompareTo(current);
                if (result < 0) { right = mid; }
                else if (result == 0) { left = mid; right = mid; }
                else { left = mid + 1; }
            }
            {
                T current = list[left];
                int result = item.CompareTo(current);
                if (result < 0) {
                    list.Insert(left, item);
                    inserted = true;
                }
                else if (result > 0) {
                    list.Insert(left + 1, item);
                    inserted = true;
                }
            }
        }

        return inserted;
    }

擦除控制檯的文字

可以通過輸出退格符'\u0008'來退回到控制檯的上一個char的位置，相當於手動按一次鍵盤上的退格鍵（但不刪除char）。這在顯示進度的時候很有用。下面的程式碼可以擦除上次寫的內容，寫入新的內容：

    private static int lastOutputLength = 0;
    /// <summary>
    /// erase content written the last time and write something new.
    /// </summary>
    /// <param name="content"></param>
    public static void Rewrite(string content) {
        if (content == null) { content = string.Empty; }

        var currentLength = content.Length;
        var delta = lastOutputLength - currentLength;
        for (int t = 0; t < delta; t++) { Console.Write('\u0008'); } // move back
        for (int t = 0; t < delta; t++) { Console.Write(' '); } // erase with space
        for (int t = 0; t < lastOutputLength; t++) { Console.Write('\u0008'); } // move back 
        Console.Write(content);
        lastOutputLength = content.Length;
    }

用Mermaid畫圖

如果能畫出詞法分析自動機和語法分析狀態機的圖，會極大提升學習、開發、偵錯的效率。將自動機匯出為Mermaid格式的檔案(*.mmd)即可實現這個功能。本文的圖示，除了Calc文法的全部Token的自動機外，都是自動匯出的mmd檔案，在瀏覽器中實時渲染的。

ASCII碼

為處理正規表示式，我整理了ASCII碼及其10進位制和16進位製表，以便查閱。

 #032 !#033 "#034 ##035 $#036 %#037 &#038 '#039
(#040 )#041 *#042 +#043 ,#044 -#045 .#046 /#047
0#048 1#049 2#050 3#051 4#052 5#053 6#054 7#055 8#056 9#057
:#058 ;#059 <#060 =#061 >#062 ?#063 @#064
A#065 B#066 C#067 D#068 E#069 F#070 G#071 H#072 I#073 J#074
K#075 L#076 M#077 N#078 O#079 P#080 Q#081 R#082 S#083 T#084
U#085 V#086 W#087 X#088 Y#089 Z#090
[#091 \#092 ]#093 ^#094 _#095 `#096
a#097 b#098 c#099 d#100 e#101 f#102 g#103 h#104 i#105 j#106
k#107 l#108 m#109 n#110 o#111 p#112 q#113 r#114 s#115 t#116
u#117 v#118 w#119 x#120 y#121 z#122
{#123 |#124 }#125 ~#126

 \u20 !\u21 "\u22 #\u23 $\u24 %\u25 &\u26 '\u27
(\u28 )\u29 *\u2A +\u2B ,\u2C -\u2D .\u2E /\u2F
0\u30 1\u31 2\u32 3\u33 4\u34 5\u35 6\u36 7\u37 8\u38 9\u39
:\u3A ;\u3B <\u3C =\u3D >\u3E ?\u3F @\u40
A\u41 B\u42 C\u43 D\u44 E\u45 F\u46 G\u47 H\u48 I\u49 J\u4A
K\u4B L\u4C M\u4D N\u4E O\u4F P\u50 Q\u51 R\u52 S\u53 T\u54
U\u55 V\u56 W\u57 X\u58 Y\u59 Z\u5A
[\u5B \\u5C ]\u5D ^\u5E _\u5F `\u60
a\u61 b\u62 c\u63 d\u64 e\u65 f\u66 g\u67 h\u68 i\u69 j\u6A
k\u6B l\u6C m\u6D n\u6E o\u6F p\u70 q\u71 r\u72 s\u73 t\u74
u\u75 v\u76 w\u77 x\u78 y\u79 z\u7A
{\u7B |\u7C }\u7D ~\u7E

  ! " # $ % & '
( ) * + , - . /
0 1 2 3 4 5 6 7 8 9
: ; < = > ? @
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
[ \ ] ^ _ `
a b c d e f g h i j k l m
n o p q r s t u v w x y z
{ | } ~

總結

近期有其他事務要處理，不得不暫停。目前還有這幾個問題沒有寫完：

把詞法分析過程、語法分析過程、語意分析過程、分析表生成過程都匯出為更生動的gif動圖。
在文法中增加對註釋Token的支援，免去手動新增識別註釋的麻煩。
修改Grammar的設定，讓多個%%xxx%%指向同一個Vt。這才更接近lex的功能。
優化識別關鍵字的程式碼：不將關鍵字納入Automaton，減少囉嗦的狀態。
使用特殊邊，避免遇到[a-z]{min, max}時批次複製子regex。
支援錯誤處理功能。

如果讀者想認真學本文介紹的演演算法，但耐心不足，可以看看（https://www.cnblogs.com/bitzhuwei/p/explore-compiling.html）。

編譯原理（前端）的演演算法和實現

編譯原理（前端）的演演算法和實現

練手預熱——四則運算解析器CompilerCalc

詞法分析器

語法分析器

文法裡都有什麼

語法分析三大件

nullable(VList)

FIRST(VList)

FOLLOW(Vn)

LL(1)分析法

LR(0)分析法

SLR(1)分析法

LR(1)分析法

LALR(1)分析法

LR分析法小結

語意分析器

其它

進入正題——文法解析器CompilerGrammar

一鍵生成詞法分析器

字首<'xxx'>

字尾/post-regex

ε-NFA

NFA

DFA

MiniDFA

一鍵生成語法分析器

計算nullable(VList)

計算FIRST(VList)

計算FOLLOW(Vn)

擴充套件文法

LL(1)分析法

LR(0)分析法

SLR(1)分析法

LR(1)分析法

LALR(1)分析法

其他

快速比較兩個集合

擦除控制檯的文字

用Mermaid畫圖

ASCII碼

總結

練手預熱——四則運算解析器`CompilerCalc`

進入正題——文法解析器`CompilerGrammar`