技術文章 » LeetCode 雙週賽 104（2023/05/13）流水的動態規劃，鐵打的結構化思考

LeetCode 雙週賽 104（2023/05/13）流水的動態規劃，鐵打的結構化思考

2023-05-15 06:01:25

本文已收錄到 AndroidFamily，技術和職場問題，請關注公眾號 [彭旭銳] 提問。

T1. 老人的數目（Easy）

  • 標籤：模擬、計數

T2. 矩陣中的和（Medium）

  • 標籤：模擬、排序

T3. 最大或值（Medium）

  • 標籤：動態規劃、前字尾分解、貪心

T4. 英雄的力量（Hard）

  • 標籤：排序、貪心、動態規劃、數學

T1. 老人的數目（Easy）

https://leetcode.cn/problems/number-of-senior-citizens/

簡單模擬題，直接擷取年齡字元后計數即可：

class Solution {
    fun countSeniors(details: Array<String>): Int {
        return details.count { it.substring(11, 13).toInt() > 60 }
    }
}

除了將字串轉為整數再比較外，還可以直接比較子串與 「60」 的字典序：

class Solution {
    fun countSeniors(details: Array<String>): Int {
        return details.count { it.substring(11, 13) > "60" }
    }
}

複雜度分析：

  • 時間複雜度：$O(n)$ 其中 n 為 details 陣列的長度；
  • 空間複雜度：$O(1)$ 僅使用常數級別空間。

T2. 矩陣中的和（Medium）

https://leetcode.cn/problems/sum-in-a-matrix/

簡單模擬題。

先對每一行排序，再取每一列的最大值。

class Solution {
    fun matrixSum(nums: Array<IntArray>): Int {
        var ret = 0
        for (row in nums) {
            row.sort()
        }
        for (j in 0 until nums[0].size) {
            var mx = 0
            for (i in 0 until nums.size) {
                mx = Math.max(mx, nums[i][j])
            }
            ret += mx
        }
        return ret
    }
}

複雜度分析：

  • 時間複雜度：$O(nmlgm + nm)$ 其中 n 和 m 分別為矩陣的行數和列數，排序時間 $O(nmlgm)$，掃描時間 $O(nm)$；
  • 空間複雜度：$O(lgm)$ 排序遞迴棧空間。

T3. 最大或值（Medium）

https://leetcode.cn/problems/maximum-or/

題目描述

給你一個下標從 0 開始長度為 n 的整數陣列 nums 和一個整數 k 。每一次操作中，你可以選擇一個數並將它乘 2 。

你最多可以進行 k 次操作，請你返回 **nums[0] | nums[1] | ... | nums[n - 1] 的最大值。

a | b 表示兩個整數 a 和 b 的 按位元或 運算。

範例 1：

輸入：nums = [12,9], k = 1
輸出：30
解釋：如果我們對下標為 1 的元素進行操作，新的陣列為 [12,18] 。此時得到最優答案為 12 和 18 的按位元或運算的結果，也就是 30 。

範例 2：

輸入：nums = [8,1,2], k = 2
輸出：35
解釋：如果我們對下標 0 處的元素進行操作，得到新陣列 [32,1,2] 。此時得到最優答案為 32|1|2 = 35 。

提示：

  • 1 <= nums.length <= 105
  • 1 <= nums[i] <= 109
  • 1 <= k <= 15

問題結構化

1、概括問題目標

計算可以獲得的最大或值。

2、分析問題要件

在每次操作中，可以從陣列中選擇一個數乘以 2，亦相當於向左位移 1 位。

3、觀察問題資料

  • 資料量：問題資料量上界為 $10^5$，要求演演算法時間複雜度低於 $O(n^2)$；
  • 資料大小：元素值的上界為 $10^9$，操作次數 k 的上界為 15（這個性質有什麼用呢？）；
  • 輸出結果：以長整型 Long 的形式返回結果。

4、觀察測試用例

以範例 1 nums=[12, 9], k = 1 為例，最優答案是對 9 乘以 2，說明操作最大值並不一定能獲得最大或值。

5、提高抽象程度

  • 權重：二進位制位越高的位對數位大小的影響越大，因此我們應該儘量讓高位的二進位制位置為 1；
  • 是否為決策問題？由於每次操作有多種位置選擇，因此這是一個決策問題。

6、具體化解決手段

  • 1、貪心：結合「資料大小」分析，由於操作次數 k 的上界為 15 次，無論如何位移都不會溢位 Long。因此，我們可以將 k 次位移操作作用在同一個數位上，儘可能讓高位的位置置為 1；
  • 2、動態規劃（揹包）：假設已經計算出陣列前 i - 1 個元素能夠組成的最大或值，那麼考慮拼接 nums[i]，可以選擇不操作 nums[i]，也可以選擇在 nums[i] 上操作 x 次，那麼問題就變成「前 i - 1 個元素中操作 k - x 次的最大或值」與「num[i] 操作 x 次的或值」合併的或值。「前 i - 1 個元素中操作 k - x 次的最大或值」這是一個與原問題相似但規模更小的子問題，可以用動態規劃解決，更具體地可以用揹包問題模型解決。

題解一（貪心 + 前字尾分解）

列舉所有數位並向左位移 k 次，計算所有方案的最優解：

class Solution {
    fun maximumOr(nums: IntArray, k: Int): Long {
        val n = nums.size
        // 前字尾分解
        val pre = IntArray(n + 1)
        val suf = IntArray(n + 1)
        for (i in 1 .. n) {
            pre[i] = pre[i - 1] or nums[i - 1]
        }
        for (i in n - 1 downTo 0) {
            suf[i] = suf[i + 1] or nums[i]
        }
        var ret = 0L
        for (i in nums.indices) {
            ret = Math.max(ret, (1L * nums[i] shl k) or pre[i].toLong() or suf[i + 1].toLong())
        }
        return ret
    }
}

由於每個方案都需要列舉前後 n - 1 個數位的或值，因此這是一個 $O(n^2)$ 的解法，會超出時間限制。我們可以採用空間換時間的策略，預先計算出每個位置（不包含）的前字尾的或值，這個技巧就是「前字尾分解」。

在實現細節上，我們可以把其中一個字首放在掃描的時候處理。

class Solution {
    fun maximumOr(nums: IntArray, k: Int): Long {
        val n = nums.size
        // 前字尾分解
        val suf = IntArray(n + 1)
        for (i in n - 1 downTo 0) {
            suf[i] = suf[i + 1] or nums[i]
        }
        var ret = 0L
        var pre = 0L
        for (i in nums.indices) {
            ret = Math.max(ret, pre or (1L * nums[i] shl k) or suf[i + 1].toLong())
            pre = pre or nums[i].toLong()
        }
        return ret
    }
}

複雜度分析：

  • 時間複雜度：$O(n)$ 其中 n 為 nums 陣列的長度；
  • 空間複雜度：$O(n)$ 字尾或值陣列長度空間。

題解二（動態規劃）

使用揹包問題模型時，定義 dp[i][j] 表示在前 i 個元素上操作 k 次可以獲得的最大或值，則有：

  • 狀態轉移方程：$dp[i][j] = max{dp[i-1][j], dp[i - 1][j - x] | (nums[i] << x)}$
  • 終止條件：$dp[n][k]$
 class Solution {
    fun maximumOr(nums: IntArray, k: Int): Long {
        val n = nums.size
        // 以 i 為止，且移動 k 次的最大或值
        val dp = Array(n + 1) { LongArray(k + 1) }
        for (i in 1 .. n) {
            for (j in 0 .. k) {
                for (m in 0 .. j) {
                    dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - m] or (1L * nums[i - 1] shl m) /* 移動 m 次 */)
                }
            }
        }
        return dp[n][k]
    }
}

另外，這個揹包問題可以取消物品維度來優化空間：

class Solution {
    fun maximumOr(nums: IntArray, k: Int): Long {
        val n = nums.size
        // 以 i 為止，且移動 k 次的最大或值
        val dp = LongArray(k + 1)
        for (i in 1 .. n) {
            // 逆序
            for (j in k downTo 0) {
                for (m in 0 .. j) {
                    dp[j] = Math.max(dp[j], dp[j - m] or (1L * nums[i - 1] shl m) /* 移動 m 次 */)
                }
            }
        }
        return dp[k]
    }
}
  • 時間複雜度：$O(n·k^2)$ 其中 n 為 nums 陣列的長度；
  • 空間複雜度：$O(k)$ DP 陣列空間

相似題目：

T4. 英雄的力量（Hard）

https://leetcode.cn/problems/power-of-heroes/

題目描述

給你一個下標從 0 開始的整數陣列 nums ，它表示英雄的能力值。如果我們選出一部分英雄，這組英雄的 力量 定義為：

  • i0 ，i1 ，... ik 表示這組英雄在陣列中的下標。那麼這組英雄的力量為 max(nums[i0],nums[i1] ... nums[ik])2 * min(nums[i0],nums[i1] ... nums[ik]) 。

請你返回所有可能的 非空 英雄組的 力量 之和。由於答案可能非常大，請你將結果對 109 + 7 取餘。

範例 1：

輸入：nums = [2,1,4]
輸出：141
解釋：
第 1 組：[2] 的力量為 22 * 2 = 8 。
第 2 組：[1] 的力量為 12 * 1 = 1 。
第 3 組：[4] 的力量為 42 * 4 = 64 。
第 4 組：[2,1] 的力量為 22 * 1 = 4 。
第 5 組：[2,4] 的力量為 42 * 2 = 32 。
第 6 組：[1,4] 的力量為 42 * 1 = 16 。
第 7 組：[2,1,4] 的力量為 42 * 1 = 16 。
所有英雄組的力量之和為 8 + 1 + 64 + 4 + 32 + 16 + 16 = 141 。

範例 2：

輸入：nums = [1,1,1]
輸出：7
解釋：總共有 7 個英雄組，每一組的力量都是 1 。所以所有英雄組的力量之和為 7 。

提示：

  • 1 <= nums.length <= 105
  • 1 <= nums[i] <= 109

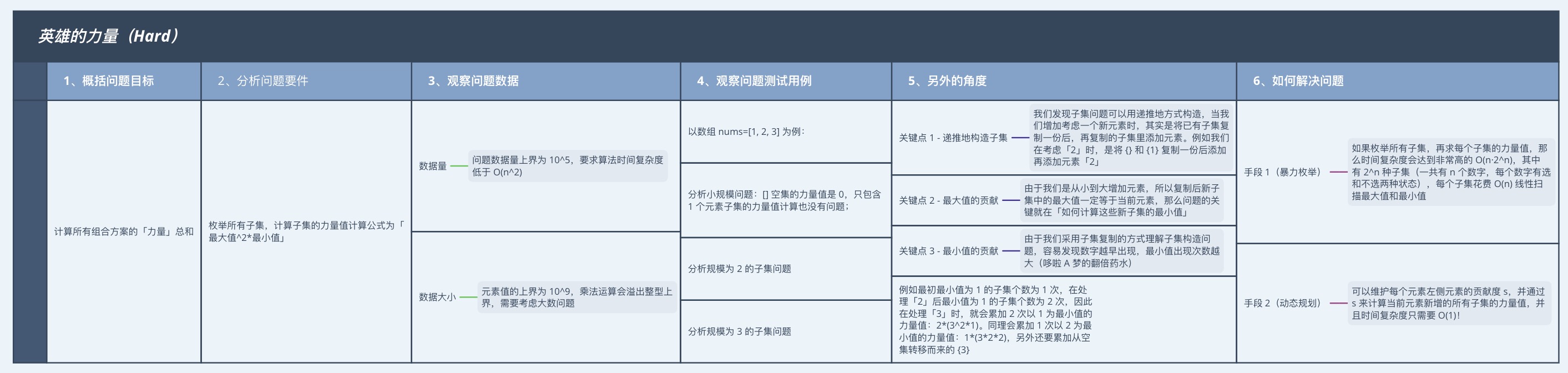
問題結構化

1、概括問題目標

計算所有組合方案的「力量」總和。

2、分析問題要件

列舉所有子集，計運算元集的力量值計算公式為$「最大值^2*最小值」$。

3、觀察問題資料

  • 資料量：問題資料量上界為 $10^5$，要求演演算法時間複雜度低於 $O(n^2)$；
  • 資料大小：元素值的上界為 $10^9$，乘法運算會溢位整型上界，需要考慮大數問題。

4、觀察問題測試用例：

以陣列 nums=[1, 2, 3] 為例：

  • 分析小規模問題：[] 空集的力量值是 0，只包含 1 個元素子集的力量值計算也沒有問題；
子集 最大值 最小值 力量值
{} 0 0 0
1 1 $1^2*1$
2 2 $2^2*2$
3 3 $3^2*3$
  • 分析規模為 2 的子集問題：
子集 最大值 最小值 力量值
2 1 $2^2*1$
3 1 $3^2*1$
3 2 $3^2*2$
  • 分析規模為 3 的子集問題：
子集 最大值 最小值 力量值
3 1 $3^2*1$

5、如何解決問題

  • 手段 1（暴力列舉）：如果列舉所有子集，再求每個子集的力量值，那麼時間複雜度會達到非常高的 $O(n·2^n)$，其中有 $2^n$ 種子集（一共有 n 個數位，每個數位有選和不選兩種狀態），每個子集花費 $O(n)$ 線性掃描最大值和最小值。

至此，問題陷入瓶頸，解決方法是重複以上步驟，列舉掌握的資料結構、演演算法和技巧尋找思路，突破口在於從另一個角度來理解問題規模（動態規劃的思路）。

6、繼續觀察問題測試用例

同樣以陣列 nums = [1, 2, 3] 為例：

  • 考慮空集的力量值問題：
子集 最大值 最小值
{} 0 0
  • 考慮到「1」為止的力量值問題：
子集 最大值 最小值
{} 0 0
1 1
  • 考慮到「2」為止的力量值問題：
子集 最大值 最小值
{} 0 0
1 1
2 2
2 1
  • 考慮到「3」為止的力量值問題：
子集 最大值 最小值
{} 0 0
1 1
2 2
2 1
3 3
3 1
3 2
3 1

這又說明了什麼呢？

  • 關鍵點 1 - 遞推地構造子集：

我們發現子集問題可以用遞推地方式構造，當我們增加考慮一個新元素時，其實是將已有子集複製一份後，再複製的子集裡新增元素。例如我們在考慮「2」時，是將 {} 和 {1} 複製一份後新增再新增元素「2」。

  • 關鍵點 2 - 最大值的貢獻：

由於我們是從小到大增加元素，所以複製後新子集中的最大值一定等於當前元素，那麼問題的關鍵就在「如何計算這些新子集的最小值」。

  • 關鍵點 3 - 最小值的貢獻：

由於我們採用子集複製的方式理解子集構造問題，容易發現數位越早出現，最小值出現次數越大（哆啦 A 夢的翻倍藥水）。

例如最初最小值為 1 的子集個數為 1 次，在處理「2」後最小值為 1 的子集個數為 2 次，因此在處理「3」時，就會累加 2 次以 1 為最小值的力量值：$2(3^21)$。同理會累加 1 次以 2 為最小值的力量值：$1(32*2)$，另外還要累加從空集轉移而來的 {3}。

至此，問題的解決辦法逐漸清晰。

7、解決問題的新手段

  • 手段 2（動態規劃）：

考慮有 a, b, c, d, e 五個數，按順序從小到大排列，且從小到大列舉。

當列舉到 d 時，複製增加的新子集包括：

  • 以 a 為最小值的子集有 4 個：累加力量值 $4(d^2a)$
  • 以 b 為最小值的子集有 2 個：累加力量值 $2(d^2b)$
  • 以 c 為最小值的子集有 1 個：累加力量值 $1(d^2c)$

另外還有以 d 本身為最小值的子集 1 個：累加力量值 $1(d^2d)$，將 d 左側元素對結果的貢獻即為 s，則有 $pow(d) = d^2*(s + d)$。

繼續列舉到 e 是，複製增加的新子集包括：

  • 以 a 為最小值的子集有 8 個：累加力量值 $8(e^2a)$
  • 以 b 為最小值的子集有 4 個：累加力量值 $4(e^2b)$
  • 以 c 為最小值的子集有 2 個：累加力量值 $2(e^2c)$
  • 以 d 為最小值的子集有 1個：累加力量值 $1(e^2d)$

另外還有以 e 本身為最小值的子集 1 個：累加力量值 $1(e^2e)$，將 e 左側元素對結果的貢獻即為 s`，則有 $pow(e) = e^2*(s` + e)$。

觀察 s 和 s` 的關係：

$s = 4a + 2b + 1*c$

$s = 8a + 4b + 2c + d = s2 + d$

這說明，我們可以維護每個元素左側元素的貢獻度 s，並通過 s 來計算當前元素新增的所有子集的力量值，並且時間複雜度只需要 O(1)！

[4,3,2,1]
 1 1 2 4
追加 5：
[5,4,3,2,1]
 1 1 2 4 8

題解（動態規劃）

根據問題分析得出的遞迴公式，使用遞推模擬即可，先不考慮大數問題：

class Solution {
    fun sumOfPower(nums: IntArray): Int {
        var ret = 0L
        // 排序
        nums.sort()
        // 影響因子
        var s = 0L
        for (x in nums) {
            ret += (x * x) * (s + x)
            s = s * 2 + x
        }
        return ret.toInt()
    }
}

再考慮大數問題：

class Solution {
    fun sumOfPower(nums: IntArray): Int {
        val MOD = 1000000007
        var ret = 0L
        // 排序
        nums.sort()
        // 影響因子
        var s = 0L
        for (x in nums) {
            ret = (ret + (1L * x * x % MOD) * (s + x)) % MOD // x*x 也可能溢位
            s = (s * 2 + x) % MOD
        }
        return ret.toInt()
    }
}

實戰中我用的是先計算最大影響因子，再累減的寫法：

class Solution {
    fun sumOfPower(nums: IntArray): Int {
        val MOD = 1000000007
        var ret = 0L
        val n = nums.size
        // 排序
        nums.sortDescending()
        // 影響因子
        var s = 0L
        var p = 1L
        for (i in 1 until n) {
            s = (s + nums[i] * p) % MOD 
            p = (2 * p) % MOD
        }
        // 列舉子集
        for (i in 0 until n) {
            val x = nums[i]
            ret = (ret + x * x % MOD * (s + x)) % MOD
            if (i < n - 1) {
                s = (s - nums[i + 1]) % MOD
                if (s and 1L != 0L) {
                    s += MOD // 奇數除 2 會丟失精度
                }
                s = (s / 2) % MOD
            }
        }
        return ret.toInt()
    }
}

複雜度分析：

  • 時間複雜度：$O(nlgn)$ 其中 n 為 nums 陣列的長度，瓶頸在排序上，計算力量值部分時間複雜度為 O(n)；
  • 空間複雜度：$O(lgn)$ 排序遞迴棧空間。

往期回顧