題目：

給定N個整數的序列{ A1,A2,....An }，求函數F（i，j）=Max{ Ai+.....Aj  }

題目要求：

這道題的目的是要求給定的一個整數序列中，它所含的連續子序列的最大值，比如現在我有一個整數序列{ -3，2，3，-3，1}

它的最大子序列很顯然是  { 2，3 }

第一種方法蠻力法（強制列舉）：

我們從第一個整數開始遍歷，依次計算一個一個的加起來，知道最後一個元素，我們不斷的往後加的時候會一直更新最大的子序列，有情況是從頭加到尾不是最大的，它在中間就已經是最大的

所以我們需要在沒加一個就更新最大的子序列，當加到最後一個元素時

就換一個元素開始，比如從第二個元素開始，完了就第三個，就這麼一直換了換的加，一直到使用最後一個元素開始計算時就結束

我們用舉例圖片來描述一下我們的蠻力法：

 

 

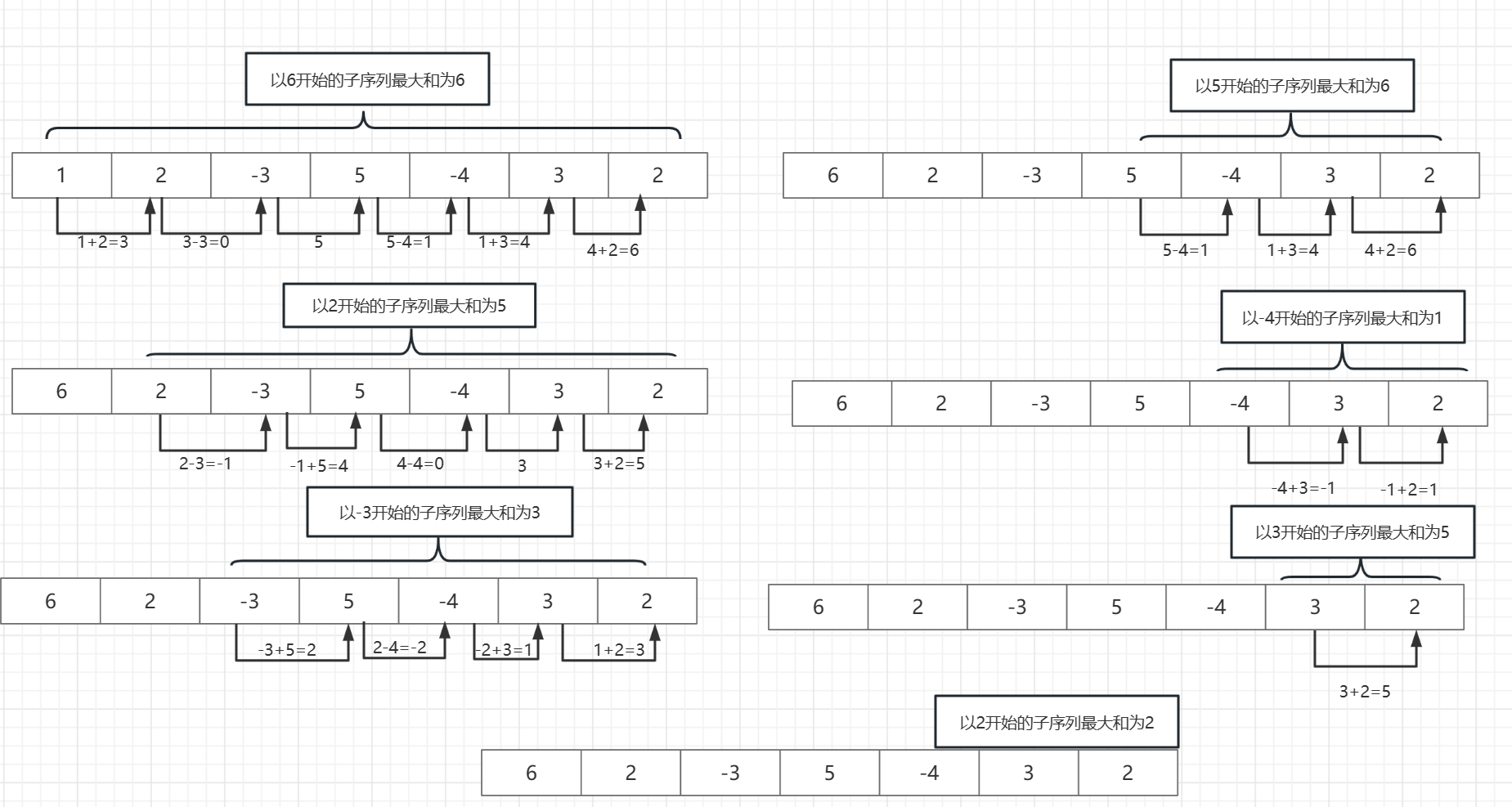
在第一次從第一個元素開始時候，我們的最大子序列和是依次動態更新為 1 ，3 ，5 ，6

在第二次從第二個元素開始時候，我們的最大子序列和是依次動態更新為 （未更新）

在第三次從第三個元素開始時候，我們的最大子序列和是依次動態更新為 （未更新）

在第四次從第四個元素開始時候，我們的最大子序列和是依次動態更新為 6

在第五次從第五個元素開始時候，我們的最大子序列和是依次動態更新為 （未更新）

在第六次從第六個元素開始時候，我們的最大子序列和是依次動態更新為 （未更新）

在第七次從第七個元素開始時候，我們的最大子序列和是依次動態更新為 （未更新）

綜上：蠻力法的結果為 最大子序列為{ 5，-4，3，2 } ，最大子序列和為 6

現在我們使用虛擬碼實現一下這個演演算法：

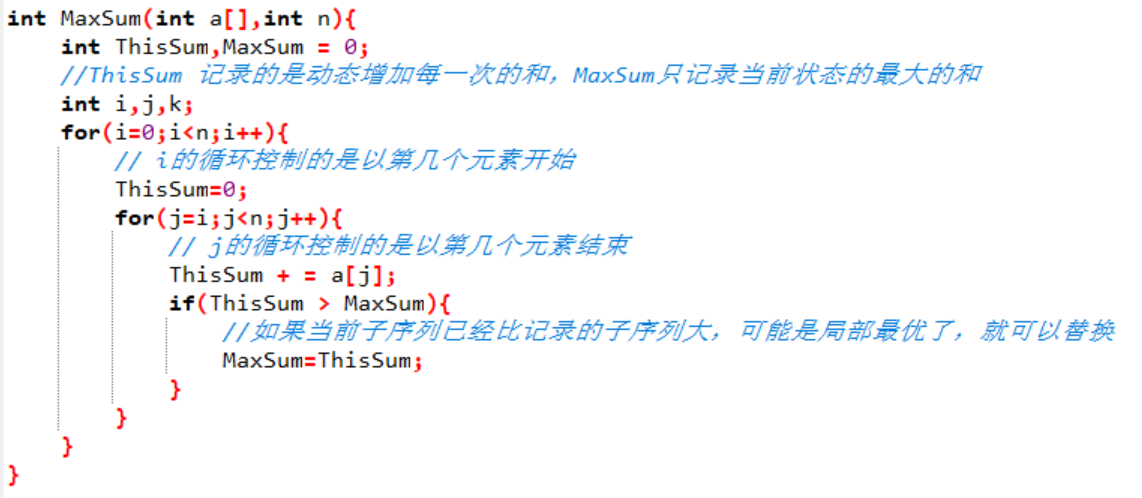
 我們可以根據這個虛擬碼很快的計算出它的時間複雜度，有兩個for迴圈，很明顯的就是T(n) = O(n^2)

作為一個程式猿，我們在程式碼的時間複雜度為n平方時，我們要很自覺的要想到對複雜度進行降級，當n的數位變大時，n的平方就會以倍速增長，

所以，我們要考慮把這個複雜度降到 n log 2^n  ，或者更好的  n 級 ，還有 log n

即使不能降到那麼低也要考慮試試能不能降到 n log 2^n

二.分而治之（分治法）：

首先我們來了解一下什麼是分而治之？

分治法，字面意思是「分而治之」，就是把一個複雜的1問題分成兩個或多個相同或相似的子問題，再把子問題分成更小的子問題直到最後子問題可以簡單地直接求解，原問題的解即子問題的解的合併，這個思想是很多高效演演算法的基礎，

這個演演算法的簡單思路就是：

• 先把一個大問題有規律有技巧的分為小問題
• 對小問題進行計算，按要求求解（此方法的解決思想是解決小問題比直接解決大問題要簡單）
• 再把計算好的結果或答案，按要求進行組合歸併

基於這個演演算法還衍生了很多其它演演算法：但是並未完全使用到它的思想，都只用了一部分

最耳熟能詳的就是：

1.二分查詢：利用了 分解問題和計算問題的思想

2.歸併排序：利用了 計算問題和合並求解的思想

此題的分治法解決思路：

這裡，我們對於這個整數序列就可以使用這樣的方法，我們先把這個序列一直劃分，劃分到左右兩邊要麼只有一個元素要麼只有一個元素的時候就可以計算了，

當劃分到最小單元以後，左右兩邊都能計算出一個最大的序列，這個序列在最底層還是隻有一個元素的，所以長度為一，大小就是它自己，

然後就回溯，回溯的過程中我們可能存在兩個序列組合後才是最大的情況，所以我們要對其合併後的序列進行掃描，看看合併的序列比未合併的序列是否要大一些

如果合併序列比子序列大，那麼合併序列才是最大子序列，反之，就看看左右兩邊那邊的子序列大，大的就作為返回值，繼續回溯，

直到回溯到最開始呼叫函數的時候，函數就執行完成，這個返回值就是最大子序列和

我們給定一個序列，然後按照分而治之的思想一步一步的做：

第一步：把大問題拆解成一個個小問題

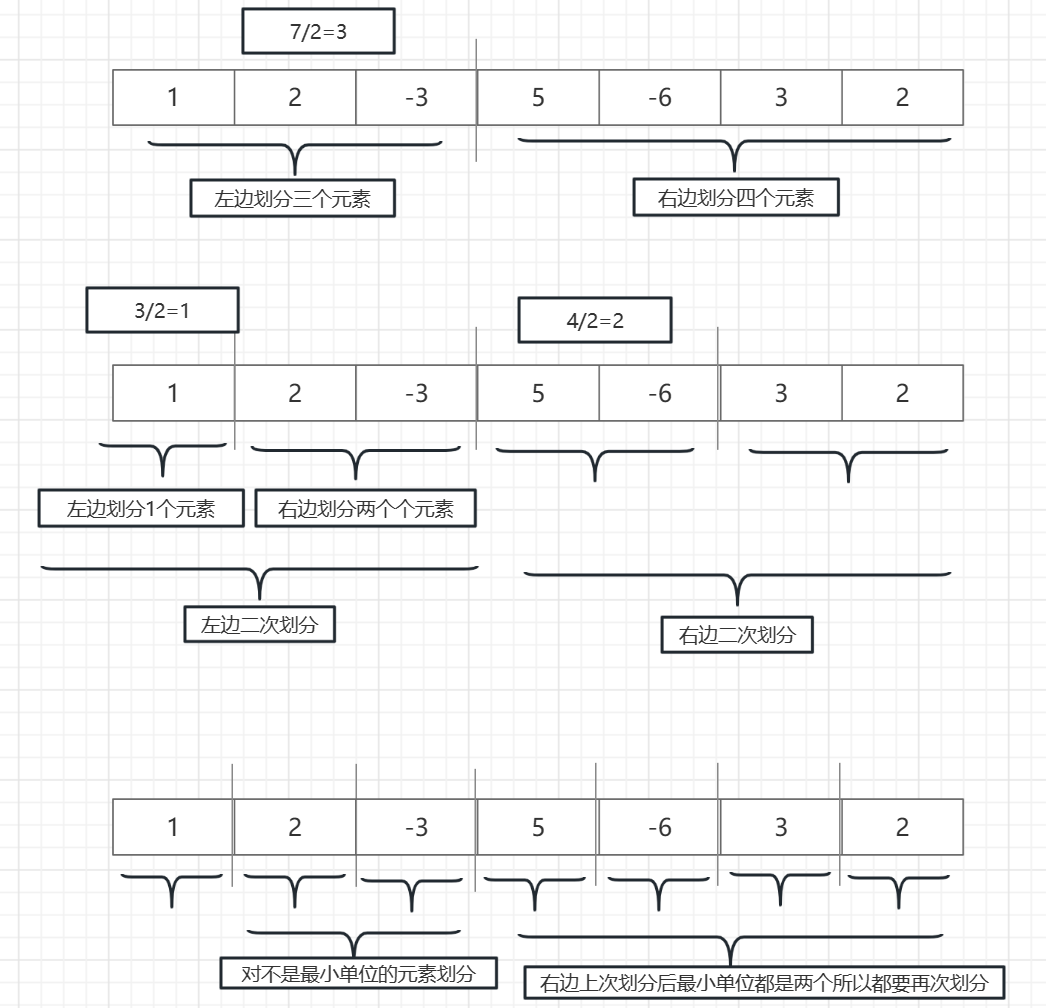
 如圖：我們把一個七元素的序列，劃分成了七分只有一元素的子序列

當圖片上的步驟完成以後，我們的第一步也就完成了，把大問題花小，這個時候我們這些小序列中誰的大就返回到上一級

第二步：對小問題進行求解，向上一級帶回自己所計算的引數

在計算的時候：一定要保證資料已經到達最小單位，比如這裡我們是一個陣列的話，那每一個最小序列必須是單個的陣列元素以後才能計算

在合併計算時，左邊會返回一個子序列的最大值，右邊也會有一個，但是不一定合併後的子序列它們會是最大的序列和，我們要進行合併掃描

合併掃描左邊區域和右邊區域的掃描都要從中間斷點開始，然後將掃描出的結果和左邊返回值，右邊返回值對比，大的才是這次劃分的最終答案

思考：大家可以想想為什麼左右兩邊，都要從中間開始向兩邊掃描（思路是連續最小序列和）

第三步：把計算好的結果，按要求進行組合回溯（或引數迴帶）

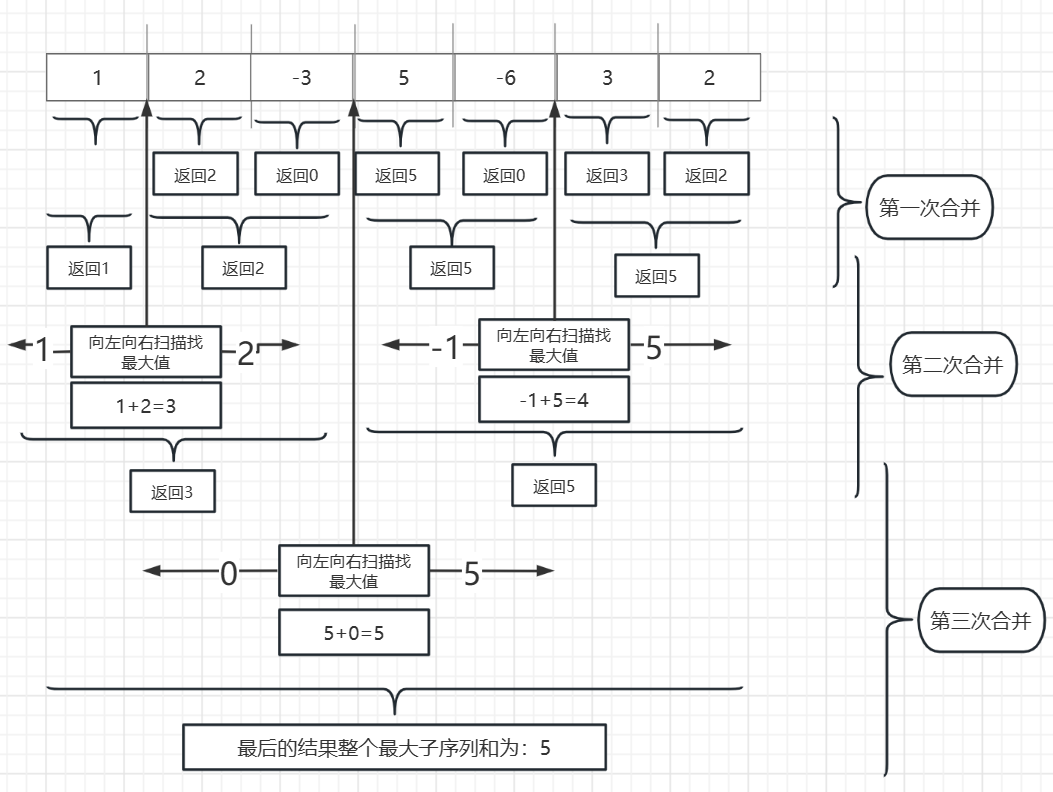
 如圖，從最低層開始，我們只要把左右兩邊的結果計算出來以後就已經開始合併了，每次拆分都對應著一次合併，

它們在合併後又開始新的計算，只要合併到最高層以後就有了最後的結果

下面我們用虛擬碼來看看這個演演算法的實現：

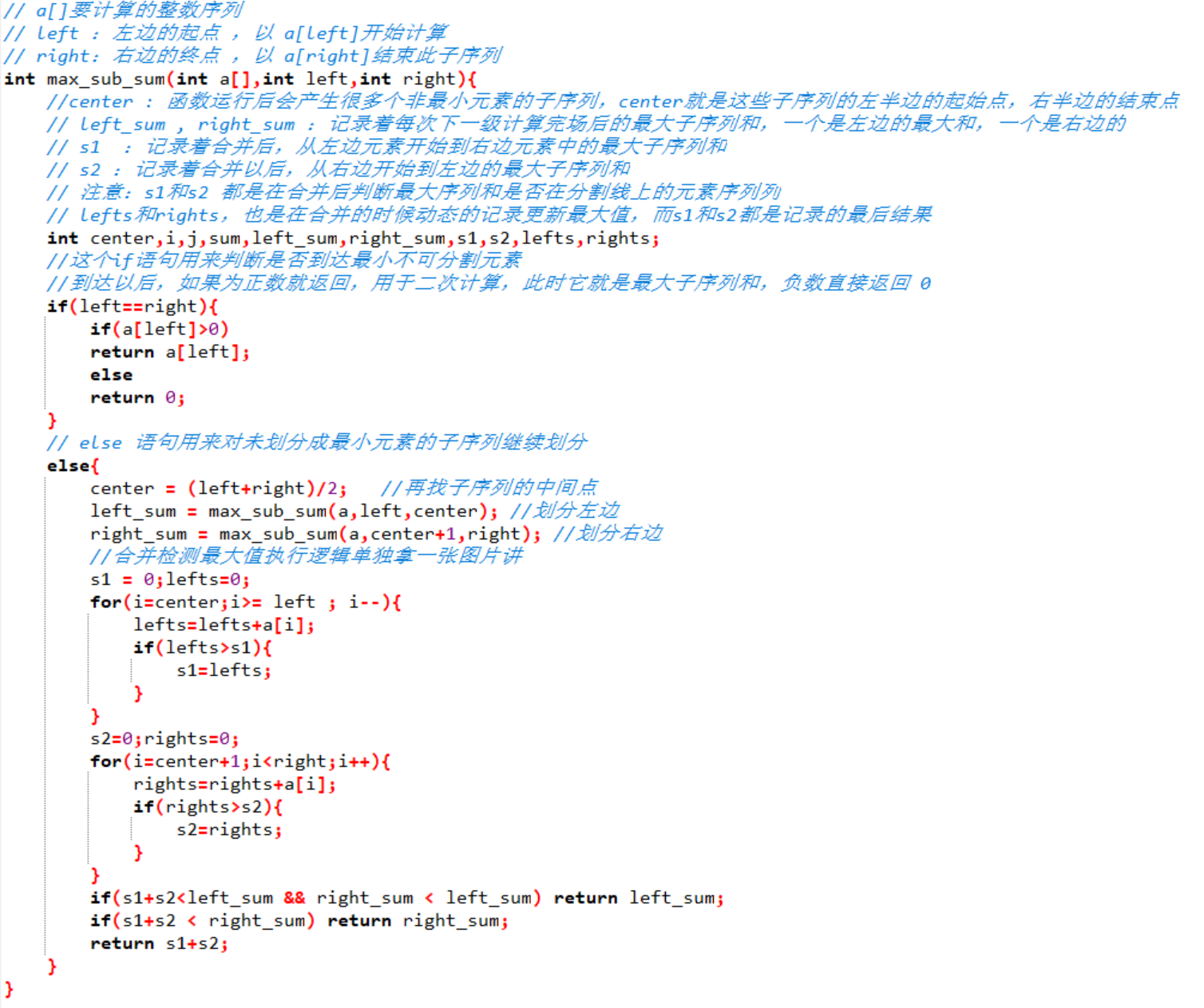
 分治法在開始的時候會不斷的拆分，當left = = right的時候，說明這資料下標就是它自己，就達到了我們要求的最小元素的要求，就可以計算後迴帶了

這裡都還好理解，對於左右兩邊要返回一個最大子序列和沒問題，主要的重點在於，合併時怎麼計算分界點是否才是那個最大子序列

所以這裡我們特別講解一下這個左右掃描的思路：

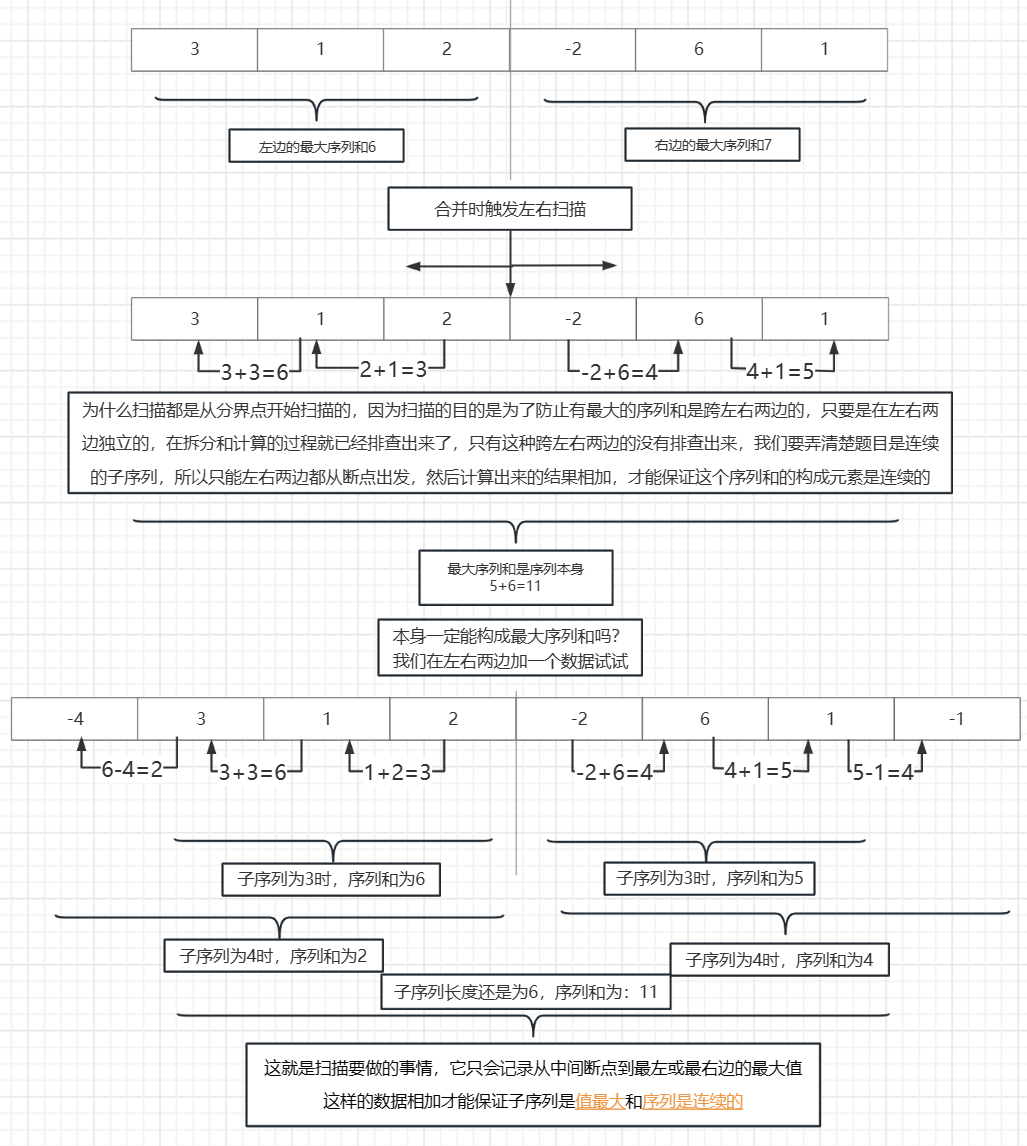
我們試著構造一個序列  { 3，1，2，-2，6，1 }，當回溯到最後一次拆分時，

左邊的最大子序列和是： 3+1+2 =6

右邊的最大子序列和是：6+1=7

結果 7 不一定是最後的總的最大子序列和，我們這個時候就來掃描一下，左邊的區域要從 2 開始向 左邊掃描  然後實時更新最大序列和，很顯然掃描完成以後最大序列和是： 2+1+3=6

然後就是右邊區域，它需要從-2開始向右邊掃描，掃描完成以後的值是： -2+6+1=5

最後左右關聯起來的最大子序列和為 ：5+6=11

綜上：

11 > 7 >6

所以這個全序列才能構成最大的子序列和，並不是左右兩邊的資料構成的

 

以上就是分治法的解題思路了，我們一起來看看分治法的時間複雜度是多少吧

由於分治法的時間開銷主要是，拆分和合並，所以計算方法也有點不同

我們可以簡單的看一下，每拆分一次，左邊右邊都需要花費T（n/2）的時間，然後每次合併的掃描時間 就是O（n）也就是掃描會把每個被合併的元素一個一個都遍歷一遍

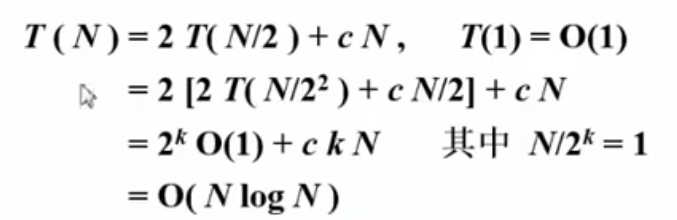
 所以，最後分治法解決這一道題的時間複雜度是：O(N log N)

三.線上處理演演算法（Online Algorithm）

線上處理（Online Algorithm）是一種在資料流到達時實時處理資料的演演算法。線上處理演演算法需要在沒有全部資料的情況下，即時處理當前接收到的資料，並根據已有的區域性資訊做出相應的決策，同時保證最終的全域性結果是正確的。

線上處理演演算法就很神奇，它好像活得一樣，不管你輸入的資料有沒有輸完，它總能根據已輸入的資料先做出判斷然後給出答案，感覺有和貪婪演演算法一樣，以區域性最優解以定全域性最優解

這一題我們使用線上處理演演算法的思路：

從第一元素開始遍歷，依次向後加上後面的元素，當我們的加到後面的元素，所計算的結果集還是整數，就一直和已經記錄的最大值比較，時刻記錄著最大值，

當加到某個元素為負數時，這時候直接清零，從這個元素開始從新記錄，因為負數不管後面元素是什麼，都只會讓這個子序列和變小

從新記錄的是當前最大值，我們在前面記錄的最大值還存在，要是從新記錄的最大值是比原來的大，依舊可以更新最終的最大值

 線上處理的有點很明顯它的處理速度很快時間複雜度達到了O（n），對於任何一種演演算法來說，我們至少要把資料遍歷一遍，所以這個演演算法已經算是最優的了

 線上處理方法實現比較簡單，執行速度快，也會導致它的正確性不是很明顯

而且它只能執行依次，不可重複用，比如給它一串資料，它的執行邏輯是掃描完一個就會丟掉，尤其是清零時候，前面的資料原值直接就全部沒有了

我們可以思考一下：這種演演算法的會不會發生錯誤？或者它能保證不管任何整數序列都可以拿到正確的最大序列和嗎？

四.動態規劃

我們說了，線上處理已經把時間複雜度降到完美了，所以我們這裡的動態規劃就作為一個拓展，動態規劃的時間複雜的根據所給的題目有關，是不穩定的 常見的有：O(n^2) , O(n^3)

但是如果能構造到最優解，也可以達到 O(n)

什麼是動態規劃？

動態規劃（英語：Dynamic programming，簡稱 DP），是一種在數學、管理科學、電腦科學、經濟學和生物資訊學中使用的，通過把原問題分解為相對簡單的子問題的方式求解複雜問題的方法。動態規劃常常適用於有重疊子問題和最優子結構性質的問題。

以上定義來自維基百科，看定義感覺還是有點抽象。簡單來說，動態規劃其實就是，給定一個問題，我們把它拆成一個個子問題，直到子問題可以直接解決。然後呢，把子問題答案儲存起來，以減少重複計算。再根據子問題答案反推，得出原問題解的一種方法。

再具體一點，它會把算過的值記住，然後下一個計算可能會基於這個值來計算，減少了重複的計算，原始資料只會計算一次，每多一個資料，都是基於已經計算過的結果計算，新值 + 已經計算過的值

我們簡單的構造一個例子來描述一下這道題：

 對於這道題來說，剛好利用動態規劃的時間複雜度也是O（n）

動態規劃的靈魂在於，他會記錄每一次計算的結果，避免了重複計算，後面新增的資料計算，都會基於它的前一次計算結果

以此，我們對於動態規劃的使用就要基於此點

五.總結

演演算法和資料結構是相輔相成的，只有選定了資料結構，才能依據作出相應的演演算法

所以，在學演演算法前，資料結構的知識也要有

 

————————————部落格根據——浙江大學陳越老師的《資料結構》課程學習筆記