OCR 文字檢測，可微的二值化（Differentiable Binarization --- DB）

影象二值化

影象二值化（ Image Binarization），指將影象上的畫素點灰度值設為0或255,將整個影象呈現出明顯的黑白效果過程，二值影象每個畫素只有兩種取值：要麼純黑，要麼純白
影象二值化，有利於影象的進一步處理，使影象變得簡單，資料量減少（256位的灰度圖，共有256級，變成黑白影象後，只有2級），能凸顯出感興趣的目標輪廓，然後進行二值影象的處理與分析
閾值法是指選取一個數位，大於它就視為全白，小於它就視為全黑，0代表全黑，255代表全白
所有灰度大於或等於閥值的畫素，被判定為屬於特定物體，其灰度值為255表示，
否則這些畫素點被排除在物體區域以外，灰度值為0，表示背景或者例外的特體區域

OpenCV （固定伐值）

import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import cv2

# Load image
img = cv2.imread('images/006.jpg')

# Apply thresholding
binary = cv2.threshold(img, 128, 255, cv2.THRESH_BINARY)[1]

save_file = './ocr_result/binary_image.jpg'
# Save output image
cv2.imwrite(save_file, binary)

# 顯示圖片--二分值
img1 = mpimg.imread(save_file)
plt.figure(figsize=(10, 10))
plt.imshow(img1)
plt.axis('off')
plt.show()

文字檢測

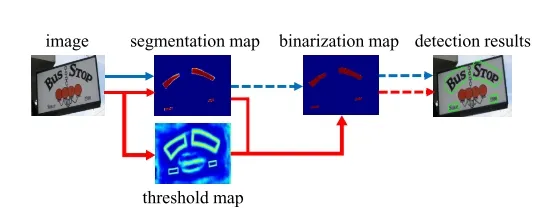
基於分割的做法（如藍色箭頭所示）：
傳統的pipeline使用固定的閾值對於分割後的熱力圖進行二值化處理【見上文】

首先，它們設定了固定的閾值，用於將分割網路生成的概率圖轉換為二進位制影象
然後，用一些啟發式技術（例如畫素聚類）用於將畫素分組為文字範例

DB的做法（如紅色箭頭所示）：
而本文提出的pipeline會將二值化操作嵌入到分割網路中進行組合優化，會生成與熱力圖對應的閾值圖，通過二者的結合生成最終的二值化操作。

在得到分割map後，與網路生成的threshold map一次聯合做可微分二值化得到二值化圖，然後再經過後處理得到最終結果。
將二值化操作插入到分段網路中以進行聯合優化，通過這種方式，可以自適應地預測影象每個位置的閾值，從而可以將畫素與前景和背景完全區分開。但是，標準二值化函數是不可微分的，因此，我們提出了一種二值化的近似函數，稱為可微分二值化（DB），當訓練時，該函數完全可微分。將一個固定的閾值訓練為一個可學習的每個位置的閾值

標籤生成

首先看label是如何生成的，網路要學習的目標gt 與 threshold map是怎樣的生成和指導網路去訓練的,知道threshold_map的label值跟gt的值，我們才能更好地去理解「可微分二值化」是如何實現的；

給定一張文字影象，其文字區域的每個多邊形由一組線段描述：

$\ G = \{S_k\}^n_{k = 1}$

其中，$G$為標註的 gt，$S$ 為gt的邊，$n$為頂點的數量 , 將$G$向內偏移$D$，形成$G_s$，在預測圖上將$G_s$內的值設定為1，$G_s$外設定為0

使用Vatti clipping algorithm (Vati 1992)縮小多邊形，對 gt 多邊形(polygon) 進行縮放；收縮偏移量（offset of shrinking）$D$ 可以通過周長 $L$ 和麵積 $A$ 計算：

$\ D = \frac {A(1-r^2)}{L}$

其中，$r$ 是縮放比例，依經驗一般取值為 0.4

這樣我們就通過 gt polygon 形成縮小版的 polygon 的gt mask圖 probability map（藍色邊界）
以同樣的 offset D 從多邊形polygon $G$ 拓展到 $G_d$ ，得到如圖中 threshold_map中的(綠色邊界)
threshold_map中由 $G_s$ 到 $G_d$ 之間形成了一個文字區域的邊界。

一組圖來視覺化影象生成的結果：

我們可以看到 probability map 的 gt 是一個完全的0，1 mask ,polygon 的縮小區域為1，其他背景區域為0；
但是在threshold_map文字邊框值並非0,1；
使用PyCharm的view array 我們能看到threshold_map中文字邊框的數值資訊：

文字最外圈邊緣為0.7，靠近中心區域是為0.3的值。（0.3-0.7為預設的閾值最大最小值）。我們可以看到文字邊界為閾值最大，然後根據文字範例邊緣距離逐漸遞減。
知道threshold_map的label值跟gt的值，我們才能更好地去理解「可微分二值化」是如何實現的；

獲取邊界框

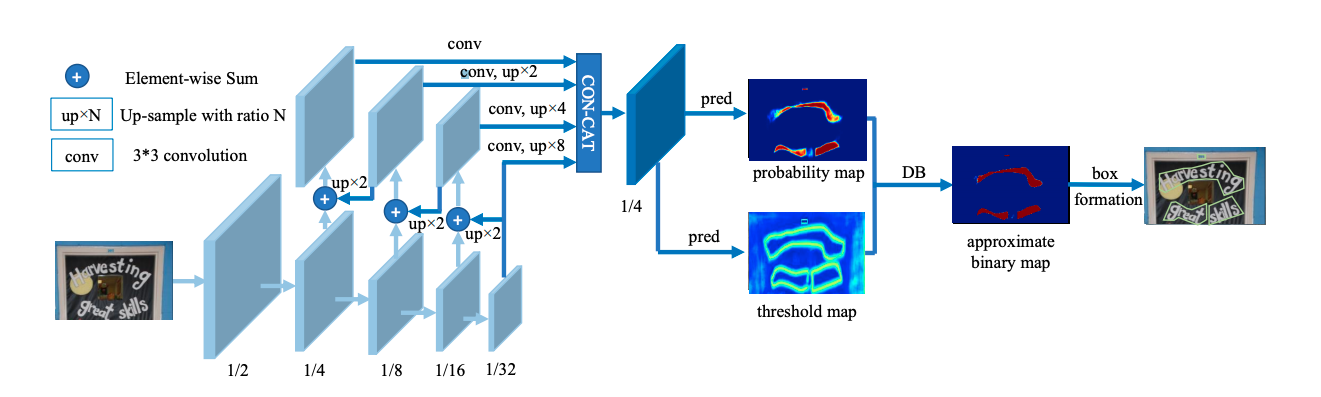
整體流程如圖所示：

backbone網路提取影象特徵
類似FPN網路結構進行影象特徵融合後得到兩個特徵圖 probability map 跟 threshold map
probability map 與threshold map 兩個特徵圖做DB差分操作得到文字區域二分圖
二分圖經過cv2 輪廓得到文字區域資訊

首先，圖片通過特徵金字塔結構的backbone，通過上取樣的方式將特徵金字塔的輸出變換為同一尺寸，並級聯(cascade)產生特徵F；然後，通過特徵圖F預測概率圖(P — probability_map)和閾值圖(T — threshold_map); 最後，通過概率圖P和閾值圖T生成近似的二值圖(B — approximate_binary_map)。

在訓練階段，監督被應用在閾值圖、概率圖和近似的二值圖上，其中後兩者共用同一個監督；在推理階段，則可以從後兩者輕鬆獲取邊界框。

可微的二值化(Differentiable binarization)

傳統的閾值分割做法為：

$\ B_{i,j} $ 代表了probability_map中第i行第j列的概率值。這樣的做法是硬性將概率大於某個固定閾值的畫素作為文字畫素，而不能將閾值作為一個可學習的引數物件（因為閾值分割沒辦法微分進行梯度回傳）

可微分的二值化公式：

首先，該公式借鑑了sigmod函數的形式（sigmod 函數本身就是將輸入對映到0~1之間），所以將概率值 $\ P_{i,j} $ 與閾值 $\ T_{i,j} $ 之間的差值作為sigmod函數的輸出，然後再經過放大係數 $k$, 將其輸出無限逼近兩個極端 0 或者1；
其中, $\hat{B}_{i,j}$ 是近似的二值化圖，$T_{i,j}$ 是閾值圖上由網路訓練時生成的值 $k$ 為放大因子，依經驗設定為 50
帶有自適應閾值的可微分二值化不僅有助於把文字區域與背景區分開，而且還能把相近的範例分離開來。

我們來根據label generation中的gt 與 threshold_map來分別計算下。經過這個可微分二值化的sigmod函數後，各個區域的畫素值會變成什麼樣子：
文字範例中心區域畫素：

probability map 的gt為 1
threshold map的gt值為0.3

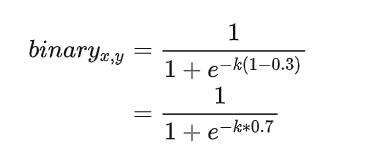
如果不經過放大係數K的放大，那麼區域正中心的畫素如上圖所示經過sigmod函數後趨向於0.6左右的值。但是經過放大係數k後，會往右傾向於1。

文字範例邊緣區域畫素：

probability map 的gt為 1
threshold map的gt值為0.7

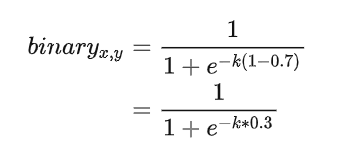
如果不經過放大係數K的放大，那麼區域正中心的畫素如上圖所示經過sigmod函數後趨向於0.5左右的值。但是經過放大係數k後，會往右傾向於1。

文字範例外的畫素：

probability map 的gt為 0
threshold map的gt值為0.3

經過放大係數k後，啟用值會無限趨近於0；從而實現二值化效果。
解釋了DB利用類似sigmod的函數是如何實現二值化的效果，那麼我們來看其梯度的學習性：

傳統二值化是一個分段函數，如下圖所示：

SB(Standard Binarization)其梯度在0值被截斷無法進行有效地回傳。
DB(Differentiable Binarization)是一個可微分的曲線，可以利用訓練資料+優化器的形式進行資料驅動的學習優化。

我們來看其導數公式，假設 $l_+$ 代表了正樣本， $l_-$ 代表了負樣本，則：

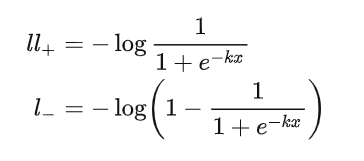
根據鏈式法則我們可以計算其loss梯度

百度paddle中提供的介面可以實現下面的效果：