技術文章 » LeetCode 周賽 344（2023/05/07）手寫遞迴函數的固定套路

LeetCode 周賽 344（2023/05/07）手寫遞迴函數的固定套路

2023-05-08 06:01:05

本文已收錄到 AndroidFamily，技術和職場問題，請關注公眾號 [彭旭銳] 提問。

大家好，我是小彭。

今天下午有力扣杯戰隊賽，不知道官方是不是故意調低早上週賽難度給選手們練練手。

周賽概覽

T1. 找出不同元素數目差陣列（Easy）

標籤：模擬、計數、雜湊表

T2. 頻率跟蹤器（Medium）

標籤：模擬、計數、雜湊表、設計

T3. 有相同顏色的相鄰元素數目（Medium）

標籤：模擬、計數、貪心

T4. 使二元樹所有路徑值相等的最小代價（Medium）

標籤：二元樹、DFS、貪心

T1. 找出不同元素數目差陣列（Easy）

https://leetcode.cn/problems/find-the-distinct-difference-array/

題解（前字尾分解）

  • 問題目標：求每個位置字首中不同元素個數和字尾不同元素個數的差值；
  • 觀察資料：存在重複數；
  • 解決手段：我們可以計算使用兩個雜湊表計算字首和字尾中不同元素的差值。考慮到字首和字尾的數值沒有依賴關係，只不過字尾是負權，字首是正權。那麼，我們可以在第一次掃描時將字尾的負權值記錄到結果陣列中，在第二次掃描時將正權值記錄到結果陣列中，就可以優化一個雜湊表空間。

寫法 1：

class Solution {
    fun distinctDifferenceArray(nums: IntArray): IntArray {
        val n = nums.size
        val ret = IntArray(n)
        val leftCnts = HashMap<Int, Int>()
        val rightCnts = HashMap<Int, Int>()

        for (e in nums) {
            rightCnts[e] = rightCnts.getOrDefault(e, 0) + 1
        }

        for (i in nums.indices) {
            val e = nums[i]
            leftCnts[e] = leftCnts.getOrDefault(e, 0) + 1
            if (rightCnts[e]!! > 1) rightCnts[e] = rightCnts[e]!! - 1 else rightCnts.remove(e)
            ret[i] = leftCnts.size - rightCnts.size
        }
        return ret
    }
}

寫法 2：

class Solution {
    fun distinctDifferenceArray(nums: IntArray): IntArray {
        val n = nums.size
        val ret = IntArray(n)
        val set = HashSet<Int>()

        // 字尾
        for (i in nums.size - 1 downTo 0) {
            ret[i] = -set.size
            set.add(nums[i])
        }

        set.clear()

        // 字首
        for (i in nums.indices) {
            set.add(nums[i])
            ret[i] += set.size
        }
        return ret
    }
}

複雜度分析：

  • 時間複雜度：$O(n)$ 其中 n 為 nums 陣列的長度；
  • 空間複雜度：$O(n)$ 雜湊表空間。

T2. 頻率跟蹤器（Medium）

https://leetcode.cn/problems/frequency-tracker/

題解（雜湊表）

簡單設計題，使用一個雜湊表記錄數位出現次數，再使用另一個雜湊表記錄出現次數的出現次數：

class FrequencyTracker() {

    // 計數
    private val cnts = HashMap<Int, Int>()

    // 頻率計數
    private val freqs = HashMap<Int, Int>()

    fun add(number: Int) {
        // 舊計數
        val oldCnt = cnts.getOrDefault(number, 0)
        // 增加計數
        cnts[number] = oldCnt + 1
        // 減少舊頻率計數
        if (freqs.getOrDefault(oldCnt, 0) > 0) // 容錯
            freqs[oldCnt] = freqs[oldCnt]!! - 1
        // 增加新頻率計數
        freqs[oldCnt + 1] = freqs.getOrDefault(oldCnt + 1, 0) + 1
    }

    fun deleteOne(number: Int) {
        // 未包含
        if (!cnts.contains(number)) return
        // 減少計數
        val oldCnt = cnts[number]!!
        if (0 == oldCnt - 1) cnts.remove(number) else cnts[number] = oldCnt - 1
        // 減少舊頻率計數
        freqs[oldCnt] = freqs.getOrDefault(oldCnt, 0) - 1
        // 增加新頻率計數
        freqs[oldCnt - 1] = freqs.getOrDefault(oldCnt - 1, 0) + 1
    }

    fun hasFrequency(frequency: Int): Boolean {
        // O(1) 
        return freqs.getOrDefault(frequency, 0) > 0
    }
}

複雜度分析：

  • 時間複雜度：$O(1)$ 每個操作的時間複雜度都是 $O(1)$；
  • 空間複雜度：$O(q)$ 取決於增加的次數 $q$。

T3. 有相同顏色的相鄰元素數目（Medium）

https://leetcode.cn/problems/number-of-adjacent-elements-with-the-same-color/description/

題目描述

給你一個下標從 0 開始、長度為 n 的陣列 nums 。一開始，所有元素都是 未染色 （值為 0 ）的。

給你一個二維整數陣列 queries ，其中 queries[i] = [indexi, colori] 。

對於每個操作，你需要將陣列 nums 中下標為 indexi 的格子染色為 colori 。

請你返回一個長度與 queries 相等的陣列 **answer **，其中 **answer[i]是前 i 個操作 之後 ，相鄰元素顏色相同的數目。

更正式的，answer[i] 是執行完前 i 個操作後，0 <= j < n - 1 的下標 j 中，滿足 nums[j] == nums[j + 1] 且 nums[j] != 0 的數目。

範例 1：

輸入：n = 4, queries = [[0,2],[1,2],[3,1],[1,1],[2,1]]
輸出：[0,1,1,0,2]
解釋：一開始陣列 nums = [0,0,0,0] ，0 表示陣列中還沒染色的元素。
- 第 1 個操作後，nums = [2,0,0,0] 。相鄰元素顏色相同的數目為 0 。
- 第 2 個操作後，nums = [2,2,0,0] 。相鄰元素顏色相同的數目為 1 。
- 第 3 個操作後，nums = [2,2,0,1] 。相鄰元素顏色相同的數目為 1 。
- 第 4 個操作後，nums = [2,1,0,1] 。相鄰元素顏色相同的數目為 0 。
- 第 5 個操作後，nums = [2,1,1,1] 。相鄰元素顏色相同的數目為 2 。

範例 2：

輸入：n = 1, queries = [[0,100000]]
輸出：[0]
解釋：一開始陣列 nums = [0] ，0 表示陣列中還沒染色的元素。
- 第 1 個操作後，nums = [100000] 。相鄰元素顏色相同的數目為 0 。

提示：

  • 1 <= n <= 105
  • 1 <= queries.length <= 105
  • queries[i].length == 2
  • 0 <= indexi <= n - 1
  • 1 <= colori <= 105

問題結構化

1、概括問題目標

計算每次塗色後相鄰顏色的數目個數（與前一個位置顏色相同）。

2、觀察問題資料

  • 資料量：查詢操作的次數是 10^5，因此每次查詢操作的時間複雜度不能高於 O(n)。

3、具體化解決手段

  • 手段 1（暴力列舉）：塗色執行一次線性掃描，計算與前一個位置顏色相同的元素個數；
  • 手段 2（列舉優化）：由於每次操作最多隻會影響 (i - 1, i) 與 (i, i + 1) 兩個數對的顏色關係，因此我們沒有必要列舉整個陣列。

題解一（暴力列舉 · TLE）

class Solution {
    fun colorTheArray(n: Int, queries: Array<IntArray>): IntArray {
        // 只觀察 (i - 1, i) 與 (i, i + 1) 兩個數對
        if (n <= 0) return intArrayOf(0) // 容錯

        val colors = IntArray(n)
        val ret = IntArray(queries.size)

        for (i in queries.indices) {
            val j = queries[i][0]
            val color = queries[i][1]
            if (j < 0 || j >= n) continue // 容錯
            colors[j] = color
            for (j in 1 until n) {
                if (0 != colors[j] && colors[j] == colors[j - 1]) ret[i] ++
            }
        }
        return ret
    }
}

複雜度分析：

  • 時間複雜度：$O(n^2)$ 每個操作的時間複雜度都是 O(n)；
  • 空間複雜度：$O(n)$ 顏色陣列空間。

題解二（列舉優化）

class Solution {
    fun colorTheArray(n: Int, queries: Array<IntArray>): IntArray {
        // 只觀察 (i - 1, i) 與 (i, i + 1) 兩個數對
        if (n <= 0) return intArrayOf(0) // 容錯

        val colors = IntArray(n)
        val ret = IntArray(queries.size)

        // 計數
        var cnt = 0
        for (i in queries.indices) {
            val j = queries[i][0]
            val color = queries[i][1]
            if (j < 0 || j >= n) continue // 容錯
            // 消除舊顏色的影響
            if (colors[j] != 0 && j > 0 && colors[j - 1] == colors[j]) cnt--
            // 增加新顏色的影響
            if (colors[j] != 0 && j < n - 1 && colors[j] == colors[j + 1]) cnt--
            if (color != 0) { // 容錯
                colors[j] = color
                if (j > 0 && colors[j - 1] == colors[j]) cnt++
                if (j < n - 1 && colors[j] == colors[j + 1]) cnt++
            }
            ret[i] = cnt
        }
        return ret
    }
}

複雜度分析：

  • 時間複雜度：$O(n)$ 每個操作的時間複雜度都是 O(1)；
  • 空間複雜度：$O(n)$ 顏色陣列空間。

相似題目：

T4. 使二元樹所有路徑值相等的最小代價（Medium）

https://leetcode.cn/problems/make-costs-of-paths-equal-in-a-binary-tree/

問題描述

給你一個整數 n 表示一棵 滿二元樹 裡面節點的數目，節點編號從 1 到 n 。根節點編號為 1 ，樹中每個非葉子節點 i 都有兩個孩子，分別是左孩子 2 * i 和右孩子 2 * i + 1 。

樹中每個節點都有一個值，用下標從 0 開始、長度為 n 的整數陣列 cost 表示，其中 cost[i] 是第 i + 1 個節點的值。每次操作，你可以將樹中 任意 節點的值 增加 1 。你可以執行操作 任意 次。

你的目標是讓根到每一個 葉子結點 的路徑值相等。請你返回 最少 需要執行增加操作多少次。

注意：

  • 滿二元樹 指的是一棵樹，它滿足樹中除了葉子節點外每個節點都恰好有 2 個節點，且所有葉子節點距離根節點距離相同。
  • 路徑值 指的是路徑上所有節點的值之和。

範例 1：

輸入：n = 7, cost = [1,5,2,2,3,3,1]
輸出：6
解釋：我們執行以下的增加操作：
- 將節點 4 的值增加一次。
- 將節點 3 的值增加三次。
- 將節點 7 的值增加兩次。
從根到葉子的每一條路徑值都為 9 。
總共增加次數為 1 + 3 + 2 = 6 。
這是最小的答案。

範例 2：

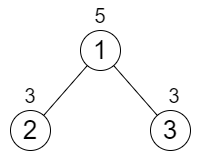
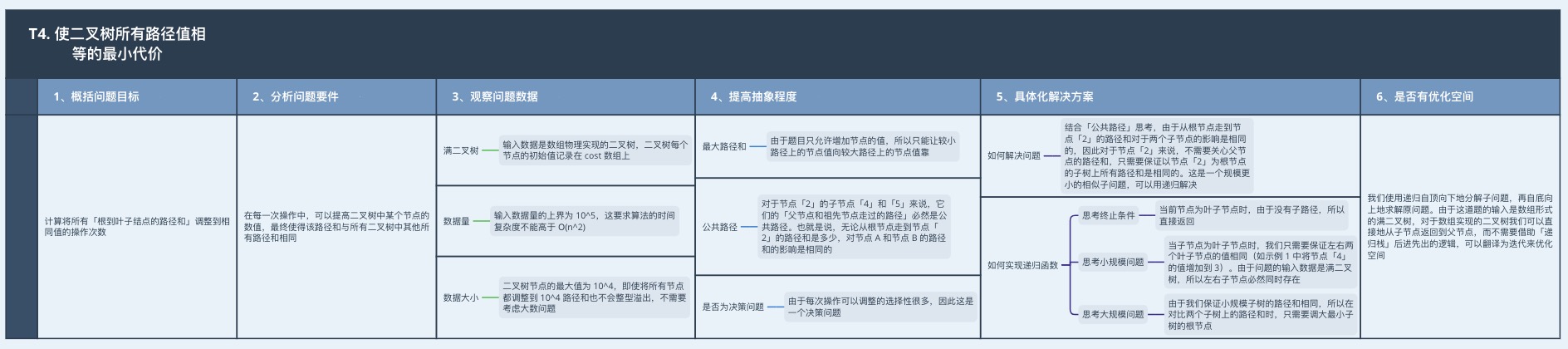
輸入：n = 3, cost = [5,3,3]
輸出：0
解釋：兩條路徑已經有相等的路徑值，所以不需要執行任何增加操作。

提示：

  • 3 <= n <= 105
  • n + 1 是 2 的冪
  • cost.length == n
  • 1 <= cost[i] <= 104

問題結構化

1、概括問題目標

計算將所有「根到葉子結點的路徑和」調整到相同值的操作次數。

2、分析問題要件

在每一次操作中，可以提高二元樹中某個節點的數值，最終使得該路徑和與所有二元樹中其他所有路徑和相同。

3、觀察問題資料

  • 滿二元樹：輸入資料是陣列物理實現的二元樹，二元樹每個節點的初始值記錄在 cost 陣列上；
  • 資料量：輸入資料量的上界為 10^5，這要求演演算法的時間複雜度不能高於 O(n^2)；
  • 資料大小：二元樹節點的最大值為 10^4，即使將所有節點都調整到 10^4 路徑和也不會整型溢位，不需要考慮大數問題。

4、提高抽象程度

  • 最大路徑和：由於題目只允許增加節點的值，所以只能讓較小路徑上的節點值向較大路徑上的節點值靠；
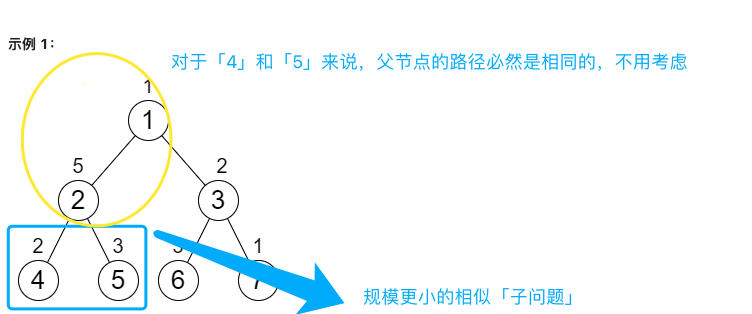
  • 公共路徑：對於節點「2」的子節點「4」和「5」來說，它們的「父節點和祖先節點走過的路徑」必然是公共路徑。也就是說，無論從根節點走到節點「2」的路徑和是多少，對節點 A 和節點 B 的路徑和的影響是相同的。
  • 是否為決策問題：由於每次操作可以調整的選擇性很多，因此這是一個決策問題。

5、具體化解決方案

如何解決問題？

結合「公共路徑」思考，由於從根節點走到節點「2」的路徑和對於兩個子節點的影響是相同的，因此對於節點「2」來說，不需要關心父節點的路徑和，只需要保證以節點「2」為根節點的子樹上所有路徑和是相同的。這是一個規模更小的相似子問題，可以用遞迴解決。

示意圖

如何實現遞迴函數？

  • 思考終止條件：當前節點為葉子節點時，由於沒有子路徑，所以直接返回；
  • 思考小規模問題：當子節點為葉子節點時，我們只需要保證左右兩個葉子節點的值相同（如範例 1 中將節點「4」的值增加到 3）。由於問題的輸入資料是滿二元樹，所以左右子節點必然同時存在；
  • 思考大規模問題：由於我們保證小規模子樹的路徑和相同，所以在對比兩個子樹上的路徑和時，只需要調大最小子樹的根節點。

至此，我們的遞迴函數框架確定：

全域性變數 int ret
// 返回值：調整後的子樹和
fun dfs (i) : Int {
		val sumL = dfs(L)
		val sumR = dfs(R)
		ret += max(sumL, sumR) - min(sumL, sumR) 
		return cost[i] + max(sumL, sumR)
}

6、是否有優化空間

我們使用遞迴自頂向下地分解子問題，再自底向上地求解原問題。由於這道題的輸入是陣列形式的滿二元樹，對於陣列實現的二元樹我們可以直接地從子節點返回到父節點，而不需要藉助「遞迴棧」後進先出的邏輯，可以翻譯為迭代來優化空間。

7、答疑

雖然我們保證子樹上的子路徑是相同的，但是如何保證最終所有子路徑都和「最大路徑和」相同？

由於我們不斷地將左右子樹的路徑和向較大的路徑和對齊，因此最終一定會將所有路徑對齊到最大路徑和。

為什麼演演算法的操作次數是最少的？

首先，由於左右子樹存在「公共路徑」，因此必須把左右子樹的子路徑和調整到相同數值，才能保證最終所有子路徑和的長度相同。

其次，當在大規模子樹中需要增大路徑和時，在父節點操作可以同時作用於左右子路徑，因此在父節點操作可以節省操作次數，每個子樹只關心影響當前子樹問題合法性的因素。

題解一（DFS）

根據「問題結構化」分析的遞迴虛擬碼實現：

class Solution {

    private var ret = 0

    fun minIncrements(n: Int, cost: IntArray): Int {
        dfs(n, cost, 1)
        return ret
    }

    // i : base 1
    // cost : base 0
    // return: 調整後的子路徑和
    private fun dfs(n: Int, cost: IntArray, i: Int): Int {
        // 終止條件
        if (i > n / 2) return cost[i - 1] // 最後一層是葉子節點
        // 子問題
        val leftSum = dfs(n, cost, i * 2)
        val rightSum = dfs(n, cost, i * 2 + 1)
        // 向較大的子路徑對齊
        ret += Math.max(leftSum, rightSum) - Math.min(leftSum, rightSum)
        return cost[i - 1] + Math.max(leftSum, rightSum)
    }
}

複雜度分析：

  • 時間複雜度：$O(n)$ 其中 n 為 節點數，每個節點最多存取 1 次；
  • 空間複雜度：$O(lgn)$ 遞迴棧空間，由於輸入是滿二元樹，所以遞迴棧深度最大為 lgn。

題解二（迭代）

由於輸入資料是滿二元樹，而且是以陣列的形式提供，因此我們可以跳過遞迴分解子問題的過程，直接自底向上合併子問題：

class Solution {
    fun minIncrements(n: Int, cost: IntArray): Int {
        var ret = 0
        // 從葉子的上一層開始
        for (i in n / 2 downTo 1) {
            ret += Math.abs(cost[i * 2 - 1] - cost[i * 2])
            // 藉助 cost 陣列記錄子樹的子路徑和
            cost[i - 1] += Math.max(cost[i * 2 - 1], cost[i * 2])
        }
        return ret
    }
}

複雜度分析：

  • 時間複雜度：$O(n)$ 其中 n 為 節點數，每個節點最多存取 1 次；
  • 空間複雜度：$O(1)$ 僅使用常數級別空間。

往期回顧