「學習筆記」雙連通分量、割點與橋
文章圖片全部來自 Oi-wiki,部分圖片加以修改
前面我們在學 tarjan 演演算法時,提到過強連通分量,即有向圖上的環,那麼無向圖上是否也有強連通分量呢?很遺憾,沒有
但是,無向圖有雙連通分量!分為點雙連通和邊雙連通(下面簡稱點雙和邊雙)。
邊雙連通分量
概念
在一張聯通的無向圖中,對於兩個點 \(x\) 和 \(y\),刪去圖上的任意一條邊,兩個點始終保持聯通,則這兩個點是邊雙連通。
邊雙連通分量,即極大邊雙連通子圖,邊雙連通分量中的任意兩點都是邊雙連通的,且如果加入一個不屬於該子圖的點,都會導致這個圖不再滿足兩兩之間邊雙的性質。
在無向圖中。刪掉一條邊,導致兩個圖不連通了,這條邊就是割邊,也叫做橋。
邊雙連通具有傳遞性,即如果 \(x\) 與 \(y\) 邊雙連通,\(y\) 與 \(z\) 邊雙連通,則 \(x\) 與 \(z\) 也邊雙連通。
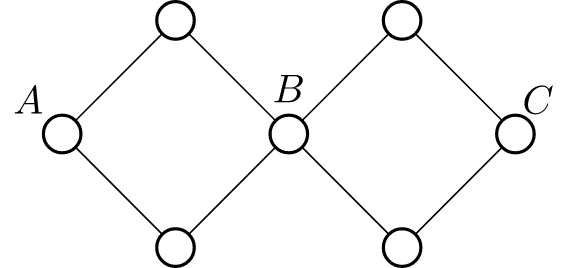
如圖,在這張圖中,\(A\) 與 \(B\) 邊雙連通,\(B\) 與 \(C\) 邊雙連通,根據傳遞性,\(A\) 與 \(C\) 邊雙連通。(即使不跟據傳遞性,他們也的確是邊雙連通)
找橋的過程
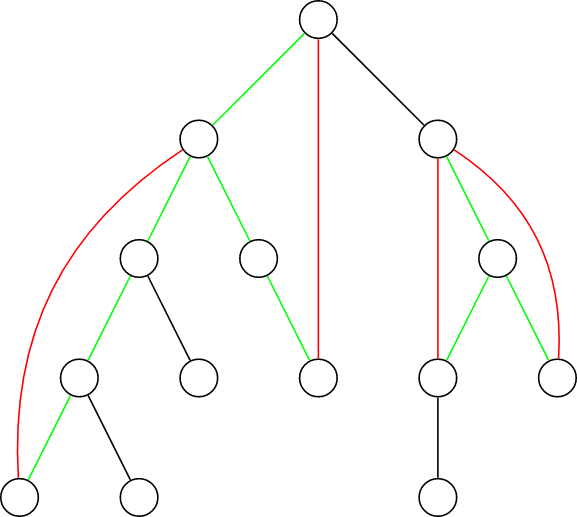
如圖,綠色的邊和黑色的邊都是樹邊,紅色的邊是返祖邊。
我們發現,每一條返祖邊都對應著一條樹上的簡單路徑,即覆蓋了樹上的一些邊,覆蓋了的邊我們用綠邊表示,黑色的邊沒有被覆蓋。我們如果刪去返祖邊或者任意一條綠邊,都不會影響圖的連通性(如果刪掉返祖邊就從綠邊走,如果刪掉綠邊就從返祖邊走),但是,如果我們刪掉黑邊,那麼整個圖就會被一分為二,不再保持聯通,這些黑色的邊就是橋,同時返祖邊和綠邊一定不是橋。
這樣,我們只要找到所有的橋,就能確定邊雙連通分量了。
找邊雙連通分量,我們可以用 tarjan 演演算法。
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ tim; // 打上時間戳
for (int i = h[u], v; i; i = e[i].nxt) {
v = e[i].v;
if ((i ^ 1) == fa) continue;
if (!dfn[v]) { // 如果這個點從未被搜過
tarjan(v, i); // 繼續往下搜
low[u] = min(low[u], low[v]); // 正常更新 low 值
if (low[v] > dfn[u]) { // 如果 v 點無法通過返祖邊向上返回到 u 點即往上
e[i].ok = e[i ^ 1].ok = 1; // 那麼這條邊就是橋
}
// 不理解的話可以想一想,v 點不管怎麼向上都不能到達 u 點即更靠上的位置,那 u -> v 這條邊就沒有被返祖邊覆蓋,它就是橋
}
else { // 如果這個點已經被搜過了(說明這條邊是返祖邊)
low[u] = min(low[u], dfn[v]); // 更新 low 值(比較的是 dfn[v],不是 low[v])
}
}
}
找邊雙連通分量
有兩種方式,像找強連通分量那樣用一個棧,或者標記橋之後再 dfs。
洛谷模板題測試,用棧比標記橋更快一些。
- 用棧找雙連通分量
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ tim;
sta.push_back(u);
for (auto [v, i] : son[u]) {
if (i == fa) continue;
if (! dfn[v]) {
tarjan(v, i);
low[u] = min(low[u], low[v]);
}
else {
low[u] = min(low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
ans[++ dcc].push_back(u);
while (sta.back() != u) {
ans[dcc].push_back(sta.back());
sta.pop_back();
}
sta.pop_back();
}
}
- 標記橋,dfs。
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ tim;
for (auto [v, i] : son[u]) {
if (i == fa) continue;
if (! dfn[v]) {
tarjan(v, i);
low[u] = min(low[u], low[v]);
if (low[v] > dfn[u]) {
ok[i] = 1;
}
}
else {
low[u] = min(low[u], dfn[v]);
}
}
}
void dfs(int u) { // dfn 要清零,你也可以再開一個陣列
ans[dcc].push_back(u);
dfn[u] = 1;
for (auto [v, i] : son[u]) {
if (dfn[v] || ok[i]) continue;
dfs(v);
}
}
點雙連通分量
概念
在一張聯通的無向圖中,對於兩個點 \(x\) 和 \(y\),刪去圖上的任意一個點(不能刪去 \(x\) 和 \(y\)),兩個點始終保持聯通,則這兩個點是點雙連通。
刪去一個點,會刪掉這個點以及這個點所連線的所有的邊,所以橋連線的兩個點都是割點。
點雙連通分量,即極大點雙連通子圖,點雙連通分量中的任意兩點都是點雙連通的,且如果加入一個不屬於該子圖的點,都會導致這個圖不再滿足兩兩之間點雙的性質。
在無向圖中。刪掉一個點,導致兩個圖不連通了,這個點就是割點。
點雙連通沒有傳遞性,即如果 \(x\) 和 \(y\) 點雙聯通,\(y\) 和 \(z\) 點雙聯通,\(x\) 和 \(z\) 不一定點雙聯通。
舉個例子。
\(A\) 與 \(B\) 點雙連通,\(B\) 與 \(C\) 點雙連通,但是 \(A\) 與 \(C\) 並不是點雙連通。(割點為 \(B\))
過程

如圖,黑色的邊是樹邊,紅色的邊是返祖邊,每一條返祖邊對應著一條簡單路徑。
現在,我們將每一條邊看作是一個點,即圖上藍色的點,返祖邊所覆蓋的簡單路徑上的邊都連上邊,即圖上的藍邊。
這樣,要判斷點是否為割點,只要判斷這個點連出去的邊是否在一個連通分量裡,都在一個連通分量裡,就不是割點,否則就是割點
這裡還有另一種做法。
對於某個頂點 \(u\),如果存在至少一個頂點 \(v\),使得 low[v] \(\geq\) dfn[u],即不能回到祖先,那麼 \(u\) 點為割點。
但這個做法唯獨不適用於搜尋樹的起始點,即搜尋樹的根,如果根只有一個子樹,那我們把根節點刪去,對圖的連通性不會有任何影響,即根節點不是割點,如果根節點有著至少兩個子樹,那麼根節點就是割點。
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ cnt;
int son = 0;
for (int i = h[u], v; i; i = e[i].nxt) {
v = e[i].v;
if (v == fa) continue;
if (!dfn[v]) {
++ son;
tarjan(v, u);
low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u]) {
ok[u] = 1;
++ dcc;
}
}
else {
low[u] = min(low[u], dfn[v]);
}
}
if (fa == 0 && son < 2) ok[u] = 0;
}
應用
在題目中,橋一般出現在「給定一張無向圖,問是否有一種方案,能給定向,同時保證每個點都能走到」這樣類似的題目上,在這道題中,有橋就沒有可行方案,倘若要輸出方案,我們可以利用 dfs 生成樹。
由於邊雙比點雙有著更好的性質,所以一般題目都是有關邊雙的。
關於用 vector 來寫 tarjan
優點:動態空間,方便。
缺點:慢!
上面的程式碼我們也看到了,有些題目有重邊,用一般的 vector 存圖方式判斷是否走過重邊,這裡有一個方式可以實現用 vector 來找重邊,那就是將 vector 的變數型別改成 pair,第一個元素存到達的節點,第二個元素存這條邊的編號,如果不保險可以再開一個 vector 、結構體或兩個陣列來存第 \(i\) 條邊的兩個端點的編號,像這樣。
e.push_back({0, 0});
for (int i = 1, x, y; i <= m; ++ i) {
scanf("%d%d", &x, &y);
son[x].push_back({y, i});
son[y].push_back({x, i});
e.push_back({x, y});
}
這樣,我們在 tarjan 判重邊的的過程中可以直接判斷編號了。
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ tim;
for (auto [v, i] : son[u]) {
if (i == fa) continue;
if (! dfn[v]) {
tarjan(v, i);
low[u] = min(low[v], low[u]);
if (low[v] > dfn[u]) {
ok[i] = 1;
}
}
else {
low[u] = min(low[u], dfn[v]);
}
}
}
對於找割點,我們直接用 vector 就行了,這裡不存在任何限制,就是會慢。
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ cnt;
st[++ top] = u;
int ch = 0;
for (int v : son[u]) {
if (v == fa) continue;
if (!dfn[v]) {
++ ch;
tarjan(v, u);
low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u]) {
ok[u] = 1;
++ dcc;
while (st[top + 1] != v) {
ans[dcc].push_back(st[top --]);
}
ans[dcc].push_back(u);
}
}
else {
low[u] = min(low[u], dfn[v]);
}
}
if (fa == 0 && ch == 0) ans[++ dcc].push_back(u);
if (fa == 0 && ch < 2) ok[u] = 0;
}
題目
都是來源於洛谷的模板題
P8436 【模板】邊雙連通分量
- 直接用棧來找邊雙。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 5e5 + 5;
const int M = 2e6 + 5;
int n, m, cnt = 1, tim, top, dcc;
int h[N], dfn[N], low[N];
bool ok[M];
vector<pii> son[N];
vector<int> ans[N], sta;
struct edge {
int v, nxt;
bool ok;
} e[M << 1];
void add(int u, int v) {
e[++ cnt].nxt = h[u];
e[h[u] = cnt].v = v;
}
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ tim;
sta.push_back(u);
for (auto [v, i] : son[u]) {
if (i == fa) continue;
if (! dfn[v]) {
tarjan(v, i);
low[u] = min(low[u], low[v]);
}
else {
low[u] = min(low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
ans[++ dcc].push_back(u);
while (sta.back() != u) {
ans[dcc].push_back(sta.back());
sta.pop_back();
}
sta.pop_back();
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1, x, y; i <= m; ++ i) {
scanf("%d%d", &x, &y);
son[x].push_back({y, i});
son[y].push_back({x, i});
}
for (int i = 1; i <= n; ++ i) {
if (!dfn[i]) {
tarjan(i, 0);
}
}
printf("%d\n", dcc);
for (int i = 1; i <= dcc; ++ i) {
int siz = ans[i].size();
printf("%d ", siz);
for (int j : ans[i]) {
printf("%d ", j);
}
putchar('\n');
}
return 0;
}
- 標記橋,通過 dfs 來找邊雙。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 5e5 + 5;
const int M = 2e6 + 5;
int n, m, cnt = 1, tim, top, dcc;
int h[N], dfn[N], low[N];
bool ok[M];
vector<int> ans[N];
vector<pii> son[N];
struct edge {
int v, nxt;
bool ok;
} e[M << 1];
void add(int u, int v) {
e[++ cnt].nxt = h[u];
e[h[u] = cnt].v = v;
}
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ tim;
for (auto [v, i] : son[u]) {
if (i == fa) continue;
if (! dfn[v]) {
tarjan(v, i);
low[u] = min(low[u], low[v]);
if (low[v] > dfn[u]) {
ok[i] = 1;
}
}
else {
low[u] = min(low[u], dfn[v]);
}
}
}
void dfs(int u) {
ans[dcc].push_back(u);
dfn[u] = 1;
for (auto [v, i] : son[u]) {
if (dfn[v] || ok[i]) continue;
dfs(v);
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1, x, y; i <= m; ++ i) {
scanf("%d%d", &x, &y);
son[x].push_back({y, i});
son[y].push_back({x, i});
}
for (int i = 1; i <= n; ++ i) {
if (!dfn[i]) {
tarjan(i, 0);
}
}
memset(dfn, 0, sizeof dfn);
for (int i = 1; i <= n; ++ i) {
if (!dfn[i]) {
++ dcc;
dfs(i);
}
}
printf("%d\n", dcc);
for (int i = 1; i <= dcc; ++ i) {
int siz = ans[i].size();
printf("%d ", siz);
for (int j : ans[i]) {
printf("%d ", j);
}
putchar('\n');
}
return 0;
}
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5e5 + 5;
const int M = 2e6 + 5;
int n, m, cnt, top, dcc;
int h[N], dfn[N], low[N], st[N];
bool ok[N];
vector<int> son[N], ans[N];
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ cnt;
st[++ top] = u;
int ch = 0;
for (int v : son[u]) {
if (v == fa) continue;
if (!dfn[v]) {
++ ch;
tarjan(v, u);
low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u]) {
ok[u] = 1;
++ dcc;
while (st[top + 1] != v) {
ans[dcc].push_back(st[top --]);
}
ans[dcc].push_back(u);
}
}
else {
low[u] = min(low[u], dfn[v]);
}
}
if (fa == 0 && ch == 0) ans[++ dcc].push_back(u);
if (fa == 0 && ch < 2) ok[u] = 0;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1, x, y; i <= m; ++ i) {
scanf("%d%d", &x, &y);
son[x].push_back(y);
son[y].push_back(x);
}
cnt = 0;
for (int i = 1; i <= n; ++ i) {
if (!dfn[i]) {
top = 0;
tarjan(i, 0);
}
}
printf("%d\n", dcc);
for (int i = 1; i <= dcc; ++ i) {
printf("%d ", (int)ans[i].size());
for (int j : ans[i]) {
printf("%d ", j);
}
putchar('\n');
}
return 0;
}