LeetCode 周賽 343（2023/04/30）結合「下一個排列」的貪心構造問題

本文已收錄到 AndroidFamily，技術和職場問題，請關注公眾號 [彭旭銳] 提問。

大家好，我是小彭。

今天是五一假期的第二天，打周賽的人數比前一天的雙週賽多了，難道大家都只玩一天嗎？這場周賽是 LeetCode 第 343 場單週賽，如果不考慮第一題擺爛的翻譯，整體題目質量還是很不錯噠。

往期回顧：LeetCode 雙週賽第 103 場 · 區間求和的樹狀陣列經典應用

周賽概覽

Q1. 保齡球遊戲的獲勝者（Easy）

標籤：陣列、模擬、計數

Q2. 找出疊塗元素（Medium）

標籤：矩陣、雜湊表、計數

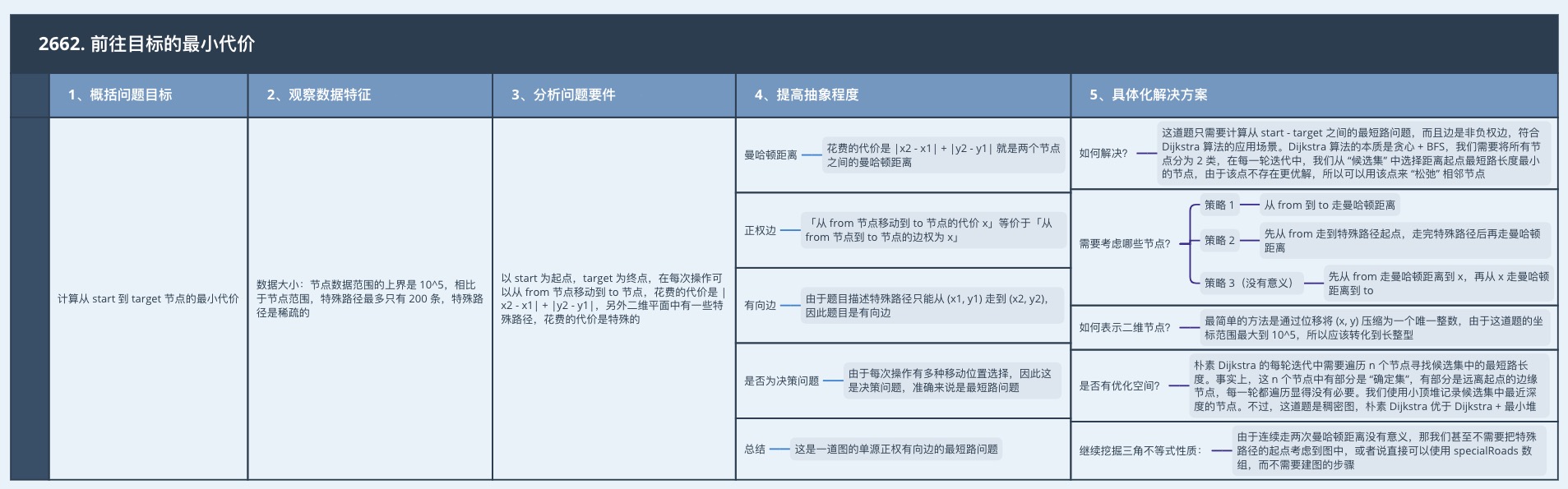
Q3. 前往目標的最小代價（Medium）

標籤：最短路、Dijkstra、最小堆

Q4. 字典序最小的美麗字串（Hard）

標籤：貪心、構造

---

Q1. 保齡球遊戲的獲勝者（Easy）

https://leetcode.cn/problems/determine-the-winner-of-a-bowling-game/

題目描述

給你兩個下標從 0 開始的整數陣列 player1 和 player2 ，分別表示玩家 1 和玩家 2 擊中的瓶數。

保齡球比賽由 n 輪組成，每輪的瓶數恰好為 10 。

假設玩家在第 i 輪中擊中 xi 個瓶子。玩家第 i 輪的價值為：

• 如果玩家在前兩輪中擊中了 10 個瓶子，則為 2xi 。
• 否則，為 xi 。

玩家的得分是其 n 輪價值的總和。

返回

• 如果玩家 1 的得分高於玩家 2 的得分，則為 1 ；
• 如果玩家 2 的得分高於玩家 1 的得分，則為 2 ；
• 如果平局，則為 0 。

範例 1：

輸入：player1 = [4,10,7,9], player2 = [6,5,2,3]
輸出：1
解釋：player1 的得分是 4 + 10 + 2*7 + 2*9 = 46 。
player2 的得分是 6 + 5 + 2 + 3 = 16 。
player1 的得分高於 player2 的得分，所以 play1 在比賽中獲勝，答案為 1 。

範例 2：

輸入：player1 = [3,5,7,6], player2 = [8,10,10,2]
輸出：2
解釋：player1 的得分是 3 + 5 + 7 + 6 = 21 。
player2 的得分是 8 + 10 + 2*10 + 2*2 = 42 。
player2 的得分高於 player1 的得分，所以 play2 在比賽中獲勝，答案為 2 。

範例 3：

輸入：player1 = [2,3], player2 = [4,1]
輸出：0
解釋：player1 的得分是 2 + 3 = 5 。
player2 的得分是 4 + 1 = 5 。
player1 的得分等於 player2 的得分，所以這一場比賽平局，答案為 0 。

提示：

• n == player1.length == player2.length
• 1 <= n <= 1000
• 0 <= player1[i], player2[i] <= 10

題解（模擬）

簡單模擬題，但題目描述的中文翻譯有歧義，而且不能根據範例區分出來：

• 理解 1：只要最開始的兩輪中擊中了 10 個瓶子，那麼後續得分加倍；
• 理解 2：任意輪的前兩輪中擊中了 10 個瓶子，那麼該輪得分加倍。

按照理解 2 模擬即可：

class Solution {
    fun isWinner(player1: IntArray, player2: IntArray): Int {
        var cnt1 = 0
        var cnt2 = 0
        for (i in player1.indices) {
            val mul1 = player1.slice(Math.max(0, i - 2) until i).any { it == 10 }
            val mul2 = player2.slice(Math.max(0, i - 2) until i).any { it == 10 }

            cnt1 += if (mul1) 2 * player1[i] else player1[i]
            cnt2 += if (mul2) 2 * player2[i] else player2[i]
        }
        return if (cnt1 == cnt2) 0 else if (cnt1 > cnt2) 1 else 2
    }
}

複雜度分析：

• 時間複雜度：$O(n)$ 其中 n 是 player1 陣列的長度；
• 空間複雜度：$O(1)$ 僅使用常數級別空間。

---

Q2. 找出疊塗元素（Medium）

https://leetcode.cn/problems/first-completely-painted-row-or-column/

題目描述

給你一個下標從 0 開始的整數陣列 arr 和一個 m x n 的整數 矩陣 mat 。arr 和 mat 都包含範圍 [1，m * n] 內的 所有 整數。

從下標 0 開始遍歷 arr 中的每個下標 i ，並將包含整數 arr[i] 的 mat 單元格塗色。

請你找出 arr 中在 mat 的某一行或某一列上都被塗色且下標最小的元素，並返回其下標 i 。

範例 1：

輸入：arr = [1,3,4,2], mat = [[1,4],[2,3]]
輸出：2
解釋：遍歷如上圖所示，arr[2] 在矩陣中的第一行或第二列上都被塗色。

範例 2：

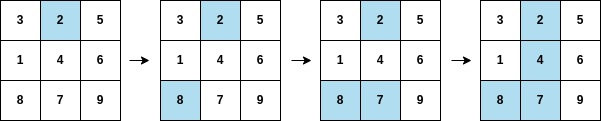
輸入：arr = [2,8,7,4,1,3,5,6,9], mat = [[3,2,5],[1,4,6],[8,7,9]]
輸出：3
解釋：遍歷如上圖所示，arr[3] 在矩陣中的第二列上都被塗色。

提示：

• m == mat.length
• n = mat[i].length
• arr.length == m * n
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 1 <= arr[i], mat[r][c] <= m * n
• arr 中的所有整數 互不相同
• mat 中的所有整數 互不相同

問題結構化

1、概括問題目標

計算塗滿一行或一列時的最小下標。

2、觀察資料特徵

arr 陣列和 mat 矩陣中的所有整數都沒有重複數。

3、分析問題要件

• 塗色：使用 arr 陣列對 mat 矩陣塗色；
• 終止條件：當存在一行或一列被塗滿時，返回當前的 arr 陣列下標。

至此，程式整體框架確定：

for (數位 in arr 陣列) {
    塗色
    if (塗滿一行或一列) 返回索引
}
return -1 // 問題一定有解

4、提高抽象程度

• 查詢：對 mat 矩陣中的相同數位的單元格塗色時，需要查詢數位在矩陣中的位置：
• 計數：結合「無重複數」的資料特徵，判斷是否存在一行或一列被塗滿時，就是判斷一行或一列中被塗色的計數是否達到行數或列數。

5、具體化解決手段

如何查詢數位的位置？

• 手段 1（暴力列舉）：列舉 mat 矩陣，直到匹配目標數位時停止；
• 手段 2（雜湊表）：結合「無重複數」的資料特徵，可以預處理 mat 矩陣獲得數位和位置的對映關係，在塗色時以 O(1) 時間複雜度定位塗色位置。

如何判斷達到終止條件？

• 手段 1（暴力列舉）：列舉 mat 矩陣的行列，當一行或一列的塗色個數達到行數或列數時停止；
• 手段 2（計數陣列）：記錄每一行和每一列的塗色計數，當計數達到行數或列數時，說明達到終止條件。

題解（雜湊表 + 計數）

題目的關鍵資訊是「無重複數」，根據問題分析模擬即可：

class Solution {
    fun firstCompleteIndex(arr: IntArray, mat: Array<IntArray>): Int {
        val n = mat.size
        val m = mat[0].size
        // 計數陣列
        val rows = IntArray(n)
        val columns = IntArray(m)
        // 雜湊表
        val hashMap = HashMap<Int, IntArray>()
        // 預處理
        for (i in 0 until n) {
            for (j in 0 until m) {
                hashMap[mat[i][j]] = intArrayOf(i, j)
            }
        }
        // 塗色
        for ((i, e) in arr.withIndex()) {
            val node = hashMap[e]!!
            // 判斷
            if (++rows[node[0]] == m || ++columns[node[1]] == n) return i
        }
        return -1
    }
}

複雜度分析：

• 時間複雜度：$O(nm)$ 其中 n 和 m 分別為矩陣的行數和列數，預處理和塗色分別對每個元素存取 1 次；
• 空間複雜度：$O(nm)$ 雜湊表和計數陣列空間。

---

Q3. 前往目標的最小代價（Medium）

https://leetcode.cn/problems/minimum-cost-of-a-path-with-special-roads/

題目描述

給你一個陣列 start ，其中 start = [startX, startY] 表示你的初始位置位於二維空間上的 (startX, startY) 。另給你一個陣列 target ，其中 target = [targetX, targetY] 表示你的目標位置 (targetX, targetY) 。

從位置 (x1, y1) 到空間中任一其他位置 (x2, y2) 的代價是 |x2 - x1| + |y2 - y1| 。

給你一個二維陣列 specialRoads ，表示空間中存在的一些特殊路徑。其中 specialRoads[i] = [x1i, y1i, x2i, y2i, costi] 表示第 i 條特殊路徑可以從 (x1i, y1i) 到 (x2i, y2i) ，但成本等於 costi 。你可以使用每條特殊路徑任意次數。

返回從 (startX, startY) 到 (targetX, targetY) 所需的最小代價。

範例 1：

輸入：start = [1,1], target = [4,5], specialRoads = [[1,2,3,3,2],[3,4,4,5,1]]
輸出：5
解釋：從 (1,1) 到 (4,5) 的最優路徑如下：
- (1,1) -> (1,2) ，移動的代價是 |1 - 1| + |2 - 1| = 1 。
- (1,2) -> (3,3) ，移動使用第一條特殊路徑，代價是 2 。
- (3,3) -> (3,4) ，移動的代價是 |3 - 3| + |4 - 3| = 1.
- (3,4) -> (4,5) ，移動使用第二條特殊路徑，代價是 1 。
總代價是 1 + 2 + 1 + 1 = 5 。
可以證明無法以小於 5 的代價完成從 (1,1) 到 (4,5) 。

範例 2：

輸入：start = [3,2], target = [5,7], specialRoads = [[3,2,3,4,4],[3,3,5,5,5],[3,4,5,6,6]]
輸出：7
解釋：最優路徑是不使用任何特殊路徑，直接以 |5 - 3| + |7 - 2| = 7 的代價從初始位置到達目標位置。

提示：

• start.length == target.length == 2
• 1 <= startX <= targetX <= 105
• 1 <= startY <= targetY <= 105
• 1 <= specialRoads.length <= 200
• specialRoads[i].length == 5
• startX <= x1i, x2i <= targetX
• startY <= y1i, y2i <= targetY
• 1 <= costi <= 105

預備知識 · 最短路演演算法

這道題是最短路問題，先回顧下幾種最短路演演算法的區別：

• Floyd 演演算法（多源匯正權最短路）
  • 適用於求任意節點之間的最短路，需要三層迴圈列舉中轉點 i、列舉起點 j 和列舉終點 k，時間複雜度最高。
• Bellman Ford 演演算法（單源負權最短路）
  • 在每一輪迭代中，嘗試對圖上每一條邊進行鬆弛，直到沒有鬆弛操作時結束。
• Dijkstra 演演算法（單源正權最短路）：
  • 在每一輪迭代中，使用確定集中最短路長度最小的節點去鬆弛相鄰節點，由於負權邊會破壞貪心策略的選擇，無法處理負權問題；
  • 稀疏圖小頂堆的寫法更優，稠密圖樸素寫法更優。

最短路演演算法	Floyd	Bellman-Ford	Dijkstra	Johnson
最短路型別	每對結點之間的最短路	單源最短路	單源最短路	每對結點之間的最短路
作用於	任意圖	任意圖	非負權圖	任意圖
能否檢測負環？	能	能	不能	能
時間複雜度	O(n^3)	O(nm)	O(mlgn)最小堆	O(nmlgm)

其中 n 是節點數，m 是邊數。

問題結構化

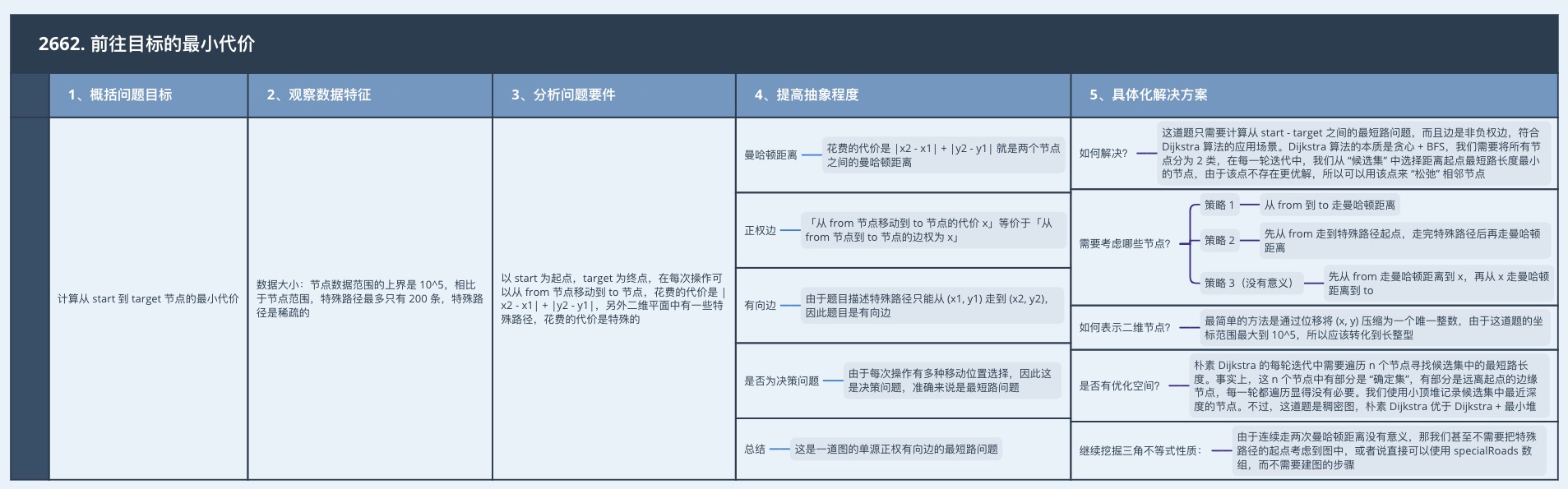
1、概括問題目標

計算從 start 到 target 節點的最小代價。

2、觀察資料特徵

• 資料大小：節點資料範圍的上界是 10^5，相比於節點範圍，特殊路徑最多隻有 200 條，特殊路徑是稀疏的。

3、分析問題要件

以 start 為起點，target 為終點，在每次操作可以從 from 節點移動到 to 節點，花費的代價是 |x2 - x1| + |y2 - y1|，另外二維平面中有一些特殊路徑，花費的代價是特殊的。

4、提高抽象程度

• 曼哈頓距離：花費的代價是 |x2 - x1| + |y2 - y1| 就是兩個節點之間的曼哈頓距離；
• 正權邊：「從 from 節點移動到 to 節點的代價 x」等價於「從 from 節點到 to 節點的邊權為 x」；
• 有向邊：由於題目描述特殊路徑只能從 (x1, y1) 走到 (x2, y2)，因此題目是有向邊；
• 是否為決策問題？由於每次操作有多種移動位置選擇，因此這是決策問題，準確來說是最短路問題；
• 總結：這是一道圖的單源正權有向邊的最短路問題。

5、具體化解決方案

如何解決圖的單源正權最短路問題？

這道題只需要計算從 start - target 之間的最短路問題，而且邊是非負權邊，符合 Dijkstra 演演算法的應用場景。Dijkstra 演演算法的本質是貪心 + BFS，我們需要將所有節點分為 2 類，在每一輪迭代中，我們從 「候選集」 中選擇距離起點最短路長度最小的節點，由於該點不存在更優解，所以可以用該點來 「鬆弛」 相鄰節點。

• 1、確定集：已確定（從起點開始）到當前節點最短路徑的節點；
• 2、候選集：未確定（從起點開始）到當前節點最短路徑的節點。

需要考慮哪些節點？

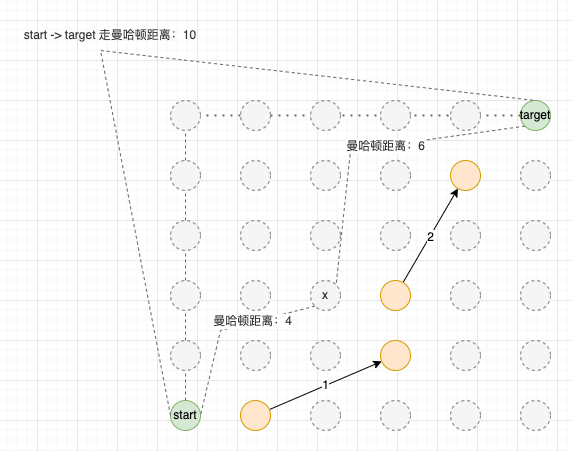
這道題沒有限制只能走特殊路徑，那麼是不是二維平面上所有節點都需要考慮在呢？其實需要，結合「三角不等式」觀察，我們發現兩個點連續走兩次曼哈頓距離沒有意義，也就是說，目標路徑一定是在起點、終點和特殊路徑節點中間移動。

• 策略 1：從 from 到 to 走曼哈頓距離；
• 策略 2：先從 from 走到特殊路徑起點，走完特殊路徑後再走曼哈頓距離；
• 策略 3（沒有意義）：先從 from 走曼哈頓距離到 x，再從 x 走曼哈頓距離到 to。

如何表示二維節點？

最簡單的方法是通過位移將 (x, y) 壓縮為一個唯一整數，由於這道題的座標範圍最大到 10^5，所以應該轉化到長整型。

val U = 100000L // 數值上界 + 1

壓縮：
val key = x * U + y

還原：
val x = (key / U).toInt()
val y = (key % U).toInt()

至此，我們可以使用樸素 Dijkstra 演演算法模擬問題。

是否有優化空間？

樸素 Dijkstra 的每輪迭代中需要遍歷 n 個節點尋找候選集中的最短路長度。事實上，這 n 個節點中有部分是 「確定集」，有部分是遠離起點的邊緣節點，每一輪都遍歷顯得沒有必要。我們使用小頂堆記錄候選集中最近深度的節點。不過，這道題是稠密圖，樸素 Dijkstra 優於 Dijkstra + 最小堆。

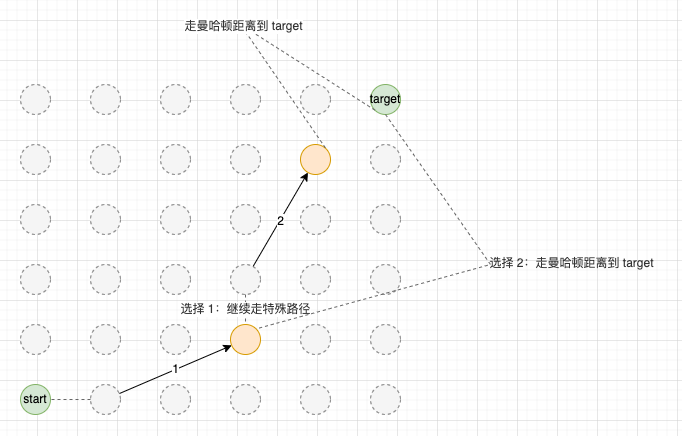
繼續挖掘三角不等式性質：

由於連續走兩次曼哈頓距離沒有意義，那我們甚至不需要把特殊路徑的起點考慮到圖中，或者說直接可以使用 specialRoads 陣列，而不需要建圖的步驟。

6、答疑

• 這道題的資料範圍到 10^5，而特殊路徑最多隻有 200 條，不是應該算稀疏圖？

這個觀點混淆了稠密圖的定義，稠密或稀疏取決於邊數相對於節點數的大小。簡單來說，在節點數固定的情況下，邊數越大則圖越稠密。在這道題中，每個節點都存在到其他所有節點的路徑，因此不僅是稠密圖，甚至是完全圖。

題解一（樸素 Dijkstra）

• 使用 Dijkstra 演演算法解決最短路問題。

class Solution {
    fun minimumCost(start: IntArray, target: IntArray, specialRoads: Array<IntArray>): Int {
        // 單源正權最短路
        val U = 100001L // 數值上界 + 1
        val INF = 0x3F3F3F3F

        val startL = start[0] * U + start[1]
        val targetL = target[0] * U + target[1]

        if (startL == targetL) return 0
        
        // 1、節點與最短路長度
        val nodes = HashMap<Long, Int>()
        // 1.1 特殊路徑上的節點
        for (road in specialRoads) {
            // 過濾無意義的特殊路徑（路徑花費大於曼哈頓距離）
            nodes[road[0] * U + road[1]] = INF
            nodes[road[2] * U + road[3]] = INF
        }
        // 1.2 起點節點與終點節點
        nodes[targetL] = INF
        nodes[startL] = 0 // 起點可能為終點，如果開頭不做特判需要注意順序
        // 2、建有向圖（鄰接表）<from -> <to -> cost>>
        val graph = HashMap<Long, HashMap<Long, Int>>()
        // 2.1 節點之間的路徑（雙向邊）
        for ((from, _) in nodes) {
            graph[from] = HashMap<Long, Int>()
            val fromX = (from / U).toInt()
            val fromY = (from % U).toInt()
            for ((to, _) in nodes) {
                if (from == to) continue
                val toX = (to / U).toInt()
                val toY = (to % U).toInt()
                graph[from]!![to] = Math.abs(toX - fromX) + Math.abs(toY - fromY)
            }
        }
        // 2.2 特殊路徑（單向邊）
        for (road in specialRoads) {
            val from = road[0] * U + road[1]
            val to = road[2] * U + road[3]
            graph[from]!![to] = Math.min(graph[from]!!.getOrDefault(to, INF), road[4]) // 特殊路徑的花費可能更長
        }
        // 3、存取標記
        val visit = HashSet<Long>()
        // 4、樸素 Dijkstra
        while (true) {
            // 尋找候選集中最短路長度最短的節點
            var minNode = -1L
            var minDis = -1
            for ((to, dis) in nodes) {
                if (visit.contains(to)) continue
                if (minDis == -1 || dis < minDis) {
                    minDis = dis
                    minNode = to
                }
            }
            // println("minNode=$minNode, minDis=$minDis")
            // 找到目標點的最短路長度
            if (minNode == targetL) return minDis
            // 存取標記
            visit.add(minNode)
            // 鬆弛相鄰節點
            for ((to, cost) in graph[minNode]!!) {
                // println("to=$to, cost=$cost")
                if (minDis + cost < nodes[to]!!) {
                    nodes[to] = minDis + cost
                }
            }
        }
        return -1 // 必然有解
    }
}

複雜度分析：

• 時間複雜度：$O(n^2)$ 其中 n 是 specialRoads 特殊路徑陣列的長度；
• 空間複雜度：$O(n^2)$ 圖空間 + 標記陣列空間。

題解二（Dijkstra 優化）

• 優化：剪去圖空間。

class Solution {
    fun minimumCost(start: IntArray, target: IntArray, specialRoads: Array<IntArray>): Int {
        // 單源正權最短路
        val U = 100001L // 數值上界 + 1
        val INF = 0x3F3F3F3F

        val startL = start[0] * U + start[1]
        val targetL = target[0] * U + target[1]

        if (startL == targetL) return 0

        // 1、節點與最短路長度
        val nodes = HashMap<Long, Int>()
        // 起點節點與終點節點
        nodes[targetL] = INF
        nodes[startL] = 0 // 起點可能為終點，如果開頭不做特判需要注意順序
        // 2、存取標記
        val visit = HashSet<Long>()
        // 3、樸素 Dijkstra
        while (true) {
            // 尋找候選集中最短路長度最短的節點
            var minNode = -1L
            var minDis = -1
            for ((to, dis) in nodes) {
                if (visit.contains(to)) continue
                if (minDis == -1 || dis < minDis) {
                    minDis = dis
                    minNode = to
                }
            }
            // println("minNode=$minNode, minDis=$minDis")
            // 找到目標點的最短路長度
            if (minNode == targetL) return minDis
            // 存取標記
            visit.add(minNode)
            val minNodeX = (minNode / U).toInt()
            val minNodeY = (minNode % U).toInt()
            // 1、直接到終點
            nodes[targetL] = Math.min(nodes[targetL]!!, minDis + Math.min(nodes[targetL]!!, (target[1] - minNodeY) + (target[0] - minNodeX)))
            // 2、先經過特殊路徑（minNode -> 特殊路徑的起點 -> 特殊路徑的終點）
            for (road in specialRoads) {
                val specialTo = road[2] * U + road[3]
                if (specialTo == minNode) continue // 重複路徑
                val specialDis = minDis + Math.abs(road[0] - minNodeX) + Math.abs(road[1] - minNodeY) + road[4]
                if (specialDis < nodes.getOrDefault(specialTo, INF)) {
                    nodes[specialTo] = specialDis
                }
            }
        }
        return -1 // 必然有解
    }
}

複雜度分析：

• 時間複雜度：$O(n^2)$ 其中 n 是 specialRoads 特殊路徑陣列的長度；
• 空間複雜度：$O(n)$ 標記陣列空間。

題解三（Dijkstra + 最小堆）

附贈一份 Dijkstra + 最小堆的程式碼：

class Solution {
    fun minimumCost(start: IntArray, target: IntArray, specialRoads: Array<IntArray>): Int {
        // 單源正權最短路
        val U = 100000L // 數值上界 + 1
        val INF = 0x3F3F3F3F

        val startL = start[0] * U + start[1]
        val targetL = target[0] * U + target[1]

        if (startL == targetL) return 0

        // 1、節點與最短路長度
        val nodes = HashMap<Long, Int>()
        // 起點節點與終點節點
        nodes[targetL] = INF
        nodes[startL] = 0 // 起點可能為終點，如果開頭不做特判需要注意順序
        // 2、最小堆
        val heap = PriorityQueue<Long>() { l1, l2 ->
            nodes.getOrDefault(l1, INF) - nodes.getOrDefault(l2, INF)
        }
        heap.offer(startL)
        heap.offer(targetL)
        // 3、Dijkstra
        while (!heap.isEmpty()) {
            // 候選集中最短路長度最短的節點
            val minNode = heap.poll()
            val minDis = nodes[minNode]!!
            // println("minNode=$minNode, minDis=$minDis")
            // 找到目標點的最短路長度
            if (minNode == targetL) return minDis
            val minNodeX = (minNode / U).toInt()
            val minNodeY = (minNode % U).toInt()
            // 1、直接到終點
            val newDirectToTarget = minDis + Math.min(nodes[targetL]!!, (target[1] - minNodeY) + (target[0] - minNodeX))
            if (newDirectToTarget < nodes[targetL]!!) {
                nodes[targetL] = newDirectToTarget
                heap.offer(targetL)
            }
            // 2、先經過特殊路徑（minNode -> 特殊路徑的起點 -> 特殊路徑的終點）
            for (road in specialRoads) {
                val specialTo = road[2] * U + road[3]
                if (specialTo == minNode) continue // 重複路徑
                val specialDis = minDis + Math.abs(road[0] - minNodeX) + Math.abs(road[1] - minNodeY) + road[4]
                if (specialDis < nodes.getOrDefault(specialTo, INF)) {
                    nodes[specialTo] = specialDis
                    heap.offer(specialTo)
                }
            }
        }
        return -1 // 必然有解
    }
}

複雜度分析：

• 時間複雜度：$O(m·lgn)$ 其中 n 是 specialRoads 特殊路徑陣列的長度，m 是邊數，由於這道題是完全圖，所以有 m = n^2；
• 空間複雜度：$O(n)$ 標記陣列空間。

近期周賽最短路問題：

• 2612. 最少翻轉運算元（Hard）
• 2608. 圖中的最短環（Hard）
• 2577. 在網格圖中存取一個格子的最少時間（Hard）

---

Q4. 字典序最小的美麗字串（Hard）

https://leetcode.cn/problems/lexicographically-smallest-beautiful-string/

題目描述

如果一個字串滿足以下條件，則稱其為 美麗字串 ：

• 它由英語小寫字母表的前 k 個字母組成。
• 它不包含任何長度為 2 或更長的迴文子字串。

給你一個長度為 n 的美麗字串 s 和一個正整數 k 。

請你找出並返回一個長度為 n 的美麗字串，該字串還滿足：在字典序大於 s 的所有美麗字串中字典序最小。如果不存在這樣的字串，則返回一個空字串。

對於長度相同的兩個字串 a 和 b ，如果字串 a 在與字串 b 不同的第一個位置上的字元字典序更大，則字串 a 的字典序大於字串 b 。

• 例如，"abcd" 的字典序比 "abcc" 更大，因為在不同的第一個位置（第四個字元）上 d 的字典序大於 c 。

範例 1：

輸入：s = "abcz", k = 26
輸出："abda"
解釋：字串 "abda" 既是美麗字串，又滿足字典序大於 "abcz" 。
可以證明不存在字串同時滿足字典序大於 "abcz"、美麗字串、字典序小於 "abda" 這三個條件。

範例 2：

輸入：s = "dc", k = 4
輸出：""
解釋：可以證明，不存在既是美麗字串，又字典序大於 "dc" 的字串。

提示：

• 1 <= n == s.length <= 105
• 4 <= k <= 26
• s 是一個美麗字串

問題結構化

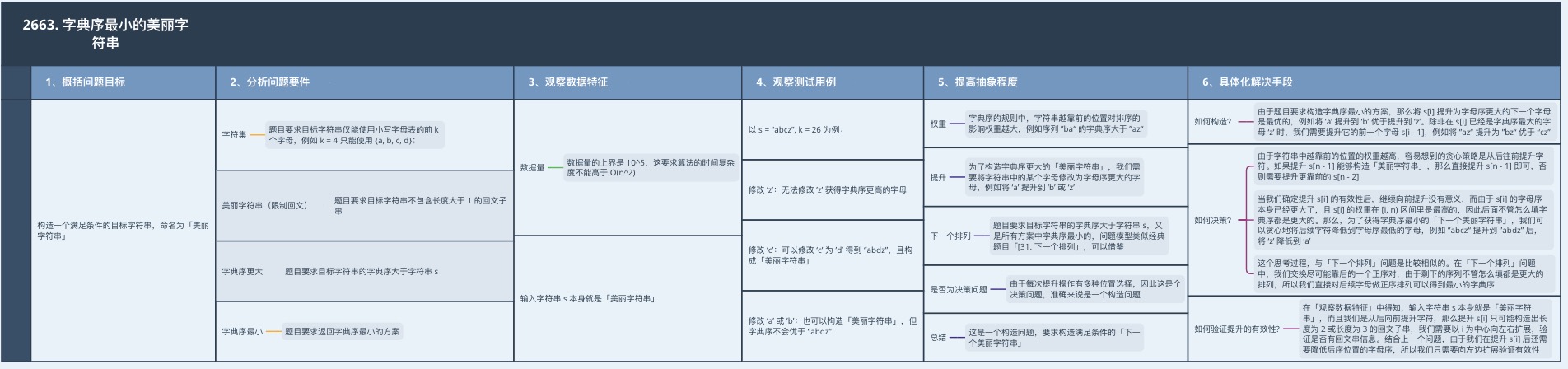
1、概括問題目標

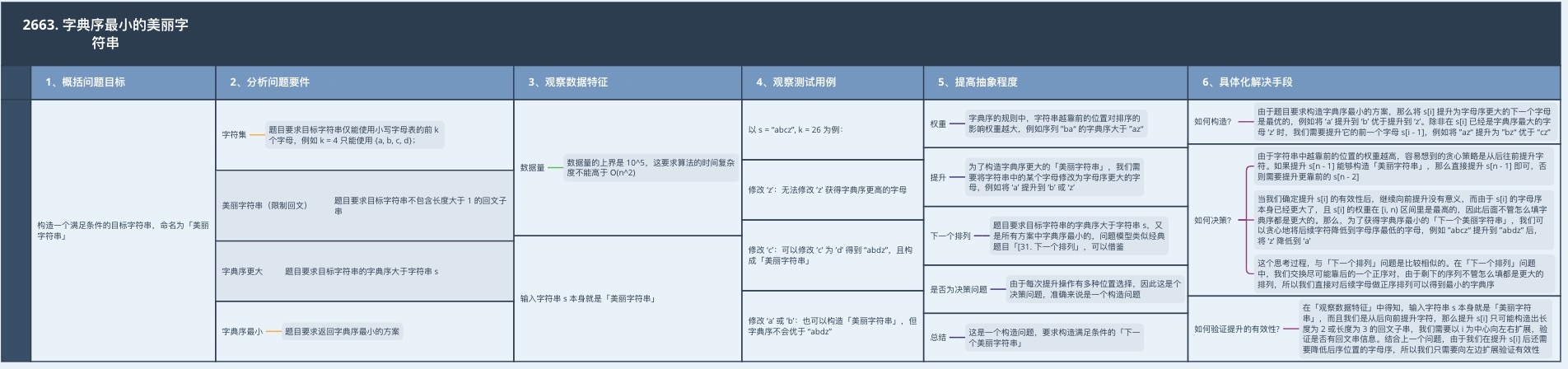
構造一個滿足條件的目標字串，命名為「美麗字串」。

2、分析問題要件

• 字元集：題目要求目標字串僅能使用小寫字母表的前 k 個字母，例如 k = 4 只能使用 {a, b, c, d}；
• 美麗字串（限制迴文）：題目要求目標字串不包含長度大於 1 的迴文子串；
• 字典序更大：題目要求目標字串的字典序大於字串 s；
• 字典序最小：題目要求返回字典序最小的方案；

3、觀察資料特徵

• 資料量：資料量的上界是 10^5，這要求演演算法的時間複雜度不能高於 O(n^2)；
• 輸入字串 s 本身就是「美麗字串」。

4、觀察測試用例

以 s = 「abcz」, k = 26 為例：

• 修改 ‘z’：無法修改 ’z’ 獲得字典序更高的字母；
• 修改 ‘c’：可以修改 ‘c’ 為 ’d’ 得到 「abdz」，且構成「美麗字串」；
• 修改 ‘a’ 或 ’b’：也可以構造「美麗字串」，但字典序不會優於 「abdz」。

5、提高抽象程度

• 權重：字典序的規則中，字串越靠前的位置對排序的影響權重越大，例如序列 」ba「 的字典序大於 」az「；
• 提升：為了構造字典序更大的「美麗字串」，我們需要將字串中的某個字母修改為字母序更大的字母，例如將 ‘a’ 提升到 ‘b’ 或 ‘z’；
• 下一個排列：題目要求目標字串的字典序大於字串 s，又是所有方案中字典序最小的，問題模型類似經典題目「31. 下一個排列」，可以借鑑；
• 是否為決策問題：由於每次提升操作有多種位置選擇，因此這是個決策問題，準確來說是一個構造問題。
• 總結：這是一個構造問題，要求構造滿足條件的「下一個美麗字串」。

6、具體化解決手段

如何構造滿足條件的「下一個美麗字串」？

由於題目要求構造字典序最小的方案，那麼將 s[i] 提升為字母序更大的下一個字母是最優的，例如將 ’a’ 提升到 ‘b’ 優於提升到 ‘z’。除非在 s[i] 已經是字典序最大的字母 ‘z’ 時，我們需要提升它的前一個字母 s[i - 1]，例如將 」az「 提升為 」bz「 優於 「cz」。

構造「下一個美麗字串」需要提升字母序，那麼如何決策替換策略？

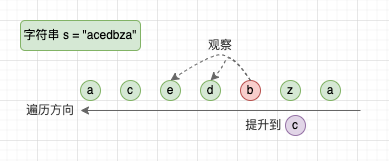
由於字串中越靠前的位置的權重越高，容易想到的貪心策略是從後往前提升字元。如果提升 s[n - 1] 能夠構造「美麗字串」，那麼直接提升 s[n - 1] 即可，否則需要提升更靠前的 s[n - 2]。

當我們確定提升 s[i] 的有效性後，繼續向前提升沒有意義，而由於 s[i] 的字母序本身已經更大了，且 s[i] 的權重在 [i, n) 區間裡是最高的，因此後面不管怎麼填字典序都是更大的。那麼，為了獲得字典序最小的「下一個美麗字串」，我們可以貪心地將後續字元降低到字母序最低的字母，例如 」abcz「 提升到 」abdz」 後，將 ‘z’ 降低到 ‘a’。

這個思考過程，與「下一個排列」問題是比較相似的。在「下一個排列」問題中，我們交換儘可能靠後的一個正序對，由於剩下的序列不管怎麼填都是更大的排列，所以我們直接對後續字母做正序排列可以得到最小的字典序。

如何驗證提升的有效性（提升字母序後會可能引入新的迴文資訊）？

在「觀察資料特徵」中得知，輸入字串 s 本身就是「美麗字串」，而且我們是從後向前提升字元，那麼提升 s[i] 只可能構造出長度為 2 或長度為 3 的迴文子串，我們需要以 i 為中心向左右擴充套件，驗證是否有迴文串資訊。結合上一個問題，由於我們在提升 s[i] 後還需要降低後序位置的字母序，所以我們只需要向左邊擴充套件驗證有效性。

至此，我們可以確定整體框架，分為 2 個階段：

階段一：

提升 s[n - 1]
while (i 從後往前遍歷) {
		for (c in s[i] + 1 until 'a' + k) { // 列舉字元集
				if (存在迴文資訊) continue
				s[i] = c // 確定有效性
				// 記錄下標 i
		}
		// 無法提升 s[i]，嘗試提升 s[i - 1]
}

階段二：

// 將 [i + 1, n) 降低為最小字元
for(j in i + 1 until n) {
		for (c in 'a' until 'a' + k) { // 列舉字元集
				if (存在迴文資訊）continue
				s[j] = c
				break
		}
}

答疑：

• 為什麼階段二沒有處理無法構造的情況？

由於題目提示 k 的取值範圍是大於等於 4 的，也就是字元集的大小最小為 4，而驗證「有效性」只需要觀察位置 i 的前兩個位置。那麼在長度為 3 的子區間 [i-2, i] 中，我們總能夠從大小為 4 的字元集中，選擇出一個不會構造出迴文資訊的子串。因此，階段二是必然可構造的。甚至來說，題目將 k 的取值範圍修改到 [3, 26]，我們的演演算法也是成立的。

題解（貪心）

class Solution {
    fun smallestBeautifulString(s: String, k: Int): String {
        val n = s.length
        val U = 'a' + k
        val sArray = s.toCharArray()
        var pos = -1
        outer@ for (i in n - 1 downTo 0) {
            // 嘗試提升字母序
            for (c in sArray[i] + 1 until U) {
                // 驗證有效性（只需要驗證左邊）
                if ((i > 0 && c == sArray[i - 1]) || (i > 1 && c == sArray[i - 2])) continue
                sArray[i] = c
                pos = i
                break@outer
            }
        }

        // 無法構造
        if (pos < 0) return ""

        for (i in pos + 1 until n) {
            for (c in 'a' until U) {
                // 驗證有效性（只需要驗證左邊）
                if ((i > 0 && c == sArray[i - 1]) || (i > 1 && c == sArray[i - 2])) continue
                sArray[i] = c
                break
            }
        }

        return String(sArray)
    }
}

複雜度分析：

• 時間複雜度：$O(n)$ 其中 n 為字串 s 的長度，每個位置最多被存取 2 次，而每個位置的提升操作最多執行 2 次，降低操作最多執行 2 次；
• 空間複雜度：$O(1)$ 不考慮結果陣列。

相似問題：

• 31. 下一個排列
• 647. 迴文子串