「學習筆記」可持久化線段樹
可持久化資料結構 (Persistent data structure) 總是可以保留每一個歷史版本,並且支援操作的不可變特性 (immutable)。
主席樹全稱是可持久化權值線段樹,給定 \(n\) 個整數構成的序列 \(a\),將對於指定的閉區間 \(\left[l, r\right]\) 查詢其區間內的第 \(k\) 小值。
可持久化線段樹
變數
#define mid ((l + r) >> 1)
int rot;
int rt[M];
struct node {
int l, r, val;
} nod[M];
l, r: 左右孩子的指標;
val: 權值;
rot: 動態開點計數器;
rt: 不同版本的根節點的編號。
過程
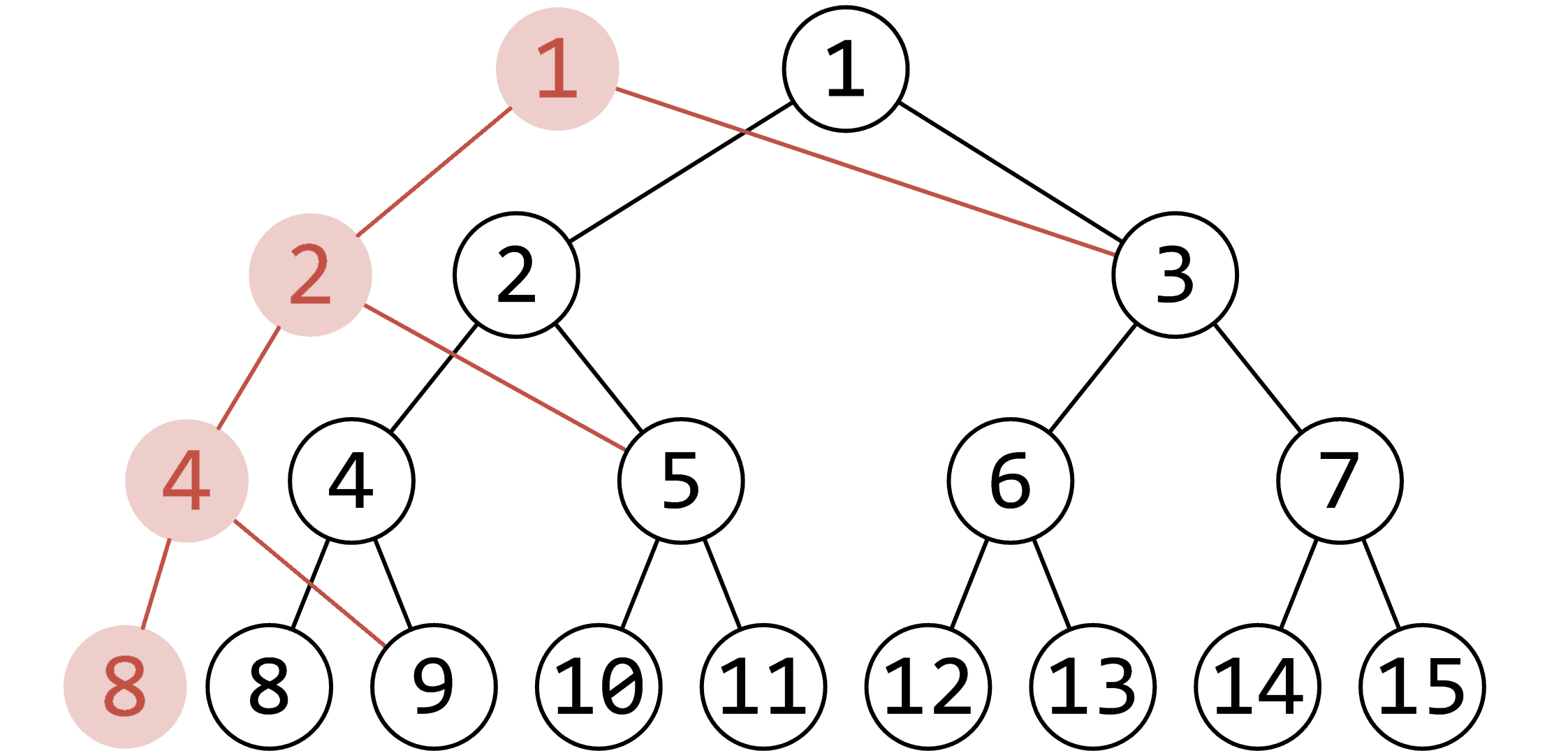
每次修改操作修改的點的個數是一樣的。
(例如上圖,修改了 \(\left[1,8\right]\) 中對應權值為 \(1\) 的結點,紅色的點即為更改的點)
只更改了 \(O_{\log{n}}\) 個結點,形成一條鏈,也就是說每次更改的結點數 \(=\) 樹的高度。
主席樹不能使用 \(x\times 2,x\times 2+1\) 來表示左右兒子,而是應該動態開點,並儲存每個節點的左右兒子編號。
在記錄左右兒子的基礎上,儲存插入每個數的時候的根節點就可以實現持久化。
現在還有個問題,如何求 \(\left[l,r\right]\) 區間 \(k\) 小值。
這裡我們再聯絡另外一個知識:字首和。
這個小東西巧妙運用了區間減法的性質,通過預處理從而達到 \(O_1\) 回答每個詢問。
我們可以發現,主席樹統計的資訊也滿足這個性質。
如果需要得到 \(\left[l,r\right]\) 的統計資訊,只需要用 \(\left[1,r\right]\) 的資訊減去 \(\left[1,l - 1\right]\) 的資訊就行了。
關於空間問題,直接上個 \(2^5\times 10^5\)(即 n << 5,大多數題目中空間限制都較為寬鬆,因此一般不用擔心空間超限的問題)。
操作
-
建樹
int build(int l, int r) {
int u = ++ rot;
if (l == r) {
return u;
}
nod[u].l = build(l, mid);
nod[u].r = build(mid + 1, r);
return u;
}
-
建立新節點
inline int newnod(int u) {
++ rot;
nod[rot] = nod[u];
nod[rot].val = nod[u].val + 1;
return rot;
}
修改時是在原來版本的基礎上進行修改,先設定它們一樣,由於插入了一個新的數,所以 nod[rot].val = nod[u].val + 1;。
-
插入新節點
int add(int u, int l, int r, int pos) {
u = newnod(u);
if (l == r) return u;
if (pos <= mid) {
nod[u].l = add(nod[u].l, l, mid, pos);
}
else {
nod[u].r = add(nod[u].r, mid + 1, r, pos);
}
return u;
}
if (pos <= mid) {
nod[u].l = add(nod[u].l, l, mid, pos);
}
else {
nod[u].r = add(nod[u].r, mid + 1, r, pos);
}
修改時只會修改一條鏈,那也就意味著只會修改左孩子或右孩子中的一個,另一個保持不變。
-
查詢第 \(k\) 大
int query(int l, int r, int lr, int rr, int k) {
int x = nod[nod[rr].l].val - nod[nod[lr].l].val;
if (l == r) return l;
if (k <= x) {
return query(l, mid, nod[lr].l, nod[rr].l, k);
}
else {
return query(mid + 1, r, nod[lr].r, nod[rr].r, k - x);
}
}
int x = nod[nod[rr].l].val - nod[nod[lr].l].val;
這裡利用了字首和,求的是在 \(lr\) 到 \(rr\) 這個版本之間,左孩子的數量增加了多少,即 \(\left[lr, rr\right]\) 的前 \(x\) 小的元素。
if (k <= x) {
return query(l, mid, nod[lr].l, nod[rr].l, k);
}
else {
return query(mid + 1, r, nod[lr].r, nod[rr].r, k - x);
}
如果 \(k < x\),那麼說明第 \(k\) 大的數在右孩子上,否則就在左子樹上。
可持久化陣列
這個來源於洛谷的【模板】可持久化線段樹 1(可持久化陣列),需要支援修改操作,但沒有了查詢第 \(k\) 大操作和插入操作。
變數
#define mid ((l + r) >> 1)
int rot;
int rt[M];
struct node {
int ls, rs, val;
} nod[(N << 5) + 10];
操作
-
建立新節點
inline int newnod(int u) { // 建立新節點
++ rot;
nod[rot] = nod[u];
return rot;
}
-
建樹
int build(int l, int r) { // 建樹
int u = ++ rot;
if (l == r) {
scanf("%d", &nod[u].val);
return u;
}
nod[u].ls = build(l, mid);
nod[u].rs = build(mid + 1, r);
return u;
}
-
修改
int modify(int u, int l, int r, int pos, int c) { // 修改
u = newnod(u);
if (l == r) {
nod[u].val = c;
}
else {
if (pos <= mid) {
nod[u].ls = modify(nod[u].ls, l, mid, pos, c);
}
else {
nod[u].rs = modify(nod[u].rs, mid + 1, r, pos, c);
}
}
return u;
}
-
查詢
int query(int u, int l, int r, int pos) { // 查詢
if (l == r) {
return nod[u].val;
}
else {
if (pos <= mid) {
return query(nod[u].ls, l, mid, pos);
}
else {
return query(nod[u].rs, mid + 1, r, pos);
}
}
}
模板
namespace Persistent { // 可持久化資料結構
#define mid ((l + r) >> 1)
const int N = 1e6 + 5;
const int M = (N << 5) + 10;
struct persistent_arr { // 可持久化陣列
int rot;
int rt[M];
struct node {
int ls, rs, val;
} nod[(N << 5) + 10];
inline int newnod(int u) { // 建立新節點
++ rot;
nod[rot] = nod[u];
return rot;
}
int build(int l, int r) { // 建樹
int u = ++ rot;
if (l == r) {
scanf("%d", &nod[u].val);
return u;
}
nod[u].ls = build(l, mid);
nod[u].rs = build(mid + 1, r);
return u;
}
int modify(int u, int l, int r, int pos, int c) { // 修改
u = newnod(u);
if (l == r) {
nod[u].val = c;
}
else {
if (pos <= mid) {
nod[u].ls = modify(nod[u].ls, l, mid, pos, c);
}
else {
nod[u].rs = modify(nod[u].rs, mid + 1, r, pos, c);
}
}
return u;
}
int query(int u, int l, int r, int pos) { // 查詢
if (l == r) {
return nod[u].val;
}
else {
if (pos <= mid) {
return query(nod[u].ls, l, mid, pos);
}
else {
return query(nod[u].rs, mid + 1, r, pos);
}
}
}
};
struct persistent_seg {
int rot;
int rt[M];
struct node {
int l, r, val;
} nod[M];
inline int newnod(int u) { // 建立新節點
++ rot;
nod[rot] = nod[u];
nod[rot].val = nod[u].val + 1;
return rot;
}
int build(int l, int r) { // 建樹
int u = ++ rot;
if (l == r) {
return u;
}
nod[u].l = build(l, mid);
nod[u].r = build(mid + 1, r);
return u;
}
int add(int u, int l, int r, int pos) { // 插入新節點
u = newnod(u);
if (l == r) return u;
if (pos <= mid) {
nod[u].l = add(nod[u].l, l, mid, pos);
}
else {
nod[u].r = add(nod[u].r, mid + 1, r, pos);
}
return u;
}
int query(int l, int r, int lr, int rr, int k) { // 查詢第 k 大的值
int x = nod[nod[rr].l].val - nod[nod[lr].l].val;
if (l == r) return l;
if (k <= x) {
return query(l, mid, nod[lr].l, nod[rr].l, k);
}
else {
return query(mid + 1, r, nod[lr].r, nod[rr].r, k - x);
}
}
};
}
例題
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define mid ((l + r) >> 1)
const int N = 1e6 + 5;
int n, m, rot;
int a[N], rt[N];
inline int read() {
int x = 0;
int fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
struct node {
int ls, rs, val;
} nod[(N << 5) + 10];
inline int newnod(int u) {
++ rot;
nod[rot] = nod[u];
return rot;
}
int build(int l, int r) {
int u = ++ rot;
if (l == r) {
nod[u].val = a[l];
return u;
}
nod[u].ls = build(l, mid);
nod[u].rs = build(mid + 1, r);
return u;
}
int modify(int u, int l, int r, int pos, int c) {
u = newnod(u);
if (l == r) {
nod[u].val = c;
}
else {
if (pos <= mid) {
nod[u].ls = modify(nod[u].ls, l, mid, pos, c);
}
else {
nod[u].rs = modify(nod[u].rs, mid + 1, r, pos, c);
}
}
return u;
}
int query(int u, int l, int r, int pos) {
if (l == r) {
return nod[u].val;
}
else {
if (pos <= mid) {
return query(nod[u].ls, l, mid, pos);
}
else {
return query(nod[u].rs, mid + 1, r, pos);
}
}
}
int main() {
n = read(), m = read();
for (int i = 1; i <= n; ++ i) {
a[i] = read();
}
rt[0] = build(1, n);
for (int i = 1, x, op, pos, val; i <= m; ++ i) {
x = read(), op = read(), pos = read();
if (op == 1) {
val = read();
rt[i] = modify(rt[x], 1, n, pos, val);
}
else {
printf("%d\n", query(rt[x], 1, n, pos));
rt[i] = rt[x];
}
}
}
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define mid ((l + r) >> 1)
const int N = 1e6 + 5;
const int M = (N << 5) + 10;
int n, m;
int rot;
int a[N], tmp[N], rt[N];
struct node {
int l, r, val;
} nod[M];
inline int getid(int c, int len) {
return lower_bound(tmp + 1, tmp + len + 1, c) - tmp;
}
inline int newnod(int u) {
++ rot;
nod[rot] = nod[u];
nod[rot].val = nod[u].val + 1;
return rot;
}
int build(int l, int r) {
int u = ++ rot;
if (l == r) {
return u;
}
nod[u].l = build(l, mid);
nod[u].r = build(mid + 1, r);
return u;
}
int add(int u, int l, int r, int pos) {
u = newnod(u);
if (l == r) return u;
if (pos <= mid) {
nod[u].l = add(nod[u].l, l, mid, pos);
}
else {
nod[u].r = add(nod[u].r, mid + 1, r, pos);
}
return u;
}
int query(int l, int r, int lr, int rr, int k) {
int x = nod[nod[rr].l].val - nod[nod[lr].l].val;
if (l == r) return l;
if (k <= x) {
return query(l, mid, nod[lr].l, nod[rr].l, k);
}
else {
return query(mid + 1, r, nod[lr].r, nod[rr].r, k - x);
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++ i) {
scanf("%d", a + i);
tmp[i] = a[i];
}
sort(tmp + 1, tmp + n + 1);
int len = unique(tmp + 1, tmp + n + 1) - tmp - 1;
rt[0] = build(1, len);
for (int i = 1; i <= n; ++ i) {
rt[i] = add(rt[i - 1], 1, len, getid(a[i], len));
}
for (int i = 1, l, r, k; i <= m; ++ i) {
scanf("%d%d%d", &l, &r, &k);
printf("%d\n", tmp[query(1, len, rt[l - 1], rt[r], k)]);
}
return 0;
}