LeetCode 雙週賽 103（2023/04/29）區間求和的樹狀陣列經典應用

本文已收錄到 AndroidFamily，技術和職場問題，請關注公眾號 [彭旭銳] 提問。

大家好，我是小彭。

這場周賽是 LeetCode 雙週賽第 103 場，難得在五一假期第一天打周賽的人數也沒有少太多。這場比賽前 3 題比較簡單，我們把篇幅留給最後一題。

往期周賽回顧：LeetCode 單週賽第 342 場 · 容斥原理、計數排序、滑動視窗、子陣列 GCB

周賽概覽

Q1. K 個元素的最大和（Easy）

簡單模擬題，不過多講解。

Q2. 找到兩個陣列的字首公共陣列（Medium）

簡單模擬題，在計數的實現上有三種解法：

解法 1：雜湊表 $O(n)$ 空間複雜度
解法 2：技數陣列 $O(n)$ 空間複雜度
解法 3：狀態壓縮 $O(1)$ 空間複雜度

Q3. 網格圖中魚的最大數目（Hard）

這道題的難度標籤是認真的嗎？打 Medium 都過分了居然打 Hard？

解法 1：BFS / DFS $O(nm)$
解法 2：並查集 $O(nm)$

Q4. 將陣列清空（Hard）

這道題的難點在於如何想到以及正確地將原問題轉換為區間求和問題，思路想清楚後用樹狀陣列實現。

解法 1：樹狀陣列 + 索引陣列 $O(nlgn)$
解法 2：樹狀陣列 + 最小堆 $O(nlgn)$

Q1. K 個元素的最大和（Easy）

https://leetcode.cn/problems/maximum-sum-with-exactly-k-elements/

題目描述

給你一個下標從 0 開始的整數陣列 nums 和一個整數 k 。你需要執行以下操作恰好 k 次，最大化你的得分：

從 nums 中選擇一個元素 m 。
將選中的元素 m 從陣列中刪除。
將新元素 m + 1 新增到陣列中。
你的得分增加 m 。

請你返回執行以上操作恰好 k 次後的最大得分。

範例 1：

輸入：nums = [1,2,3,4,5], k = 3
輸出：18
解釋：我們需要從 nums 中恰好選擇 3 個元素並最大化得分。
第一次選擇 5 。和為 5 ，nums = [1,2,3,4,6] 。
第二次選擇 6 。和為 6 ，nums = [1,2,3,4,7] 。
第三次選擇 7 。和為 5 + 6 + 7 = 18 ，nums = [1,2,3,4,8] 。
所以我們返回 18 。
18 是可以得到的最大答案。

範例 2：

輸入：nums = [5,5,5], k = 2
輸出：11
解釋：我們需要從 nums 中恰好選擇 2 個元素並最大化得分。
第一次選擇 5 。和為 5 ，nums = [5,5,6] 。
第二次選擇 6 。和為 6 ，nums = [5,5,7] 。
所以我們返回 11 。
11 是可以得到的最大答案。

提示：

1 <= nums.length <= 100
1 <= nums[i] <= 100
1 <= k <= 100

預備知識 - 等差數列求和

等差數列求和公式：(首項 + 尾項) * 項數 / 2

題解（模擬 + 貪心）

顯然第一次操作的分數會選擇陣列中的最大值 max，後續操作是以 max 為首項的等差數列，直接使用等差數列求和公式即可。

class Solution {
    fun maximizeSum(nums: IntArray, k: Int): Int {
        val max = Arrays.stream(nums).max().getAsInt()
        return (max + max + k - 1) * k / 2
    }
}

複雜度分析：

時間複雜度：$O(n)$ 其中 n 是 nums 陣列的長度；
空間複雜度：$O(1)$

Q2. 找到兩個陣列的字首公共陣列（Medium）

https://leetcode.cn/problems/find-the-prefix-common-array-of-two-arrays/

題目描述

給你兩個下標從 0 開始長度為 n 的整數排列 A 和 B 。

A 和 B 的 字首公共陣列 定義為陣列 C ，其中 C[i] 是陣列 A 和 B 到下標為 i 之前公共元素的數目。

請你返回 A 和 B 的 字首公共陣列 。

如果一個長度為 n 的陣列包含 1 到 n 的元素恰好一次，我們稱這個陣列是一個長度為 n 的排列。

範例 1：

輸入：A = [1,3,2,4], B = [3,1,2,4]
輸出：[0,2,3,4]
解釋：i = 0：沒有公共元素，所以 C[0] = 0 。
i = 1：1 和 3 是兩個陣列的字首公共元素，所以 C[1] = 2 。
i = 2：1，2 和 3 是兩個陣列的字首公共元素，所以 C[2] = 3 。
i = 3：1，2，3 和 4 是兩個陣列的字首公共元素，所以 C[3] = 4 。

範例 2：

輸入：A = [2,3,1], B = [3,1,2]
輸出：[0,1,3]
解釋：i = 0：沒有公共元素，所以 C[0] = 0 。
i = 1：只有 3 是公共元素，所以 C[1] = 1 。
i = 2：1，2 和 3 是兩個陣列的字首公共元素，所以 C[2] = 3 。

提示：

1 <= A.length == B.length == n <= 50
1 <= A[i], B[i] <= n
題目保證 A 和 B 兩個陣列都是 n 個元素的排列。

題解一（雜湊表）

從左到右遍歷陣列，並使用雜湊表記錄存取過的元素，以及兩個陣列交集：

class Solution {
    fun findThePrefixCommonArray(A: IntArray, B: IntArray): IntArray {
        val n = A.size
        val ret = IntArray(n)
        val setA = HashSet<Int>()
        val setB = HashSet<Int>()
        val interSet = HashSet<Int>()
        for (i in 0 until n) {
            setA.add(A[i])
            setB.add(B[i])
            if (setB.contains(A[i])) interSet.add(A[i])
            if (setA.contains(B[i])) interSet.add(B[i])
            ret[i] = interSet.size
        }
        return ret
    }
}

複雜度分析：

時間複雜度：$O(n)$ 其中 n 是 nums 陣列的長度；
空間複雜度：$O(n)$ 雜湊表空間。

題解二（計數陣列）

題解一需要使用多倍空間，我們發現 A 和 B 都是 n 的排列，當存取到的元素 nums[i] 出現 2 次時就必然處於陣列交集中。因此，我們不需要使用雜湊表記錄存取過的元素，而只需要記錄每個元素出現的次數。

class Solution {
    fun findThePrefixCommonArray(A: IntArray, B: IntArray): IntArray {
        val n = A.size
        val ret = IntArray(n)
        val cnt = IntArray(n + 1)
        var size = 0
        for (i in 0 until n) {
            if (++cnt[A[i]] == 2) size ++
            if (++cnt[B[i]] == 2) size ++
            ret[i] = size
        }
        return ret
    }
}

複雜度分析：

時間複雜度：$O(n)$ 其中 n 是 nums 陣列的長度；
空間複雜度：$O(n)$ 計數陣列空間；

題解三（狀態壓縮）

既然 A 和 B 的元素值不超過 50，我們可以使用兩個 Long 變數代替雜湊表優化空間複雜度。

class Solution {
    fun findThePrefixCommonArray(A: IntArray, B: IntArray): IntArray {
        val n = A.size
        val ret = IntArray(n)
        var flagA = 0L
        var flagB = 0L
        var size = 0
        for (i in 0 until n) {
            flagA = flagA or (1L shl A[i])
            flagB = flagB or (1L shl B[i])
            // Kotlin 1.5 才有 Long.countOneBits()
            // ret[i] = (flagA and flagB).countOneBits()
            ret[i] = java.lang.Long.bitCount(flagA and flagB)
        }
        return ret
    }
}

複雜度分析：

時間複雜度：$O(n)$ 其中 n 是 nums 陣列的長度；
空間複雜度：$O(1)$ 僅使用常數級別空間；

Q3. 網格圖中魚的最大數目（Hard）

https://leetcode.cn/problems/maximum-number-of-fish-in-a-grid/description/

題目描述

給你一個下標從 0 開始大小為 m x n 的二維整數陣列 grid ，其中下標在 (r, c) 處的整數表示：

如果 grid[r][c] = 0 ，那麼它是一塊陸地。
如果 grid[r][c] > 0 ，那麼它是一塊水域，且包含 grid[r][c] 條魚。

一位漁夫可以從任意水域格子 (r, c) 出發，然後執行以下操作任意次：

捕撈格子 (r, c) 處所有的魚，或者
移動到相鄰的水域格子。

請你返回漁夫最優策略下，最多可以捕撈多少條魚。如果沒有水域格子，請你返回 0 。

格子 (r, c) 相鄰的格子為 (r, c + 1) ，(r, c - 1) ，(r + 1, c) 和 (r - 1, c) ，前提是相鄰格子在網格圖內。

範例 1：

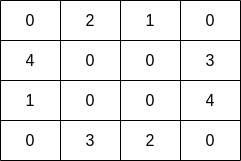
輸入：grid = [[0,2,1,0],[4,0,0,3],[1,0,0,4],[0,3,2,0]]
輸出：7
解釋：漁夫可以從格子(1,3) 出發，捕撈 3 條魚，然後移動到格子(2,3) ，捕撈 4 條魚。

範例 2：

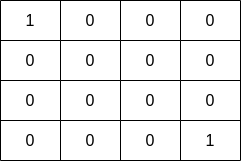
輸入：grid = [[1,0,0,0],[0,0,0,0],[0,0,0,0],[0,0,0,1]]
輸出：1
解釋：漁夫可以從格子 (0,0) 或者 (3,3) ，捕撈 1 條魚。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 10
0 <= grid[i][j] <= 10

問題抽象

求「加權連通分量 / 島嶼問題」，用二維 BFS 或 DFS 或並查集都可以求出所有連通塊的最大值，史上最水 Hard 題。

題解一（二維 DFS）

class Solution {

    private val directions = arrayOf(intArrayOf(0, 1), intArrayOf(0, -1), intArrayOf(1, 0), intArrayOf(-1, 0))

    fun findMaxFish(grid: Array<IntArray>): Int {
        var ret = 0
        for (i in 0 until grid.size) {
            for (j in 0 until grid[0].size) {
                ret = Math.max(ret, dfs(grid, i, j))
            }
        }
        return ret
    }

    private fun dfs(grid: Array<IntArray>, i: Int, j: Int): Int {
        if (grid[i][j] <= 0) return 0
        var cur = grid[i][j]
        grid[i][j] = -1
        for (direction in directions) {
            val newI = i + direction[0]
            val newJ = j + direction[1]
            if (newI < 0 || newI >= grid.size || newJ < 0 || newJ >= grid[0].size || grid[newI][newJ] <= 0) continue
            cur += dfs(grid, newI, newJ)
        }
        return cur
    }
}

複雜度分析：

時間複雜度：$O(n · m)$ 其中 n 和 m 是 grid 陣列的行和列；
空間複雜度：$O(n + m)$ 遞迴棧的最大深度。

題解二（並查集）

附贈一份並查集的解法：

class Solution {

    private val directions = arrayOf(intArrayOf(0, 1), intArrayOf(0, -1), intArrayOf(1, 0), intArrayOf(-1, 0))

    fun findMaxFish(grid: Array<IntArray>): Int {
        val n = grid.size
        val m = grid[0].size
        var ret = 0
        // 並查集
        val helper = UnionFind(grid)
        // 合併
        for (i in 0 until n) {
            for (j in 0 until m) {
                ret = Math.max(ret, grid[i][j])
                if (grid[i][j] <= 0) continue
                for (direction in directions) {
                    val newI = i + direction[0]
                    val newJ = j + direction[1]
                    if (newI < 0 || newI >= grid.size || newJ < 0 || newJ >= grid[0].size || grid[newI][newJ] <= 0) continue
                    ret = Math.max(ret, helper.union(i * m + j, newI * m + newJ))
                }
            }
        }
        // helper.print()
        return ret
    }

    private class UnionFind(private val grid: Array<IntArray>) {

        private val n = grid.size
        private val m = grid[0].size

        // 父節點
        private val parent = IntArray(n * m) { it }
        // 高度
        private val rank = IntArray(n * m)
        // 數值
        private val value = IntArray(n * m)

        init {
            for (i in 0 until n) {
                for (j in 0 until m) {
                    value[i * m + j] = grid[i][j]
                }
            }
        }

        // return 子集的和
        fun union(x: Int, y: Int): Int {
            // 按秩合併
            val parentX = find(x)
            val parentY = find(y)
            if (parentX == parentY) return value[parentY]
            if (rank[parentX] < rank[parentY]) {
                parent[parentX] = parentY
                value[parentY] += value[parentX]
                return value[parentY]
            } else if (rank[parentY] < rank[parentX]) {
                parent[parentY] = parentX
                value[parentX] += value[parentY]
                return value[parentX]
            } else {
                parent[parentY] = parentX
                value[parentX] += value[parentY]
                rank[parentY]++
                return value[parentX]
            }
        }

        fun print() {
            println("parent=${parent.joinToString()}")
            println("rank=${rank.joinToString()}")
            println("value=${value.joinToString()}")
        }

        private fun find(i: Int): Int {
            // 路徑壓縮
            var x = i
            while (parent[x] != x) {
                parent[x] = parent[parent[x]]
                x = parent[x]
            }
            return x
        }
    }
}

複雜度分析：

時間複雜度：$O(n · m)$ 其中 n 和 m 是 grid 陣列的行和列；
空間複雜度：$O(n + m)$ 遞迴棧的最大深度。

相似題目：

推薦閱讀：

如何使用並查集解決朋友圈問題？

Q4. 將陣列清空（Hard）

https://leetcode.cn/problems/make-array-empty/

題目描述

給你一個包含若干 互不相同 整數的陣列 nums ，你需要執行以下操作 直到陣列為空 ：

如果陣列中第一個元素是當前陣列中的 最小值 ，則刪除它。
否則，將第一個元素移動到陣列的末尾。

請你返回需要多少個操作使 nums 為空。

範例 1：

輸入：nums = [3,4,-1]
輸出：5

Operation	Array
1	[4, -1, 3]
2	[-1, 3, 4]
3	[3, 4]
4	[4]
5	[]

範例 2：

輸入：nums = [1,2,4,3]
輸出：5

Operation	Array
1	[2, 4, 3]
2	[4, 3]
3	[3, 4]
4	[4]
5	[]

範例 3：

輸入：nums = [1,2,3]
輸出：3

Operation	Array
1	[2, 3]
2	[3]
3	[]

提示：

1 <= nums.length <= 105
109 <= nums[i] <= 109
nums 中的元素 互不相同 。

預備知識 - 迴圈陣列

迴圈陣列：將陣列尾部元素的後繼視為陣列首部元素，陣列首部元素的前驅視為陣列尾部元素。

預備知識 - 樹狀陣列

OI · 樹狀陣列

樹狀陣列也叫二叉索引樹（Binary Indexed Tree），是一種支援「單點修改」和「區間查詢」的程式碼量少的資料結構。相比於線段樹來說，樹狀陣列的程式碼量遠遠更少，是一種精妙的資料結構。

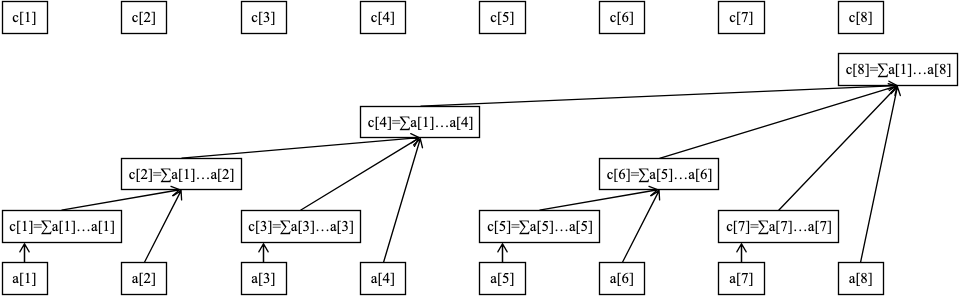
樹狀陣列核心思想是將陣列 [0,x] 的字首和拆分為不多於 logx 段非重疊的區間，在計算字首和時只需要合併 logx 段區間資訊，而不需要合併 n 個區間資訊。同時，在更新單點值時，也僅需要修改 logx 段區間，而不需要（像字首和陣列）那樣修改 n 個資訊。可以說，樹狀陣列平衡了單點修改和區間和查詢的時間複雜度：

單點更新 add(index,val)：將序列第 index 位元素增加 val，時間複雜度為 O(lgn)，同時對應於在邏輯樹形結構上從小分塊節點移動到大分塊節點的過程（修改元素會影響大分塊節點（子節點）的值）；
區間查詢 prefixSum(index)：查詢前 index 個元素的字首和，時間複雜度為 O(lgn)，同時對應於在邏輯樹形結構上累加區間段的過程。

樹狀陣列

問題結構化

1、概括問題目標

求消除陣列的操作次數。

2、分析題目要件

觀察：在每次操作中，需要觀察陣列首部元素是否為剩餘元素中的最小值。例如序列 [3,2,1] 的首部元素不是最小值；
消除：在每次操作中，如果陣列首部元素是最小值，則可以消除陣列頭部元素。例序列 [1,2,3] 在一次操作後變為 [2,3]；
移動：在每次操作中，如果陣列首部元素不是最小值，則需要將其移動到陣列末尾。例如序列 [3,2,1] 在一次操作後變為 [2,1,3]。

3、觀察資料特徵

資料量：測試用例的資料量上界為 10^5，這要求我們實現低於 O(n^2) 時間複雜度的演演算法才能通過；
資料大小：測試用例的資料上下界為 [-10^9, 10^9]，這要求我們考慮大數問題。

4、觀察測試用例

以序列 [3,4,-1] 為例，一共操作 5 次：

[3,4,-1]：-1 是最小值，將 3 和 4 移動到末尾後才能消除 -1，一共操作 3 次；
[3,4]：3 是最小值，消除 3 操作 1 次；
[4]：4 是最小值，消除 4 操作 1 次；

5、提高抽象程度

序列：線性表是由多個元素組成的序列，除了陣列的頭部和尾部元素之外，每個元素都有一個前驅元素和後繼元素。在將陣列首部元素移動到陣列末尾時，將改變陣列中的部分元素的關係，即原首部元素的前驅變為原尾部元素，原尾部元素的後繼變為原首部元素。
是否為決策問題：由於每次操作的行為是固定的，因此這道題只是純粹的模擬問題，並不是決策問題。

6、具體化解決手段

消除操作需要按照元素值從小到大的順序刪除，那麼如何判斷陣列首部元素是否為最小值？

手段 1（暴力列舉）：列舉陣列剩餘元素，判斷首部元素是否為最小值，單次判斷的時間複雜度是 O(n)；
手段 2（排序）：對原始陣列做預處理排序，由於原始陣列的元素順序資訊在本問題中是至關重要的，所以不能對原始陣列做原地排序，需要藉助輔助資料結構，例如索引陣列、最小堆，單次判斷的均攤時間複雜度是 O(1)。

如何表示元素的移動操作：

手段 1（陣列）：使用陣列塊狀複製 Arrays.copy()，單次操作的時間複雜度是 O(n)；
手段 2（雙向連結串列）：將原始陣列轉換為雙向連結串列，操作連結串列首尾元素的時間複雜度是 O(1)，但會消耗更多空間；

如何解決問題：

手段 1（模擬）：模擬消除和移動操作，直到陣列為空。在最壞情況下（降序陣列）需要操作 n^2 次，因此無論如何都是無法滿足題目的資料量要求；

至此，問題陷入瓶頸。

解決方法是重複「分析問題要件」-「具體化解決手段」的過程，列舉掌握的演演算法、資料結構和 Tricks 尋找突破口：

表示元素的移動操作的新手段：

手段 3（迴圈陣列）：將原陣列視為迴圈陣列，陣列尾部元素的後繼是陣列首部元素，陣列首部元素的前驅是陣列尾部元素，不再需要實際性的移動操作。

解決問題的新手段：

手段 2（計數）：觀察測試用例發現，消除每個元素的操作次數取決於該元素的前驅中未被消除的元素個數，例如序列 [3,4,-1] 中 -1 前有 2 個元素未被刪除，所以需要 2 次操作移動 3 和 4，再增加一次操作消除 -1。那麼，我們可以定義 rangeSum(i,j) 表示區間 [i,j] 中未被刪除的元素個數，每次消除操作只需要查詢上一次的消除位置（上一個最小值）與當前的消除位置（當前的最小值）中間有多少個數位未被消除 rangeSum(上一個最小值位置, 當前的最小值位置)，這個區間和就是消除當前元素需要的操作次數。

區分上次位置與當前位置的前後關係，需要分類討論：

id < preId：消除次數 = rangeSum(id, preId)
id > preId：消除次數 = rangeSum(-1, id) + rangeSum(preId,n - 1)

如何實現手段 2（計數）：

在程式碼實現上，涉及到「區間求和」和「單點更新」可以用線段數和樹狀陣列實現。樹狀陣列的程式碼量遠比線段樹少，所以我們選擇後者。

示意圖

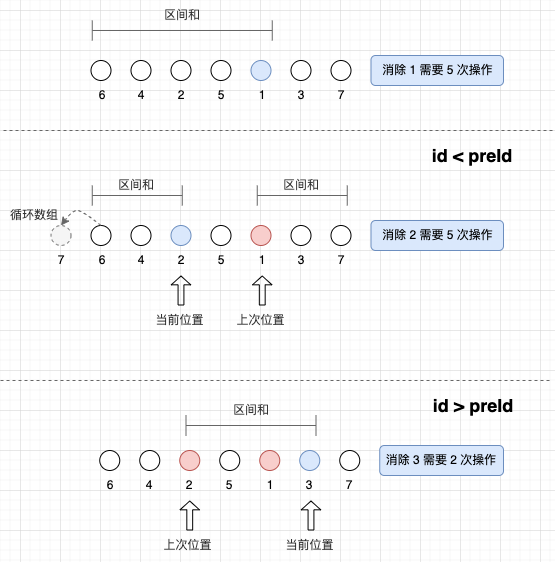
答疑：

消除每個元素的操作次數不用考慮前驅元素中小於當前元素的元素嗎？

由於消除是按照元素值從小到大的順序消除的，所以未被消除的元素一定比當前元素大，所以我們不強調元素大小關係。

題解一（樹狀陣列 + 索引陣列）

使用「樹狀陣列」的手段解決區間和查詢和單點更新問題，注意樹狀陣列是 base 1 的；
使用「索引陣列」的手段解決排序 / 最小值問題。

class Solution {
    fun countOperationsToEmptyArray(nums: IntArray): Long {
        val n = nums.size
        var ret = 0L
        // 索引陣列
        val ids = Array<Int>(n) { it }
        // 排序
        Arrays.sort(ids) { i1, i2 ->
            // 考慮大數問題
            // nums[i1] - nums[i2] x
            if (nums[i1] < nums[i2]) -1 else 1
        }
        // 樹狀陣列
        val bst = BST(n)
        // 上一個被刪除的索引
        var preId = -1
        // 遍歷索引
        for (id in ids) {
            // 區間和
            if (id > preId) {
                ret += bst.rangeSum(preId, id)
                // println("id=$id, ${bst.rangeSum(preId, id)}")
            } else {
                ret += bst.rangeSum(-1, id) + bst.rangeSum(preId, n - 1)
                // println("id=$id, ${bst.rangeSum(-1,id)} + ${bst.rangeSum(preId, n - 1)}")
            }
            // 單點更新
            bst.dec(id)
            preId = id
        }
        return ret
    }

    // 樹狀陣列
    private class BST(private val n: Int) {

        // base 1
        private val data = IntArray(n + 1)

        init {
            // O(nlgn) 建樹
            // for (i in 0 .. n) {
            //     update(i, 1)
            // }
            // O(n) 建樹
            for (i in 1 .. n) {
                data[i] += 1
                val parent = i + lowbit(i)
                if (parent <= n) data[parent] += data[i]
            }
        }

        fun rangeSum(i1: Int, i2: Int): Int {
            return preSum(i2 + 1) - preSum(i1 + 1)
        }

        fun dec(i: Int) {
            update(i + 1, -1)
        }

        private fun preSum(i: Int): Int {
            var x = i
            var sum = 0
            while (x > 0) {
                sum += data[x]
                x -= lowbit(x)
            }
            return sum
        }

        private fun update(i: Int, delta: Int) {
            var x = i
            while (x <= n) {
                data[x] += delta
                x += lowbit(x)
            }
        }

        private fun lowbit(x: Int) = x and (-x)
    }
}

複雜度分析：

時間複雜度：$O(nlgn)$ 其中 n 是 nums 陣列的長度，排序 $O(nlgn)$、樹狀陣列建樹 $O(n)$、單次消除操作的區間和查詢和單點更新的時間為 $O(lgn)$；
空間複雜度：$O(n)$ 索引陣列空間 + 樹狀陣列空間。

題解二（樹狀陣列 + 最小堆）

附贈一份最小堆排序的程式碼：

使用「樹狀陣列」的手段解決區間和查詢和單點更新問題，注意樹狀陣列是 base 1 的；
使用「最小堆」的手段解決排序 / 最小值問題。

class Solution {
    fun countOperationsToEmptyArray(nums: IntArray): Long {
        val n = nums.size
        var ret = 0L
        // 最小堆
        val ids = PriorityQueue<Int>() { i1, i2 ->
            if (nums[i1] < nums[i2]) -1 else 1
        }
        for (id in 0 until n) {
            ids.offer(id)
        }
        // 樹狀陣列
        val bst = BST(n)
        // 上一個被刪除的索引
        var preId = -1
        // 遍歷索引
        while (!ids.isEmpty()) {
            val id = ids.poll()
            // 區間和
            if (id > preId) {
                ret += bst.rangeSum(preId, id)
            } else {
                ret += bst.rangeSum(-1, id) + bst.rangeSum(preId, n - 1)
            }
            // 單點更新
            bst.dec(id)
            preId = id
        }
        return ret
    }
}

複雜度分析：

時間複雜度：$O(nlgn)$ 其中 n 是 nums 陣列的長度，堆排序 $O(nlgn)$、樹狀陣列建樹 $O(n)$、單次消除操作的區間和查詢和單點更新的時間為 $O(lgn)$；
空間複雜度：$O(n)$ 堆空間 + 樹狀陣列空間。

相似題目：

LeetCode 雙週賽 103（2023/04/29）區間求和的樹狀陣列經典應用

周賽概覽

Q1. K 個元素的最大和（Easy）

題目描述

預備知識 - 等差數列求和

題解（模擬 + 貪心）

Q2. 找到兩個陣列的字首公共陣列（Medium）

題目描述

題解一（雜湊表）

題解二（計數陣列）

題解三（狀態壓縮）

Q3. 網格圖中魚的最大數目（Hard）

題目描述

問題抽象

題解一（二維 DFS）

題解二（並查集）

Q4. 將陣列清空（Hard）

題目描述

預備知識 - 迴圈陣列

預備知識 - 樹狀陣列

問題結構化

1、概括問題目標

2、分析題目要件

3、觀察資料特徵

4、觀察測試用例

5、提高抽象程度

6、具體化解決手段

題解一（樹狀陣列 + 索引陣列）

題解二（樹狀陣列 + 最小堆）

往期回顧