2023 Hubei Provincial Collegiate Programming Contest題解 C F H I J K M
補題連結:https://codeforces.com/gym/104337
M. Different Billing
簽到題,寫幾個柿子然後列舉B或C即可。
#include <bits/stdc++.h>
#define int long long
using namespace std;
signed main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int x, y;cin >> x >> y;
for(int c = 0;c <= x; ++ c)
{
int b = (y - 2500 * c) / 1000;
if(b < 0 || 1000 * b + 2500 * c != y)continue;
int a = x - b - c;
if(a >= 0)
{
cout << a << ' ' << b << ' ' << c << '\n';
return 0;
}
}
cout << -1 << '\n';
return 0;
}
C. Darkness I
這題是對Minecraft中無限水的拓展過程為背景的一道思維題。
先考慮一下n, m均為奇數的情況:
然後從這種情況開始,增加一列,或者增加一行,都需要多加一個黑棋子,如果同時增加一行一列,那也是隻需要增加一個棋子,增加到右下角的位置即可。
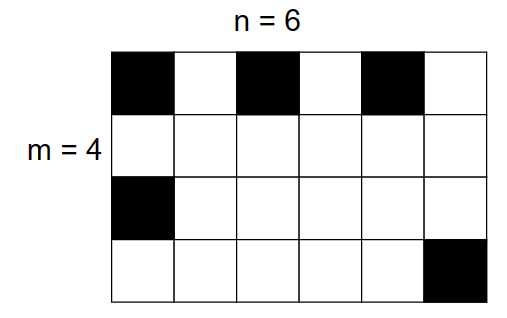
所以我們按照這種構造方法輸出答案即可。
#include <bits/stdc++.h>
#define int long long
using namespace std;
signed main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int n, m;cin >> n >> m;
int res = (n + 1) / 2 + (m + 1) / 2 - 1;
if(n % 2 == 0 || m % 2 == 0)res ++;
cout << res << '\n';
return 0;
}
J.Expansion
這題可以轉化為以下題意:
一開始身上資源為0,從1號點走到n號點,每個點上有一些資源(可能為負數),每秒鐘可以選擇走或者不走,且每秒會得到當前點上的資源(此時的資源已經做了字首和),為了保證每時每刻身上的資源都不為負數,請問從1走到n所需的最小時間。
我們模擬一下這個過程,如果到了某個點發現如果在當前點停留1秒會使得資源變為負數,就說明「我應該在左邊的某個正數點多停留一會兒」,而為了使得停留時間最少,我會選擇最大的點進行停留。
注意一些特判,題意需要保證最後在n一直停留都不會使得資源為負數,所以prefix[n]需要大於等於零,還有為了使得可以走到n,需要保證第一個非0的數為正數。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 9, p = 998244353;
int a[N], prefix[N];
signed main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int n;cin >> n;
for(int i = 1;i <= n; ++ i)cin >> a[i];
for(int i = 1;i <= n; ++ i)prefix[i] = prefix[i - 1] + a[i];
if(prefix[n] < 0)
{
cout << -1 << '\n';
return 0;
}
//遇到的第一個是負數
for(int i = 1;i <= n; ++ i)
{
if(prefix[i] != 0)
{
if(prefix[i] < 0)
{
cout << -1 << '\n';
return 0;
}
break;
}
}
int ans = 0, res = 0, mx = 0;
//前面一步步推進
for(int i = 1;i <= n; ++ i)
{
mx = max(mx, prefix[i]);
res += prefix[i];
ans ++;//走一秒
if(res < 0)//說明走快了,應該在前面多停留一段時間的
{
//補幾秒鐘
int ti = (-res + mx - 1) / mx;
ans += ti;
res += ti * mx;
}
}
cout << ans << '\n';
return 0;
}
H.Binary Craziness
賽時卡這道題了,一直在想拆位的做法(形成慣性思維了......糟糕)。
其實這題我們可以這樣想,最多m條邊,也就是所有點的出度之和一定是2m,然後我們最多n個點,也就是說出度的種類數不會超過 \(\sqrt{2m}\) 種。因為如果要使得種類數最多,那麼就是每一種都只有一個,且從小到大,出度陣列排序後(長度為t)將會是1, 2, 3, 4, 5, ...其和為\(\frac{t(t + 1)}{2} \le 2m\),所以長度t不會很大。
我們就可以根據這個原理做一個桶記錄一下某個數位出現的次數,然後直接雙重回圈暴力寫!
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 9, p = 998244353;
int cnt[2 * N], a[N];
int f(int x, int y)
{
return (x ^ y) * (x | y) * (x & y);
}
signed main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int n, m;cin >> n >> m;
for(int i = 1;i <= m; ++ i)
{
int x, y;cin >> x >> y;
a[x] ++, a[y] ++;
}
for(int i = 1;i <= n; ++ i)cnt[a[i]] ++;
vector<int> v;
for(int i = 1;i <= 2 * m; ++ i)if(cnt[i])v.push_back(i);
int res = 0;
for(int i = 0;i < v.size(); ++ i)
{
for(int j = i + 1;j < v.size(); ++ j)
{
res = (res + cnt[v[i]] * cnt[v[j]] % p * f(v[i], v[j]) % p) % p;
}
}
cout << res << '\n';
return 0;
}
F.Inverse Manacher
這題甚至不需要會馬拉車。
題目給定一個「迴文半徑」的陣列,要你還原還原出一種可能的字串(僅包含ab)。資料保證至少存在一種解。
只需要理解迴文半徑的含義即可。
當我們走到i時,如果a[i] > 1,說明我們要把i左邊的一部分堆成到右邊去,為了優化複雜度,我們可以用雙指標,r表示此時b陣列(也就是答案陣列)的大小,也就是我們更新到的右端,當r < i + a[i] - 1時,我們就拓展得到b[r],如果此時i > r,再根據一些情況來確定b[i]即可(交替的取a, b)。
注意陣列開大一點,馬拉車一般是兩倍空間。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 3e6 + 9;
int a[N];
char b[N];
signed main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int n;cin >> n;
for(int i = 0;i <= 2 * n + 1; ++ i)cin >> a[i];
char ch = 'a';
for(int i = 0, r = 0;i <= 2 * n + 1; ++ i)
{
while(i + a[i] - 1 > r)++ r, b[r] = b[2 * i - r];
if(i == 0)b[i] = '&';
else if(i & 1)b[i] = '|';
else if(b[i] == 0)b[i] = ch, ch = (ch == 'a' ? 'b' : 'a');
}
for(int i = 2;i <= 2 * n + 1;i += 2)cout << b[i];
return 0;
}
K.Dice Game
這題主要難在分析出n個事件相互獨立。
當x確定時,對於n個人當中的某一個人,他勝利的概率是\(p = \frac{m-x}{m-1}\),這個有兩種理解,第一個感性的理解就是,當投出y = x是沒有意義的,所以有效的y一共是m個,其中m - x個是可以贏的。
數學的理解是,這個人可能在第一次贏,也可能第二次贏,也可能第三次贏...,設平局概率為t,勝利概率為q。
其中\(t=\frac{1}{m}\), \(q = \frac{m-x}{m}\)。
根據等比數列求和我們可以知道:
然後對於某個x,一共有n個人,那麼答案就是\(p^n = (\frac{m-x}{m-1}) ^ n\)。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 9, p = 998244353;
int qmi(int a, int b)
{
int res = 1;
while(b)
{
if(b & 1)res = res * a % p;
a = a * a % p, b >>= 1;
}
return res;
}
int inv(int x){return qmi(x, p - 2);}
signed main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int n, m;cin >> n >> m;
int res = 1;
for(int i = 1;i <= m; ++ i)
{
cout << qmi((m - i) * inv(m - 1) % p, n) << ' ';
}
return 0;
}
I.Step
已知\(2t | k(k+1)\),求最小的\(k\),其中\(t=lcm(p_1,p_2...,p_n)\)。
不妨設\(2t=a*b\),且\(a|k,b|(k+1)\),且\(ax=k,by=(k+1)\),那麼我們可以得到:
轉換一下得到:
列舉a,可以算出b,然後exgcd搞出最小的x,即得到了k=ax答案。
現在問題是如何列舉a,我們看這個exgcd式子可以發現我們需要保證gcd(a, b) = 1,且有2t = a * b,所以我們可以對2t進行唯一分解,然後選取不同質因子種類分配給a和b。
分配方案可以通過二進位制直接做。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 9, inf = 8e18;
int p[N];
int gcd(int a, int b){return b == 0 ? a : gcd(b, a % b);}
int lcm(int a, int b){return a / gcd(a, b) * b;}
map<int, int> mp;
vector<int> v;
void func(int x)
{
for(int i = 2;i <= x / i; ++ i)
{
if(x % i)continue;
v.push_back(i);
mp[i] = 1;
while(x % i == 0)mp[i] *= i, x /= i;
}
if(x > 1)v.push_back(x), mp[x] = x;
}
int exgcd(int a, int b, int &x, int &y)
{
if(!b)return x = 1, y = 0, a;
int d = exgcd(b, a % b, y , x);
y -= a / b * x;
return d;
}
signed main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int n;cin >> n;
for(int i = 1;i <= n; ++ i)cin >> p[i];
int lc = p[1];
for(int i = 2;i <= n; ++ i)lc = lcm(lc, p[i]);
//對2 * lc進行質因數分解
func(2 * lc);
int res = inf;
for(int i = 0;i < (1ll << v.size()); ++ i)
{
//根據i得到a
int a = 1;
for(int j = 0;j < v.size(); ++ j)
if(i >> j & 1)a = a * mp[v[j]];
int b = 2 * lc / a;
int x, y, d = exgcd(a, b, x, y);
x = -x;
x = (x % (b / d) + (b / d)) % (b / d);
if(a * x)res = min(res, x * a);
//cout << "a = " << a << ' ' << "ax = " << a * x << '\n';
}
cout << res << '\n';
return 0;
}
