從不均勻性角度淺析AB實驗

作者：京東零售 路衛強

本篇的目的是從三個不均勻性的角度,對AB實驗進行一個認知的普及,最終著重講述AB實驗的一個普遍的問題，即實驗準確度問題。

一、AB實驗場景

在首頁中，我們是用紅色基調還是綠色基調，是採用門店小列表外+商品feed（左圖），還是採用門店大列表囊括商品feed（右圖），哪種更吸參照戶瀏覽下單呢，簡單來處理讓50%的使用者看到左圖效果，讓50%的使用者看到右圖效果，最終通過點選量，單量等指標進行比對得出結論，這是典型的AB實驗場景

二、AB實驗的定義

A/B實驗就是針對想迭代的產品功能，提供兩種不同的備選解決方案，然後讓一部分使用者使用方案A，另一部分使用者使用方案B，最終通過實驗資料對比來確定最優方案。

從定義裡我們就可以看出來,最直觀的一個概念,就是使用者的分流,此時就涉及到分流人數是否均勻的問題,即人數比例的均勻性。

三、AB中的三個不均勻

1、人數比例的不均勻

目前AB實驗的分流核心演演算法是通過的雜湊演演算法，假設我們按使用者名稱做為分流因子，使用murmurhash演演算法，以100桶製為例，確定一個人的位置的演演算法就是

//將使用者名稱通過hash演演算法計算出一個整數
int hashNum = MurmurHash3.murmurhash3_x86_32(useName)
//整數值對100取模
int bucket = hashNum % 100;

當我們定義一個實驗兩個策略的人數均為50%時，那麼

bucket為0-49的使用者由AB系統標記為A,業務系統根據A標記，使得使用者使用方案A

bucket為50-99的使用者由AB系統標記為B,業務系統根據B標記，使得使用者使用方案B。

可是我們都知道雜湊演演算法並不是絕對均勻的，當100人時，基本上不會出現有50個人走A，50個人走B，但是1萬個人的時候，兩部分流量可能就接近了1:1，10萬人的時候可能更接近1:1。

之前有位運營的同學問過，為什麼不能用一種很均勻的演演算法，比如第一個人來了，放入A，第二個人來了放入B，第三個人來了放入A，第四個人來了放入B....，這樣一天1W個人來，5000個取A策略，5000個取B策略。

假設我們真的這麼做了，第一天是OK的，第二天進A只來了4000人，這樣還是不均勻的，如果你第二天仍然按第一天的規則重新分配，這樣會有一部分人亂了策略，不符合我們固定人群走固定策略的實驗目的。

所以說這個不均勻是無解的，HASH演演算法是目前最理想的解決方案，前提是你需要一定的流量，流量越大，分流相對就比較準確。

2、人群素質的不均勻

我們假設流量足夠大，人數比例很均勻了，但是還有個問題就是人群素質的均勻問題。這裡的素質包括消費能力，活躍度，年齡等各種人群因素。

假設現在我們的活動統一採用的A策略（現狀），我們想驗證一下B策略（新策略）會不會帶來客單價的提升，就直接做了AB實驗，還按1:1比例來分流，發現使用A方案的人群客單價是100，使用客單價B的人群是96，此時我們能認為原有A方案優於B方案嗎？其實是不能的，怎樣確定這種人群素質的差異呢，可以採用AA實驗，就是兩部分人都走A，進行分開統計，可能會發現，位於0-49桶的人群本身客單價就是100，而位於50-99桶的人群可能只有94，這麼看來B方案是能提升客單價的，因為位於50-99桶的人群本身指標就差一些。

當然AA不是必須的，可能你有整體的客單價指標，上了B策略後發現整體提升了，這種情況相當於灰度驗證了，但實際情況是比較複雜的，整體指標你是不清楚的（因為這裡的整體可能只是你取的業務中的一部分流量）。

所以解決素質不均勻的手段就是採用AA提前確定差異性，再在這個差異性基礎上看差異的變化。

3、實驗間影響的不均勻

這個不均勻性是最複雜的，一般做實驗我們走兩種極端：

第一種是完全不復用人群，每個實驗人群都是獨立的，這樣的話效果比較準確，但是弊端是，當所有流量都被用去後，不能有新實驗開始，必須等待有結束的實驗後才能繼續做。

第二種，所有實驗都用全部流量，此時我們認為實驗雖然互相之間有影響，但是這種影響是正交的，量大的時候應該是均勻的，如下圖所示，P實驗的兩個策略人群，到Q實驗時，對Q的兩個策略影響是均勻的。

這種可以滿足無限個實驗，想做多少實驗都可以，但弊端是，實驗太多，必然有影響不均勻的，且我們無法消除這種不均勻。

所以我們想能不能結合以上兩種情況來處理呢，結合google的Overlapping Experiment Infrastructure文章我們設計出分層的實驗管理模型

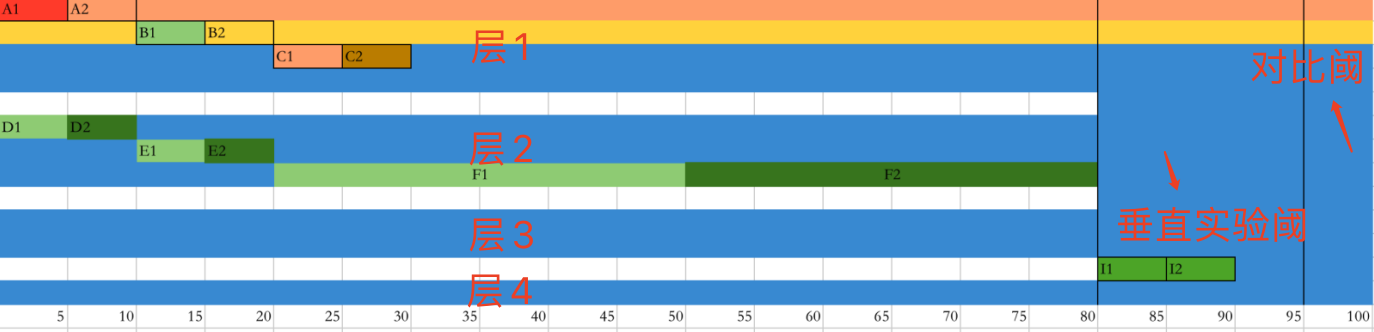
首先我們將總流量分成兩部分，正交域，垂直域（含對比區）

我們假設如圖取80%的流量用做正交閾，20%用作垂直域，垂直域中有5%用做對比區。

上圖正交域下4個層，層內實驗流量互斥，層間實驗流量正交，我們將可能會互相影響的實驗放到同一層內進行流量互斥，而影響不大的實驗可以放到不同層內。

垂直域中的實驗流量只能互斥，且不與任何實驗正交，可以理解用最純正的流量做實驗，可以I1和I2兩個策略間對比，也可以I1或I2和對比域（現狀）比對。

那此時有一個很重要的問題需要解決，我們怎麼確定哪些實驗互相影響較大，需要放到同一層下。

有一些簡單標準，比如入口不一樣，目標不一樣等等，這種可以放到不同層，我們可以忽略正交不均勻的問題，反之就不行。

比如活動頁劵對單量提升度的實驗和會員頁面入會效果的實驗，就可以放到不同層。

而首頁上滿減活動實驗對客單價提升的實驗和同樣首頁買贈活動對客單價提升的實驗，最好是不共用使用者，放到同層比較合適。

但對於很多實驗是不太容易通過簡單規則來確定的，需要巨量資料的同學和產品，甚至研發來共同決定實驗放到哪些層和哪些實驗互斥，這確實在實際的運作中是最難的點。

總之採用這種策略，可以複用流量的同時還可以降低不必要的互相影響，比較綜合考慮了流量和準確度問題。

四、總結

現在我們對以上問題進行總結，從問題到解決方案上來認識ab實驗

1、人群做不到絕對的均勻，只能通過HASH演演算法，結合一定的流量來解決。

2、通過AA實驗，來提前確定人群素質的不均勻。最終的實驗資料結合AA實驗資料來確定最終效果。

3、設計出正交垂直域，正交閾內多個層，每個層內放可能相互影響的實驗，層內互斥，層間正交，保留垂直域，為要求精準的實驗留出流量，來解決實驗間相互影響的問題。

本篇從核心分流與實驗間相互影響角度講解ab實驗，希望能引起大家在做實驗前能有更多的思考，來更準確的驗證自己想要的效果，希望大家有興趣的可以留言討論。