【LeetCode動態規劃#14】子序列系列題(最長遞增子序列、最長連續遞增序列、最長重複子陣列、最長公共子序列)
最長遞增子序列
給你一個整數陣列 nums ,找到其中最長嚴格遞增子序列的長度。
子序列是由陣列派生而來的序列,刪除(或不刪除)陣列中的元素而不改變其餘元素的順序。例如,[3,6,2,7] 是陣列 [0,3,1,6,2,2,7] 的子序列。
範例 1:
- 輸入:nums = [10,9,2,5,3,7,101,18]
- 輸出:4
- 解釋:最長遞增子序列是 [2,3,7,101],因此長度為 4 。
範例 2:
- 輸入:nums = [0,1,0,3,2,3]
- 輸出:4
範例 3:
- 輸入:nums = [7,7,7,7,7,7,7]
- 輸出:1
提示:
- 1 <= nums.length <= 2500
- -10^4 <= nums[i] <= 104
思路
什麼是"最長遞增子序列"?
以 nums = [1,8,3,2,5,6,7,9] 為例
[1,8]是nums中的一個"遞增子序列",[3,5,6]是另一個"遞增子序列",且後者更長
由上述例子可知,子序列的選取可以不連續,但必須按照陣列原有順序來取(意思就是可以在原有順序上跳過某些數從而構成更長的子序列)
基於此原則,上述例子中的"最長遞增子序列"是[3,5,6,7,9]
明確這一點後,可以開始討論解題方法
五步走
1、2 確定dp陣列含義+確定遞推公式
dp[i]: 以nums[i]為結尾的最長遞增子序列的長度
這麼理解呢?
舉個例子,nums = [1,8,3,2,5,6]
遍歷時是用雙指標去實現子序列的查詢的,因此還需要一個指標j用來遍歷區間內的所有元素,尋找該區間內最長的子序列
假設j是小於i的,那麼兩者構成的區間就是[j,i]
此時就有dp[j] < dp[i],即以nums[0]為結尾的最長遞增子序列(即[1])小於以nums[1]為結尾的最長遞增子序列(即[1,8])
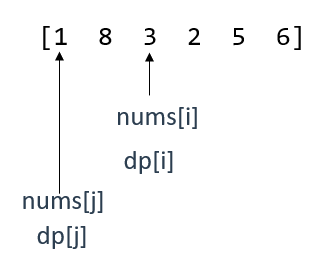
此時,指標i向後移動,j也繼續在[j,i]範圍內遍歷,當遍歷到以下位置時,可以找到推匯出dp[i]的前置位置
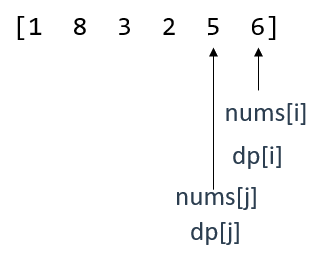
當前,dp[j]仍小於dp[i](len[1,3,5] < len[1,3,5,6]),根據dp陣列的定義,dp[j]是"長度"。
就這個層面而言,dp[i]與dp[j]的長度差距為1,所以有dp[i] = dp[j] + 1;
上面說過,指標j是在[j,i]範圍內從左向右遍歷,目的是尋找子序列
因此每次遍歷都會得到一個新的dp[i]
所以遞推公式應該是:dp[i] = max(dp[i], dp[j] + 1);
這裡解釋一下在遍歷過程中,子序列是如何定義的,以及我們比較dp[i]和dp[j]到底在比較什麼東西
因為i和j都是從左往右遍歷,所以每次迴圈以nums[i]和以nums[j]為結尾的最長遞增子序列都有可能更新
不同的是,指標j的遍歷範圍是約束在[j,i]之內的
每次遍歷完[j,i]之內的所有子序列nums[j]後,才會移動i去擴大區間
詳見:單詞拆分的遍歷過程
3、初始化dp陣列
根據dp陣列的含義,我們求的是以nums[i]為結尾的最長遞增子序列的長度
不管i是多少,其子序列至少包括nums[i],也就是說長度至少為1
所以dp[i]全部初始化為1即可
4、確定遍歷順序
這裡從左往右或者從右往左遍歷其實都行
特別注意的一點是最後的返回值
通常我們都是返回dp陣列的最後一個值,即dp[nums.size() - 1]
但這裡不行
以題目給的範例1來說
範例 1:
- 輸入:nums = [10,9,2,5,3,7,101,18]
- 輸出:4
- 解釋:最長遞增子序列是 [2,3,7,101],因此長度為 4
這裡最後遍歷到101(即dp[6])時,取到最長嚴格遞增子序列
顯然這不是dp陣列的最後一個值
因此我們需要設定一個變數,在迴圈過程中不斷更新最長的子序列長度,最後返回這個最大值
為什麼這裡最長遞增子序列是 [2,3,7,101] 而不可以是 [2,3,7,18]?
實際上確實也可以是後者,但我推測可能是題目中的最長"嚴格遞增"子序列長度做出了限制
程式碼
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
if (nums.size() <= 1) return nums.size();
//定義並初始化dp陣列
vector<int> dp(nums.size(), 1);
//結果變數res
int res = 1;//注意,至少長度為1,因此res要初始化為1
//遍歷dp陣列
for(int i = 1; i < nums.size(); ++i){
for(int j = 0; j < i; ++j){//當nums[i] > nums[j]時不斷遍歷[j,i]範圍內的子序列
if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
//不滿足條件就移動i擴大範圍
}
if(dp[i] > res) res = dp[i];//更新更長的子序列長度
}
return res;
}
};
最長連續遞增序列
給定一個未經排序的整數陣列,找到最長且 連續遞增的子序列,並返回該序列的長度。
連續遞增的子序列 可以由兩個下標 l 和 r(l < r)確定,如果對於每個 l <= i < r,都有 nums[i] < nums[i + 1] ,那麼子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是連續遞增子序列。
範例 1:
- 輸入:nums = [1,3,5,4,7]
- 輸出:3
- 解釋:最長連續遞增序列是 [1,3,5], 長度為3。儘管 [1,3,5,7] 也是升序的子序列, 但它不是連續的,因為 5 和 7 在原陣列裡被 4 隔開。
範例 2:
- 輸入:nums = [2,2,2,2,2]
- 輸出:1
- 解釋:最長連續遞增序列是 [2], 長度為1。
提示:
- 0 <= nums.length <= 10^4
- -10^9 <= nums[i] <= 10^9
思路
由題意,與上題最大的不同是這裡要求子序列是連續的,不能跳
五步走
1、確定dp陣列含義
dp[i]:以下標i為結尾的連續遞增的子序列長度為dp[i]
2、確定遞推公式
根據題目的條件,連續遞增的子序列要滿足 nums[i] < nums[i + 1]
也就是說,如果 nums[i] > nums[i - 1],那麼以 i 為結尾的連續遞增的子序列長度 一定等於 以i - 1為結尾的連續遞增的子序列長度 + 1
所以遞推公式為:dp[i] = dp[i - 1] + 1;
因為本題要求連續遞增子序列,所以不用去比較nums[j]與nums[i] (j在0到i之間遍歷)
既然不用j了,那麼也不用兩層for迴圈,本題一層for迴圈就行,比較nums[i] 和 nums[i - 1]。
3、初始化dp陣列
與上一題一樣,dp[i]長度至少為1(即包含本身),因此dp陣列初始化為1即可
4、確定遍歷順序
從遞推公式看,dp[i]依賴dp[i - 1],因此應該從前向後遍歷
程式碼
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
//處理異常
if(nums.size() == 0) return 0;
//定義並初始化dp陣列
vector<int> dp(nums.size(), 1);
int res = 1;//注意,至少長度為1,因此res要初始化為1
//遍歷dp陣列
for(int i = 1; i < nums.size(); ++i){
//子序列還滿足遞增趨勢時執行下面的語句
if(nums[i] > nums[i - 1]) dp[i] = dp[i - 1] + 1;
if(dp[i] > res) res = dp[i];
}
return res;
}
};
最長重複子陣列
給兩個整數陣列 A 和 B ,返回兩個陣列中公共的、長度最長的子陣列的長度。
範例:
輸入:
- A: [1,2,3,2,1]
- B: [3,2,1,4,7]
- 輸出:3
- 解釋:長度最長的公共子陣列是 [3, 2, 1] 。
提示:
- 1 <= len(A), len(B) <= 1000
- 0 <= A[i], B[i] < 100
思路
這裡要求兩個陣列中最長重複子陣列,其實就是要在兩個陣列中找到最長的公共子序列
並且這裡的子序列應該要求是連續的,也就是和 最長連續遞增序列 的要求類似
所以我們可以仿照著去定義dp陣列,但因為涉及兩個陣列,所以dp陣列應該也要是二維的
五步走
1、確定dp陣列含義
有兩個陣列nums1、nums2,那麼自然需要兩個指標用於遍歷,分別是i、j
這兩個指標應該是同步移動的,其指向的分別為:nums1和nums1中,當前子陣列(子序列)的末尾

如上圖所示,指標i、j再往後移一次就不滿足重複子陣列的條件了,因此上述兩個陣列的最長重複子陣列就是[1,8,3]
dp[i][j]:nums1中以下標為 i - 1 和nums2中以下標為 j - 1 的最長重複子陣列長度為dp[i][j]
這裡為什麼不從i和j開始?要減1呢?
實際上是一個優化技巧,如果從i、j開始,在初始化dp陣列時還要單獨為
dp[i][0]和dp[0][j]進行初始化,但其實這是沒有必要的
2、確定遞推公式
dp[i][j]的狀態是由dp[i - 1][j - 1]推匯出來的
正確的理解思路是如下(還是拿上面的圖來說)
我們要找的是存在於nums1、nums2中的最長公共子陣列
當前i、j下標指向的值之前區間構成的子陣列如果是nums1、nums2中公共的(相同的),那麼滿足條件,dp陣列記錄當前長度
i、j同時向後移動;如果不相同,dp陣列不記錄長度(保持為初始值),i、j仍同時向後移動
根據dp陣列的定義,dp[i][j]是在下標i - 1 和 j - 1時找到的最長公共子陣列的狀態
因此,dp[i][j]的前置狀態應該也要是找到對應下標下的最長公共子陣列的狀態,即dp[i - 1][j - 1],而這兩個狀態在"陣列長度"層面相差1,所以要用dp[i - 1][j - 1]推匯出dp[i][j]就要加1
綜上,本題的遞推公式為: dp[i][j] = dp[i - 1][j - 1] + 1
(其實和上題的分析過程類似)
3、初始化dp陣列
這裡,因為之前在定義dp陣列時,我們選擇了從 i - 1 和 j - 1 開始
所以,根據dp陣列含義,dp[i][0]和dp[0][j]是沒有意義的,因為我們是從 i - 1 和 j - 1 開始找(從i=1,j=1開始遍歷),所以沒必要初始化這倆
如果從i、j開始,那麼
dp[i][0]和dp[0][j]就是有意義的,我們需要遍歷nums1、nums2來初始化(儘管可能初始化的值很怪)
雖然沒有意義,但是肯定還是要有個初始值的,0在合適不過了
即,dp[i][0] = 0、dp[0][j] = 0
其他部分可以初始化為任意值(原因詳見),為了統一,也初始化為0
4、確定遍歷順序
從前向後遍歷,原因說過很多次了,即i的狀態需要根據i - 1推導
然後先遍歷nums1、nums2都無所謂(長度一樣)
程式碼
class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2) {
// 建立並初始化dp陣列
// vector<vector<int>> dp(nums1.size(), vector<int>(nums2.size(), 0));//錯誤
vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
int res = 0;
//遍歷dp陣列
for(int i = 1; i <= nums1.size(); ++i){//注意邊界條件,小於等於
for(int j = 1; j <= nums2.size(); ++j){//小於等於
//為了與dp陣列的定義保持一致,這裡要用i - 1和j - 1為下標進行比較
if(nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
if(dp[i][j] > res) res = dp[i][j];
}
}
return res;
}
};
注意事項 TBD
以下程式碼中,為什麼建立dp陣列時,nums1.size() + 1
class Solution {
public:
int findLength(vector
//建立並初始化dp陣列
vector<vector
int res = 0;
//遍歷dp陣列
for(int i = 1; i <= nums1.size(); ++i){
for(int j = 1; j <= nums2.size(); ++j){
if(nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
if(dp[i][j] > res) res = dp[i][j];
}
}
return res;
}
};
最長公共子序列
給定兩個字串 text1 和 text2,返回這兩個字串的最長公共子序列的長度。
一個字串的 子序列 是指這樣一個新的字串:它是由原字串在不改變字元的相對順序的情況下刪除某些字元(也可以不刪除任何字元)後組成的新字串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。兩個字串的「公共子序列」是這兩個字串所共同擁有的子序列。
若這兩個字串沒有公共子序列,則返回 0。
範例 1:
輸入:text1 = "abcde", text2 = "ace" 輸出:3 解釋:最長公共子序列是 "ace",它的長度為 3。
範例 2: 輸入:text1 = "abc", text2 = "abc" 輸出:3 解釋:最長公共子序列是 "abc",它的長度為 3。
範例 3: 輸入:text1 = "abc", text2 = "def" 輸出:0 解釋:兩個字串沒有公共子序列,返回 0。
提示:
- 1 <= text1.length <= 1000
- 1 <= text2.length <= 1000 輸入的字串只含有小寫英文字元
思路
與上題的區別是,這題又可以使用不連續但符合原有相對順序的子序列了
開始分析
五步走
1、確定dp陣列含義
這裡要從兩個字串陣列裡去找公共子序列,因此仍然需要使用二維dp陣列
dp[i][j]:下標為i - 1和j - i時,對於兩個陣列而言的最長公共子序列的長度為dp[i][j]
(長度為[0, i - 1]的字串text1與長度為[0, j - 1]的字串text2的最長公共子序列為dp[i][j])
為什麼要減1?為了避免初始化dp[i][0]和dp[0][j],詳見上一題
2、確定遞推公式
因為允許有不連續的子序列,所以這裡會有多種情況
(1)如果當前的text1[i] == text2[j]
那沒什麼好說的,和上題的推導一模一樣,dp[i][j] = dp[i - 1][j - 1] + 1
(2)除了相等以外的其他情況
這裡用題目給的範例1來說明

因為text2就那麼長,所以遍歷到黑線處就結束了,那就以這個位置舉例說明(遍歷到前一個位置時分析同理)
需要明確一下,當前情況下,我們是在[a,b,c] (text1)和[a,c,e] (text2) 中找公共子序列
當遍歷到如上圖中位置時,i指向text1的'c',j指向text2的'e',這兩個字元顯然不相等,因此無法觸發情況1
此時有兩種情況可以考慮,因為'c'和'e'已經不相等了,那就看其前面一位,看看剩下的還能不能構成公共子序列
情況1:text1退回一位
a b c
↑
i
a c e
↑
j
現在[a,b,c] (text1)和[a,c,e] (text2) 的最長公共子序列長度是1([a])
情況2:text2退回一位
a b c
↑
i
a c e
↑
j
由於可以有不連續子序列,所以[a,b,c] (text1)和[a,c,e] (text2) 的最長公共子序列長度是2([a,c])
顯然,要從這兩種情況中取較大的那個
綜上,除了text1[i] == text2[j]以外的其他情況時的遞推公式是:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
因此,本題的遞推公式完整寫法如下:
if (text1[i - 1] == text2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
3、初始化dp陣列
首先,空串的子序列長度為0
然後就是text1[i - 1]和text2[j - 1],上題說過,這倆初始化沒有意義,但是還是要給個值,為了統一就給0
然後其他部分可任意初始化,為了統一也給0
4、確定遍歷順序

如上圖所示,我們有三個方向可以推到dp[i][j],因此遍歷順序應該是從前往後,從上到下
(詳見二維揹包推導)
程式碼
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
//定義dp陣列並初始化
vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));
int res = 0;
//遍歷dp陣列
for(int i = 1; i <= text1.size(); ++i){//注意邊界條件,小於等於
for(int j = 1; j <= text2.size(); ++j){//小於等於
if(text1[i - 1] == text2[j - 1]){//為了與dp陣列的定義保持一致,這裡要用i-1和j-1為下標進行比較
dp[i][j] = dp[i - 1][j - 1] + 1;
}else{
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
if(dp[i][j] > res) res = dp[i][j];
}
}
return res;
}
};