論文資訊

論文標題：MEnsA: Mix-up Ensemble Average for Unsupervised Multi Target Domain Adaptation on 3D Point Clouds
論文作者：Ashish Sinha, Jonghyun Choi
論文來源：2023 CVPR
論文地址：download 
論文程式碼：download
視屏講解：click

1 前言

　　單目標域和多目標域

2 介紹

　　單目標域和多目標域的差異：

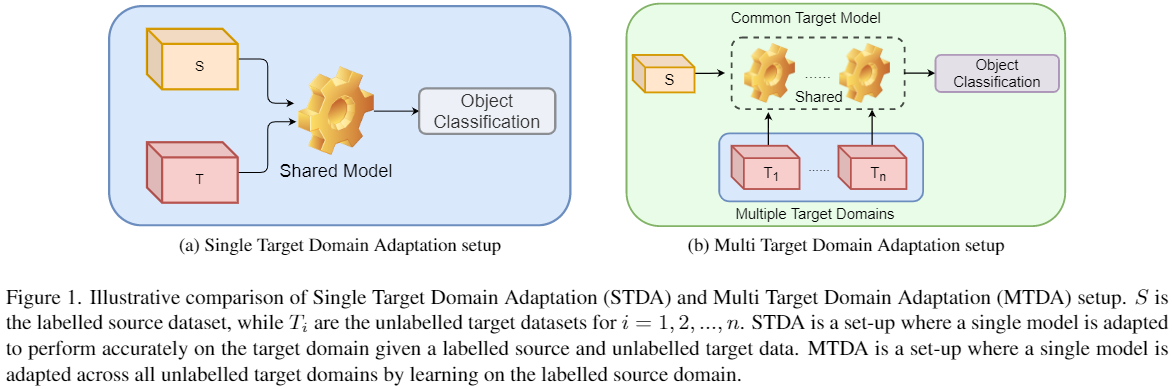
3 方法

3.1 整體框架

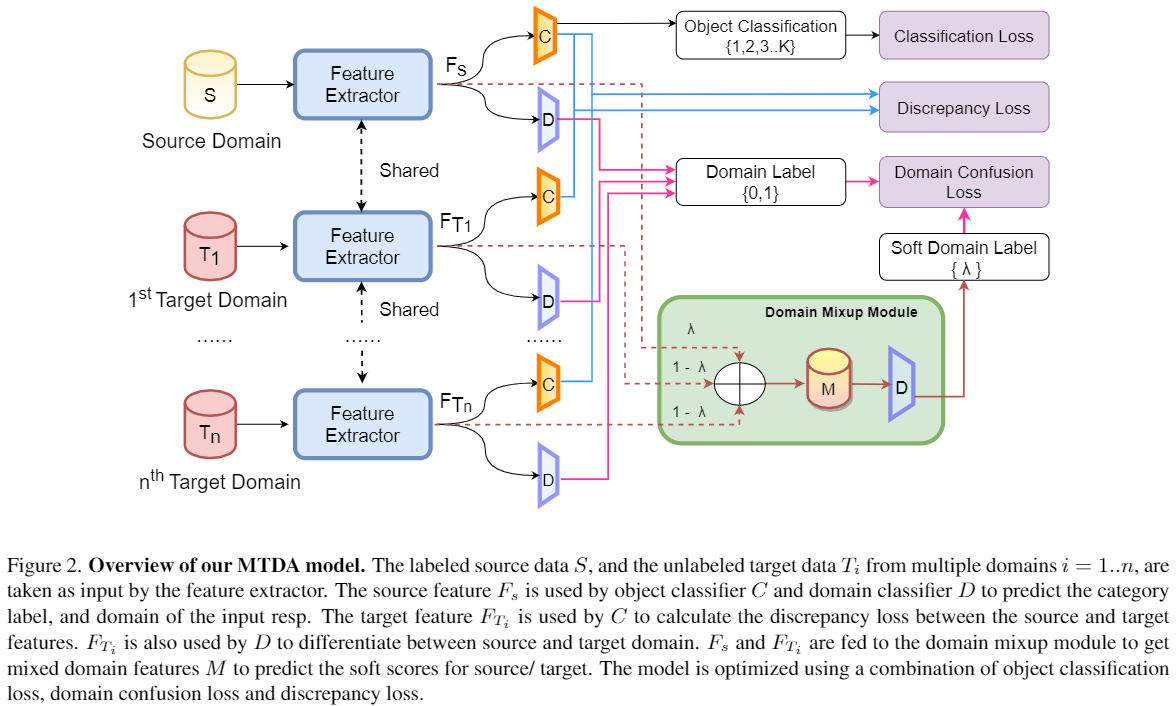
3.2 域 mixup 模組

　　Mixup 模組：

　　　　$F_{i}^{m}=\lambda F_{s}+(1-\lambda) F_{T_{i}}  \quad\quad(1)$

　　　　$L_{i}^{m}=\lambda L_{s}+(1-\lambda) L_{T_{i}}   \quad\quad(2)$

　　線性差值的好處：

• • 有助於建立一個連續域不變的潛在空間，使混合特徵能夠對映到源域和目標域的潛在空間之間的位置，這種連續的潛在空間對於跨多個域的域不變推理至關重要；
  • 作為一個有效的正則化器，幫助領域分類器 $D$ 在預測混合特徵嵌入 $F_{mi}$ 的領域(源或目標) 的軟分數方面有所提高；

3.3 對比

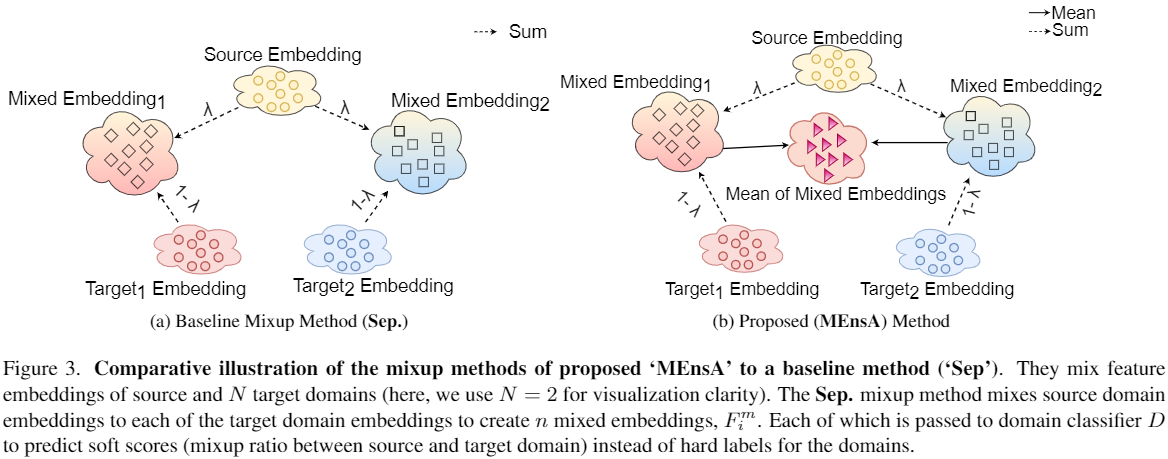
　　基線：【多目標域場景下】

• • 形式：單源域和單目標域線性差值；
  • 問題：存在災難性遺忘問題，只專注於學習源域和一個目標域之間的域不變特徵，忽略了跨多個域的共用特徵；

　　本文：單源域 和 多目標域整合線性差值；

• • 形式：$F_{m}^{M}=\frac{1}{n} \sum_{i=1}^{n} F_{i}^{m}  \quad\quad(3)$；
  • 目的：旨在捕獲跨多個域共用的域不變特徵，減輕域間的衝突資訊，提高泛化性；

3.4 訓練目標

　　總損失：

　　　　$\mathcal{L}=\log \left(\sum\left(e^{\gamma\left(\mathcal{L}_{c l s}+\eta \mathcal{L}_{d c}+\zeta \mathcal{L}_{a d v}\right)}\right)\right) / \gamma  \quad\quad(4)$

　　其中：

　　　　源域分類損失： $\mathcal{L}_{c l s}  =\mathcal{L}_{C E}\left(C\left(F_{s}\right), y_{s}\right)  \quad\quad(4)$

　　　　單源域單目標域鑑別損失：$\mathcal{L}_{d c}  =\mathcal{L}_{C E}\left(D\left(F_{s}\right), L_{s}\right)+\mathcal{L}_{C E}\left(D\left(F_{T_{i}}, L_{T_{i}}\right)\right)    \quad\quad(5)$

　　　　對抗損失：$\mathcal{L}_{a d v} =\lambda_{1} \mathcal{L}_{m m d}+\lambda_{2} \mathcal{L}_{d c}+\lambda_{3} \mathcal{L}_{\text {mixup }}  \quad\quad(6)$

　　關於對抗損失：

　　　　MMD 損失：$\mathcal{L}_{m m d}=\mathcal{L}_{r b f}\left(C\left(F_{s}\right), F_{T_{i}}, \sigma\right)    \quad\quad(7)$

　　　　線性差值域鑑別損失：$\mathcal{L}_{\text {mixup }}=\mathcal{L}_{C E}\left(D\left(F_{m}^{M}\right), L_{i}^{m}\right)  \quad\quad(8)$ 

　Note：

　　線性差值：

　　　　$F_{m}^{\text {factor }}=\lambda F_{s}+\sum_{i=1}^{n} \frac{1-\lambda}{n} F_{T_{i}}$

　　　　$F_{m}^{\text {concat }}=\left[\lambda F_{s}, \frac{1-\lambda}{n} F_{T_{1}}, \ldots, \frac{1-\lambda}{n} F_{T_{n}}\right]$

　　　　$.L_{m}^{\text {concat }}=[\lambda, 2 \frac{1-\lambda}{n}, \ldots, N \frac{1-\lambda}{n}]$

　　　　$F_{m}^{T}=\lambda F_{T_{1}}+(1-\lambda) F_{T_{2}}$

　　　　$L_{m}^{T}=\lambda L_{T_{1}}+(1-\lambda) L_{T_{2}} $