本文對插值、平穩假設、變異函數、克里格等常用的地學計算概念加以介紹，並對相關公式進行推導。

1 引言

  最近的幾篇部落格，分別從遙感的實際應用出發，對影像前期處理與相關演演算法、反演操作等加以詳細介紹。而通過遙感手段獲取了豐富的各類地表資訊資料後，如何對資料加以良好的數學處理與科學分析，同樣是我們需要重視的問題。因此，準備由這一篇部落格入手，逐篇地對地學計算方面的內容加以初步總結。

  那麼首先，我們就由地學計算的幾個基本概念入手，對相關理論方面的內容加以一定了解。

  需要注意的是，以下內容如果單獨來看或許有些不好理解，但一旦將其與實際應用結合，便會豁然開朗。其中，具體的實際應用部分我將會在後面的部落格中涉及。

2 空間插值

  空間資料的獲取是進行空間分析的基礎與起源。為了提高研究結論的精度，我們亦總是希望能夠獲取研究區域內更多、更全面的精確空間屬性資料資訊。然而，在實際研究、工作中，由於人力、成本、資源等外部條件限制，我們不可能對全部未知區域加以取樣與測量，而往往只能得到研究區域內有限數量的取樣點及其相關屬性資料。因此，往往可以考慮選取合適的空間取樣點，利用一定數學模型，依據已知取樣點各自對應屬性資料對研究區域所有位置的未知屬性資訊加以預測。

  空間插值（Spatial Interpolation）即可以實現這一需求。其是一種將離散取樣點測量資料轉換為連續資料曲面的常用方法，包括內插（Interpolation）和外推（Extrapolation）兩種應用形式。一般地，對樣本點範圍以內（即所有取樣點最大外接矩形內部）的空間進行插值，才可稱作「內插」（部分文獻亦直接用「插值」代替「內插」）；反之則稱「外推」或「預測」，往往認為外推的結果誤差較大。

  空間插值理論及其方法基於著名的「地理學第一定律（Tobler's First Law of Geography）」，即一般地，距離越近的地物具有越高的相關性。這一至今已產生深遠影響的地學定律最早由美籍瑞士地理學家Waldo R. Tobler教授於1970年提出。

  在各方法所對應的數學計算原理層面，空間插值一般可以分為確定性插值方法（Deterministic Interpolation）與地統計插值方法（Geostatistics，亦稱非確定性插值方法）兩種。其中，確定性插值方法基於研究區域內各資訊點之間相似程度或整個曲面的平滑程度，從而建立連續的擬合曲面；其依據插值計算時納入考慮的取樣點分佈範圍，又可進一步分為整體插值法與區域性插值法。地統計插值方法則是基於研究區域內各資訊點的綜合統計學規律，以變異函數（Variogram）理論與結構分析為基礎，實現其屬性的空間自相關性定量化，從而建立得出連續插值曲面。

  在所建立連續插值表面通過全部取樣點的與否層面，空間插值一般又可以分為精確性插值與非精確性插值兩種。其中，前者預測樣點的屬性數值與其各自實測值相等，即其取樣點屬性資料全部落入預測結果曲面；後者預測樣點的屬性數值則往往不與其各自實測值相等，即其取樣點屬性資料一般不會落入預測結果曲面。因此，使用非精確性插值方法往往可以避免在預測表面中出現明顯的波峰或波谷，整體呈現出平緩態勢。

3 幾個重要假設

  地學計算中，幾個重要假設可以說是關鍵中的關鍵；而其往往也比較難以理解，不怕，我們慢慢往下看。

3.1 平穩假設

  平穩假設（Stationary Assumption）是指，一組觀測值的均值是始終固定的，其與觀測值所在位置無關；將既定的某個點集由某一研究區域內某處移動至另一處時，隨機函數的性質保持不變。即隨機函數的分佈規律不因位置的改變而改變，具有嚴格的平穩性。平穩性假設的公式表達為：

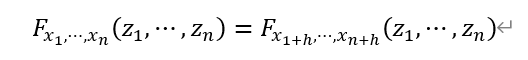
  其中，F_(x_1,⋯,x_n ) (z_1,⋯,z_n )表示位置在(x_1,⋯,x_n )上的點集(z_1,⋯,z_n )對應的隨機函數。

3.2 二階平穩性假設

  二階平穩性假設（Second Stationary Assumption）又稱弱平穩假設，其與協方差函數（Covariance Function）有關。這一假設認為，隨機函數的均值為一常數，且任意兩個隨機變數之間的協方差僅僅依賴於其二者之間的距離與方向，而與其具體位置無關。

  將上述兩個條件用公式分別表達為：

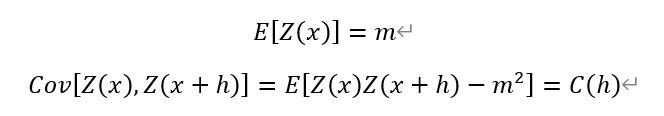
  其中，E[Z(x)]為區域化變數Z(x)的數學期望， Cov[Z(x),Z(x+h)]為區域化變數Z(x)與Z(x+h)所對應的協方差函數，C(h)為僅與h有關的協方差取值，m為一常數，h為滯後距。

  上述二階平穩性假設是針對整個研究區域範圍而言。若區域化變數僅僅在整個研究區域內的某個有限區域中滿足上述條件，即條件僅在區域性區域成立，則稱此區域化變數滿足準二階平穩性假設（Quasi Second Stationary Assumption）。準二階平穩性假設可以視作一種折中方案，既考慮到平穩範圍的大小，又顧及到有效資料的數量。

3.3 本徵假設

  本徵假設（Intrinsic Hypothesis）又稱內蘊假設，其與變異函數有關。這一假設認為，區域化變數的增量滿足以下兩個條件：在整個研究區域內，區域化變數增量的數學期望為0；且其方差函數存在，並只依賴於滯後距，而與所處位置無關。

  將上述兩個條件用公式分別表達為：

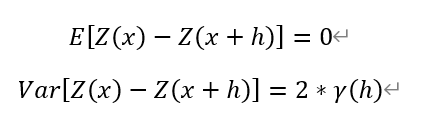
  當E(x)存在時，上述第一個公式可以寫作：

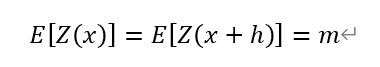
  其中，Var[Z(x)-Z(x+h)]為區域化變數Z(x)與Z(x+h)所對應的方差函數，γ(h)為區域化變數在滯後距為h時的變異函數，m為一常數，h為滯後距，其它符號同前述意義。

  同樣的，上述本徵假設亦是針對整個研究區域範圍而言。若區域化變數僅僅在整個研究區域內的某個有限區域中滿足上述條件，則稱此區域化變數滿足準本徵假設（Quasi Intrinsic Hypothesis）。與準二階平穩性假設類似，準本徵假設亦可視作一種折中方案，其同樣既考慮到了本徵假設對應範圍的大小，又顧及到了有效資料的數量。

  此外，本徵假設是地統計學中對隨機函數的基本假設。

3.4 不同假設對比

  結合上述二階平穩性假設與本徵假設相關原理，可以看到兩種假設的討論物件具有一定區別：二階平穩性假設更多是討論某一特定研究區域內區域化變數自身【即Z(x)】的特徵，而本徵假設則是研究區域化變數所對應增量【即Z(x)-Z(x+h)】的特徵。

  一般認為，二階平穩性假設對區域化變數的要求較之本徵假設更為嚴格，即若某個研究區域內的某一區域化變數滿足二階平穩性假設，則其一定滿足本徵假設；反之則反，若僅知區域化變數滿足本徵假設，則其不一定滿足二階平穩性假設。

  再結合平穩假設，上述三種假設的嚴格程度由大至小依次排列為：平穩假設、二階平穩性假設與本徵假設。

  此外，結合二階平穩性假設的兩個條件，還可以推出協方差函數與變異函數之間的關係：

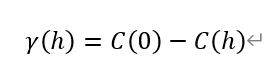
  其中，γ(h)為區域化變數所對應變異函數，C(0)為距離為0時此區域化變數所對應的協方差取值【即基臺值γ(∞)】，C(h)為距離為h時此區域化變數所對應的協方差取值。

  由這一關係可知，用以衡量某一區域化變數在相距為h的兩空間位置點分別取值的自相關性的指標——協方差函數與變異函數之間具有相互關係。因此，在滿足二階平穩性假設的條件下，若協方差函數平穩，則可知變異函數平穩，即其取值只與滯後距h有關。

4 變異函數

  克里格插值法需要藉助空間資料的試驗變異函數及其散點圖特點，因此變異函數的計算在克里格插值過程中發揮著重要作用；變異函數及其模型擬合對克里格插值結果精度具有較大影響。

  變異函數（Variogram），又稱為半變異函數、半方差函數（Semi-variogram）等，其用以描述區域化變數的空間變化特徵與強度，被定義為區域化變數增量平方的數學期望。

  在一維條件下，直接將區域化變數Z在位置(x)與(x+h)處的取值Z(x)與Z(x+h)之差的方差定義為變異函數，其因變數為距離h；而在二維或三維條件下，可以將上述一維中具有單一方向的距離h進一步引申為在任意方向α上的距離|h|。具體公式表達為如下。

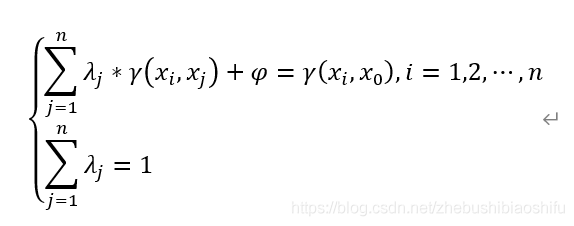
  其中，γ(x,h)即為變異函數。由於公式中在其前具有一個係數2，因此其亦被稱作半變異函數。結合（準）二階平穩性假設、（準）本徵假設等地學基本假設，變異函數取值與區域化變數樣點所處位置x無關，僅僅與樣點之間的距離h有關，則變異函數可以寫作：

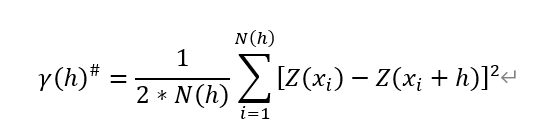
  其中，〖γ(h)〗^#為區域化變數Z(x)的變異函數，N(h)為區域化變數樣點集中距離為h的點對數量，x_i為距離為h時所對應的第i個點。在這裡，距離h亦被稱作滯後距（Lag Distance）。

  一般地，區域化變數變異函數影象往往呈現出「先快速上升，再增速減緩，後趨於平穩」的曲線特徵。其具有三個十分重要的相關概念，分別為塊金常數（Nugget）、基臺值（Sill）與變程（Range）。

  塊金常數代表區域化變數的隨機性大小。由理論角度，在間距為0（即滯後距為零）時，區域化變數取樣點數值應當相等；而在間距無限趨近於0時，對應變異函數數值應當亦向0趨近。但是，在實際研究中，試驗變異函數在滯後距為0時，其取值並不為0，而是一個大於0的數值。這一數值便稱為塊金常數。一般地，上述塊金效應的產生可以歸因於測量誤差，或小於取樣間隔距離處的空間變化。

  基臺值用以衡量區域化變數變化幅度的大小。當滯後距無限增大併到達某一程度後，試驗變異函數若趨於平穩，則這一平穩水平所對應的數值即為基臺值。然而，並不是所有的區域化變數均具有基臺值——如無基臺值模型對應的變異函數。

  變程用以衡量區域化變數自相關範圍的大小。當滯後距無限增大併到達某一程度後，試驗變異函數若趨於平穩，則此時對應的滯後距即為變程。其中，小於變程的距離所對應的樣本位置與空間自相關，而大於變程的距離所對應樣本位置不存在空間自相關。

  此外，變異函數還有其它相關指標，如基臺值與塊金常數的差值——偏基臺值（Partial Sill），用以衡量空間變異性程度的塊金常數與基臺值的比值——塊金係數等。

  基於不同區域化變數對應的變異函數特徵，可以將其分為不同類別。依據變異函數基臺值的有無，可以將模型分為有基臺值模型、無基臺值模型與孔穴效應模型。

  其中，有基臺值模型可以依據變異函數的特徵進一步分為純塊金效應模型（Pure Nugget Effect Model）、球狀模型（Spherical Model）、指數模型（Exponential Model）、高斯模型（Cubic Model或Gaussian Model）與線性有基臺模型（Linear with Sill Model）等。上述幾種模型中，較為常用的模型包括球狀模型、指數模型與高斯模型。

  此外，同樣依據變異函數的特徵，無基臺值模型還可進一步分為線性無基臺值模型、冪指數模型與對數模型等。同樣的，孔穴效應模型可分為基臺值模型和無基臺值模型。

  同時，針對某種區域化變數而言，其在不同方向、不同滯後距情況下可能受到不同因素影響；套合結構可以很好解決這一問題。套合結構可以表示為多個變異函數之和，每一個變異函數均代表著某種方向或某一尺度中的變異性，從而對區域化變數的特徵加以更好概括。

5 克里格插值

  克里格插值法（Kriging Method）又稱為空間區域性插值法，是以上述變異函數理論及其結構分析為基礎，在有限區域內對區域化變數進行線性無偏最優估計（Best Linear Unbiased Prediction，BLUP）的一種方法，在地統計學中也被稱為空間最優無偏估計器（Spatial BLUP）。其中，上述「線性」是指克里格插值法對未知點屬性數值的估計採用線性估計，其公式如下：

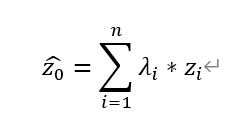
  其中，(z_0 ) ̂是區域化變數在點(x_0,y_0 )位置處的預測值，λ_i為第i個已知點的權重係數，z_i為第i個已知點的實測值。

  上述權重λ_i可以使得各點處的預測值與實測值之間的方差最小，而求取這一權重則為克里格插值的主要內容。

  上述「無偏」是指區域化變數在各點上估計量的數學期望等於其在同一位置上的真實值，公式如下：

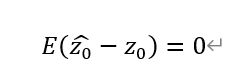
  結合本徵假設，無偏性可以表示為：

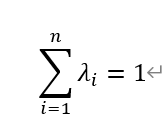
  上述「最優」是指區域化變數在各點上估計量與其在同一位置上的真實值的方差最小，公式如下：

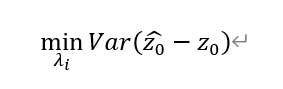
  其中，上述方差被稱作估計方差或估值方差，是對估值準確程度的一種定量表示；而在克里格插值方法中，又可以稱為克里金方差。後續將克里金方差記作σ_k^2。

  經過統計學相關推導，可以將克里金方差寫作：

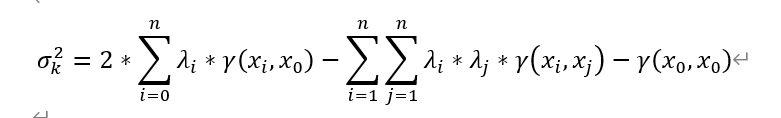
  由此轉換為在無偏條件約束下的最小值求解問題。引入拉格朗日乘子φ，構造拉格朗日函數：

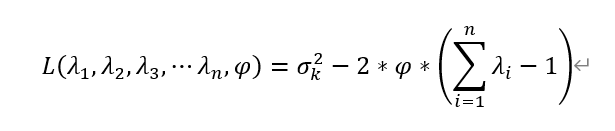
  對權值與拉格朗日乘子求一階偏微分：

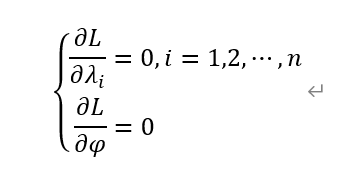
  偏微分求解結果為：

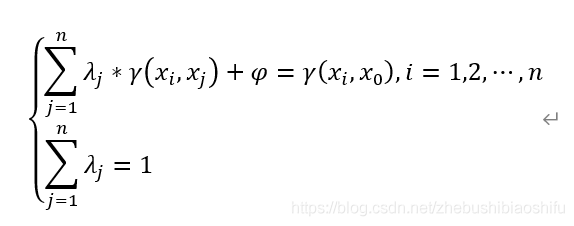
  將上述求和部分展開：

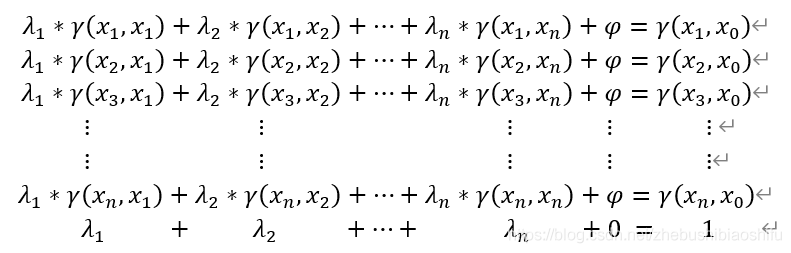
  可將上式進一步寫為矩陣相乘形式，即化為：

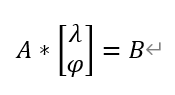
  其中，A代表在原有變異函數矩陣中額外新增全1行與全1列（交界處1換為0）後的矩陣，λ代表各權重組成的列向量，φ代表前述分析引入的拉格朗日乘子，B為各位置與待求解位置對應距離的變異函數值組成的列向量，且在列尾增加一個1。

  由此，即將上述函數轉化為(n+1)個未知數、(n+1)個表示式組成的方程組；通過矩陣求逆，求解方程組即可得到待求解位置與其它已知點的權重。對每一個待插點進行同樣操作，完成克里格插值。

6 迴歸克里格

  正如上述分析，普通克里格（Ordinary Kriging）方法更多依靠所選取樣點資料對空間加以插值，其插值效果較依賴於取樣點的個數、密度，以及其資料的準確性；另一方面，許多空間屬性往往受到其它環境變數的影響。例如，土壤有機碳含量與氣溫、海拔、降水量、坡度等多種環境因子在0.05水平顯著相關；近地面氣溫與海拔、海陸距離、NDVI等環境因子在0.01水平顯著相關。由此觀之，若簡單地忽略環境要素對待插值空間屬性的影響，可能會降低最終插值結果精度。

  基於這種考慮，可以使用迴歸克里格（Regression Kriging）方法對環境因素加以考慮。應用迴歸克里格插值，首先需要確定目標變數與輔助環境變數之間的相關性；確認相關關係符合要求後，建立目標變數與環境變數的一元或多元迴歸模型，從而剔除空間趨勢項。隨後，依據取樣點實測資料與迴歸模型計算得出的對應位置數值，求得目標變數的確定性趨勢項。運用普通克里格方法，將殘差進行插值，並最終將回歸預測的趨勢項與普通克里格的插值結果相加，從而得到目標變數估測值。

  最終空間插值結果的公式表達為：

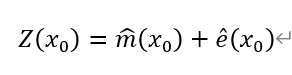
  其中，Z(x_0 )為迴歸克里格估值在x_0位置的結果，m ̂(x_0 )為確定性趨勢項在這一位置的取值，e ̂(x_0 )為殘差普通克里格插值在這一位置的取值。對研究區域內每一位置執行同樣操作，完成迴歸克里格插值。

  一般地，對於所受外界影響較大的空間屬性，迴歸克里格插值效果優於普通克里格插值。

  另一方面，如前所述，儘管迴歸克里格方法對於殘差項的估計仍採用普通克里格插值計算，但由於其對最終目標變數插值結果的影響較之由環境因子得到的空間確定性趨勢項而言仍較低，因此迴歸克里格方法所得結果較之普通克里格方法結果將會粗糙、破碎一些。此外，由方法考慮的因素這一角度來看，迴歸克里格方法與協同克里格（Cokriging）方法具有一定相同之處，即二者均利用相關環境因子對目標變數的空間分佈加以估測；而其不同之處在於，迴歸克里格的輔助資料為面狀分佈，如柵格圖層；而協同克里格的輔助資料為點狀分佈。但無論採取何種方法，最終所得插值結果均為一個完整的表面。