深度學習入門系列之doc

這周老師讓把深度學習的名詞過一遍，小瑪同學準備在過一遍Deep Learning名詞的同時把基本的模型也過一遍。
感謝傑哥發我深度學習入門系列能讓我有機會快速入門。
下面就來doc一些學到的東西

線性感知器

感知器（線性單元）有個問題就是當面對的資料集不是線性可分的時候，「感知器規則」可能無法收斂，這意味著我們永遠無法完成一個感知器的訓練。（即如果我們需要用感知器（神經元）擬合的對映不是線性的，那麼需要用在擬閤中新增非線性的函數）

SGD vs BGD

SGD: Stochastic Gradient Descent
BGD: Batch Gradient Descent
SGD 和 BGD 之間的主要區別在於每次迭代的更新步驟。BGD 在每一步都使用整個資料集計算梯度，而 SGD 在每一步都使用單個樣本或一小批樣本計算梯度。這使得 SGD 比 BGD 更快，計算成本更低。
然而，在凸集中，由於其隨機性質，SGD 可能永遠無法達到全域性最小值，而是不斷在接近全域性最小值的區域內遊蕩。另一方面，BGD 只要有足夠的時間和合適的學習率，就能保證找到全域性最小值。
但是在非凸集中，隨機性有助於我們逃離一些糟糕的區域性最小值。

感知器 vs 神經元

一般情況下，說感知器的時候，它的啟用函數是階躍函數；當我們說神經元的時候，啟用函數往往選擇為sigmoid函數或者是tanh函數。

sigmoid函數

sigmoid函數的導數非常有趣，它可以用sigmoid函數自身來表示。這樣，一旦計算出sigmoid函數的值，計算它的導數的值就非常方便。
令 \(y = sigmoid(x)\) , 則 \(y^{\prime} = y(1 − y)\)

梯度檢查

下面是梯度檢查的程式碼。如果我們想檢查引數的梯度是否正確，我們需要以下幾個步驟：

首先使用一個樣本 \(d\) 對神經網路進行訓練，這樣就能獲得每個權重的梯度。
將 \(w_{ji}\) 加上一個很小的值( \(10^{-4}\) )，重新計算神經網路在這個樣本 \(d\) 下的 \(E_{d+}\)。
將 \(w_{ji}\) 減上一個很小的值( \(10^{-4}\) )，重新計算神經網路在這個樣本 \(d\) 下的 \(E_{d-}\) 。
根據下面的公式計算出期望的梯度值，和第一步獲得的梯度值進行比較，它們應該幾乎想等(至少4位元有效數位相同)。

\[\frac{\partial E_d(w_{ji})}{\partial w_{ji}} \approx \frac{f(w_{ji} + \epsilon) - f(w_{ji} - \epsilon)}{2\epsilon} \]

當然，我們可以重複上面的過程，對每個權重 \(w_{ji}\) 都進行檢查。也可以使用多個樣本重複檢查。

折積神經網路

CNN 更適合影象，語音識別任務，它兒孫輩的人才包括谷歌的GoogleNet、微軟的ResNet。

梯度消失問題

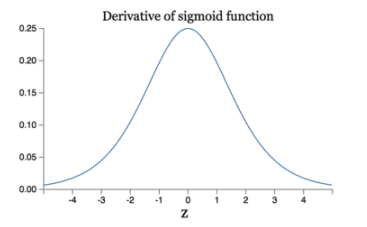
減輕梯度消失問題回憶一下計算梯度的公式 \(\nabla = \sigma^{\prime}\delta x\) 。其中，\(\sigma^{\prime}\) 是sigmoid函數的導數。在使用反向傳播演演算法進行梯度計算時，每經過一層
sigmoid神經元，梯度就要乘上一個 \(\sigma^{\prime}\) 。從下圖可以看出，\(\sigma^{\prime}\) 函數最大值是1/4。因此，乘一個 \(\sigma^{\prime}\) 會導致梯度越來越小，這對於深層網路的訓練是個很大的問題。

ReLU 函數的優勢

Relu函數作為啟用函數，有下面幾大優勢：

速度快和sigmoid函數需要計算指數和倒數相比，relu函數其實就是一個max(0,x)，計算代價小很多。
減輕梯度消失問題而relu函數的導數是1，不會導致梯度變小。當然，啟用函數僅僅是導致梯度減小的一個因素，但無論如何在這方面relu的表現強於sigmoid。使用relu啟用函數可以讓你訓練更深的網路。
稀疏性通過對大腦的研究發現，大腦在工作的時候只有大約5%的神經元是啟用的，而採用sigmoid啟用函數的人工神經網路，其啟用率大約是50%。有論文聲稱人工神經網路在15%-30%的啟用率時是比較理想的。因為relu函數在輸入小於0時是完全不啟用的，因此可以獲得一個更低的啟用率。