論文資訊

論文標題：Pairwise Adversarial Training for Unsupervised Class-imbalanced Domain Adaptation
論文作者：Weili Shi, Ronghang Zhu, Sheng Li
論文來源：KDD 2022
論文地址：download
論文程式碼：download
視屏講解：click

1 摘要

　　提出問題：類不平衡問題；

　　解決方法：

- 提出了一種新穎的成對對抗訓練方法，該方法從源域和目標域的成對樣本中生成對抗樣本，並進一步利用這些樣本來增強訓練資料；
- 提出了一種新的優化演演算法來解決成對對抗訓練問題；

2 問題定義

　　In class-imbalanced domain adaptation, both the source and target domains suffer from label distribution shift. We are given a source domain $\mathcal{D}_{s}=\left\{\left(x_{i}^{s}, y_{i}^{s}\right)\right\}_{i=1}^{N_{s}}$ with $N^{s}$ labelled samples and a target domain $\mathcal{D}_{t}=\left\{x_{i}^{t}\right\}_{i=1}^{N_{t}}$ with $N^{t}$ unlabelled samples. Each domain contains $K$ classes, and the class label is denoted as $y^{S} \in\{1,2, \ldots, K\}$ . Let $p$ and $q$ denote the probability distributions of the source and target domains, respectively. We assume that both the covariate shift (i.e., $p(x) \neq q(x)$ ) and label distribution shift (i.e., $p(y) \neq q(y)$ and $p(x \mid y) \neq q(x \mid y)$) exist in two domains. The model typically consists of a feature extractor $g: \mathcal{X} \rightarrow \mathcal{Z}$ and a classifier $f: \mathcal{Z} \rightarrow \boldsymbol{y}$ . The predicted label $\hat{y}=f(g(x))$ and empirical risk is defined as $\epsilon=\operatorname{Pr}_{x \sim \mathcal{D}}(\hat{y} \neq y)$ , where $y$ is ground-truth label. The source error and target error are denoted as $\epsilon_{S}$ and $\epsilon_{T}$ , respectively. Our goal is to train a model that can reduce gap between source and target domains and minimize $\epsilon_{S}$ and $\epsilon_{T}$ under label distribution shift.

3 方法

3.1 標籤偏移

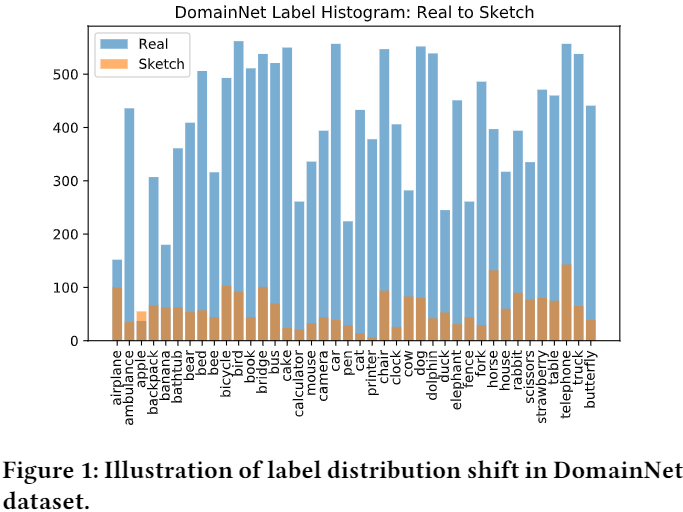
　　Note：簡單增加兩個域的資料來解決標籤偏移是微不足道的，因為還要考慮域偏移的影響，本文通過生成對抗樣本來緩解源域和目標域中的不平衡問題；

3.2 整體框架

　　整體框架：

　　使用對抗訓練增強模型魯棒性，對抗損失如下：

　　　　$\begin{array}{l}\mathcal{L}_{c e}\left(x+\delta^{*}, y ; \theta\right) \\where \quad \delta^{*}:=\arg \max \mathcal{L}_{c e}(x+\delta, y ; \theta) , \|\delta\|_{p} \leq \epsilon \end{array} \quad\quad\quad(1)$

　　傳統對抗訓練在 CDA 中不適用的原因：

- 大多僅從原始樣本的鄰域生成對抗樣本，沒有考慮源域和目標域之間的域差距；
- 無法處理類不平衡問題；

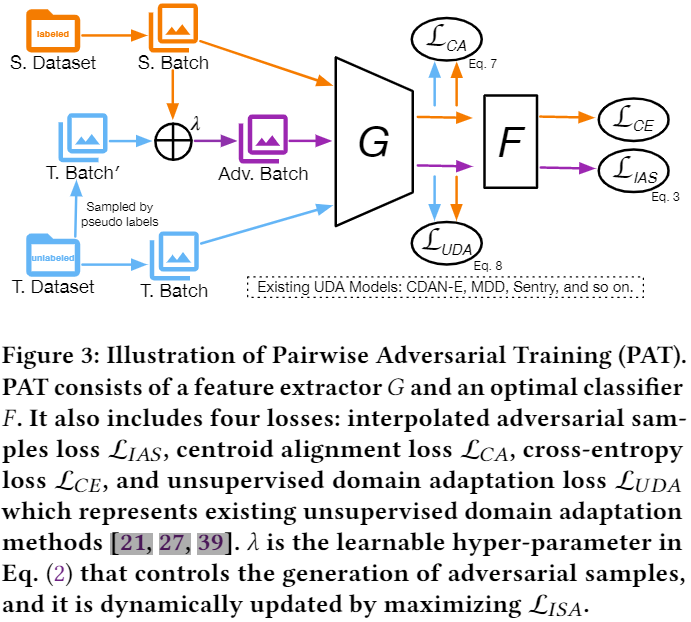
　　基於上述兩個原因，本文提出從源和目標域使用動態線性差值動態生成對抗樣本來緩解類不平衡問題，以及通過顯式對齊源域和目標域的條件特徵分佈來減少域差異，如 Figure 3 所示：

3.3 內插對抗樣本生成

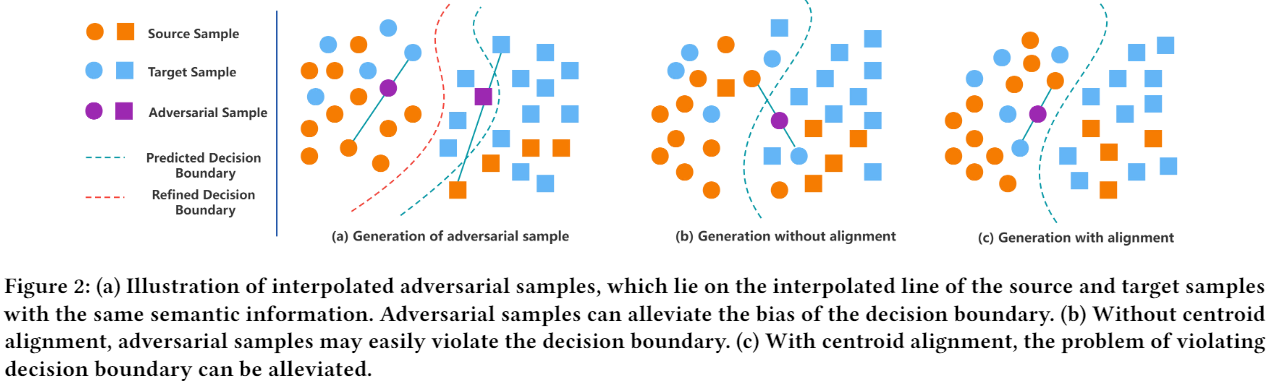
　　如 Figure2(a) 所示，對來自同一類的成對源和目標樣本進行線性插值來生成對抗樣本，插值對抗樣本 (IAS) 應與其對應的源樣本和目標樣本具有相同的語意。通過動態利用內插對抗樣本明確解決了源域中的資料不平衡問題，提高了無偏模型的泛化能力，並且可以隱式地解決目標域中的資料不平衡問題。

　　對於第 $k$ 類，插值的對抗樣本可以定義為：

　　　　$X_{k}^{a d v}=\left\{x_{i}^{a d v} \mid x_{i}^{a d v}=x_{i}^{s}+\lambda\left(x_{i}^{t}-x_{i}^{s}\right), \lambda \in[0,1)^{C}, y_{i}^{s}=\hat{y}_{i}^{t}=k\right\} \quad\quad\quad(2)$

　　其中：

　　　　$\hat{y}_{i}^{t}$ 是通過分類器生成的偽標籤；

　　儘管採用偽標籤來生成對抗樣本，但 PAT 對潛在的錯誤累積問題具有魯棒性，原因：

- 錯誤分類的目標樣本通常存在於決策邊界，儘管目標樣本的偽標籤實際上並不正確，但由於新樣本可能更接近源樣本，因此生成的對抗樣本很有可能仍然與相應的源樣本保持相同的語意資訊；
- 生成的對抗樣本是動態產生的，隨著模型逐漸收斂，不良對抗樣本的不利影響可能減小；

　　Note：本文中並非所有類都有相同的機會生成對抗樣本，採用概率閾值 $P_{k}$ 來控制來自第 $k$ 類的一對源樣本和目標樣本的對抗樣本的生成。

　　插值對抗樣本的生成可以通過解決以下優化問題來實現：

　　　　$\begin{array}{l}\mathcal{L}_{I A S}:=\mathcal{L}_{C E}\left(\hat{x}^{a d v}, y ; \theta\right) \\\text { where } \quad \hat{x}^{a d v}=\underset{x^{a d v} \in \mathcal{X}^{a d v}}{\arg \max } \mathcal{L}_{C E}^{\prime}\left(x^{a d v}, y ; \theta\right)\end{array} \quad\quad\quad(3) $

　　外部最小化使用標準交叉熵損失 $\mathcal{L}_{C E}$，即：

　　　　$\mathcal{L}_{C E}\left(\hat{x}^{a d v}, y ; \theta\right)=-\log \left(\sigma_{y}\left(f\left(g\left(\hat{x}^{a d v}\right)\right)\right)\right) \quad\quad\quad(4)$

　　內部最大化使用交叉熵的修改版，可以緩解熵損失最大化時梯度爆炸或消失的問題，它寫成：

　　　　$\mathcal{L}_{C E}^{\prime}\left(x^{a d v}, y ; \theta\right)=\log \left(1-\sigma_{y}\left(f\left(g\left(x^{a d v}\right)\right)\right)\right. \quad\quad\quad(5)$

　　本文生成對抗樣本的方法如 Algorithm 1：

　　IAS 程式碼：

def get_perturb_point(self,input_source,labels_source):
    self.model.train(False)
    src_point = []
    tgt_point = []
    point_label = []

    for src_index,label in enumerate(labels_source):  
        if torch.rand(1) > self.thresh_prob_class[label.cpu().item()]:
            cond_one = self.target_label == label
            cond_two = self.target_prob > self.thresh_prob_pesudo
            cond = torch.bitwise_and(cond_one, cond_two)
            cond_index = torch.nonzero(cond,as_tuple=True)[0]
            if cond_index.size(0) > 0:
                src_sample = input_source[src_index]
                tgt_index = cond_index[torch.randint(cond_index.size(0),(1,))]
                _,tgt_sample,_ = self.target_dataset[tgt_index]
                src_point.append(src_sample)
                tgt_point.append(tgt_sample)
                point_label.append(label)

    if len(point_label) <= 1:
        return None

    src_point = torch.stack(src_point)    
    tgt_point = torch.stack(tgt_point) 
    point_label = torch.as_tensor(point_label).long()

    src_point = src_point.to(self.device)
    tgt_point = tgt_point.to(self.device)
    point_label = point_label.to(self.device)

    perturb_num = src_point.size(0)
    cof = torch.rand(perturb_num,3,1,1,device=self.device)
    cof.requires_grad_(True)

    optim = SGD([cof],lr=0.001,momentum=0.9)
    loop = self.max_loop
    for i in range(loop):
        optim.zero_grad()
        perturbed_point = src_point + cof * (tgt_point - src_point)
        _,perturbed_output,_,_ = self.model(perturbed_point) 

        perturbed_output_softmax = 1 - F.softmax(perturbed_output, dim=1)
        perturbed_output_logsoftmax = torch.log(perturbed_output_softmax.clamp(min=self.epsilon))          
        loss = F.nll_loss(perturbed_output_logsoftmax, point_label,reduction='none')
        final_loss = torch.sum(loss)
        final_loss.backward()

        optim.step()
        cof.data.clamp_(0,1)
        self.model.zero_grad()

    cof = cof.detach()
    perturbed_point = src_point + cof * (tgt_point - src_point)
    self.model.train(True)
    return (perturbed_point,point_label)

IAS Code

3.4 類不平衡語意質心對齊

　　本文中並非所有類都有相同的機會生成對抗樣本，採用概率閾值 $P_{k}$

　　　　${\large P_{k}=\frac{n_{k}}{n_{\max }+\tau}} \quad\quad\quad(6)$

　　其中：

　　　　$n_{k}$ 是第 $k$ 類的樣本數；

　　　　$n_{\max }= \max _{k}\left\{n_{k}\right\}_{k=1}^{K}$；

　　此外，使用移動平均質心對齊[38]，顯式匹配兩個域的質心來對齊源域和目標域的條件特徵分佈。

　　如 Figure 2b 所示，如果沒有質心對齊，則可能會從一對樣本中生成對抗性樣本，其中一個樣本與其他類未對齊，從而使對抗性樣本的嵌入超出決策邊界。通過 Figure 2c 所示的質心對齊，可以消除這種越界對抗樣本的出現。移動平均質心對齊的損失函數定義為：

　　　　$\mathcal{L}_{C A}=\sum_{k=1}^{K} \operatorname{dist}\left(C_{k}^{S}, C_{k}^{t}\right) \quad\quad\quad(7)$

　　其中，$C_{k}^{s}$ 和 $C_{k}^{t}$ 分別表示源域和目標域中第 $k$ 類的質心。

3.5 用於類不平衡域自適應的 PAT

　　訓練目標：

　　　　$\mathcal{L}=\mathcal{L}_{U D A}+\mathcal{L}_{C E}+\alpha \mathcal{L}_{I A S}+\beta \mathcal{L}_{C A} \quad\quad\quad(8)$

　　其中：

- interpolated adversarial samples loss $\mathcal{L}_{I A S}$ which aims to dynamically generate adversarial samples to alleviate imbalance issue
- centroid alignment loss $\mathcal{L}_{C A}$ is designed to align the conditional feature distributions of source and target
- standard cross-entropy loss $\mathcal{L}_{C E}$
- unsupervised domain adaptation loss $\mathcal{L}_{U D A}$ which is adopted from existing UDA methods

4 實驗

　　略

5 總結

　　略

遷移學習（PAT）《Pairwise Adversarial Training for Unsupervised Class-imbalanced Domain Adaptation》