【LeetCode動態規劃#10】完全揹包問題實戰,其三(單詞拆分,涉及集合處理字串)
單詞拆分
給定一個非空字串 s 和一個包含非空單詞的列表 wordDict,判定 s 是否可以被空格拆分為一個或多個在字典中出現的單詞。
說明:
拆分時可以重複使用字典中的單詞。
你可以假設字典中沒有重複的單詞。
範例 1:
- 輸入: s = "leetcode", wordDict = ["leet", "code"]
- 輸出: true
- 解釋: 返回 true 因為 "leetcode" 可以被拆分成 "leet code"。
範例 2:
- 輸入: s = "applepenapple", wordDict = ["apple", "pen"]
- 輸出: true
- 解釋: 返回 true 因為 "applepenapple" 可以被拆分成 "apple pen apple"。
- 注意你可以重複使用字典中的單詞。
範例 3:
- 輸入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
- 輸出: false
思路
如果要往揹包問題上靠的話,可以把wordDict中的單詞視為"物品",把字串s的長度視為揹包容量(注意,這裡說的是長度,即s.size)
思路聽上去很常規,但是具體到實現方式上就有點複雜
五步走
1、確定dp陣列含義
如果拿不準dp陣列中的元素是什麼型別,可以看看題目的範例返回的是什麼型別的值,那一般就是需要找的值
這裡題目要判定字典wordDict中的單詞能不能拼成字串s
那麼實現過程中肯定要用字典wordDict中的單詞與當前遍歷區間內擷取到的子串進行比較,要麼相同要麼不同,再結合範例的返回值,可以判斷dp陣列中的值應該是布林型別
回到正題,dp陣列究竟代表什麼意思
假設有一個長度為i的字串s的子串,若dp[i] = true
那麼dp[i]表示該字串可以拆分為1個或多個字典wordDict中的單詞(可以理解為:dp[i]是對遍歷過程中某個子串是否能拆分為wordDict中單詞的一個認證,true就是能拆,false就是拆不了)
2+3、確定遞推公式和初始化dp陣列
這個遞推公式的條件可太多了,為什麼連起來一塊說,看到後面就知道了
首先,因為我們要不斷遍歷字串s並擷取子串,通過查詢子串是否存在於字典wordDict中來判斷當前子串是否可以拆分
為什麼要判斷子串是否可以拆分?
因為一旦遍歷完字串s,那麼此時的子串就是s本身了。進而就可以求s能不能被拆分為字典wordDict中的單詞,這裡體現了dp的思想,即前一輪遍歷的子串會影響下一輪的,最終影響整個結果
所以,第一個條件是:所遍歷區間內的子串必須出現在字典中
在說第二個條件之前,有必要說一下 "不斷遍歷字串s並擷取子串" 的實現方式
其實就是雙指標
for (int i = 1; i <= s.size(); i++) { // 遍歷揹包
for (int j = 0; j < i; j++) { // 遍歷物品
string word = s.substr(j, i - j); //substr(起始位置,擷取的個數)
if (wordSet.find(word) != wordSet.end() && dp[j]) {//這裡wordSet是一個unordered_set
dp[i] = true;
}
}
}
下面用圖來解釋一下遍歷過程
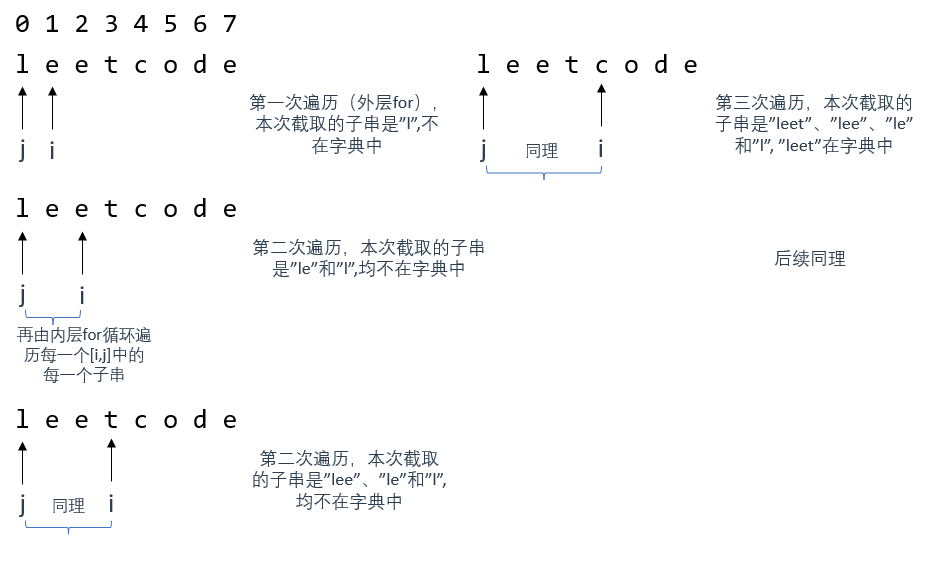
上圖推導了兩層for迴圈的遍歷過程,其中,外層for迴圈負責遍歷字串s(也就是所謂的揹包),而內層for則用來在[j,i]區間內遍歷所有該區域內的子串,用來在wordSet中查詢
如圖所示,當外層for遍歷到 i = 4 ,才獲取到第一個能在wordSet中查詢到的子串"leet"
為什麼不是在i = 3時得到? 因為substr函數擷取子串的區間時左閉右開的,詳見 題外話
注意j遍歷擷取區間[j,i]內所有子串的順序:它是先截最長的(如圖所示)
此時,如果我們將dp[0]初始化為true
那麼,每次i移動的時候,j重置為0,dp[j]就為true
若本次i移動到的位置,在j第一次獲取子串時就能獲取到目標子串的話,其實就找到了一個滿足條件的子串
所以,此時的dp[i]也應該為true
因此,第二個條件就是:[j, i] 這個區間的子串是否出現在字典裡
綜上所述,本題的遞推公式是: if([j, i] 這個區間的子串出現在字典裡 && dp[j]是true) 那麼 dp[i] = true。(j < i )
初始化就是dp[0] = true(我認為完全是為了程式碼實現考慮,沒有別的含義),其餘位置是false
4、確定遍歷順序
因為題目說了,字串s中可能會有"一個或多個"能夠拆分為字典中單詞的子串,也就是說揹包中可以放多個相同的物品(單詞),所以這是一個完全揹包問題
而構成子串必須按一定順序才能構成字串s,所以本題的完全揹包求的是排序(排列有序組合無序)(排列組合的區別詳見)
所以遍歷順序是:先揹包容量後物品
程式碼
太繞了,終於到程式碼了
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
//定義dp陣列
vector<bool> dp(s.size() + 1, false);
//初始化
dp[0] = true;
//遍歷dp陣列
//先將wordDict放入一個unordered_set便於使用子串進行查詢
unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
for(int i = 1; i <= s.size(); ++i){//先遍歷揹包,字串s
for(int j = 0; j < i; ++j){//再遍歷物品
string word = s.substr(j, i - j);//使用j不斷擷取區間內的子串
if(wordSet.find(word) != wordSet.end() && dp[j]) dp[i] = true;
}
}
return dp[s.size()];
}
};