LeetCode 周賽 341 場，模擬 / 樹上差分 / Tarjan 離線 LCA / DFS

本文已收錄到 AndroidFamily，技術和職場問題，請關注公眾號 [彭旭銳] 提問。

大家好，我是小彭。

上週末有單雙週賽，雙週賽我們講過了，單週賽那天早上有事沒參加，後面做了虛擬競賽，然後整個人就不好了。前 3 題非常簡單，但第 4 題有點東西啊，差點就放棄了。最後，被折磨了一個下午和一個大夜總算把第 4 題做出來了，除了新學的 Tarjon 離線演演算法，這道題還涉及到樹上差分、字首和、DFS、圖論等基礎知識，幾度被折磨得想要放棄。這種感覺，似乎和當年在 LeetCode 上做前 10 題的時候差不多哈哈。

加油吧，沒有什麼經驗是隨隨便便能夠獲得的，默默努力，願君共勉。

---

周賽大綱

2643. 一最多的行（Easy）

簡單模擬題，無需解釋。

• 模擬：$O(nm)$

2644. 找出可整除性得分最大的整數（Easy）

簡單模擬題，和 Q1 幾乎相同，這場周賽出的不好。

• 模擬：$O(nm)$

2645. 構造有效字串的最少插入數（Medium）

中等模擬題，不難。

• 模擬：$O(n)$

2646. 最小化旅行的價格總和（Hard）

這道題的考點非常多，難度也非常高。先掌握暴力 DFS 的解法，再分析暴力解法中重複計算的環節，最後推出樹上差分和離線 Tarjan 演演算法。這道題非常非常複雜，

• 遞迴中遞和歸的思想，再理解一下：為什麼你學不會遞迴？談談我的經驗
• 並查集問題，不要錯過：如何使用並查集解決朋友圈問題？
• 差分陣列問題，這個點還沒有寫，同系列的字首和陣列可以參考：使用字首和陣列解決 「區間和查詢」 問題
• 題解 1：暴力 DFS $O(nm)$
• 題解 2：樹上差分 + Tarjan 離線 LCA + DFS $O(n + \alpha m)$

---

2643. 一最多的行（Easy）

題目地址

https://leetcode.cn/problems/row-with-maximum-ones/

題目描述

給你一個大小為 m x n 的二進位制矩陣 mat ，請你找出包含最多 1 的行的下標（從 0 開始）以及這一行中 1 的數目。

如果有多行包含最多的 1 ，只需要選擇 行下標最小 的那一行。

返回一個由行下標和該行中 1 的數量組成的陣列。

題解（模擬）

簡單模擬題。

class Solution {
    fun rowAndMaximumOnes(mat: Array<IntArray>): IntArray {
        var maxIndex = 0
        var maxCount = 0
        for (i in 0 until mat.size) {
            var count = 0
            for (j in 0 until mat[0].size) {
                count += mat[i][j]
            }
            if (count > maxCount) {
                maxCount = count
                maxIndex = i
            }
        }
        return intArrayOf(maxIndex, maxCount)
    }
}

複雜度分析：

• 時間複雜度：$O(nm)$
• 空間複雜度：$O(1)$

---

2644. 找出可整除性得分最大的整數（Easy）

題目地址

https://leetcode.cn/problems/find-the-maximum-divisibility-score/

題目描述

給你兩個下標從 0 開始的整數陣列 nums 和 divisors 。

divisors[i] 的 可整除性得分 等於滿足 nums[j] 能被 divisors[i] 整除的下標 j 的數量。

返回 可整除性得分 最大的整數 divisors[i] 。如果有多個整數具有最大得分，則返回數值最小的一個。

題解（模擬）

簡單模擬題。

class Solution {
    fun maxDivScore(nums: IntArray, divisors: IntArray): Int {
        var maxDivisor = 0
        var maxCount = -1
        for (divisor in divisors) {
            var count = 0
            for (num in nums) {
                if (num % divisor == 0) count++
            }
            if (count > maxCount || count == maxCount && divisor < maxDivisor) {
                maxDivisor = divisor
                maxCount = count
            }
        }
        return maxDivisor
    }
}

複雜度分析：

• 時間複雜度：$O(nm)$
• 空間複雜度：$O(1)$

---

2645. 構造有效字串的最少插入數（Medium）

題目地址

https://leetcode.cn/problems/minimum-additions-to-make-valid-string/

題目描述

給你一個字串 word ，你可以向其中任何位置插入 "a"、"b" 或 "c" 任意次，返回使 word 有效 需要插入的最少字母數。

如果字串可以由 "abc" 串聯多次得到，則認為該字串 有效 。

題解（模擬）

維護當前狀態與目標狀態，當兩個狀態存在偏差時，插入偏差的字元數。

class Solution {
    fun addMinimum(word: String): Int {
        val n = word.length
        var targetStatus = 0
        var index = 0
        var ret = 0
        while (index < n) {
            // 當前狀態
            val curStatus = word[index] - 'a'
            // 插入
            ret += (curStatus + 3 - targetStatus) % 3
            // 目標狀態
            targetStatus = (curStatus + 1) % 3
            index++
        }
        ret += when (targetStatus) {
            0 -> 0
            1 -> 2
            2 -> 1
            else -> 0
        }
        return ret
    }
}

複雜度分析：

• 時間複雜度：$O(n)$
• 空間複雜度：$O(1)$

---

2646. 最小化旅行的價格總和（Hard）

題目地址

https://leetcode.cn/problems/minimize-the-total-price-of-the-trips/

題目描述

現有一棵無向、無根的樹，樹中有 n 個節點，按從 0 到 n - 1 編號。給你一個整數 n 和一個長度為 n - 1 的二維整數陣列 edges ，其中 edges[i] = [ai, bi] 表示樹中節點 ai 和 bi 之間存在一條邊。

每個節點都關聯一個價格。給你一個整數陣列 price ，其中 price[i] 是第 i 個節點的價格。

給定路徑的 價格總和 是該路徑上所有節點的價格之和。

另給你一個二維整數陣列 trips ，其中 trips[i] = [starti, endi] 表示您從節點 starti 開始第 i 次旅行，並通過任何你喜歡的路徑前往節點 endi 。

在執行第一次旅行之前，你可以選擇一些 非相鄰節點 並將價格減半。

返回執行所有旅行的最小价格總和。

問題分析

分析 1：題目的資料結構是樹而不是圖，所以節點之間的最短路是唯一的，不需要使用最短路演演算法。從節點 start 到節點 end 的最優路徑是 start 到最近公共祖先（LCA）+ 最近公共祖先（LCA）到 end；

分析 2：題目可以選擇將一些節點的價格減半，顯然價格越高的節點越應該減半，或者存取次數越多的節點越應該減半。所以我們可以先對每個 trips[i] 跑一次 DFS，並統計每個節點的存取次數 cnts[i]，將每個節點的價格更新為 prices[i] * cnts[i]

分析 3：類似於 337. 打家劫舍 III，如果我們選擇將節點 x 減半（偷竊），那麼與 x 相鄰的節點便不能減半（偷竊）：

• 如果 prices[x] 減半，那麼 x 的最近子節點不能減半；
• 如果 prices[x] 不變，那麼 x 的最近子節點可以減半，也可以不減半，選擇兩種情況的更優解。

題解一（暴力 DFS）

根據問題分析，我們的演演算法是：

• 1、先列舉每種旅途，統計每個節點的存取次數（總共跑 m 次 DFS）；
• 2、更新每個節點的價格權重為 prices[i] * cnts[i]；
• 3、任意選擇一個節點為根節點跑一次 DFS，在每一層遞迴中通過子問題的解得出原問題的解，每個子問題的解有「減半」和「不減半」兩種結果；
• 4、最終，根據根節點的問題求出最終解。

class Solution {
    fun minimumTotalPrice(n: Int, edges: Array<IntArray>, price: IntArray, trips: Array<IntArray>): Int {
        // 建樹
        val graph = Array(n) { LinkedList<Int>() }
        for (edge in edges) {
            graph[edge[0]].add(edge[1])
            graph[edge[1]].add(edge[0])
        }
        // 統計節點存取次數
        val cnts = IntArray(n)
        for (trip in trips) {
            cntDfs(graph, cnts, trip[0], trip[1], -1)
        }
        // 更新價格
        for (i in 0 until n) {
            price[i] *= cnts[i]
        }
        // DFS（打家劫舍）
        val ret = priceDfs(graph, price, 0, -1)
        return Math.min(ret[0], ret[1])
    }

    // return：是否找到目標節點
    private fun cntDfs(graph: Array<LinkedList<Int>>, cnts: IntArray, cur: Int, target: Int, parent: Int): Boolean {
        // 終止條件（目標節點）
        if (cur == target) {
            cnts[cur]++
            return true
        }
        // 列舉子節點（樹的特性：每個方向最多隻會存取一次，不需要使用 visit 陣列）
        for (to in graph[cur]) {
            // 避免迴環
            if (to == parent) continue
            // 未找到
            if (!cntDfs(graph, cnts, to, target, cur)) continue
            // 找到目標路徑，不需要再檢查其他方向
            cnts[cur]++
            return true
        }
        return false
    }

    // return：以 cur 為根節點的子樹的最大價格 <cur 不變, cur 減半>
    private fun priceDfs(graph: Array<LinkedList<Int>>, price: IntArray, cur: Int, parent: Int): IntArray {
        val ret = intArrayOf(
            price[cur],     // x 不變
            price[cur] / 2 // x 減半
        )
        // 列舉子節點（樹的特性：每個方向最多隻會存取一次，不需要使用 visit 陣列）
        for (to in graph[cur]) {
            // 避免迴環
            if (to == parent) continue
            // 子樹結果
            val childRet = priceDfs(graph, price, to, cur)
            ret[0] += Math.min(childRet[0], childRet[1])
            ret[1] += childRet[0]
        }
        return ret
    }
}

複雜度分析：

• 時間複雜度：$O(nm)$ 其中 m 為 trips 陣列的長度，每輪 DFS 的時間是 $O(n)$，計數時間為 $O(nm)$，打家劫舍 DFS 的時間為 $O(n)$；
• 空間複雜度：$O(n + m)$ 樹空間 + DFS 遞迴棧空間，遞迴深度最大為 n。

題解一的瓶頸在於 cntDfs 中的 m 次 DFS 搜尋，如何優化？

預備知識：差分陣列

在 cntDfs 中的每一次 DFS 搜尋中，我們需要將 [start, end] 路徑上的節點存取次數 +1，這正好類似於在陣列上將 [start, end] 區間的位置 + 1，符合 「差分陣列」 的應用場景。我們可以在樹上做差分，再通過一次 DFS 搜尋中計算節點的存取次數。

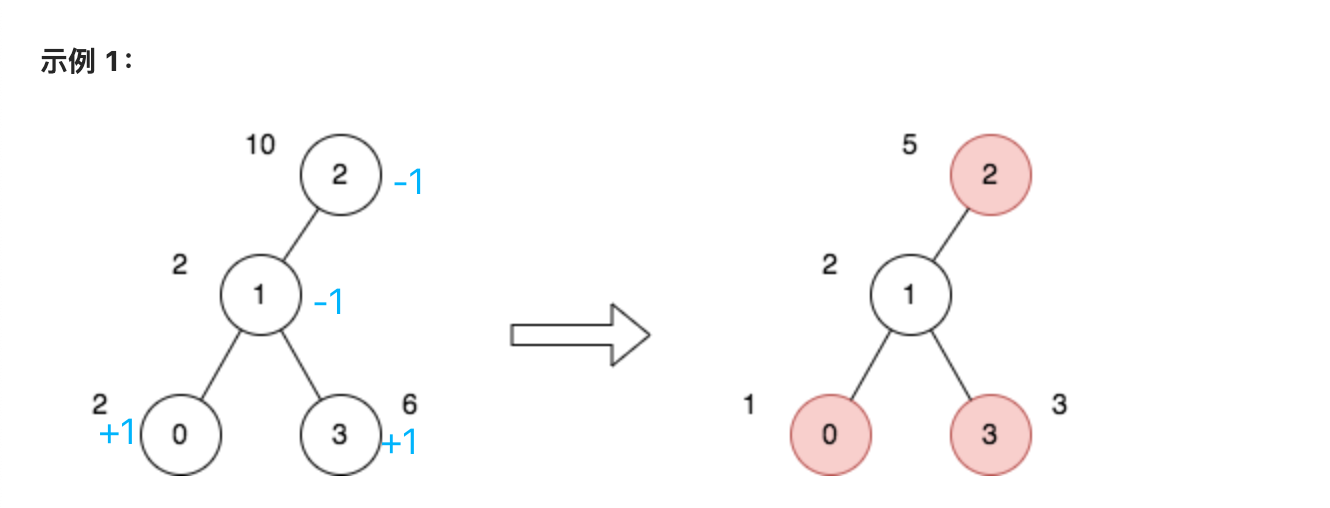
例如在範例 1 中，我們的路徑是 (0, 3)，那麼路徑相當於 [0] + [1,3]，針對這兩條路徑的差分為：

• [0]：diff[0]++，diff[father[0]] —，即 diff[1] —
• [1, 3]：diff[3]++，diff[father[1]] —，即 diff[2]—

那怎麼計算存取次數呢？跟差分陣列一樣，對差分陣列計算字首和就可以獲得節點的存取次數，我們在歸的過程中累加差分值，例如 節點 1 的存取次數就是 +1 + 1 - 1 等於 1 次。

題解二（樹上差分 + Tarjan 離線 LCA + DFS）

考慮到旅行路徑列表是固定的，我們可以使用 Tarjan 離線演演算法，預先求出所有旅行路徑端點的最近公共祖先。反之，如果旅行路徑列表是動態的， 那麼離線演演算法就力不從心了，需要使用複雜度更高的線上演演算法。

參考資料：

• LCA最近公共祖先（Tarjan離線演演算法）
• 圖論 · LCA 最近公共祖先

在題解一中，我們需要花費 m 次 DFS 搜尋來解決 m 個 LCA 問題，Tarjan 演演算法的核心思路是在一次 DFS 搜尋的過程中解決所有 LCA 查詢問題：

• 1、任選一個點為根節點，從根節點開始。
• 2、「遞」的過程（分解子問題）：遍歷該點 u 所有子節點 v，並標記這些子節點 v 已被存取過，若是 v 還有子節點，返回 2 繼續「遞」；
• 3、「歸」的過程：尋找與 u 有查詢關係的點 k。如果 k 節點已經被存取過，那麼 u 和 k 的最近公共祖先就是當前 u 和 k 所在的分組根節點；
• 4、節點 u 的問題結束後，將 節點 u 合併到父節點的集合上。

細節說明：Tarjan 演演算法遞的過程是尋找查詢關係，當路徑的兩個端點都存取過，那麼這兩個端點必然處在同一個分組中，而它們的分組根節點正好就是最近公共元件；

細節說明：為什麼分組根節點正好就是最近公共元件？因為歸是按照 DFS 的搜尋順序迴歸的；

細節說明：如何合併 v 到 u 的集合上？這是並查集的操作，我們定義 parent[x] 表示 x 節點的所處的分組，初始狀態 parent[x] = x；

細節說明：如何查詢與 u 有查詢關係的點 k？預處理準備對映表；

細節說明：為了區分階段狀態，我們定義 color[x] 表示節點 x 的狀態，0 表示未存取、1 表示處於遞迴棧中，2 表示結束。

更多細節，看程式碼吧。

class Solution {
    fun minimumTotalPrice(n: Int, edges: Array<IntArray>, price: IntArray, trips: Array<IntArray>): Int {
        // 建樹
        val graph = Array(n) { LinkedList<Int>() }
        for (edge in edges) {
            graph[edge[0]].add(edge[1])
            graph[edge[1]].add(edge[0])
        }
        // 查詢關係
        val search = Array(n) { LinkedList<Int>() }
        for (trip in trips) {
            search[trip[0]].add(trip[1])
            // 當路徑兩端相同時，避免重複
            if (trip[0] != trip[1]) search[trip[1]].add(trip[0])
        }
        val unionFind = UnionFind(n, graph, search)
        unionFind.tarjan(0, -1/* 無父節點 */)

        // DFS（打家劫舍）
        val ret = priceDfs(graph, price, unionFind.diff, 0, -1)
        return Math.min(ret[0], ret[1])
    }

    // 並查集
    private class UnionFind(val n: Int, val graph: Array<LinkedList<Int>>, val search: Array<LinkedList<Int>>) {
        // 並查集資料結構
        private val parent = IntArray(n) { it }

        // 樹上的父節點
        private val father = IntArray(n)

        // Tarjan 狀態
        private val colors = IntArray(n) //  表示未存取、1 表示處於遞迴棧中，2 表示結束

        // 樹上差分
        val diff = IntArray(n)

        private fun find(x: Int): Int {
            // 路徑壓縮
            if (x != parent[x]) parent[x] = find(parent[x])
            return parent[x]
        }

        // 這道題的合併不能使用按秩合併，必須將子節點 x 合併到 y 的集合中
        private fun merge(x: Int, y: Int) {
            // 按秩合併
            val rootX = find(x)
            val rootY = find(y)
            if (rootX != rootY) parent[rootX] = rootY
        }

        fun tarjan(u: Int, fa: Int) {
            // 記錄父節點
            father[u] = fa
            // 標記已存取
            colors[u] = 1
            // 遞的過程：遍歷 u 的所有子節點 v
            for (v in graph[u]) {
                if (0 != colors[v]) continue // 存取過
                // 繼續遞的過程
                tarjan(v, u)
            }
            // 列舉查詢關係
            for (k in search[u]) {
                if (k == u || colors[k] == 2) {
                    // 找到 u 和 k 的查詢關係，更新樹上差分
                    val lca = find(k)
                    diff[u]++
                    diff[lca]--
                    diff[k]++
                    val lcaParent = father[lca]
                    if (lcaParent >= 0) diff[lcaParent]--
                }
            }
            // 結束
            colors[u] = 2
            if(fa != -1) merge(u, fa) // 將子節點 u 合併到 fa 的集合中
        }
    }

    // return：以 cur 為根節點的子樹的最大價格 <cur 不變, cur 減半>
    private fun priceDfs(graph: Array<LinkedList<Int>>, price: IntArray, diff: IntArray, cur: Int, parent: Int): IntArray {
        val ret = intArrayOf(0, 0, diff[cur])
        // 列舉子節點（樹的特性：每個方向最多隻會存取一次，不需要使用 visit 陣列）
        for (to in graph[cur]) {
            // 避免迴環
            if (to == parent) continue
            // 子樹結果
            val childRet = priceDfs(graph, price, diff, to, cur)
            ret[0] += Math.min(childRet[0], childRet[1])
            ret[1] += childRet[0]
            ret[2] += childRet[2] // 累加字首和
        }
        ret[0] += price[cur] * ret[2]
        ret[1] += price[cur] * ret[2] / 2
        return ret
    }
}

複雜度分析：

• 時間複雜度：$O(n + \alpha m)$ 其中 m 為 trips 陣列的長度，$\alpha$ 是並查集的反阿克曼函數，近似於線性函數；
• 空間複雜度：$O(n + m)$ 樹空間 + DFS 遞迴棧空間，遞迴深度最大為 n。

---