【LeetCode動態規劃#07】01揹包問題一維寫法(狀態壓縮)實戰,其二(目標和、零一和)
目標和(放滿揹包的方法有幾種)
難度:中等
給定一個非負整數陣列,a1, a2, ..., an, 和一個目標數,S。現在你有兩個符號 + 和 -。對於陣列中的任意一個整數,你都可以從 + 或 -中選擇一個符號新增在前面。
返回可以使最終陣列和為目標數 S 的所有新增符號的方法數。
範例:
- 輸入:nums: [1, 1, 1, 1, 1], S: 3
- 輸出:5
解釋:
- -1+1+1+1+1 = 3
- +1-1+1+1+1 = 3
- +1+1-1+1+1 = 3
- +1+1+1-1+1 = 3
- +1+1+1+1-1 = 3
一共有5種方法讓最終目標和為3。
提示:
- 陣列非空,且長度不會超過 20 。
- 初始的陣列的和不會超過 1000 。
- 保證返回的最終結果能被 32 位整數存下。
思路
前者是將集合分成兩個相等的子集,後者是將集合分成兩個儘可能相等的子集
共同點是什麼?都是先把問題轉換成將當前題目給的陣列集合一分為二
因此,本題要往01揹包問題上靠,也要先轉換為一個將集合劃分成兩部分的問題
怎麼轉呢?
題目要在一個非負整數陣列nums中的任意一個整數前加正負號,實現所有元素相加後等於目標值target,最後統計一共有多少種相加的方法(即一共有多少种放正負號的方法)
那麼我們就可以把陣列元素分為兩個子集,一個子集中的元素前面都加正號,另一個子集則都加負號
這不就有兩個子集了嘛(md這正常人能想到?)
設加負號的子集為 negativeSign, 加正號的子集為 plusSign
注意,此時我們討論的兩個子集都是已經通過dp劃分好的,裡面不帶正負號
那麼,兩個子集的元素相加應該等於非負整數陣列nums的元素之和sum
兩個子集的元素相減應該等於目標值target
抽象為公式如下:
① plusSign + negativeSign = sum;
② plusSign - negativeSign = target;
合併一下可以得到: plusSign = (sum + target) / 2;
在01揹包問題中,只需用一個子集充當揹包即可,因此這裡可以選擇 加正號的子集plusSign 作為揹包
以範例 nums: [1, 1, 1, 1, 1], target: 3 來說
轉換為揹包問題後,揹包的容量為 (5+3)/2 = 4 ,所謂的"物品"就是nums陣列中的元素
當然,這裡用除法就會涉及不能整除的情況
若不能整除,代表該陣列nums找不到能夠組合成目標值target的方法,直接return 0
此時,問題就轉換成了:使用非負整數陣列nums中的元素裝滿揹包有幾種方法?
(注意,本題要找的是有幾種裝滿揹包的方法)
區分一下之前做的揹包問題的目標
單純的01揹包問題:裝滿某個揹包時,物品的最大價值;
分割等和子集:往揹包放入物品後,揹包的最大重量(換句話說就是能不能用物品把揹包裝滿,能就return true)
最後一塊石頭:往揹包裝物品,能裝下的最大價值(能裝多少裝多少)
五步走
1、確定dp陣列含義
老規矩,先回顧一下經典01揹包問題的dp陣列定義
dp[j]: 揹包容量為j時,裝滿揹包的最大價值為dp[j]
轉換一下,本題的dp陣列含義可以定義如下:使用所給的所有物品,裝滿容量為j的揹包有dp[j]種方法
2、確定遞推公式
怎麼推匯出dp[j]呢?
這裡要通過"物品"的角度來想,例如,當前如果有一個物品(nums中的一個元素)要放入揹包,假設揹包容量是5(與範例保持一致, nums元素為5個1)
那麼這個物品一定會放入揹包中,因此也一定會佔用掉揹包的一部分容量,佔用掉的容量是 j - nums[i]
根據dp陣列的含義,在有一個物品確定放入的情況下,dp[5]就會轉變為dp[5 - 1],也就是dp[4]
有點亂?那再用直接一點的話描述一下上面發生的事情:
1、最開始,揹包容量是5,此時按dp陣列的定義,裝滿該揹包會有dp[5]種方法;(因為還有五個容量,你隨便怎麼裝,所有的方法就表示為dp[5])
2、當已經有一個"物品"確定放入容量為5的揹包時,揹包容量縮減為4(不管你開始沒開始往裡面放,先給你預留了),還是按定義,此時裝滿該揹包會有dp[5-nums[0]]種方法(即dp[5 - 1] = dp[4])
3、當已經有兩個"物品"確定放入容量為5的揹包時,揹包容量縮減為3(不管你開始沒開始往裡面放,先給你預留了)
按定義,此時裝滿該揹包會有dp[5-nums[0]-nums[1]]種方法(即dp[5-1-1] = dp[3])
後面的情況以此類推
注意,一定要結合dp陣列的定義
這裡的
dp[某某]指的是在"某某"容量下放入物品時,所有方法的集合
簡單概括一下,例如:dp[j],j為5,
- 已經有0個的話,有 dp[5]種方法 湊成 容量為5的揹包。
- 已經有一個1(nums[i]) 的話,有 dp[4]種方法 湊成 容量為5的揹包。
- 已經有一個2(nums[i]) 的話,有 dp[3]種方法 湊成 容量為5的揹包。
- 已經有一個3(nums[i]) 的話,有 dp[2]種方法 湊成 容量為5的揹包
- 已經有一個4(nums[i]) 的話,有 dp[1]種方法 湊成 容量為5的揹包
- 已經有一個5 (nums[i])的話,有 dp[0]種方法 湊成 容量為5的揹包
那湊整dp[5]有多少方法呢?(即dp[5]怎麼求)
就把所有的 dp[j - nums[i]] 累加起來即可
也就是dp[5] = dp[4] + dp[3] + dp[2] + dp[1] + dp[0]
總結為遞推公式就是:
dp[j] += dp[j - nums[i]]
該遞推公式很重要,在用揹包解決排列組合問題時還能用
3、初始化dp陣列
一切結合dp陣列的含義:裝滿容量為j的揹包有dp[j]種方法
來看dp[0]的情況
dp[0]即被包容量為0時裝滿揹包的方法數量,這裡又可以細分為兩種情況:要裝的物品重量不為0和重量為0
如果物品重量不為0
那麼實際上我們是無法將該物品裝入容量為0的揹包中的,那麼是不是就意味著在該種情況下,dp[0] = 0 了呢?
我認為也不是,因為揹包容量為0是一種特殊情況,此時不論你往不往裡面放東西(或者放不放得進),揹包都已經處於放滿狀態,因此
dp[0]應該是預設有一種方式裝滿的,那就是什麼也不放
由上述分析可知,dp[0]應該初始化為1,即dp[0] = 1;
如果物品重量為0
接著上面的分析,若揹包中物品重量為0, 假設:[0,0,0,0,0], target = 0
那這些0就還是可以往揹包裡面放的(放不放都一樣),並且不同的物品(重量為0)往揹包放就算是一種不同的放法
因此,dp[0]就是這五個重量為0的物品不斷組合放入揹包內的組合方式的種類數量
大概有32種,於是dp[0] = 32
以上分析是建立在認同dp[0]應該初始化為1的情況下成立的(因為其他情況都是基於的dp[0] = 1推匯出來的)
說了這麼多,無非就是像說明清楚dp[0]初始化為1的可行性,記住本題 dp[0] = 1 就行
4、確定遍歷順序
仍然遵循先遍歷物品(nums),後遍歷揹包容量的順序,且揹包容量的遍歷方向是倒序的
這裡在邏輯上與之前涉及重量的問題不太一樣,下面手動推導一遍
(輸入:nums: [1, 1, 1, 1, 1], target: 3)
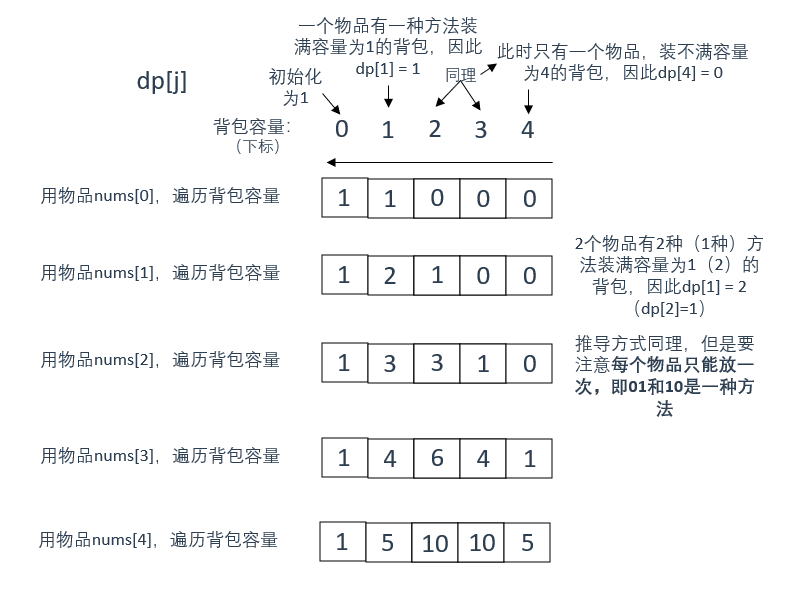
如圖所示為遍歷過程
注意dp陣列的含義,使用所給的所有物品,裝滿容量為j的揹包有dp[j]種方法
這裡有兩個關鍵點:1、需要使用所有的物品;2、裝滿
- 不論遍歷的過程如何,最終我們需要求的是把所有物品放入容量為j的揹包的方法,因為遍歷物品的過程是一個一個遍歷的,所以放入所有物品的方法種類也是由最開始的情況不斷累加到最後才能得到的
- 一定要能夠裝滿當前容量才算是一種方法,比如在容量為4的情況下,目前遍歷到第一個物品(也就是隻有一個物品),無論如何是放不滿4個容量的,因此就算能夠放入當前的一個物品,也不能算一種方法
說一下"裝滿方法"是怎樣計算的
因為01揹包問題中,每個物品只能使用一次,那麼在當前物品能夠裝滿當前容量的前提下,使用相同物品以不同順序放入揹包的方法應該視作同一種方法
什麼意思呢?就是說假設現在遍歷到了nums[2],我們手頭上有3個物品,此時容量遍歷到2的話,理論上我們有以下放入的方式:
nums[0] nums[1] nums[2]
nums[0] nums[2] nums[1]
nums[1] nums[0] nums[2]
nums[1] nums[2] nums[0]
nums[2] nums[1] nums[0]
nums[2] nums[0] nums[1]
其中,有一半的放入方式重複使用了物品,因此是不計入方法種類
程式碼
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
//計算陣列元素之和
int sum = 0;
for(auto num : nums) sum += num;
//判斷兩種無解的情況
//1、所給的target已經大於sum
//2、(sum + target) / 2不能整除,即計算揹包容量時不能整除
if(abs(target) > sum) return 0;//取絕對值
if((sum + target) % 2 != 0) return 0;
//計算揹包容量
int bagSize = (sum + target) / 2;
//定義dp陣列
vector<int> dp(bagSize + 1, 0);
//初始化dp陣列
dp[0] = 1;
//遍歷dp陣列
for(int i = 0; i < nums.size(); ++i){//遍歷物品num
// 如果當前揹包容量小於物品重量,換一個物品繼續遍歷容量(所以第二層迴圈的條件是j >= nums[i])
// 每一個元素一定是不可重複放入,所以從大到小遍歷
for(int j = bagSize; j >= nums[i]; --j){//遍歷揹包容量
dp[j] += dp[j - nums[i]];
}
}
return dp[bagSize];
}
};
零一和
給你一個二進位制字串陣列 strs 和兩個整數 m 和 n 。
請你找出並返回 strs 的最大子集的大小,該子集中 最多 有 m 個 0 和 n 個 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
範例 1:
- 輸入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
- 輸出:4
- 解釋:最多有 5 個 0 和 3 個 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。 其他滿足題意但較小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不滿足題意,因為它含 4 個 1 ,大於 n 的值 3 。
範例 2:
- 輸入:strs = ["10", "0", "1"], m = 1, n = 1
- 輸出:2
- 解釋:最大的子集是 {"0", "1"} ,所以答案是 2 。
提示:
- 1 <= strs.length <= 600
- 1 <= strs[i].length <= 100
- strs[i] 僅由 '0' 和 '1' 組成
- 1 <= m, n <= 100
思路
這題有點繞的其實,剛上手的話很容易將m、n看成兩個容器
其實這樣想是錯誤的,本題實質上還是01揹包問題,只不過這個揹包有"兩個維度"
什麼意思呢?我解釋一下
先來說題意吧,題目要求是:m代表字串中0的個數,n代表字串中1的個數
然後,題目規定一組m、n,要求從字串陣列strs中找到能夠滿足m、n的最大子集,並返回該子集的大小
拿範例1來看,strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
最多有 5 個 0 和 3 個 1 的strs中的最大子集是 {"10(m=1,n=1)","0001(m=3,n=1)","1","0"}
該子集的大小是4,因此結果值返回的是4
看出來了嗎?其實題目規定的"m = 5, n = 3"就是在設定揹包的容量
確定了揹包就好辦了,下面就套五部曲解決問題
五步走
1、確定dp陣列的含義
注意,這裡題目是要求最大子集個數,也就是揹包中物品的個數
那麼dp陣列可以定義如下
dp[i][j]: 在揹包"容量"(這裡的容量指的是strs中一個子字串中0、1的個數)為i、j時能夠裝下物品的最大個數
雖然這裡需要把dp陣列設定成二維的,但其實本質上和之前的一維01揹包問題沒有區別
如果不好理解的話還是可以把dp陣列看成是個一維的,例如dp[G],G是揹包的容量,只不過G由兩個部分組成,一部分是i,一部分是j
(這裡也可以把G想象成strs中一個子字串,例如"10")
2、確定遞推公式
因為本題只是給放入揹包的物品多增加了一個維度,所以遞推公式可以參考標準01揹包問題的遞推公式(一維)
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
那麼對照著本題的遞推公式就是
dp[i][j] = max(dp[i][j], dp[i - zeroNums][j - oneNums] + 1(物品數量));
解釋一下,
當我們確定放入一個新的子字串(假設是"10"),那麼此時揹包容量(i、j)就要對應減少子字串中0的個數(zeroNums)、子字串中1的個數(oneNums),(zeroNums, oneNums)即為該子字串(物品)的重量
當然,此時包內的物品數量要加1(類比之前的遞推公式,揹包總價增加)
推導dp[i][j]時,有兩種情況:放東西和不放東西
這兩者取能夠使物品個數最大的那種情況就行,即上面的遞推公式
3、初始化dp陣列
dp[0][0]時要初始化為0,即容量為(0,0)時,一個也裝不下
然後其餘的部分也要初始化為0,為了防止遞推值被初始值覆蓋(詳見)
4、確定遍歷順序

和普通的01揹包的一維解法一樣,這裡也是先遍歷物品(子字串),然後倒序遍歷揹包容量(i,j)(對應(zeroNums, oneNums))
核心程式碼如下,結合上面的圖來解釋
for (string str : strs) { // 遍歷物品,即子字串,例如"10"
int oneNum = 0, zeroNum = 0;
for (char c : str) {//統計字串中0、1的數量
if (c == '0') zeroNum++;
else oneNum++;
}//以下是遍歷揹包容量(i,j)
//如果當前揹包容量(i,j)小於物品重量(zeroNum,oneNum),換一個物品(子字串)再放入
for (int i = m; i >= zeroNum; i--) { // 遍歷揹包容量且從後向前遍歷!
for (int j = n; j >= oneNum; j--) {
dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
}
}
}
對應到圖中就是,我們第一輪遍歷是從最下面的一行開始的,從右往左倒序遍歷
根據遞推公式有:dp[3][3] = max(dp[3][3], dp[3 - 1][3 - 1] + 1);(此時子字串是"10")
因為dp[3][3]的初始值為0,所以dp[2][2]+1肯定要大一些,故dp[3][3] = dp[3 - 1][3 - 1] + 1;
那dp[2][2]又是多少?還是用遞推公式去算,得到dp[2][2] = max(dp[2][2], dp[2 - 1][2 - 1] + 1);,取決於dp[1][1]
同理,dp[1][1] = max(dp[1][1], dp[1 - 1][1 - 1] + 1);,最後可以算出dp[1][1]=dp[0][0]+1=1
所以,
dp[2][2]=1+1=2
dp[3][3]=2+1=3
此時可以得到圖中dp[3][3]處的遞推值,同理可以把整個dp陣列的遞推值計算出來,結果如上圖所示
程式碼
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
//定義dp陣列,並初始化
//二維陣列,行列分別是0、1(可以顛倒)
vector<vector<int>> dp(m + 1, vector(n + 1, 0));
//遍歷dp陣列
for(string str : strs){//遍歷物品(子字串)
int zeroNums = 0, oneNums = 0;
//統計字串中的01個數
for(char c : str){
if(c == '0'){
zeroNums++;
}else oneNums++;
}
for(int i = m; i >= zeroNums; --i){//遍歷揹包容量(i,j),倒序
for(int j = n; j >= oneNums; --j){//i\j遍歷順序可以更換,因為本質上還是容量
dp[i][j] = max(dp[i][j], dp[i - zeroNums][j - oneNums] + 1);
}
}
}
return dp[m][n];
}
};