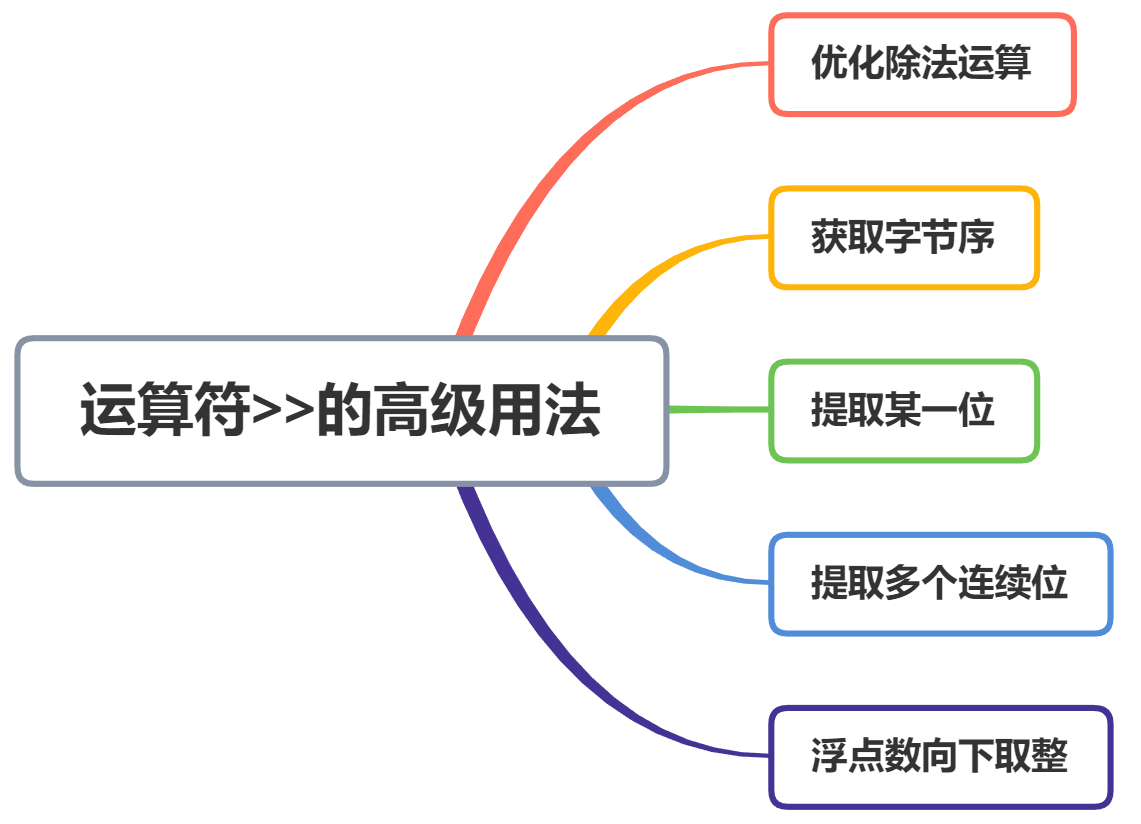
逍遙自在學C語言 | 位運運算元>>的高階用法

2023-04-17 06:00:48

前言

在上一篇文章中，我們介紹了<<運運算元的高階用法，本篇文章，我們將介紹>> 運運算元的一些高階用法。

一、人物簡介

第一位閃亮登場，有請今後會一直教我們C語言的老師 —— 自在。

第二位上場的是和我們一起學習的小白程式猿 —— 逍遙。

二、優化除法運算

除法運算需要比位移運算需要更多的計算資源，某些情況下采用位移運算可以提高效能
程式碼範例

#include <stdio.h>
int main()
{
    int a = 1024;
    int b = a / 8; // 整除8
    int c = a >> 3; // 相當於除以8
    printf("b = %d, c = %d\n", b, c);
    return 0;
}

每右移一位相當於除以2， a >> 3相當於a/(2*2*2) = a/8；
執行結果

三、獲取位元組序

大端模式：是指資料的高位元組儲存在記憶體的低地址中，而資料的低位元組儲存在記憶體的高地址中。
小端模式：是指資料的高位元組儲存在記憶體的高地址中，而資料的低位元組儲存在記憶體的低地址中。
右移運運算元還可以用於獲取當前系統的位元組序（即大端序或小端序）
比如數位 0x1234在記憶體中的表示形式為：

大端模式：
低地址 -----------------> 高地址
0x12 | 0x34

小端模式：
低地址 ------------------> 高地址
0x34 | 0x12
程式碼範例

#include <stdio.h>
int main()
{
    short int i = 0x1234; // 假設i在記憶體中的地址為0x1000
    char *p = (char *)&i; // 將i的地址轉換為字元型指標，即指向0x1000的位元組型指標
    if (*p == 0x12) // 判斷*p的值是否等於0x12，如果等於則為大端序，否則為小端序
    {
        printf("大端序\n");
    }
    else
    {
        printf("小端序\n");
    }
    return 0;
}

執行結果

四、提取二進位制數的某一位

將一個二進位制數右移n位，再與1進行按位元與運算，得到的結果就是這個二進位制數的第n位(從第0位開始算)
例如，將1011右移2位，得到的結果是10，再與1進行按位元與運算，得到的結果是0，即1011的第二位是0
程式碼範例

#include <stdio.h>
int main()
{
    int a = 0b1011;
    int b = (a >> 2) & 1; // 提取a的第二位，即0
    printf("第二位的值為 %d\n", b);
    return 0;
}

執行結果

五、提取二進位制數的多個連續位

將一個二進位制數右移n位，再與一個掩碼進行按位元與運算，得到的結果就是這個二進位制數從第n位開始的若干位
例如，將1011011右移3位，得到的結果是1011，再與111進行按位元與運算，得到的結果是011，即1011011從第3位開始的三位是011
程式碼範例

#include <stdio.h>
int main()
{
    int a = 0b1011011;
    int b = (a >> 3) & 0b111; // 提取a從第3位開始的3位，即101
    printf("b = %d\n", b);
    return 0;
}

執行結果，3 (二進位制為0b011)

六、浮點數向下舍入為整數

這種用法通常用於嵌入式系統中，因為某些嵌入式處理器沒有浮點數運算單元，只能使用整數運算單元來處理浮點數
將一個浮點數乘以一個定點數的精度，並將結果向下取整，可以得到一個整數近似值
例如，將一個浮點數乘以1000，再將結果右移10位，得到的結果就是這個浮點數乘以1000並向下取整的整數值
程式碼範例

#include <stdio.h>
int main()
{
    float x = 3.1415926;
    int a = (int)(x * 1000.0f) >> 10; // 將x乘以1000並向下取整
    printf("向下取整後的數值為 %d\n", a);
    return 0;
}

執行結果

小結

通過這篇文章，我們學會了用位運運算元>>的5種高階用法

1、優化除法運算

2、獲取位元組序

3、提取二進位制數的某一位

4、提取二進位制數的多個連續位

5、浮點數向下舍入為整數