基本資料結構：

一.線性表

1.順序結構

　線性表可以用普通的一維陣列儲存。

　你可以讓線性表可以完成以下操作（程式碼實現很簡單，這裡不再贅述）：

返回元素個數。
判斷線性表是否為空。
得到位置為p的元素。
查詢某個元素。
插入、刪除某個元素：務必謹慎使用，因為它們涉及大量元素的移動。

2.鏈式結構

(1) 單連結串列：

1.定義：下面有一個空連結串列，表頭叫head，並且表內沒有任何元素。

struct node
{
    int value;
    node *next;
} arr[MAX];
int top=-1;
node *head = NULL;

2.記憶體分配：在競賽中不要用new，也不要用malloc、calloc——像下面一樣做吧。

#define NEW(p)        p=&arr[++top];p->value=0;p->next=NULL
node *p;
NEW(head);                            // 初始化表頭
NEW(p);                                // 新建結點

3.插入：把q插入到p的後面。時間複雜度O(1)。

if (p!=NULL && q!=NULL)                // 先判定是否為空指標。如果不是，繼續。
{
    q->next=p->next;
    p->next=q;
}

4.刪除：把p的下一元素刪除。時間複雜度O(1)。

if (p!=NULL && p->next!=NULL)        // 先判定是否為空指標。如果不是，繼續。
{
    node *q=p->next;
    p->next=q->next;
    // delete(q);                        // 如果使用動態記憶體分配，最好將它的空間釋放。
}

5.查詢或遍歷：時間複雜度O(n)。

node *p=first;
while (p!=NULL)
{
    // 處理value
    // cout<<p->value<<'\t';
    p=p->next;
}

(2) 靜態連結串列

指標的作用就是儲存地址。如果我們找到了替代品，就可以放棄指標了。

需要把上面的定義改一下：

struct node
{
    int value;
    int next;            // 表示下一元素在arr中的下標
} arr[MAX];

(3) 迴圈連結串列

和單連結串列有一個重大區別：單連結串列最後一個元素的next指向NULL，而回圈連結串列最後一個元素的next指向first。

遍歷時要留心，不要讓程式陷入死迴圈。

一個小技巧：如果維護一個表尾指標last，那麼就可以在O(1)的時間內查詢最後一個元素。同時可以防止遍歷時陷入死迴圈。

(4) 雙連結串列

1.定義：下面有一個空連結串列，表頭叫first。

struct node
{
    int value;
    node *next, *prev;
} arr[MAX];
int top=-1;
node *first = NULL;    // 根據實際需要可以維護一個表尾指標last。

2.記憶體分配：最好不要使用new運運算元或malloc、calloc函數。

#define NEW(p)        p=arr+(++top);p->value=0;p->next=NULL;p->prev=NULL
node *p;
NEW(head);                            // 初始化表頭
NEW(p);                                // 新建結點

3.插入：把q插入到p的後面。時間複雜度O(1)。

if (p==NULL||q==NULL)                 // 先判定是否為空指標。如果不是，繼續。
{
    q->prev=p;
    q->next=p->next;
    q->next->prev=q;
    p->next=q;
}

4.刪除：把p的下一元素刪除。時間複雜度O(1)。

if (p==NULL||p->next==NULL)        // 先判定是否為空指標。如果不是，繼續。
{
    node *q=p->next;
    p->next=q->next;
    q->next->prev=p;
    // delete(q);                        // 如果使用動態記憶體分配，最好將它的空間釋放。
}

5.查詢或遍歷：從兩個方向開始都是可以的。

(5) 將元素插入到有序連結串列中*

void insert(const node *head, node *p)
{
    node *x, *y;
    y=head;
    do
    {
        x=y;
        y=x->next;
    } while ((y!=NULL) && (y->value < p->value);
    x->next=p;
    p->next=y;
}

二.棧

(1) 棧的實現!

操作規則：先進後出，先出後進。

int stack[N], top=0; // top表示棧頂位置。

入棧：inline void push(int a) { stack[top++]=a; }

出棧：inline int pop() { return stack[--top];

棧空的條件：inline bool empty() { return top<0; }　　

　　如果兩個棧有相反的需求，可以用這種方法節省空間：用一個陣列表示兩個棧。分別用top1、top2表示棧頂的位置，令top1從0開始，top2從N-1開始。

(2) DFS和棧

　　遞迴其實也用到了棧。每呼叫一次函數，都相當於入棧（當然這步操作「隱藏在幕後」）。函數呼叫完成，相當於出棧。

　　一般情況下，呼叫棧的空間大小為16MB。也就是說，如果遞迴次數太多，很容易因為棧溢位導致程式崩潰，即「爆棧」。

　　為了防止「爆棧」，可以將遞迴用棧顯式實現。如果可行，也可以改成迭代、遞推等方法。

　　使用棧模擬遞迴時，注意入棧的順序——逆序入棧，後遞迴的要先入棧，先遞迴的要後入棧。

　　下面是非遞迴版本的DFS模板：

stack <int> s;                                // 儲存狀態
void DFS(int v, …)
{
    s.push(v);                                // 初始狀態入棧
    while (!s.empty())
    {
        int x = s.top(); s.pop();        // 獲取狀態
        
        // 處理結點
        if (x達到某種條件)
        {
            // 輸出、解的數量加1、更新目前搜尋到的最優值等
            …
            return;
        }

        // 尋找下一狀態。當然，不是所有的搜尋都要這樣尋找狀態。
        // 注意，這裡尋找狀態的順序要與遞迴版本的順序相反，即逆序入棧。
        for (i=n-1;i>=0;i--)
        {
            s.push(… /*i對應的狀態*/);
        }
    }

    // 無解
    cout<<"No Solution.";
}

三.佇列

(1) 順序佇列

操作規則：先進先出，後進後出。

定義：int queue[N], front=0, rear=0;

front指向佇列首個元素，rear指向佇列尾部元素的右側。

入隊：inline void push(int a) { queue[rear++]=a; }

出隊：inline int pop() { return queue[front++]; }

隊空的條件：inline bool empty() { return front==rear; }

(2) 迴圈佇列

迴圈佇列——把鏈狀的佇列變成了一個環狀佇列。與上面的鏈狀佇列相比，可以節省很大空間。

定義：int queue[N], front=0, rear=0;
front指向佇列首個元素，rear指向佇列尾部元素的右側。

入隊：inline void push(int a) { queue[rear]=a; rear=(rear+1)%N; }

出隊：inline int pop() { int t=queue[front]; front=(front+1)%N; return t; }

隊滿或隊空的條件：inline bool empty() { return front==rear; }
隊滿和隊空都符合上述條件。怎麼把它們區分開呢？
第一種方法：令佇列的大小是N+1，然後只使用N個元素。這樣隊滿和隊空的條件就不一樣了。
第二種方法：在入隊和出隊同時記錄佇列元素個數。這樣，直接檢查元素個數就能知道佇列是空還是滿。

(3) BFS和佇列

BFS要藉助佇列來完成，並且，將佇列改成堆疊，BFS就變成了DFS。BFS的具體實現見42頁「3.7　程式碼模板」。

四.二元樹

(1) 二元樹的連結串列儲存法

struct node
{
    int value;
    node *leftchild, *rightchild;
    //int id;                // 結點編號。
    //node *parent;        // 指向父親結點。
} arr[N];
int top=-1;
node * head = NULL;
#define NEW(p)  p=&arr[++top]; p->leftchild=NULL;        \
                        p->rightchild=NULL; p->value=0

(2) 完全二元樹的一維陣列儲存法

　　如果一個二元樹的結點嚴格按照從上到下、從左到右的順序填充，就可以用一個一維陣列儲存。

下面假設這個樹有n個結點，待操作的結點是r（0≤r＜n）。

操作	宏定義	r的取值範圍
r的父親	#define parent(r) (((r)-1)/2)	r≠0
r的左兒子	#define leftchild(r) ((r)*2+1)	2r＋1＜n
r的右兒子	#define rightchild(r) ((r)*2+2)	2r＋2＜n
r的左兄弟	#define leftsibling(r) ((r)-1)	r為偶數且0＜r≤n-1
r的右兄弟	#define rightsibling(r) ((r)+1)	r為奇數且r＋1＜n
判斷r是否為葉子	#define isleaf(r) ((r)>=n/2)	r＜n

(3) 二元樹的遍歷

1. 前序遍歷

void preorder(node *p)
{
    if (p==NULL) return;

    // 處理結點p
    cout<<p->value<<' ';
    
    preorder(p->leftchild);
    preorder(p->rightchild);
}

2. 中序遍歷

void inorder(node *p)
{
    if (p==NULL) return;

    inorder(p->leftchild);

    // 處理結點p
    cout<<p->value<<' ';
    
    inorder(p->rightchild);
}

3. 後序遍歷

void postorder(node *p)
{
    if (p==NULL) return;

    postorder(p->leftchild);
    postorder(p->rightchild);

    // 處理結點p
    cout<<p->value<<' ';
}

假如二元樹是通過動態記憶體分配建立起來的，在釋放記憶體空間時應該使用後序遍歷。

4. 寬度優先遍歷（BFS）

首先存取根結點，然後逐個存取第一層的結點，接下來逐個存取第二層的結點……

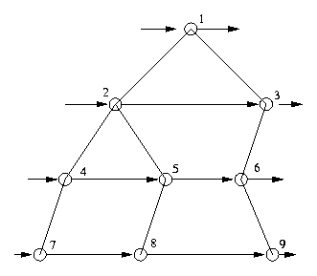
node *q[N];
void BFS(node *p)
{
    if (p==NULL) return;
    
    int front=1,rear=2;
    q[1]=p;
    while (front<rear)
    {
        node *t = q[front++];
        // 處理結點t
        cout<<t->value<<' ';
        
        if (t->leftchild!=NULL) q[rear++]=t->leftchild;
        if (t->rightchild!=NULL) q[rear++]=t->rightchild;
    }
}

對於完全二元樹，可以直接遍歷：

for (int i=0; i<n; i++) cout<<a[i]<<' ';

(4) 二元樹重建

【問題描述】二元樹的遍歷方式有三種：前序遍歷、中序遍歷和後序遍歷。現在給出其中兩種遍歷的結果，請輸出第三種遍歷的結果。

【分析】

前序遍歷的第一個元素是根，後序遍歷的最後一個元素也是根。所以處理時需要到中序遍歷中找根，然後遞迴求出樹。

注意！輸出之前須保證字串的最後一個字元是'\0'。

1. 中序＋後序→前序

void preorder(int n, char *pre, char *in, char *post)
{
    if (n<=0) return;
    int p=strchr(in, post[n-1])-in;
    pre[0]=post[n-1];
    preorder(p, pre+1, in, post);
    preorder(n-p-1, pre+p+1, in+p+1, post+p);
}

2. 前序＋中序→後序

void postorder(int n, char *pre, char *in, char *post)
{
    if (n<=0) return;
    int p=strchr(in, pre[0])-in;
    postorder(p, pre+1, in, post);
    postorder(n-p-1, pre+p+1, in+p+1, post+p);
    post[n-1]=pre[0];
}

3. 前序＋後序→中序

「中＋前」和「中＋後」都能產生唯一解，但是「前＋後」有多組解。下面輸出其中一種。

bool check(int n, char *pre, char *post)        // 判斷pre、post是否屬於同一棵二元樹
{
    bool b;

    for (int i=0; i<n; i++)
    {
        b=false;
        for (int j=0; j<n; j++)
            if (pre[i]==post[j])
            {
                b=true;
                break;
            }
        if (!b) return false;
    }
    return true;
}

void inorder(int n, char *pre, char *in, char *post)
{
    if (n<=0) return;
    int p=1;
    while (check(p, pre+1, post)==false && p<n)
        p++;

    if (p>=n) p=n-1;                // 此時，如果再往inorder裡傳p，pre已經不含有效字元了。
    inorder(p, pre+1, in, post);
    in[p]=pre[0];
    inorder(n-p-1, pre+p+1, in+p+1, post+p);
}

(5) 求二元樹的直徑*

從任意一點出發，搜尋距離它最遠的點，則這個最遠點必定在樹的直徑上。再搜尋這個最遠點的最遠點，這兩個最遠點的距離即為二元樹的直徑。

求樹、圖（連通圖）的直徑的思想是相同的。

// 結點編號從1開始，共n個結點。
struct node
{
    int v;
    node *parent, *leftchild, *rightchild;
} a[1001], *p;
int maxd;
bool T[1003];
#define t(x) T[((x)==NULL)?0:((x)-a+1)]
node *p;
void DFS(node * x, int l)
{
    if (l>maxd) maxd=l, p=x;
    if (x==NULL) return;
    t(x)=false;
    if (t(x->parent)) DFS(x->parent, l+1);
    if (t(x->leftchild)) DFS(x->leftchild, l+1);
    if (t(x->rightchild)) DFS(x->rightchild, l+1);
}

int distance(node *tree)            // tree已經事先讀好
{
    maxd=0;
    memset(T, 0, sizeof(T));
    for (int i=1; i<=n; i++)
        T[i]=true;
    DFS(tree,0);

    maxd=0;
    memset(T, 0, sizeof(T));
    for (int i=1; i<=n; i++) T[i]=true;
    DFS(p,0);

    return maxd;
}

五.並查集

並查集最擅長做的事情——將兩個元素合併到同一集合、判斷兩個元素是否在同一集合中。

並查集用到了樹的父結點表示法。在並查集中，每個元素都儲存自己的父親結點的編號，如果自己就是根結點，那麼父親結點就是自己。這樣就可以用樹形結構把在同一集合的點連線到一起了。

並查集的實現：

struct node
{
    int parent;                        // 表示父親結點。當編號i==parent時為根結點。
    int count;                            // 當且僅當為根結點時有意義：表示自己及子樹元素的個數
    int value;                            // 結點的值
} set[N];

int Find(int x)                            // 查詢演演算法的遞迴版本（建議不用這個）
{
    return (set[x].parent==x) ? x : (set[x].parent = Find(set[x].parent));
}

int Find(int x)                             // 查詢演演算法的非遞迴版本
{
    int y=x;
    while (set[y].parent != y)            // 尋找父親結點
        y = set[y].parent;
    
    while (x!=y)                            // 路徑壓縮，即把途中經過的結點的父親全部改成y。
    {
        int temp = set[x].parent;
        set[x].parent = y;
        x = temp;
    }
    return y;
}

void Union(int x, int y)                // 小寫的union是關鍵字。
{
    x=Find(x); y=Find(y);                // 尋找各自的根結點
    if (x==y) return;                    // 如果不在同一個集合，合併
    
    if (set[x].count > set[y].count)    // 啟發式合併，使樹的高度儘量小一些
    {
        set[y].parent = x;
        set[x].count += set[y].count;
    }
    else
    {
        set[x].parent = y;
        set[y].count += set[x].count;
    }
}

void Init(int cnt)                        // 初始化並查集，cnt是元素個數
{
    for (int i=1; i<=cnt; i++)
    {
        set[i].parent=i;
        set[i].count=1;
        set[i].value=0;
    }
}

void compress(int cnt)                    // 合併結束，再進行一次路徑壓縮
{
    for (int i=1; i<=cnt; i++) Find(i);
}

說明：

使用之前呼叫Init()！

Union(x,y)：把x和y進行啟發式合併，即讓節點數比較多的那棵樹作為「樹根」，以降低層次。

Find(x)：尋找x所在樹的根結點。Find的時候，順便進行了路徑壓縮。
上面的Find有兩個版本，一個是遞迴的，另一個是非遞迴的。

判斷x和y是否在同一集合：if (Find(x)==Find(y)) ……

在所有的合併操作結束後，應該執行compress()。

並查集的效率很高，執行m次查詢的時間約為O(5m)。

六.總結

資料結構是電腦科學的重要分支。選擇合適的資料結構，可以簡化問題，減少時間的浪費。

1. 線性表

線性表有兩種儲存方式，一種是順序儲存，另一種是鏈式儲存。前者只需用一維陣列實現，而後者既可以用陣列實現，又可以用指標實現。

順序表的特點是佔用空間較小，查詢和定位的速度很快，但是插入和刪除元素的速度很慢（在尾部速度快）；連結串列和順序表正好相反，它的元素插入和刪除速度很快，但是查詢和定位的速度很慢（同樣，在首尾速度快）。

2. 棧和佇列

棧和佇列以線性表為基礎。它們的共同點是新增、刪除元素都有固定順序，不同點是刪除元素的順序。佇列從表頭刪除元素，而棧從表尾刪除元素，所以說佇列是先進先出表，堆疊是先進後出表。

棧和佇列在搜尋中有非常重要的應用。棧可以用來模擬深度優先搜尋，而廣度優先搜尋必須用佇列實現。

有時為了節省空間，棧的兩頭都會被利用，而佇列會被改造成迴圈佇列。

3. 二元樹

上面幾種資料結構都是線性結構。而二元樹是一種很有用的非線性結構。二元樹可以採用以下的遞迴定義：二元樹要麼為空，要麼由根結點、左子樹和右子樹組成。左子樹和右子樹分別是一棵二元樹。

計算機中的樹和現實生活不同——計算機裡的樹是倒置的，根在上，葉子在下。

完全二元樹：一個完全二元樹的結點是從上到下、從左到右地填充的。如果高度為h，那麼0～h-1層一定已經填滿，而第h層一定是從左到右連續填充的。

通常情況下，二元樹用指標實現。對於完全二元樹，可以用一維陣列實現（事先從0開始編號）。

存取二元樹的所有結點的過程叫做二元樹的遍歷。常用的遍歷方式有前序遍歷、中序遍歷、後序遍歷，它們都是遞迴完成的。

4. 樹

樹也可以採用遞迴定義：樹要麼為空，要麼由根結點和n（n≥0）棵子樹組成。

森林由m（m≥0）棵樹組成。

二元樹不是樹的一種，因為二元樹的子樹中有嚴格的左右之分，而樹沒有。這樣，樹可以用父結點表示法來表示（當然，森林也可以）。並查集的合併、查詢速度很快，它就是用父結點表示法實現的。

不過父結點表示法的遍歷比較困難，所以常用「左兒子右兄弟」表示法把樹轉化成二元樹。

樹的遍歷和二元樹的遍歷類似，不過不用中序遍歷。它們都是遞迴結構，所以可以在上面實施動態規劃。

樹作為一種特殊的圖，在圖論中也有廣泛應用。

樹的表示方法有很多種。

第一種是父節點表示法，它適合並查演演算法，但不便遍歷。

第二種是子節點表表示法。

第三種是「左兒子右兄弟」表示法。

c++基本資料結構