逍遙自在學C語言 | 位運運算元<<的高階用法

前言

在上一篇文章中，我們介紹了~運運算元的高階用法，本篇文章，我們將介紹<< 運運算元的一些高階用法。

一、人物簡介

• 第一位閃亮登場，有請今後會一直教我們C語言的老師 —— 自在。

• 第二位上場的是和我們一起學習的小白程式猿 —— 逍遙。

二、計算2的整數次冪

• 程式碼範例

#include <stdio.h>
int main() 
{
    int x = 1;
    printf("請輸入2的次方數:");
    scanf("%d",&x);
    int y = 1 << x; 
    printf("\n2的%d次方 = %d\n",x,y);
    return 0;
}

• 執行結果

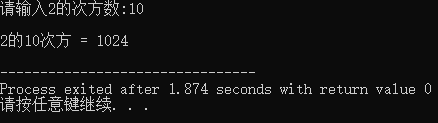
三、將一個位元組序列合併為一個整數

• 例如，將4個位元組組成的位元組序列b合併為一個整數
• 程式碼範例

#include <stdio.h>

int main() 
{
    unsigned char b[4] = {0x12, 0x34, 0x56, 0x78};
    unsigned int x = ((unsigned int)b[0] << 24) | ((unsigned int)b[1] << 16) |((unsigned int)b[2] << 8) | ((unsigned int)b[3]);
    printf("合併後的整數 = 0x%08x\n", x);
    return 0;
}

• 執行結果

下面介紹的兩種用法，會用到& | ^的知識

如果有不清楚的，可以檢視之前的文章：位運運算元的基礎用法

四、標記碼

1、標記位置1

• 例如，將0xF8的第2位(從第0位開始數，由低位到高位) 置1
• 程式碼範例

#include <stdio.h>
int main() 
{
    int x = 0xF8;
    x |= 1<<2; 
    printf("x = 0x%0x\n",x);
    return 0;
}

• 執行結果

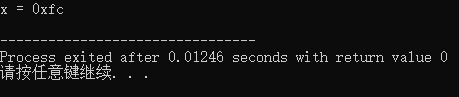
2、標記位置0

• 例如，將0xF8的第3位(從第0位開始數，由低位到高位) 置0
• 程式碼範例

#include <stdio.h>
int main() 
{
    int x = 0xF8;
    x &= (~(1<<3)); 
    printf("x = 0x%0x\n",x);
    return 0;
}

• 執行結果

3、標記位取反

• 例如，將0xF8的第3位和第2位(從第0位開始數，由低位到高位) 取反
• 程式碼範例

#include <stdio.h>
int main() 
{
    int x = 0xF8;
    x ^= (3<<2);  // 3的二進位制為0b11,左移2位剛好對應第2和第3位
    printf("x = 0x%0x\n",x);
    return 0;
}

• 執行結果

五、掩碼

1、末尾連續N位都置1

• 例如，將0xF8的低3位都置1
• 程式碼範例

#include <stdio.h>
int main() 
{
    int x = 0xF8; // Ob1111 1000 
    x |= ((1<<3)-1);
    printf("x = 0x%0x\n",x); // 0b1111 1111
    return 0;
}

• 執行結果

2、末尾連續N位都置0

• 例如，將0xFF的低4位元都置0
• 程式碼範例

#include <stdio.h>
int main() 
{
    int x = 0xFF;	// 0b1111 1111
    x &= ~((1<<4)-1);
    printf("x = 0x%0x\n",x); // 0b1111 0000
    return 0;
}

• 執行結果

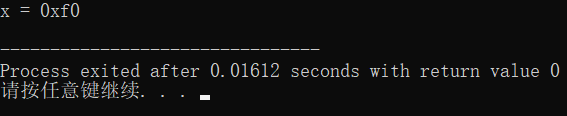
3、末尾連續N位取反

• 例如，將0xFA的低4位元都取反
• 程式碼範例

#include <stdio.h>
int main() 
{
    int x = 0xFA;	// 0b1111 1010
    x ^= ((1<<4)-1);
    printf("x = 0x%0x\n",x); // 0b1111 0101
    return 0;
}

• 執行結果

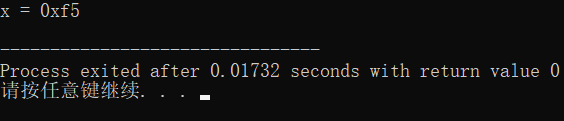
小結

通過這篇文章，我們學會了用位運運算元<<的4種高階用法

1、計算2的整數次冪

2、將一個位元組序列合併為一個整數

3、標記碼

4、掩碼

在下一篇文章中，我們將介紹位運運算元>>的一些高階用法。