論文資訊

論文標題：Adversarial training methods for semi-supervised text classification
論文作者：Taekyung Kim
論文來源：ICLR 2017
論文地址：download 
論文程式碼：download
視屏講解：click

1 背景

1.1 對抗性範例（Adversarial examples）

• 通過對輸入進行小擾動建立的範例，可顯著增加機器學習模型所引起的損失
• 對抗性範例的存在暴露了機器學習模型的脆弱性和侷限性，也對安全敏感的應用場景帶來了潛在的威脅；

　　

1.2 對抗性訓練

　　訓練模型正確分類未修改範例和對抗性範例的過程，使分類器對擾動具有魯棒性

　　目的：

• • 正則化手段，提升模型的效能（分類準確率），防止過擬合
  • 產生對抗樣本，攻擊深度學習模型，產生錯誤結果（錯誤分類）
  • 讓上述的對抗樣本參與的訓練過程中，提升對對抗樣本的防禦能力，具有更好的泛化能力
  • 利用 GAN 來進行自然語言生成 有監督問題中通過標籤將對抗性擾動設定為最大化

1.3 虛擬對抗性訓練

　　將對抗性訓練擴充套件到半監督/無標記情況

　　使模型在某範例和其對抗性擾動上產生相同的輸出分佈

2 方法

2.1 整體框架

　　

　　

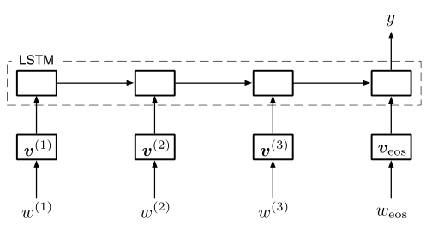
　　基本思想：擴充套件對抗性訓練/虛擬對抗性訓練至文字分類任務和序列模型

　　基本思路：

• 對於文字分類任務，由於輸入是離散的，且常表示為高維one-hot向量，不允許無窮小的擾動，因此將擾動施加於詞嵌入中；由於受干擾的嵌入不能對映至某個單詞，本文中訓練策略僅作為通過穩定分類函數來正則化文字分類器的方法，不能防禦惡意擾動；
• 施加擾動於規範化的詞嵌入中，設定對抗性損失/虛擬對抗性損失，增強模型分類的魯棒性；

2.2 方法介紹

　　將離散單詞輸入轉化為連續向量，定義單詞嵌入矩陣:

 　　　　$\mathbb{R}^{(K+1) \times D}$

　　其中 $K$ 指代單詞數量，第 $K+1$ 個單詞嵌入作為序列 結束($eos$)令牌

　　設定對應時間步長的離散單詞為 $w^{(t)}$  ，單詞嵌入為 $v^{(t)}$ 

　　針對文字分類問題使用 LSTM 模型或雙向 LSTM 模型 由於擾動為有界範數，模型在對抗性訓練過程中可能 通過 「學習具有較大範數的嵌入使擾動變得不重要」 的病態解決方案，因此需將嵌入進行規範化：

　　　　$\overline{\boldsymbol{v}}_{k}=\frac{\boldsymbol{v}_{k}-\mathrm{E}(\boldsymbol{v})}{\sqrt{\operatorname{Var}(\boldsymbol{v})}} \text { where } \mathrm{E}(\boldsymbol{v})=\sum_{j=1}^{K} f_{j} \boldsymbol{v}_{j}, \operatorname{Var}(\boldsymbol{v})=\sum_{j=1}^{K} f_{j}\left(\boldsymbol{v}_{j}-\mathrm{E}(\boldsymbol{v})\right)^{2}$

　　其中 $f_{i}$ 表示第 $i$ 個單詞的頻率，在所有訓練範例中進行計算。

2.2.1 對抗性訓練

　　對抗性訓練嘗試提高分類器對小的、近似最壞情況擾動的魯棒性——使分類器預測誤差最大

　　代價函數：

　　　　$-\log p\left(y \mid \boldsymbol{x}+\boldsymbol{r}_{\mathrm{zd} v} ; \boldsymbol{\theta}\right) \text { where } \boldsymbol{r}_{\mathrm{ud} v}-\underset{\boldsymbol{r}, \mid \boldsymbol{r} \| \leq \epsilon}{\arg \min } \log p(y \mid \boldsymbol{x}+\boldsymbol{r} ; \hat{\boldsymbol{\theta}})$

　　其中 $r$ 為擾動， $\widehat{\theta}$ 為分類器當前引數的常數集，即表明構造對抗性範例的過程中不應該進行反向傳播修改引數

　　對抗性擾動 $r$  的生成：通過線性逼近得到

　　　　$\boldsymbol{r}_{\mathrm{adv}}=-\epsilon \boldsymbol{g} /\|\boldsymbol{g}\|_{2} \text { where } \boldsymbol{g}=\nabla_{\boldsymbol{x}} \log p(y \mid \boldsymbol{x} ; \hat{\boldsymbol{\theta}})$

2.2.2 虛擬對抗性訓練

　　將對抗性訓練應用於半監督學習——使分類器預測的輸出分佈差距最大

　　額外代價：

　　　　$\begin{array}{l}\operatorname{KL}\left[p(\cdot \mid \boldsymbol{x} ; \hat{\boldsymbol{\theta}}) \mid p\left(\cdot \mid \boldsymbol{x}+\boldsymbol{r}_{\mathrm{v} \text {-adv }} ; \boldsymbol{\theta}\right)\right] \\\text { where } \boldsymbol{r}_{\mathrm{v} \text {-adv }}=\underset{\boldsymbol{r},\|\boldsymbol{r}\| \leq \ell}{\arg \max } \mathrm{KL}[p(\cdot \mid \boldsymbol{x} ; \hat{\boldsymbol{\theta}}) \| p(\cdot \mid \boldsymbol{x}+\boldsymbol{r} ; \hat{\boldsymbol{\theta}})]\end{array}$

　　對抗性擾動設定：

　　　　$\boldsymbol{r}_{\mathrm{adv}}=-\epsilon \boldsymbol{g} /\|\boldsymbol{g}\|_{2} \text { where } \boldsymbol{g}=\nabla_{\boldsymbol{s}} \log p(y \mid \boldsymbol{s} ; \hat{\boldsymbol{\theta}})$

　　對抗性損失：

　　　　$L_{\mathrm{adv}}(\boldsymbol{\theta})=-\frac{1}{N} \sum_{n=1}^{N} \log p\left(y_{n} \mid \boldsymbol{s}_{n}+\boldsymbol{r}_{\mathrm{adv}, n} ; \boldsymbol{\theta}\right)$

　　其中 $N$ 為標記樣本的數量

　　虛擬對抗性擾動設定：

　　　　$\boldsymbol{r}_{\mathrm{v} \text {-adv }}=\epsilon \boldsymbol{g} /\|\boldsymbol{g}\|_{2} \text { where } \boldsymbol{g}=\nabla_{\boldsymbol{s}+\boldsymbol{d}} \mathrm{KL}[p(\cdot \mid \boldsymbol{s} ; \hat{\boldsymbol{\theta}}) \mid p(\cdot \mid \boldsymbol{s}+\boldsymbol{d} ; \hat{\boldsymbol{\theta}})]$

　　其中 $d$ 為小隨機向量，實際通過有限差分法和冪迭代計算虛擬對抗性擾動

　　虛擬對抗性訓練損失：

　　　　$L_{\mathrm{V} \text {-adv }}(\boldsymbol{\theta})=\frac{1}{N^{\prime}} \sum_{n^{\prime}=1}^{N^{\prime}} \mathrm{KL}\left[p\left(\cdot \mid \boldsymbol{s}_{n^{\prime}} ; \hat{\boldsymbol{\theta}}\right) \mid p\left(\cdot \mid \boldsymbol{s}_{n^{\prime}}+\boldsymbol{r}_{\mathrm{v}-\mathrm{ndv}, n^{\prime}} ; \boldsymbol{\theta}\right)\right]$

　　其中 $N$ 為標記/未標記樣本的數量之和

3 總結

　　略

4 其他

• 基於梯度的攻擊：    FGSM（Fast Gradient Sign Method)　　PGD(Project Gradient Descent)　　MIM(Momentum Iterative Method)
• 基於優化的攻擊：    CW(Carlini-Wagner Attack)
• 基於決策面的攻擊：  DEEPFOOL