論文資訊

論文標題：Attract, Perturb, and Explore: Learning a Feature Alignment Network for Semi-supervised Domain Adaptation
論文作者：Taekyung Kim
論文來源：2020 ECCV
論文地址：download 
論文程式碼：download
視屏講解：click

1 摘要

　　提出了目標域內的域內差異問題。　　

　　提出了一個 SSDA 框架，旨在通過減輕域內差異來對齊特徵。 本文框架主要由三種方案組成，即吸引、擾動和探索。 首先，吸引方案全域性最小化目標域內的域內差異。 其次，我們證明了傳統的對抗性擾動方法與 SSDA 的不相容性。 然後，我們提出了一種域自適應對抗性擾動方案，該方案以減少域內差異的方式擾動給定的目標樣本。 最後，探索方案通過選擇性地對齊與擾動方案互補的未標記目標特徵，以與吸引方案互補的類方式區域性對齊特徵。 我們對域適應基準資料集（例如 DomainNet、Office-Home 和 Office）進行了廣泛的實驗。 我們的方法在所有資料集上實現了最先進的效能。

2 介紹

　　在本文中，我們引入了一個稱為域內差異的新概念來分析 UDA 和 SSL 方法的失敗並解決 SSDA 問題。 域內差異是 SSDA 問題中的一個長期問題，在標記樣本監督期間出現，但迄今為止從未被討論過。 在 UDA 問題中，對標記源樣本的監督一般不會嚴重影響目標域分佈，但會隱式吸引一些與源特徵相似的可對齊目標特徵。 因此，通過減少域間差異來對齊源域和目標域是合理的。 然而，在 SSDA 問題中，對標記目標樣本的監督強制將相應的特徵及其鄰域吸引到源特徵簇中，這保證了兩個域分佈之間的部分對齊。此外，未標記的目標樣本與已標記的目標樣本相關性較低，受監督的影響較小，最終保持不對齊(Fig. 1中Top一行)。因此，目標域分佈分為對齊的目標子分佈和未對齊的目標子分佈，導致目標域內域內差異。UDA和SSL方法的失敗將在第3節中詳細討論。

　　受此啟發，我們提出了一個 SSDA 框架，該框架通過解決目標域內的域內差異來對齊跨域特徵。 我們的框架側重於增強未對齊目標樣本的可辨別性並調變類原型，即每個類的代表性特徵。 它由三種方案組成，即吸引、擾動和探索，如圖 1 所示。首先，吸引方案通過域內差異最小化將未對齊的目標子分佈與對齊的目標子分佈對齊。 其次，我們討論了為什麼傳統的對抗性擾動方法在 SSDA 問題中無效。 與這些方法不同，我們的擾動方案將目標子分佈擾動到它們的中間區域，以將標籤傳播到未對齊的目標子分佈。 請注意，我們的擾動方案不會破壞已經對齊的目標特徵，因為它還會臨時生成擾動特徵以進行正則化。 最後，探索方案以類感知方式區域性調變原型，與吸引和擾動方案互補。 我們進行了大量實驗，以評估所提出的方法在域適應資料集（如 DomainNet、Office-Home、Office）上的表現，並取得了最先進的效能。 我們還深入詳細地分析了我們的方法。

　　貢獻：

• 我們在 SSDA 問題中引入了目標域內的域內差異問題。
• 我們提出了一個 SSDA 框架，通過三種方案解決域內差異問題，即吸引、擾動和探索。我們在 DomainNet、Office-Home 和 Office 上進行了廣泛的實驗。 我們在各種方法中實現了最先進的效能，包括香草深度神經網路、UDA、SSL 和 SSDA 方法。我們在 DomainNet、Office-Home 和 Office 上進行了廣泛的實驗。 我們在各種方法中實現了最先進的效能，包括香草深度神經網路、UDA、SSL 和 SSDA 方法。qqq
  • 吸引方案通過域內差異最小化將未對齊的目標子分佈與對齊的目標子分佈對齊。
  • 擾動方案將目標子分佈擾動到它們的中間區域，以將標籤傳播到未對齊的目標子分佈。
  • 探索方案以類感知方式區域性調變原型，與吸引和擾動方案互補。
• 我們在 DomainNet、Office-Home 和 Office 上進行了廣泛的實驗。 我們在各種方法中實現了最先進的效能，包括香草深度神經網路、UDA、SSL 和 SSDA 方法。　　

3 域內差異

　　

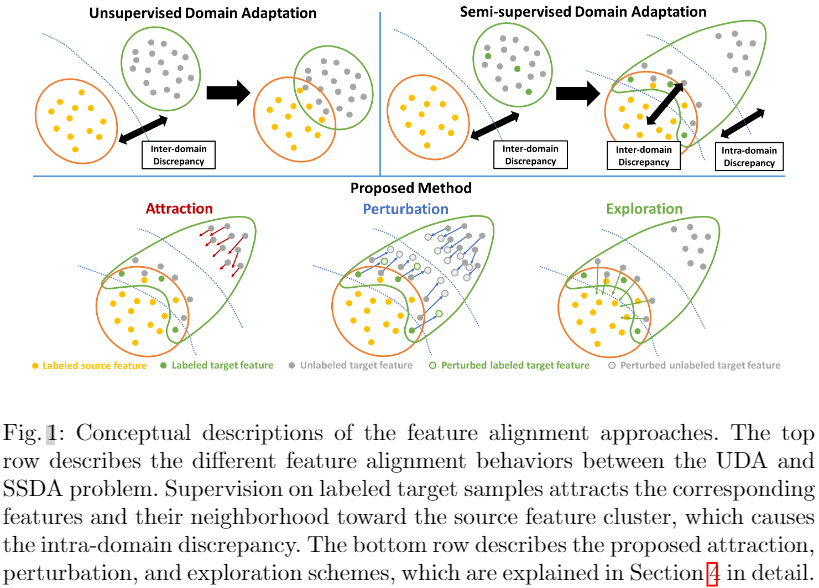
　　域的域內差異是域內子分佈之間的內部分佈差距。 儘管我們在半監督域適應 (SSDA) 問題中展示了域內差異問題，但此類子分佈也可能出現在無監督域適應 (UDA) 問題中，因為通常存在與源叢集對齊的目標樣本。 然而，由於每個域通常在域樣本之間具有獨特的相關性，因此目標域分佈不容易分離成不同的子分佈，最終導致域內差異不足。 因此，傳統的域間差異最小化方法已有效地應用於 UDA 問題。相反，在SSDA 問題，對標記目標樣本的監督強制將目標域確定性地分為對齊的子分佈和未對齊的子分佈。 更具體地說，如 Fig. 1 的第一行所示，標籤的存在將目標樣本及其鄰域拉向每個相應標籤的源特徵簇。 此外，與給定標記目標樣本相關性較低的未標記目標樣本仍然遠離源特徵簇，產生不準確甚至無意義的推理結果。 Fig. 2 演示了目標域中域內差異的存在。 儘管每個類只給出了三個目標標籤，但大量目標樣本已對齊，而錯誤預測的目標樣本 Fig. 2(f)中的紅色圓圈）仍然遠離源域。

　　域內差異的存在使得傳統的域自適應方法不太適合 SSDA 問題。 域自適應的最終目標是增強目標域的可辨別性，這種情況下大部分錯誤發生在未對齊的目標子分佈上。 因此，解決 SSDA 問題取決於未對齊子分佈的對齊程度。 然而，通用域自適應方法側重於減少源域和目標域之間的域間差異，而不考慮目標域內的域內差異。 由於對齊的目標子分佈的存在導致域間差異的低估，域間差異減少方法在 SSDA 問題中的效果較差。 此外，由於對齊的目標子分佈是以類感知方式對齊的，因此這種方法甚至可能產生負面影響。

　　同樣，傳統的半監督學習 (SSL) 方法也存在 SSDA 問題中的域內差異問題。 它源於 SSDA 和 SSL 問題之間的不同假設。 由於 SSL 問題假設從相同分佈中抽樣標記和未標記資料，SSL 方法主要關注將正確的標籤傳播到它們的鄰居。 相反，SSDA 問題假設源域和目標域之間存在顯著的分佈差異，並且標記樣本由源域主導。 由於正確預測的目標樣本與源分佈高度一致，而錯誤預測的目標樣本遠離它們，我們不能再假設這些目標樣本共用相同的分佈。 因此，SSL 方法僅在錯誤預測的子分佈內傳播錯誤，並且由於源域的豐富分佈，在正確預測的子分佈中傳播也毫無意義。 受解釋的啟發，我們提出了一個解決域內差異的框架。

4 方法

4.1 問題表述

　　Let us denote the set of source domain samples by  $\mathcal{D}_{s}=\left\{\left(\mathrm{x}_{i}^{s}, y_{i}^{s}\right)\right\}_{i=1}^{m_{s}}$ . For the target domain,  $\mathcal{D}_{t}=\left\{\left(\mathbf{x}_{i}^{t}, y_{i}^{t}\right)\right\}_{i=1}^{m_{t}}$  and  $\mathcal{D}_{u}=\left\{\left(\mathbf{x}_{i}^{u}\right)\right\}_{i=1}^{m_{u}}$  denote the sets of labeled and unlabeled target samples, respectively. SSDA aims to enhance the target domain discriminability through training on  $\mathcal{D}_{s}$, $\mathcal{D}_{t}$ , and  $\mathcal{D}_{u}$ .

4.2 整體框架

4.3 帶有原型的球形特徵空間

　　在對齊特徵分佈時，確定要適應的特徵空間至關重要。 即使使用相同的方法，效能也可能不會提高，具體取決於應用的特徵空間。 因此，我們在[2]中採用基於相似性的原型分類器來準備合適的特徵空間以更好地適應。 簡而言之，原型分類器輸入歸一化特徵並比較所有類原型之間的相似性，從而減少類內變化作為結果。 對於分類器訓練，我們使用交叉熵損失作為我們的分類損失來訓練具有引數 $\theta$ 的嵌入函數 $f_{\theta}(\cdot) $ 和源域樣本上的原型 $\mathbf{p}_{k}(k=1, \ldots, \mathrm{K})$ 和 標記目標樣本：

　　　　$\begin{aligned}\mathcal{L}_{c l s} & =\mathbb{E}_{(\mathbf{x}, y) \in \mathcal{D}_{s} \cup \mathcal{D}_{t}}[-\log p(y \mid \mathbf{x}, \mathbf{p})] \\& =\mathbb{E}_{(\mathbf{x}, y) \in \mathcal{D}_{s} \cup \mathcal{D}_{t}}\left[-\log \left(\frac{\exp \left(\mathbf{p}_{y} \cdot f_{\theta}(\mathbf{x}) / T\right)}{\sum_{i=1}^{K} \exp \left(\mathbf{p}_{i} \cdot f_{\theta}(\mathbf{x}) / T\right)}\right)\right]\end{aligned}$

　　雖然原型分類器試圖減少標記樣本特徵的類內變化，但所提出的方案側重於對齊歸一化特徵在球形特徵空間上的分佈。

4.4 Attraction Scheme

　　目的：通過域內差異最小化將未對齊的目標子分佈全域性對齊到子分佈級別的對齊目標子分佈。

　　因為，有限數量的標記目標樣本不足以代表對齊目標子分佈的特徵分佈。 因此，由於觀察到對齊的目標子分佈的特徵以類感知方式與源域的特徵高度對齊，本文改為使用標記的源資料和目標資料的複雜分佈。

　　源域資料+帶標記目標資料 全域性對齊 未帶標記的目標資料，對於域內差異的經驗估計，採用最大平均差異（MMD）。因此，球形特徵空間上估計的域內差異可以寫成：

　　　　$\begin{aligned}d\left(\mathcal{D}_{s} \cup \mathcal{D}_{t}, \mathcal{D}_{u}\right) & =\mathbb{E}_{(\mathbf{x}, y),\left(\mathbf{x}^{\prime}, y^{\prime}\right) \in \mathcal{D}_{s} \cup \mathcal{D}_{t}}\left[k\left(f_{\theta}(\mathbf{x}), f_{\theta}\left(\mathbf{x}^{\prime}\right)\right)\right] \\& +\mathbb{E}_{(\mathbf{z}, w),\left(\mathbf{z}^{\prime}, w^{\prime}\right) \in \mathcal{D}_{u}}\left[k\left(f_{\theta}(\mathbf{z}), f_{\theta}\left(\mathbf{z}^{\prime}\right)\right)\right] \\& -2 \mathbb{E}_{(\mathbf{x}, y) \in \mathcal{D}_{s} \cup \mathcal{D}_{t},(\mathbf{z}, w) \in \mathcal{D}_{u}}\left[k\left(f_{\theta}(\mathbf{x}), f_{\theta}(\mathbf{z})\right)\right] \end{aligned}    \quad\quad\quad(2)$

　　其中，$\mathbf{x}^{\prime}$、$\mathbf{z}$ 和 $\mathbf{z}^{\prime}$ 代表樣本，$y^{\prime}$、$w$ 和 $w^{\prime}$ 代表相應的標籤。

　　該方案最小化了域內差異，因此損失可以寫成：

　　　　$L_{a}=d\left(\mathcal{D}_{s} \cup \mathcal{D}_{t}, \mathcal{D}_{u}\right)\quad\quad\quad(3)$

4.5 Perturbation scheme

　　傳統的對抗性擾動是半監督學習 (SSL) 方法之一，在 SSDA 問題中被證明是無效的，甚至會導致負遷移。標記的目標樣本及其鄰域與源域對齊，與不準確的目標樣本分開，導致域內差異。 此時，對齊的特徵已經通過源域的豐富資訊保證了其置信度，而不對齊的特徵只能傳播不準確的預測。 因此，對 對齊和未對齊的目標子分佈的擾動意義不大。

　　與常見的對抗性擾動方法不同，我們的方案將目標子分佈擾動到它們的中間區域，以實現1)從對齊子分佈到未對齊子分佈的精確預測傳播和2)類原型向該區域的調變。這種擾動可以通過搜尋目標特徵的各向異性高熵的方向來實現，因為元素熵隨著特徵遠離原型而增加，而遠離原型的特徵會被吸引到原型上。請注意，微擾方案不會破壞已經對齊的子分佈，因為它在時間上生成了對齊特徵的額外攝動特徵以進行正則化。為了實現這一點，我們首先在熵最大化的方向上擾動類原型。然後，我們優化一個小的有界擾動對擾動原型。最後，通過 KullbackLeibler divergence 對擾動資料和給定資料進行正則化。綜上所述，擾動損失可表示為:

　　　　$\begin{aligned}H_{\mathbf{p}}(\mathbf{x}) & =-\sum_{i=1}^{K} p(y=i \mid \mathbf{x}) \log p(y=i \mid \mathbf{x}, \mathbf{p}) \\r_{\mathbf{x}} & =\underset{\|r\|<\epsilon}{\operatorname{argmin}} \max _{\mathbf{p}} H_{\mathbf{p}}(\mathbf{x}+r) \\\mathcal{L}_{p} & =\mathbb{E}_{\mathbf{x} \in \mathcal{D}_{u}}\left[\sum_{i=1}^{K} D_{K L}\left[p(y=i \mid \mathbf{x}, \mathbf{p}), p\left(y=i \mid \mathbf{x}+\mathbf{r}_{\mathbf{x}}, \mathbf{p}\right)\right]\right] +\mathbb{E}_{(\mathbf{z}, w) \in \mathcal{D}_{t}}\left[\sum_{i=1}^{K} D_{K L}\left[p(y=i \mid \mathbf{z}, \mathbf{p}), p\left(y=i \mid \mathbf{z}+\mathbf{r}_{\mathbf{z}}, \mathbf{p}\right)\right]\right]\end{aligned}$

　　其中 $H_{\mathbf{p}}(\cdot)$ 是根據給定特徵和原型之間的相似性定義的逐元素熵函數，$\mathrm{x}$ 和 $\mathbf{z}$ 代表樣本，$y$ 代表相應的標籤。

4.6 Exploration scheme

　　探索方案旨在以與吸引方案互補的類感知方式區域性調變原型，同時通過與擾動方案互補的適當標準選擇性地對齊未標記的目標特徵。 儘管吸引方案在不考慮原型的情況下在特徵空間上全域性對齊目標子分佈，但它並沒有明確強制對原型進行調變，這可以通過區域性和分類對齊來補充。 另一方面，由於擾動方案對各向異性高熵的擾動特徵進行正則化，擾動特徵及其鄰域的熵逐漸變低。 探索方案對齊這些特徵，使它們的熵變得各向同性，因此對齊的特徵可以被進一步擾動到未對齊的子分佈。 為了實際實現這一點，我們有選擇地收集元素熵小於特定閾值的未標記目標資料，然後應用最近原型類的交叉熵損失。 探索方案的目標函數可以寫成：

　　　　$\begin{aligned}M_{\epsilon} & =\left\{\mathbf{x} \in \mathcal{D}_{u} \mid H_{\mathbf{p}}(\mathbf{x})<\epsilon\right\} \\\hat{y}_{\mathbf{x}} & =\underset{i \in\{1, \ldots, K\}}{\operatorname{argmax}} p(y=i \mid \mathbf{x}, \mathbf{p}) \\\mathcal{L}_{e} & =\mathbb{E}_{\mathcal{D}_{u}}\left[-\mathbf{1}_{M_{\epsilon}}(\mathbf{x}) \log p\left(y=\hat{y}_{\mathbf{x}} \mid \mathbf{x}, \mathbf{p}\right)\right] .\end{aligned}$

　　其中 $M_{\epsilon}$ 是一組熵值小於超引數 $\epsilon$ 的未標記目標資料，$\mathbf{1}_{M_{\epsilon}}(\cdot)$ 是從給定的未標記目標樣本中過濾掉可對齊樣本的指示函數。 

4.7 整體框架和訓練目標

　　我們方法的整體訓練目標是監督損失、吸引力損失、擾動損失和探索損失的加權和。 優化問題可以表述如下：

　　　　$\underset{\mathbf{p}, \theta}{\text{min}} \mathcal{L}_{c l s}+\alpha \mathcal{L}_{a}+\beta \mathcal{L}_{e}+\gamma \mathcal{L}_{p} .$

　　我們將所有方案整合到一個框架中，如圖 3 所示。