開源專案audioFlux: 針對音訊領域的深度學習工具庫
audioFlux是一個Python和C實現的庫,提供音訊領域系統、全面、多維度的特徵提取與組合,結合各種深度學習網路模型,進行音訊領域的業務研發,下面從時頻變換、頻譜重排、倒譜系數、解折積、譜特徵、音樂資訊檢索六個方面簡單闡述其相關功能。
專案地址: https://github.com/libAudioFlux/audioFlux
時頻變換
audioFlux在時頻分析領域中,包含以下通用變換(支援後續所有頻率刻度型別)演演算法:
-
BFT - 基於傅立葉變換。
等效短時傅立葉變換(STFT),一般基於此實現大家熟知的mel頻譜,時域上重疊平移加窗的傅立葉變換,一般重疊變換長度1/4,加高斯窗又稱做Gabor變換,可以調整窗函數長度來方便的模擬時頻分析特點,BFT演演算法除提供標準的mel/bark/erb等頻譜外,還支援mel這些刻度型別的複數譜,同時支援mel等刻度頻譜的重排。
-
NSGT - 非平穩 Gabor 變換。
類似加高斯窗的STFT(短時傅立葉變換),不同之處在於窗函數長度和t建立非平穩關係,相對STFT可以實現穩態訊號中非平穩狀態較好的分析,較好的onset端點偵測效果常基於此類頻譜計算,同時可以做為實現CQT的一種高效方式,本演演算法中NSGT變換的octave頻率刻度型別即CQT的高效實現。
-
CWT - 連續小波變換。
多解析度時頻分析,從數學上看,傅立葉變換的基底是無限的sin/cos函數,而小波變換基底是有限的很小的波函數,波函數的通用表示形式為 $$ \psi_{a,b}(t)=\frac{1}{\sqrt{a}}\psi(\frac{t-b}{a})$$ 其中a決定頻域縮放尺度,b時間平移尺度,建立時頻的自適應分析,相對STFT的固定時頻解析度,具有低頻段頻率分辨高、高頻段時間分辨高特點,非常適合非穩態訊號分析,支援常用的Morse、Morlet、Bump、Pual、Meyer等波函數型別。
-
PWT - 偽小波變換。
基於傅立葉變換實現的類似小波變換效果,CWT的高效演演算法為頻域小波函數計算filterBank和頻域資料做dot運算,如果把小波函數當做一種特殊的窗函數,可以產生類CWT效果,即偽小波變換,如果窗函數建立可調頻帶的引數(庫中尚未實現),可以等效小波變換。
以上變換功能支援下面所有頻率刻度型別:
- linear - 標準線性頻帶頻譜圖,短時傅立葉變換結果取一半即linear刻度頻譜圖,刻度為取樣率/取樣樣本,即最小頻域解析度。
- linsapce - 自定義頻帶範圍的頻譜圖,頻帶可以大於linear頻帶,相當於時域降取樣。
- mel - 梅爾標度頻譜圖,音訊中最常用的頻譜圖型別之一,基於人耳聽覺低頻敏感、高頻不敏感特性,類log壓縮linear刻度。
- bark - 巴克刻度頻譜圖,比梅爾刻度更符合人耳聽覺。
- erb - 等效矩形頻寬頻譜圖,比巴克刻度更符合人耳聽覺。
- octave - 八度刻度頻譜圖,符合樂音對數刻度的頻譜圖。
- log - 對數刻度頻譜圖。
下面是一個BFT變換下不同頻率刻度的簡單對比圖。
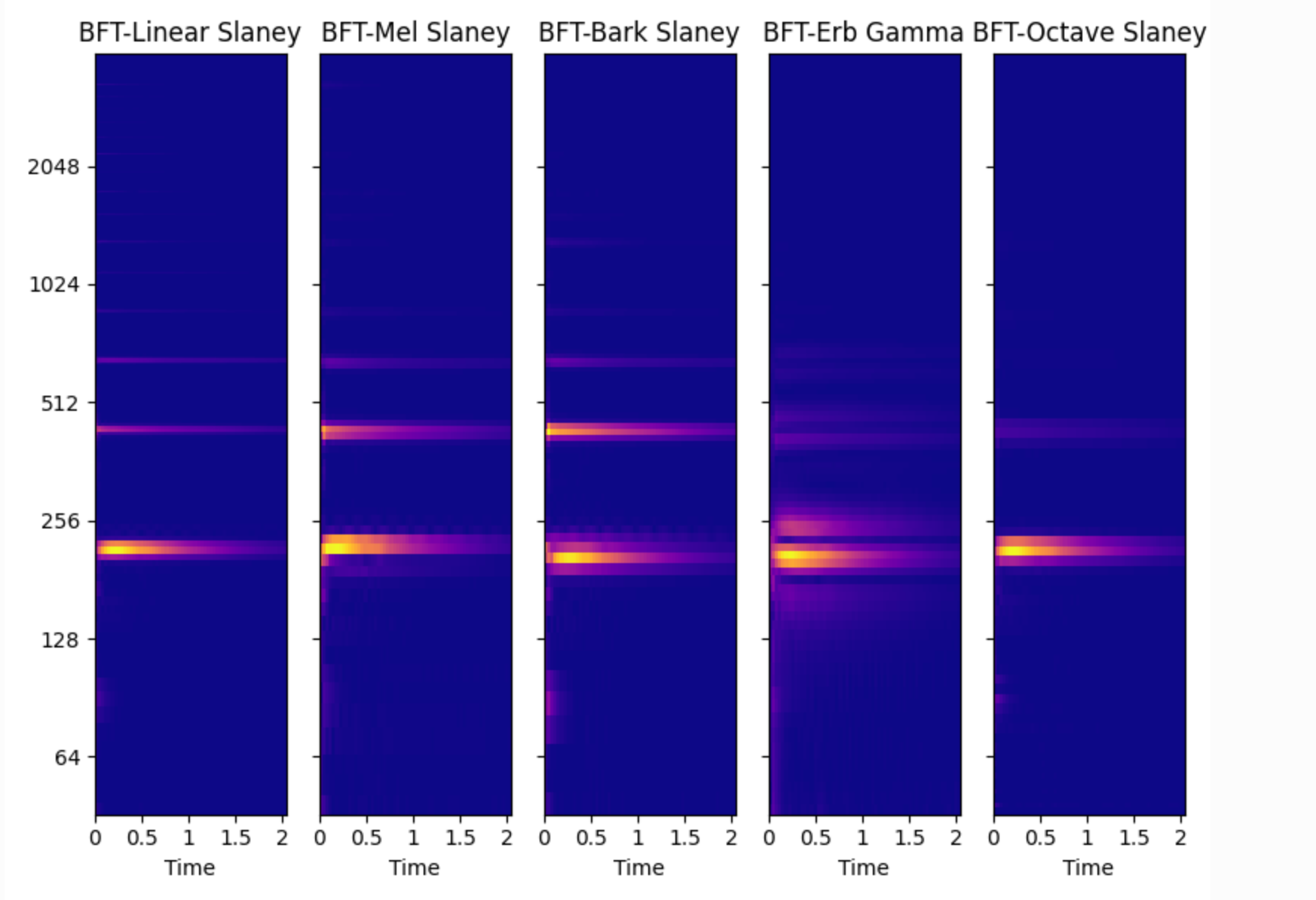
下面是一個CWT不同波函數的簡單對比圖。

以下可用作獨立變換的演演算法有(不支援多種頻率刻度型別):
- CQT - 常數Q變換,頻帶比為常數的變換,音樂中常用的此變換,常基於此計算chroma特徵用於分析和聲。
- VQT - 可變Q變換。
- ST - S變換/Stockwell變換,類似小波變換,是小波變換思想的一種極端特例,可用於偵測分析一些極端的突變訊號如地震、海嘯等,相比NSGT同樣也是加高斯窗,但建立起f和t的縮放關係。
- FST - 快速S變換,S變換的離散基2實現。
- DWT - 離散小波變換,相對CWT而言,頻率基於2的變換。
- WPT - 小波包變換,又稱小波包分解,可以對訊號做細節和近似分解,是訊號分離和合成的一個方式,可用於降噪、模態結構分析等業務。
- SWT - 穩態小波變換,類似小波包變換,分解出的訊號和原訊號長度一致。
下面是一個CQT和NSGT變換下不同刻度的簡單對比圖。
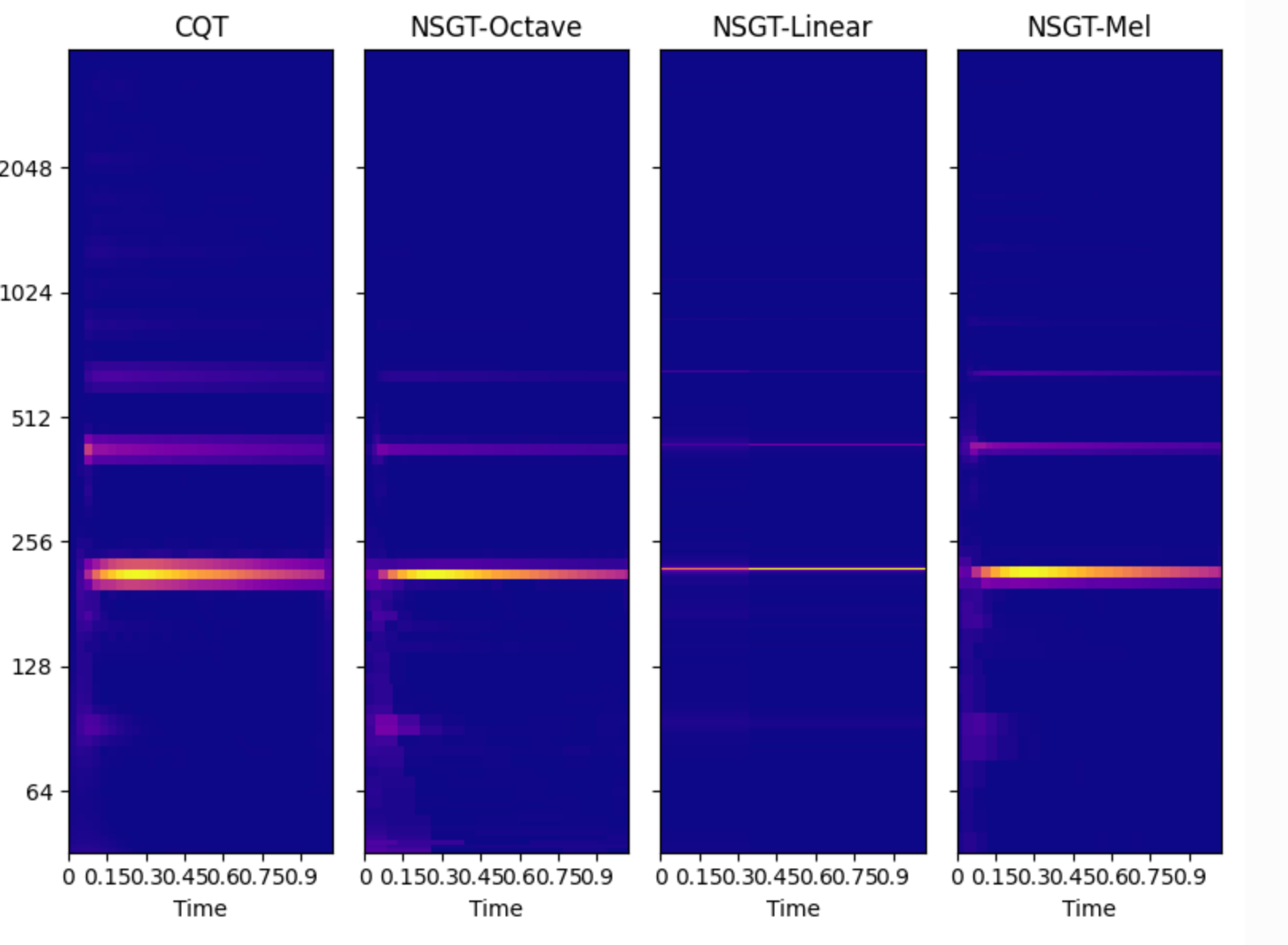
很明顯,NSGT-Octave比CQT要清晰、聚焦一些。
chroma是基於頻譜的更高階特徵,屬於樂音刻度體系範疇,針對非樂音的刻度要差於樂音刻度,目前支援chroma特徵的頻譜型別:
- CQT
- BFT-linear
- BFT-octave
下面是一個Chroma簡單對比圖。
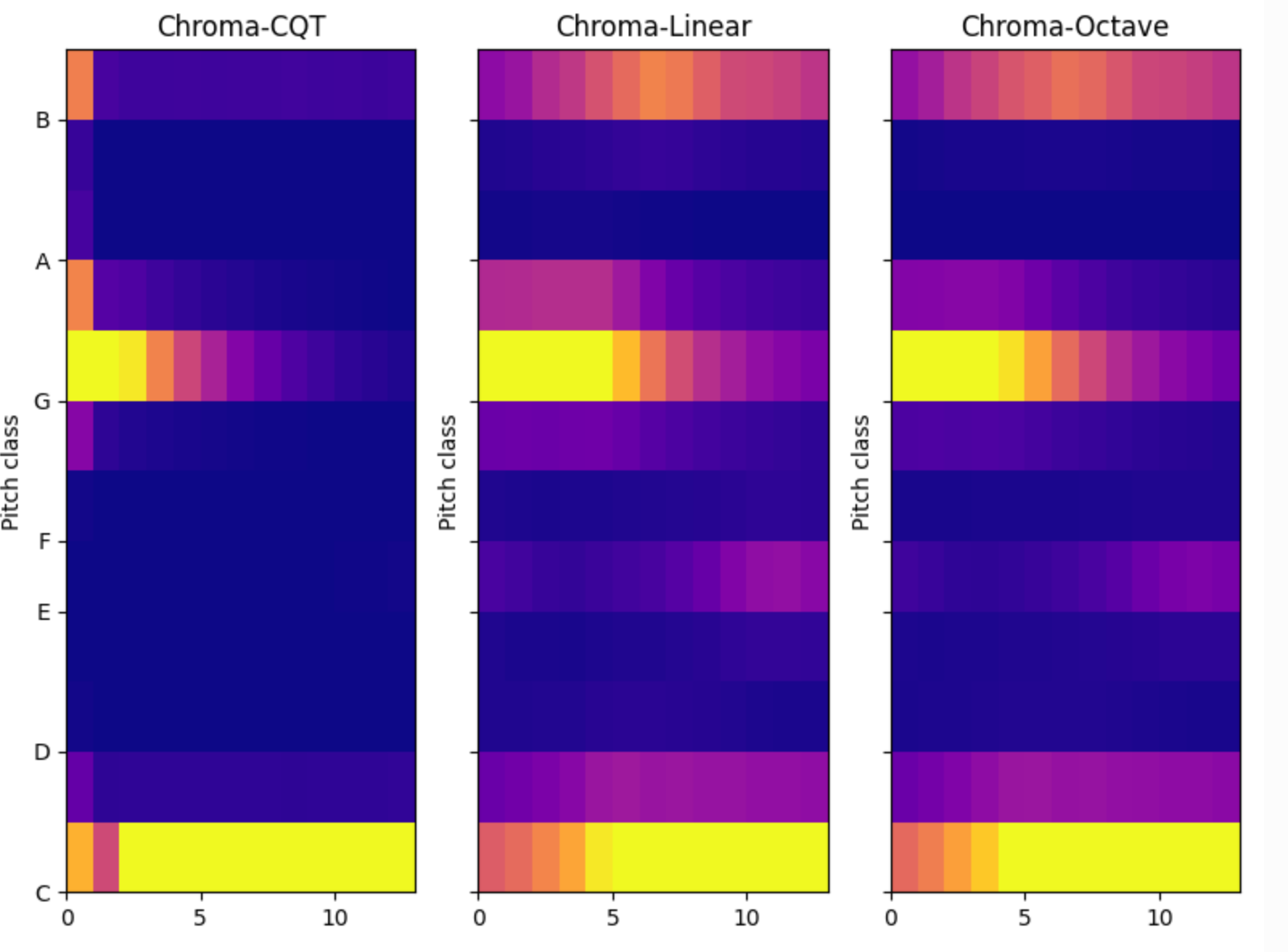
很明顯,CQT-Chroma優於其它頻譜型別下的chroma。
注:
- 不同頻率刻度的頻譜都有各自的應用價值,針對某些業務情況,這些不同刻度頻譜圖可以圖組合起一個大的特徵集合參與網路的訓練。
- 頻譜圖按值的型別abs、平方、log等非線性運算稱為幅值譜、功率譜、對數譜/dB譜,深度學習中一般使用對數譜多一些。
頻譜重排
同步壓縮或重新分配方法是一種用於銳化、高清頻譜圖的技術,可以提升頻譜的清晰度和精度,audioFlux包含以下演演算法:
- reassign - 針對STFT變換重排,基於BFT的mel/bark/erb等頻譜資料同樣實現重排。
- synsq - CWT頻譜資料重排。
- wsst - CWT變換重排。
下面是一個頻譜圖和對應重排後的效果圖。

很明顯,重排後的效果要優於重排前的效果。
可能有人會問,既然重排效果如此好,可以基於上次結果迴圈多次重排嗎?這樣效果如何?audioFlux重排相關演演算法提供多次重排機制,具體效果可以參照檔案做下嘗試對比。
倒譜系數
類似針對mel頻譜的mfcc(梅爾頻率倒譜系數),這個特徵業務上屬於去音高,屬於反映發音物理結構的一個特徵,典型的用於語音識別相關業務,可用於不同樂器分類,結構細化等業務模型訓練。
整個audioFlux專案頻譜體系中,除mfcc以及相應delta/deltaDelta外,支援所有型別的頻譜倒譜系數即xxcc:
- lfcc
- gtcc
- bfcc
- cqcc
- ......
不同頻譜的倒譜系數,都代表著不同頻譜型別的去音高相關,都有各自的應用價值,比如gtcc有論文反映在語音識別業務中音素效果要比mfcc好一些,cqcc針對樂器的分類和一些結構細化業務要遠優於mfcc等等。
下面是針對吉他樂音音訊的不同頻譜倒譜系數的對比圖。

很明顯,在吉他樂音起振階段,cqcc表現最好,後續持續穩定階段,gtcc相比較好。
解折積
在數學中,解折積是折積的逆運算,可以做為訊號分解的一種演演算法,針對頻譜而言,分解後的兩個資料可以表示為formant(共振峰)頻譜圖和pitch頻譜圖,相比mfcc而言,formant是一種更為通識的發音物理結構特徵。
在audioFlux中,支援所有型別頻譜的解折積操作,所發揮的價值在於,針對音高相關的業務,可以去除共振峰干擾後模型推斷更準確;針對結構相關特徵的業務,可以去除音高避免模型的訓練受其干擾。
下面是針對吉他880hz音訊的mel頻譜圖的解折積效果圖。
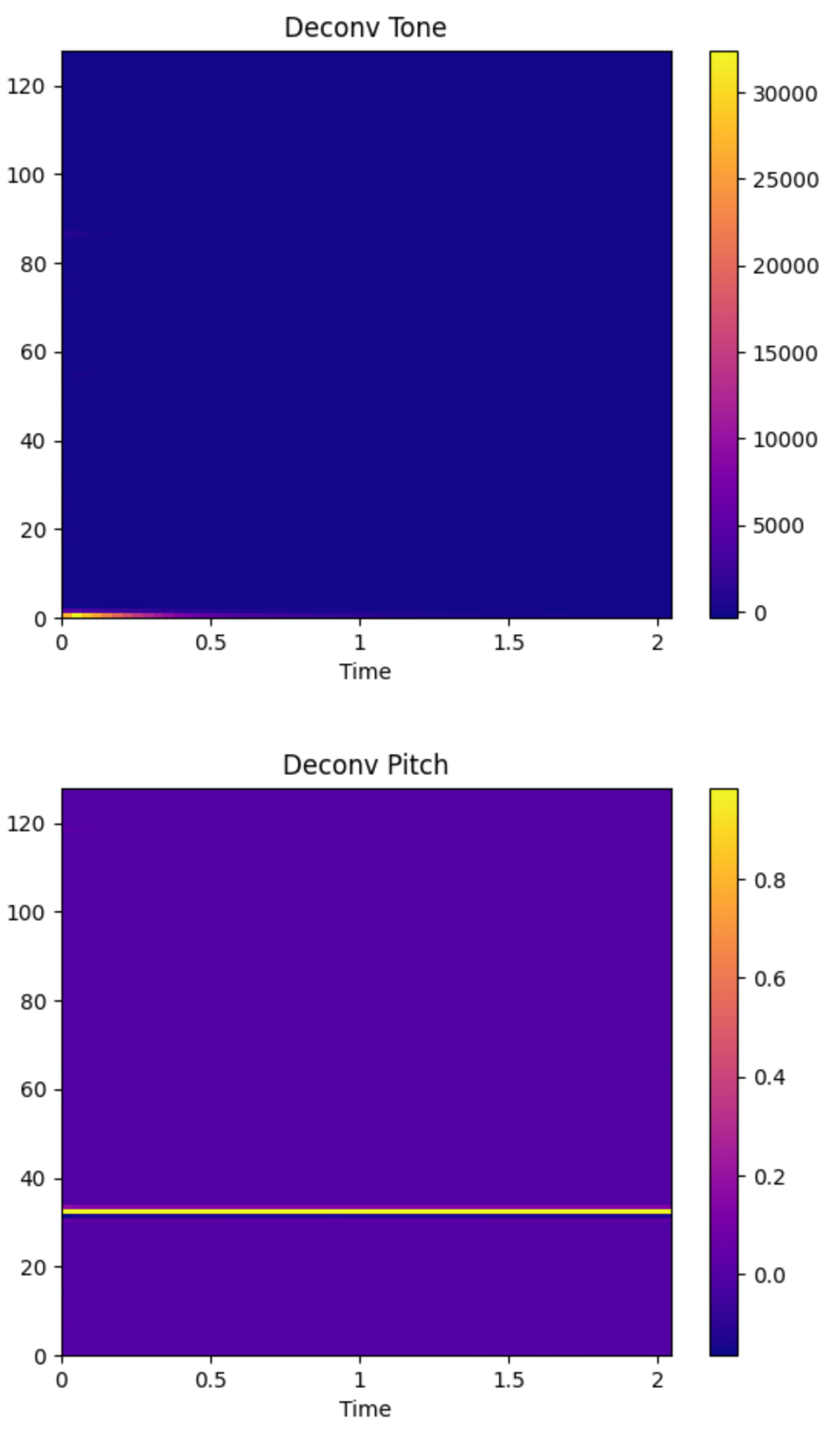
可以看到吉他共振峰部分(音色)和音高部分明顯的分離效果。
譜特徵
在audioFlux中,包括數十種spectral相關的特徵,包括基於音色相關特徵,基於統計相關特徵,基於光譜通量相關特徵,基於奇異值相關特徵,等等。
如:
- flatness
- skewness
- crest
- slop
- rolloff
- ......
- centroid
- spread
- kurtosis
- ......
- flux
- hfc
- mkl
- ......
- ......
等等一小部分,關於audioFlux所提供的所有譜特徵,更具體的功能描述、例子、公式等請參照官方檔案。
下面是一些譜特徵對比圖。

音樂資訊檢索
audioFlux提供mir相關領域pitch估算、onset偵測、hpss(諧波打擊樂分離)等相關業務演演算法。
pitch估算包含基於YIN,STFT等相關演演算法,下面是針對一段人聲練習音高的偵測效果圖。
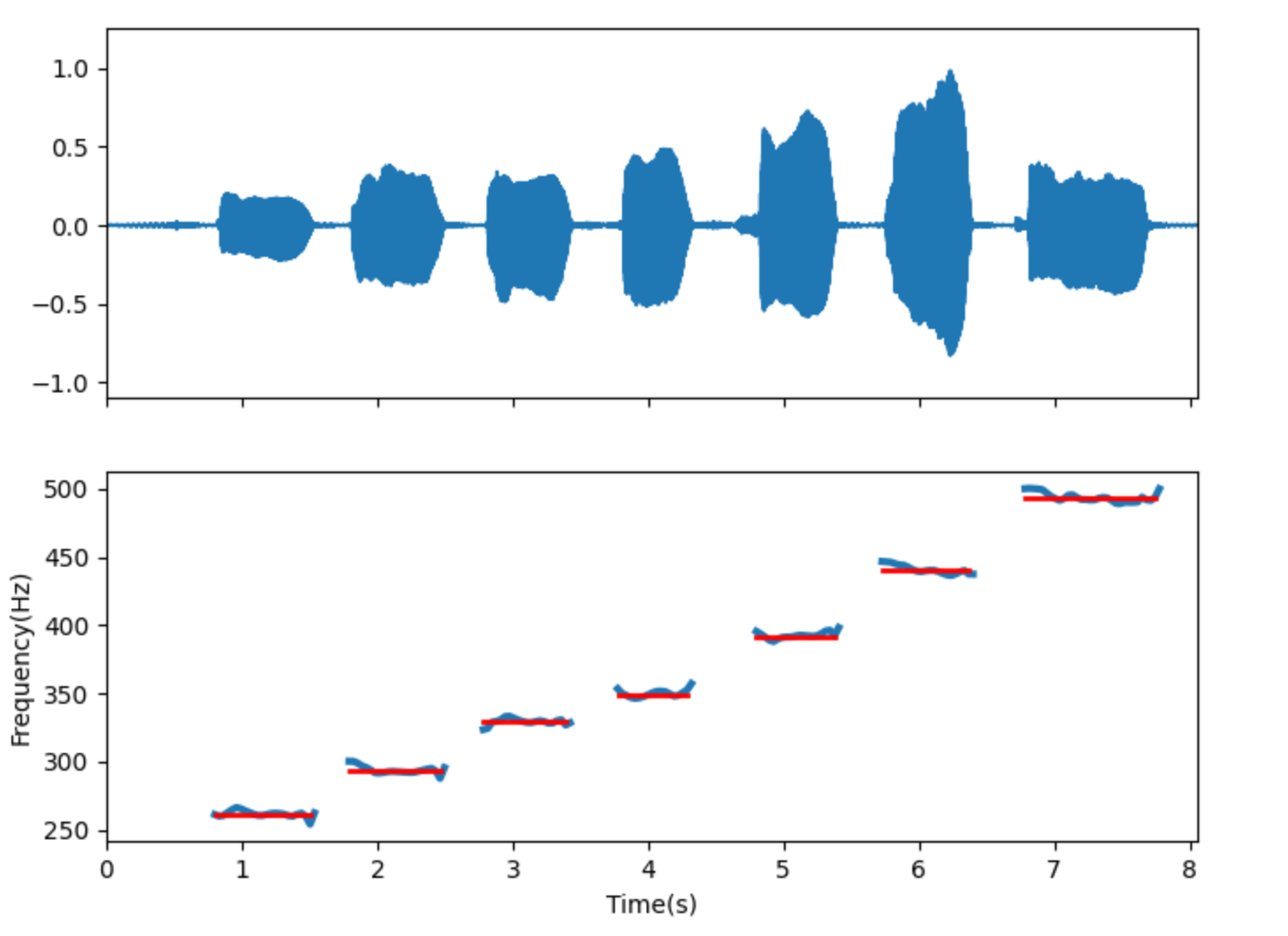
紅色為實際參照音高,藍色為估算音高。
onset偵測包含基於Spectrum flux, novelty等等相關演演算法,下面是一段吉他掃弦伴奏的端點偵測效果圖。
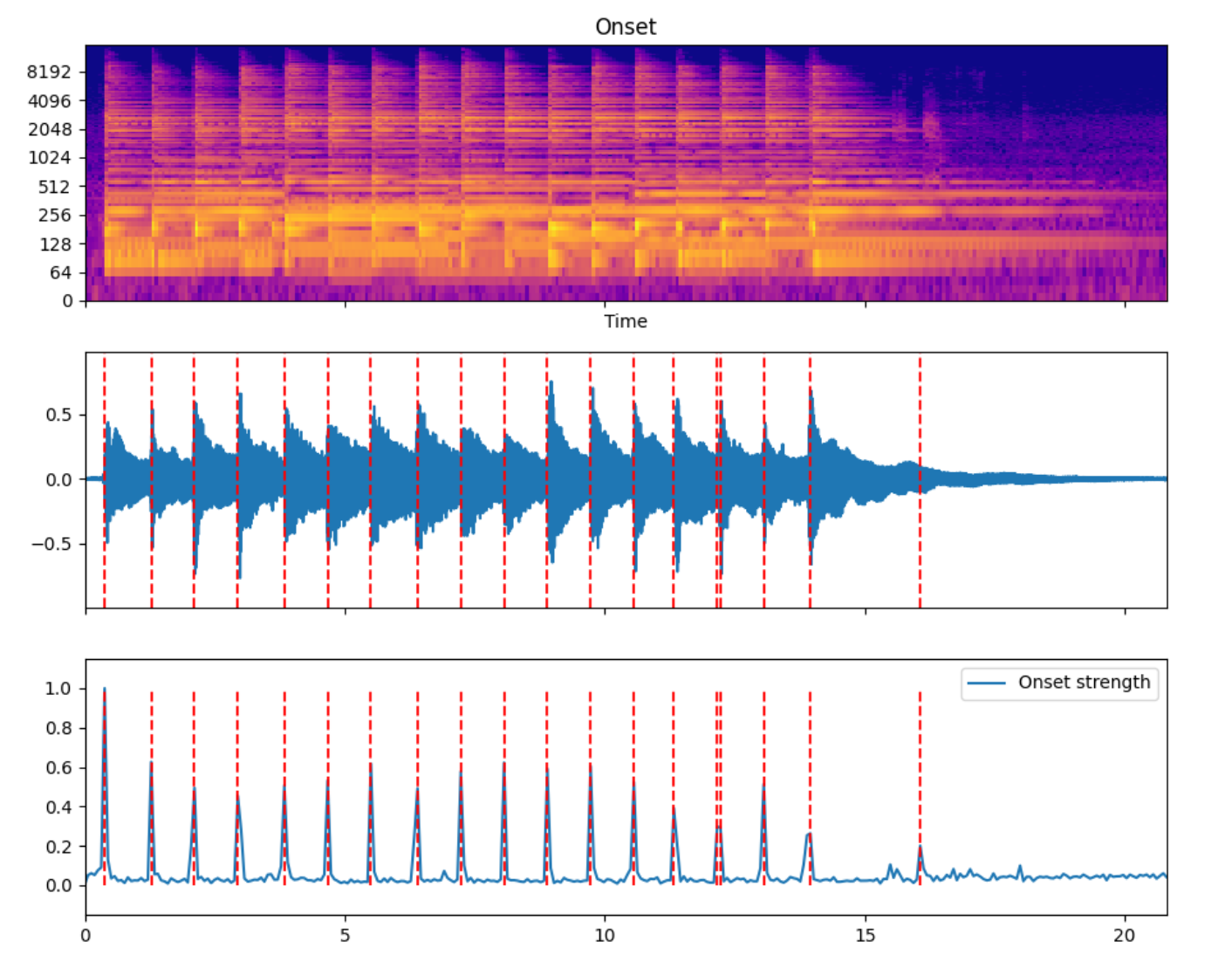
中間時域影象紅色虛線為端點偵測位置疊加而成。
hpss包含中值濾波,非負矩陣分解等(NMF)等演演算法,下面是一段包含吉他彈奏和節拍器音訊的分離效果,上半部分時域效果,下半部分對應頻域效果。

專案地址: https://github.com/libAudioFlux/audioFlux