論文資訊

論文標題：Semi-Supervised Domain Adaptation by Similarity based Pseudo-label Injection
論文作者：Abhay Rawat, Isha Dua, Saurav Gupta, Rahul Tallamraju 
論文來源：Published in ECCV Workshops 5 September 2022
論文地址：download 
論文程式碼：download
視屏講解：click

1 摘要

　　挑戰：半監督域適應 (SSDA) 的主要挑戰之一是標記的源樣本和目標樣本數量之間的比例偏差，導致模型偏向源域；

　　問題：SSDA 最近的工作表明，僅將標記的目標樣本與源樣本對齊可能會導致目標域與源域的域對齊不完整；

2 介紹

　　無監督域適應的基本假設是，學習到域不可知特徵空間的對映，以及在源域上表現足夠好的分類器，可以泛化到目標域。 然而，最近的研究 [20,42,46,7] 表明，這些條件不足以實現成功的域適應，甚至可能由於兩個域的邊緣標籤分佈之間的差異而損害泛化。

　　半監督學習 (SSL) [1,36,3,45] 已被證明在每個註釋的效能方面非常高效，因此提供了一種更經濟的方式來訓練深度學習模型。 然而，一般來說，UDA 方法在半監督環境中表現不佳，在半監督環境中我們可以存取目標域中的一些標記樣本 [31]。 半監督域適應 (SSDA) [35,21,19]，利用目標域中的少量標記樣本來幫助學習目標域上具有低錯誤率的模型。 然而，如 [19] 所示，簡單地將標記的目標樣本與標記的源樣本對齊會導致目標域中的域內差異。 在訓練期間，標記的目標樣本被拉向相應的源樣本簇。然而，未標記的樣本與標記目標樣本的較小相關性被拋在後面。這是因為標記源樣本的數量支配標記目標樣本的數量，導致標籤分佈偏斜。 這導致在目標域的同一類中進行子分佈。 為了減輕來自源域和目標域的標記樣本之間的這種偏差比率，最近的方法 [17,40] 將偽標籤分配給未標記的資料。 但是，這些偽標籤可能存在噪聲，可能導致對目標域的泛化效果不佳。

　　在本文中，我們提出了一種簡單而有效的方法來緩解 SSDA 面臨的上述挑戰。 為了對齊來自兩個域的監督樣本，我們利用對比損失來學習語意有意義和域不變的特徵空間。 為了解決域內差異問題，我們通過將未標記目標樣本的特徵表示與標記樣本的特徵表示進行比較來計算未標記目標樣本的軟偽標籤。 然而，與標記樣本相關性較低的樣本可能會有噪聲和不正確的偽標籤。 因此，我們根據模型對各個偽標籤的置信度，在整個訓練過程中逐漸將偽標記樣本注入（或從）標記目標資料集中（或從中移除）。

3 方法

　　整體框架：

　　

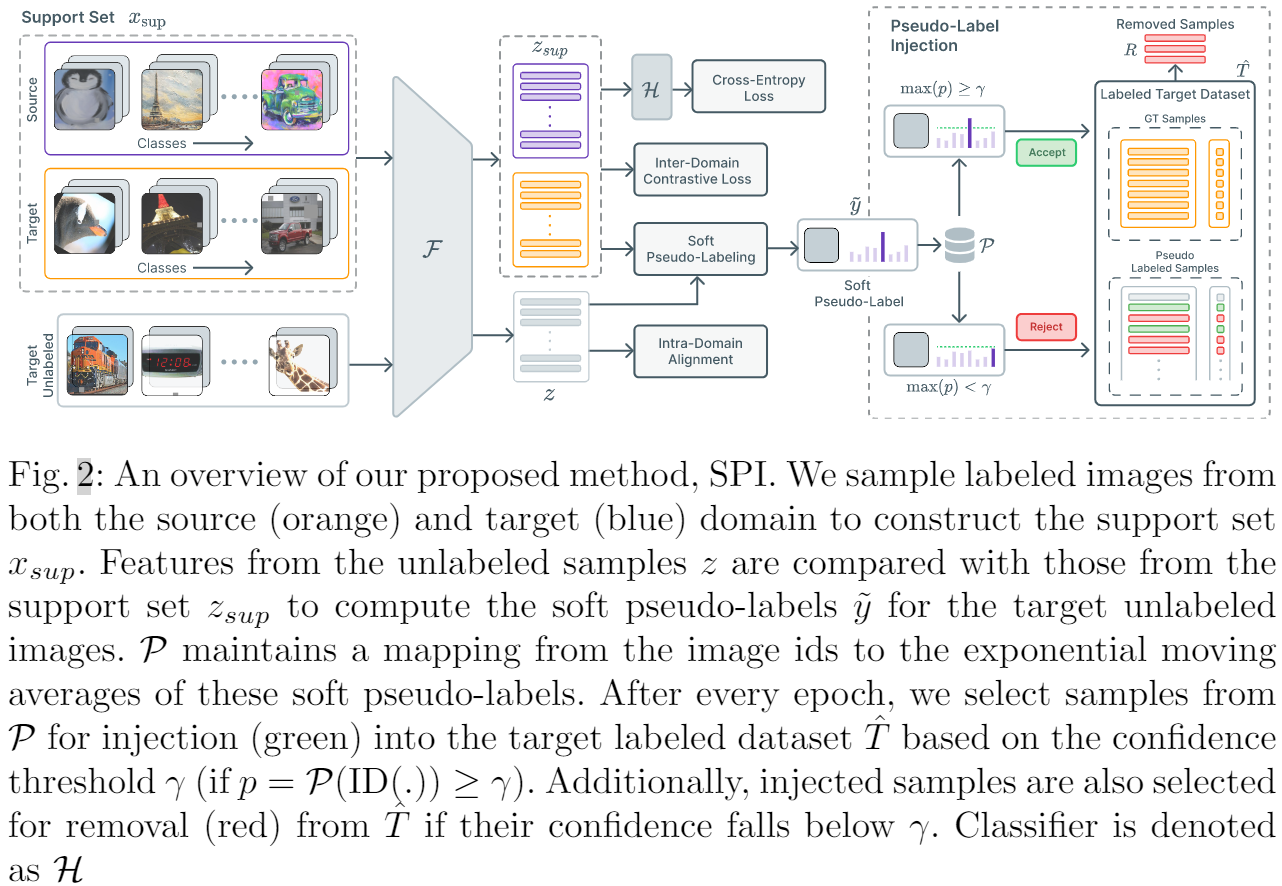
　　Support set：基於小批次，源域、目標域標記樣本每個類包含  $\eta_{\text {sup }}$ 個樣本，所以支援集包含來自兩個域的 $\eta_{\text {sup }} C$ 個樣本，總共 2 個 $\eta_{\text {sup }} C$ 個樣本。

3.1 域間特徵對齊

　　直接地利用對比損失，通過明確地將相同類別的樣本視為正樣本，而不管領域如何。 然後訓練特徵提取器通過最大化同一類特徵之間的相似性來最小化 $\mathcal{L}_{\text {con }}$。

　　　　$\mathcal{L}_{\text {con }}=\sum_{i \in A} \frac{-1}{\left|P_{i}\right|} \sum_{p \in P_{i}} \log \frac{\exp \left(z_{i} \cdot z_{p} / \tau\right)}{\sum_{a \in A \backslash i} \exp \left(z_{a} \cdot z_{p} / \tau\right)} \quad\quad\quad(1)$

　　Note：支撐集之間；

3.2 偽標籤注入

　　然而，正如 [19] 中指出的那樣，對齊來自源域和目標域的標記樣本可能會導致目標域中的子分佈。 即，與目標域中標記樣本相關性較低的未標記樣本不會受到對比損失的影響。 這會導致域內差異，從而導致效能不佳。 為緩解這個問題，本文考慮將未標記的樣本注入標記的目標資料集 ^ T，從而有效地增加目標域中標記樣本的支援。 我們將更詳細地討論這種方法。 3.2.

　　為了減少域內差異，我們建議將未標記目標資料集 $T$ 中的樣本注入標記目標資料集 $\hat{T}$。 使用支援集，首先計算未標記樣本的軟偽標籤。在整個訓練過程中，我們為未標記的目標資料集 $T$ 中的每個樣本保留銳化軟偽標籤的指數移動平均值。 這個移動平均值估計了我們的模型對每個未標記樣本的預測的置信度。 使用這個估計，我們將高度置信的樣本注入到標記的目標資料集 $\hat{T}$ 中，並且在每個時期之後將它們各自的標籤設定為主導類。

　　為了計算來自目標域的未標記樣本的軟偽標籤，我們從 PAWS [1] 中獲得靈感，這是一項半監督學習的最新工作，並將其擴充套件到 SSDA 設定。 我們將支援集 $\mathcal{x}_{sup} $ 及其各自的標籤表示為 $y_{sup}$。 設 $z_{sup}$ 是支援集 $\mathcal{x}_{sup} $ 中樣本的歸一化特徵表示，$\hat{z}_{i}\left(=z_{i} /\left\|z_{i}\right\|\right)$ 表示未標記樣本 $x_i$ 的歸一化特徵表示。 然後，可以使用以下方法計算第 $i$ 個未標記樣本的軟偽標籤：

　　　　$\tilde{y}_{i}=\sigma_{\tau}\left(\hat{z}_{i} \cdot \hat{z}_{\text {sup }}^{\top}\right) y_{\text {sup }}$

　　其中，$\sigma_{\tau}(\cdot)$ 表示帶溫度引數 $\tau$ 的 $\text{softmax}$， 然後使用溫度 $\tau>0$ 的銳化函數 $\pi$ 對這些軟偽標籤進行銳化，描述如下：

　　　　$\pi(\tilde{y})=\frac{\tilde{y}^{1 / \tau}}{\sum_{j=1}^{C} \tilde{y}_{j}^{1 / \tau}}$

　　銳化有助於從未標記和標記樣本之間的相似性度量中產生自信的預測。

　　在整個訓練過程中，我們保持未標記目標資料集 $T$ 中每個影象的銳化軟偽標籤的指數移動平均值 (EMA)。 更具體地說，我們維護一個對映 $\mathcal{P}: \mathbb{I} \rightarrow \mathbb{R}^{C}$ 從未標記樣本的影象 ID 到它們各自銳化的軟偽標籤（類概率分佈）的執行 EMA。 令 $ID(\cdot)$ 表示一個運運算元，它返回與未標記目標資料集 $T$ 中的輸入樣本對應的影象 $ID$，$\mathcal{P}\left(\operatorname{ID}\left(x_{i}\right)\right)$ 是 $x_i$ 的銳化偽標籤的 EMA。 然後，未標記資料集 $T$ 中樣本 $x_i$ 的指數移動平均值更新如下：

 　　　　$\mathcal{P}\left(\mathrm{ID}\left(x_{i}\right)\right) \leftarrow \rho \pi\left(\tilde{y}_{i}\right)+(1-\rho) \mathcal{P}\left(\operatorname{ID}\left(x_{i}\right)\right)   \quad\quad(5)$ 

　　其中 $\rho$ 表示動量引數。 當在訓練過程中第一次遇到一個樣本時，$\mathcal{P}\left(\operatorname{ID}\left(x_{i}\right)\right)$ 被設定為 $\pi\left(\tilde{y}_{i}\right)$ 和  $\text{Eq.5}$ 之後使用。

　　在每個 epoch 之後，我們檢查 $\mathcal{P}$ 中每個樣本的 EMA（類概率分佈）。如果某個特定樣本對某個類的置信度超過某個閾值 $\gamma$，我們將該樣本及其對應的預測類注入到標記的目標資料集 $\hat{T}$ 中。 我們將考慮用於注射 $I$ 的樣本集定義為：

　　　　$I_{t} \triangleq\left\{\left(x_{i}, \arg \max \mathcal{P}\left(\operatorname{ID}\left(x_{i}\right)\right) \mid x_{i} \in T \wedge \max \mathcal{P}\left(\operatorname{ID}\left(x_{i}\right)\right) \geq \gamma\right\}\right.\quad\quad\quad(6)$

　　其中 $t$ 表示當前 $\text{epoch}$。

　　但是，這些樣本可能存在噪音並可能阻礙訓練過程； 因此，如果樣本的置信度低於閾值 $\gamma$，我們也會從標記的資料集中刪除樣本。 要從標記目標資料集 $R$ 中刪除的樣本集定義為：

　　　　$R_{t} \triangleq\left\{\left(x_{i}, y_{i}\right) \mid x_{i} \in\left(\hat{T}_{t} \backslash \hat{T}_{0}\right) \wedge \max \mathcal{P}\left(\operatorname{ID}\left(x_{i}\right)\right)<\gamma\right\}$

　　其中 $y_{i}$ 表示先前分配給方程式中的樣本 $x_i$ 的相應偽標籤。 請注意，來自標記目標資料集 $\hat{T}_{0}$ 的原始樣本永遠不會從資料集中刪除，因為 $I$ 和 $R$ 都僅包含來自未標記目標資料集 $T$ 的樣本。

　　因此，在每個紀元 $t$ 之後，標記的目標資料集 $T$ 將更新為：

　　　　$\hat{T}_{t+1}=\left\{\begin{array}{ll}\left(\hat{T}_{t} \backslash R_{t}\right) \cup I_{t} & \text { if } t \geq W \\\hat{T}_{t} & \text { otherwise }\end{array}\right.$

　　其中 $W$ 表示標記的目標資料集 $\hat{T}$ 保持不變的預熱階段數。 這些預熱時期允許源域和目標域的特徵表示在樣本被注入標籤目標資料集之前在某種程度上對齊。 這可以防止假陽性樣本進入 $\hat{T}$，否則會阻礙學習過程。

3.3 範例級相似度

　　我們現在介紹範例級相似性損失。 受 [1,5] 的啟發，我們遵循多檢視增強來生成未標記影象的 $ηg = 2$ 全域性裁剪和 $ηl$ 區域性裁剪。 這種增強方案背後的關鍵見解是通過明確地使這些不同檢視的特徵表示更接近來強制模型關注感興趣的物件。 全域性裁剪包含更多關於感興趣物件的語意資訊，而區域性裁剪僅包含影象（或物件）的有限檢視。 通過計算全域性作物和支援集樣本之間的特徵級相似度，我們使用 $\text{Eq.3}$ 計算未標記樣本的偽標籤。

　　然後訓練特徵提取器以最小化使用一個全域性檢視生成的偽標籤與使用另一個全域性檢視生成的銳化偽標籤之間的交叉熵。 此外，使用區域性檢視生成的偽標籤與來自全域性檢視的銳化偽標籤的平均值之間的交叉熵被新增到損失中。

　　稍微濫用符號，給定樣本 $x_{i}$，我們將 $\tilde{y}_{i}^{g_{1}}$ 和 $\tilde{y}_{i}^{g_{2}}$ 定義為兩種全域性作物的偽標籤，並且 $\tilde{y}_{i}^{l_{j}}$ 表示第 $j$ 個區域性作物的偽標籤。 類似地，我們遵循相同的符號來為這些由 $\pi$ 表示的作物定義銳化的偽標籤。 因此訓練特徵提取器以最小化以下損失：

　　　　$\mathcal{L}_{i l s}=-\sum\limits_{i=1}^{\left|B_{u}\right|}\left(\mathrm{H}\left(\tilde{y}_{i}^{g_{1}}, \pi_{i}^{g_{2}}\right)+\mathrm{H}\left(\tilde{y}_{i}^{g_{2}}, \pi_{i}^{g_{1}}\right)+\sum\limits _{j=1}^{\eta_{l}} \mathrm{H}\left(\tilde{y}_{i}^{l_{j}}, \pi_{i}^{g}\right)\right),$

　　其中，$\mathrm{H}(\cdot, \cdot)$ 表示交叉熵，$\pi_{i}^{g}=\left(\pi_{i}^{g_{1}}+\pi_{i}^{g_{1}}\right) / 2$，$\left|B_{u}\right|$ 表示未標記樣本的數量。

3.4 域內對齊

　　為了確保來自目標域中同一類的未標記樣本在潛在空間中靠得更近，我們使用未標記樣本之間的一致性損失。 由於這些樣本沒有標籤，我們計算未標記樣本之間的成對特徵相似性，以估計它們是否可能屬於同一類。 正如[13]所提出的，如果兩個樣本 $x_i$ 和 $x_j$ 的前 $k$ 個高度啟用的特徵維度的索引相同，則可以認為它們相似。 令 $top-k (z)$ 表示 $z$ 的前 $k$ 個高度啟用的特徵維度的索引集，然後，我們認為兩個未標記的樣本 $i$ 和 $j$ 相似，如果：

 　　　　$\text { top-k }\left(z_{i}\right) \ominus \text { top- } \mathrm{k}\left(z_{j}\right)=\Phi$

　　其中，$z_{i}$ 和 $z_{j}$ 是各自的特徵表示，$\ominus$ 是對稱集差運算元。

　　我們構造一個二元矩陣 $M \in\{0,1\}^{\left|B_{u}\right| \times\left|B_{u}\right|}$ ，$M_{i j}$ 表示未標記 Batch $B_{u}$ 中第 $i$ 個樣本是否與第 $j$ 個樣本相似。使用相似性矩陣 $M$ ，我們計算目標未標記樣本的域內一致性損失 $\mathcal{L}_{i d a}$ 如下：

　　　　$\mathcal{L}_{i d a}=\frac{1}{\left|B_{u}\right|^{2}} \sum_{i=1}^{\left|B_{u}\right|} \sum_{j=1}^{\left|B_{u}\right|} M_{i j}\left\|z_{i}-z_{j}\right\|_{2}$

3.5 分類損失和整體框架

　　我們使用標籤平滑交叉熵 [24] 損失來訓練分類器層。 對於分類器訓練，我們只使用來自標記的源資料集 $S$ 和標記的目標資料集 $\hat{T}$ 的樣本，這些樣本不斷用新樣本更新。

　　　　$\mathcal{L}_{c l s}=-\sum_{i=1}^{2 \eta_{\text {sup }} C} \mathrm{H}\left(h_{i}, \hat{y}_{i}\right)$

　　其中，$h_{i}$ 是預測的類別概率，$H$ 表示交叉熵損失，$\hat{y}_{i}=(1-\alpha) y_{i}+\alpha / C$ 是對應於 $xi$ 的平滑標籤。 這裡，$\alpha$ 是平滑引數，$y_{i}$ 是單熱編碼標籤向量。

　　結合我們提出的方法 SPI、$\mathcal{L}_{\text {con }}$、$\mathcal{L}_{i l s}$ 和 $\mathcal{L}_{i d a$ 中使用的不同損失，產生一個單一的訓練目標：

　　　　$\mathcal{L}_{S P I}=\lambda \mathcal{L}_{c o n}+\mathcal{L}_{i l s}+\mathcal{L}_{i d a}+\mathcal{L}_{c l s}$

4 實驗

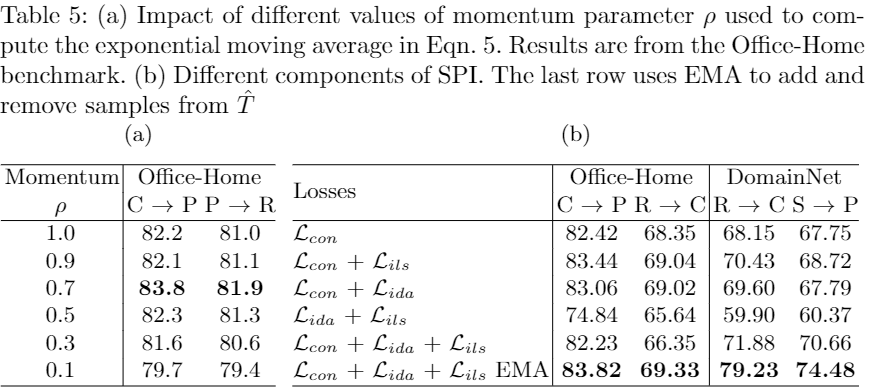
消融研究

　　

5 總結

　　為了對齊兩個域，使用兩個域的監督樣本利用對比損失來來學習語意上有意義和域不可知的特徵空間；

　　為減輕標籤比例偏斜帶來的挑戰，通過將未標記的目標樣本的特徵表示 與 來自源域和目標域的標記樣本的特徵表示進行比較來為未標記的目標樣本打偽標記；

　　為增加對目標域的支援，潛在的噪聲偽標籤在訓練過程中逐漸注入到標記的目標資料集中。 具體來說，使用溫度標度餘弦相似性度量來為未標記的目標樣本分配軟偽標籤。 此外，為每個未標記的樣本計算軟偽標籤的指數移動平均值。 這些偽標籤基於置信度閾值逐漸注入（或移除）到（從）標記的目標資料集中，以補充源和目標分佈的對齊。 最後，在標記和偽標記資料集上使用監督對比損失來對齊源和目標分佈。