博弈補充練習
Nim or not Nim
類似於 NIM 遊戲,有 \(n\) 堆石子,不過每個回合玩家可以從某個堆中刪除任意數量的物件,也可以將堆分成兩個較小的石堆,拿走最後一個石子的人獲勝。
還是一個裸的求 sg 函數的題,但由於範圍過大,肯定不能每次來求sg函數值。
於是需要打表。
發現當 \(x % 4 == 0\) 時,sg(x) = x - 1,當 \(x % 4 == 3\) 時,sg(x) = x + 1,其餘情況下,sg(x) = x。
於是就做完了。
點選檢視程式碼
#include<bits/stdc++.h>
using namespace std;
int getsg(int x){
if(x % 4 == 0)return x - 1;
else if(x % 4 == 3)return x + 1;
return x;
}
int main(){
int T;
scanf("%d",&T);
while(T--){
int a,n,ans = 0;
scanf("%d",&n);
for(int i = 0; i < n; i++){
scanf("%d",&a);
ans = ans ^ getsg(a);
}
if(ans == 0)printf("Bob\n");
else printf("Alice\n");
}
return 0;
}
[AGC017D] Game on Tree
有一棵 \(N\) 個節點的樹,節點標號為 \(1,2,⋯,N\),邊用 \((x_i,y_i)\)表示。 Alice 和 Bob 在這棵樹上玩一個遊戲,Alice先手,兩人輪流操作:
選擇一條樹上存在的邊,把它斷開使樹變成兩個連通塊。然後把不包含 \(1\) 號點的聯通塊刪除
當一個玩家不能操作時輸,你需要算出:假如兩人都按最優策略操作,誰將獲勝。
樣例1:
5
1 2
2 3
2 4
4 5
如圖:
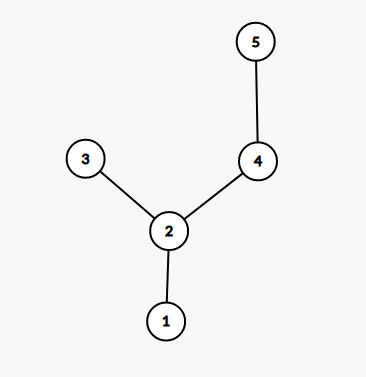
首先注意每棵樹預設根節點為 \(1\),就不需要傻傻地統計點的度數來找根了。。。。
這個題也算是 \(NIM\) 遊戲的翻版,區別就是將模型轉換到圖上了。
對於一個存在分岔的節點,可以類比 \(NIM\) 遊戲中通過互斥或將多組遊戲合併為一個等價的遊戲的結果。如圖中的節點 \(2\),分別斷開 \(2-3\) 和 \(2-4\) 兩條邊,就相當於拆成了兩個子游戲,將兩個遊戲的結果互斥或起來就行了。
類似上述思路,遞迴處理整個圖即可。
點選檢視程式碼
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 2e5;
int n;
vector<int> g[MAXN + 5];
int getsg(int u,int fa){
int ans = 0;
for(int i = 0; i < g[u].size(); i++){
int v = g[u][i];
if(v == fa)continue;
int get = getsg(v,u);
ans ^= (get + 1);//加上刪去的邊
}
return ans;
}
int main(){
scanf("%d",&n);
for(int i = 1; i < n; i++){
int u,v;
scanf("%d%d",&u,&v);
g[u].push_back(v);
g[v].push_back(u);
}
int ans = 0;
ans ^= (getsg(1,1));
if(ans)cout << "Alice";
else cout << "Bob";
}
P2964 [USACO09NOV]A Coin Game S
小 A 和小 B 在玩遊戲。
初始時,有 \(n\) 個硬幣被擺成了一行,從左至右第 \(i\) 個硬幣的價值為 \(c_i\)。
遊戲的規則是,兩人交替從這堆硬幣的左側連續取出若干硬幣,然後將取出的硬幣的價值累加至自己獲得的累計價值中。若對方上次操作取出了 \(k\) 個硬幣,那麼本次自己最多取出 \(k \times 2\) 個硬幣。當沒有硬幣可取時,遊戲結束。
遊戲開始時,由小 A 先動手取硬幣,最多取出 \(2\) 個硬幣。
請求出當雙方都儘可能使自己的累計價值最大的情況下,小 A 能獲得的累計價值最大是多少。
一道博弈\(dp\)的題,剛接觸這類題好像總是不太好下手。因為不明白該怎麼轉移才能保證「雙方都採用最優策略」。
現在看來,陷入這種思維陷阱的原因就是總是站在你所要求得答案的玩家的角度進行思考,又因為兩個玩家的操作是交錯的,如此就造成了侷限性,使你在轉移的時候無法顧及另一方也滿足他的最優策略。
解決方法就是不要只站在一個人的角度思考整盤遊戲,應站在當前進行操作的人的位置思考整個遊戲。後文還會詳細解釋這個思路。
同時,博弈\(dp\)類的題目常常會採用 逆向\(dp\) 的思維方式,這個題就是一個例子。
思考題目,感覺 \(dp\) 過程中描述狀態的重要的兩個因子就是:
- 當前最多能拿的硬幣數量。
- 剩餘的硬幣序列的最前面一個硬幣的下標是從哪裡開始的。
定義狀態為 \(dp[i][j]\) 表示當 \(i\) 以前所有硬幣都拿完時,此時最多能拿多少個硬幣所能獲得的最大價值。
這個思維就是上文所提到的站在遊戲雙方的角度進行思考。如果不是這樣,那麼 \(dp\) 維度中就會引入當前遊戲決策者這一維,十分不利於構建轉移方程,也就使得我們陷入了上文提到的思維陷阱。
然而現在似乎出現了個問題,假設我們從前往後進行 \(dp\),過程中每個人每一步所拿的硬幣數量對於正在進行 \(dp\) 的我們是未知的,小 A 就不一定是拿走最後那個硬幣的人,那麼又怎麼才能確定小 A 所獲得的最大價值對應哪個 \(dp\) 狀態呢?
故這裡就要採用逆向\(dp\)。我們不思考每個人從前往後拿硬幣所能得到的最大價值,轉而思考每個人從後往前放置等價值硬幣所最多能放置的最大價值。這需要稍微修改一下 \(dp\) 狀態。首先將原硬幣序列逆向,定義 \(dp[i][j]\) 表示前 \(i\) 個硬幣被放置,下一步操作最多能放置 \(j\) 個,即這次操作最多能放置 \(2 * j\) 個硬幣時所能取得的最大價值。由於已經將硬幣序列反向了,就可以直接正著 \(dp\) 過去了,這也符合剛才的思路。如此就能保證最後的答案就在 \(dp[n][2]\) 這個狀態中。
下面思考怎麼轉移狀態。
首先記錄一個硬幣序列的字首和 \(sum[i]\)。可以確定的是,每次放置硬幣的最大數量不超過 \(n\)。當前最多放置 \(2 * j\) 個硬幣。
因此可以直接列舉一個範圍在 \(1~2 * j\) 的 \(k\)。又因為我們將硬幣序列反向後 \(dp\),就相當於也把操作序列反向了。於是存在:
又引入了一個 \(k\),就相當於有三維了,時間複雜度為 \(O(n^3)\)。怎麼優化呢。
首先 \(i\) \(j\) 這兩維肯定是要列舉的,考慮優化 \(k\) 這一維。
\(dp[i][j−1]\) 是列舉 \(k\) 從等於 \(1\) 到等於 \(2×(j−1)\) ,在 \(2×(j−1)\) 個 \(sum[i]−dp[i−k][k]\) 中取一個 \(max\) 值。
\(dp[i][j]\) 是列舉 \(k\) 從等於 \(1\) 到等於 \(2×j\) ,在 \(2×j\) 個 \(sum[i]−dp[i−k][k]\) 中取一個 \(max\) 值。
所以可知 \(dp[i][j]\) 是嚴格包含 \(dp[i][j−1]\) 的,我們只需要在 \(dp[i][j−1]\) 的基礎上繼續列舉 \(k=2×j−1\) 和 \(k=2×j\) 這兩種狀態即可。
點選檢視程式碼
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 2e3;
int n,a[MAXN + 5],sum[MAXN + 5],dp[MAXN + 5][MAXN + 5];
int main(){
scanf("%d",&n);
for(int i = 1; i <= n; i++){
scanf("%d",&a[i]);
}
for(int i = n; i >= 1; i--){
sum[n - i + 1] = sum[n - i] + a[i];
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
int k = 2 * j - 1;
dp[i][j] = dp[i][j - 1];
if(k <= i)dp[i][j] = max(dp[i][j],sum[i] - dp[i - k][k]);
if(k + 1 <= i)dp[i][j] = max(dp[i][j],sum[i] - dp[i - k - 1][k + 1]);
}
}
cout << dp[n][1];
}
Varacious Steve
Steve 和他的一個朋友在玩遊戲,遊戲開始前,盒子裡有 \(n\) 個甜甜圈,兩個人輪流從盒子裡抓甜甜圈,每次至少抓 \(1\) 個,最多抓 \(m\) 個。
最後一次將當盒子的甜甜圈抓完的人是這一輪遊戲勝利者,他可以將所有抓到的甜甜圈吃完,另外一個人是這輪的失敗者,他抓到的所有甜甜圈要重新放到盒子裡。
下一輪遊戲由上一輪的失敗者開始抓,遊戲繼續。直到若干輪後,所有的甜甜圈被吃完,遊戲結束。
遊戲的目標是吃到儘量多的甜甜圈。遊戲最開始,由Steve先抓,兩個人均採用最優策略,請問Steve最多可以吃到多少甜甜圈。
也是一道博弈 \(dp\) 呢,只不過用了記搜便於轉移罷了。
分析怎樣描述 \(dp\) 狀態,有如下因子:
- 當前回合一共有多少個甜甜圈供遊戲。
- 該回合決策者已經拿了多少個甜甜圈。
- 上一回合的決策者已經拿了多少個甜甜圈。
於是構建三維 \(dp[i][j][k]\),每一維描述從上到下的三個因子之一。(雖然程式碼中沒這麼寫)同樣的,這也是站在每個操作者的角度進行 \(dp\)。
具體細節見程式碼註釋。
點選檢視程式碼
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e2;
int s[MAXN + 5][MAXN + 5][MAXN + 5],n,m,T;//s就是dp陣列
int get(int tot,int l,int r){//分別對應三維狀態,l為當前決策者拿了多少個甜甜圈
if(tot == 0)return 0;
if(s[tot][l][r])return s[tot][l][r];
int ans = 0;
for(int i = 1; i <= min(m,tot - l - r); i++){
if(tot - l - r - i == 0)ans = max(ans,tot - get(r,0,0));//如果拿完了,就新開一把遊戲
else ans = max(ans,tot - get(tot,r,l + i));//沒拿完的話就繼續
}
return s[tot][l][r] = ans;
}
int main(){
scanf("%d",&T);
while(T--){
scanf("%d%d",&n,&m);
memset(s,0,sizeof s);
int ans;
ans = get(n,0,0);
cout << ans << "\n";
}
}
Play Game
Alice 和 Bob 正在玩遊戲。有兩堆卡片。每堆牌有 \(N\) 張牌,每張牌都有一個分數。他們輪流從兩堆中撿起最上面或最下面的牌,這張牌的分數將新增到他的總分中。Alice 和 Bob 都足夠聰明,他們會撿起牌來獲得儘可能多的分數。你知道 Alice 如果先拿起來能得到多少分數嗎?
分析 \(dp\) 狀態組成因子:
- 牌堆1被拿走若干張牌後當前的左端點 \(l1\) 和右端點 \(r1\)
- 牌堆2被拿走若干張牌後當前的左端點 \(l2\) 和右端點 \(r2\)
四維的狀態,仍採用記憶化搜尋。對每一堆牌記錄一個字首和 \(sum\),便於轉移時快速查詢區間和
點選檢視程式碼
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 20;
int sum1[MAXN + 5],sum2[MAXN + 5],dp[MAXN + 5][MAXN + 5][MAXN + 5][MAXN + 5],n,a[MAXN + 5],b[MAXN + 5],T;
int dfs(int l1,int r1,int l2,int r2){
bool emp1 = l1 > r1,emp2 = l2 > r2;
if(emp1 && emp2)return 0;
if(dp[l1][r1][l2][r2] != -1)return dp[l1][r1][l2][r2];
int ans = 0;
if(!emp1){//假如牌堆1沒被拿空
ans = max(ans,sum1[r1] - sum1[l1 - 1] + sum2[r2] - sum2[l2 - 1] - dfs(l1 + 1,r1,l2,r2));//假如拿牌堆1最下面的一張
ans = max(ans,sum1[r1] - sum1[l1 - 1] + sum2[r2] - sum2[l2 - 1] - dfs(l1,r1 - 1,l2,r2));//假如拿牌堆1最上面的一張
}
if(!emp2){//假如牌堆2沒被拿空
ans = max(ans,sum1[r1] - sum1[l1 - 1] + sum2[r2] - sum2[l2 - 1] - dfs(l1,r1,l2 + 1,r2));//假如拿牌堆2最下面的一張
ans = max(ans,sum1[r1] - sum1[l1 - 1] + sum2[r2] - sum2[l2 - 1] - dfs(l1,r1,l2,r2 - 1));//假如拿牌堆2最上面的一張
}
return dp[l1][r1][l2][r2] = ans;
}
int main(){
scanf("%d",&T);
while(T--){
memset(dp,-1,sizeof dp);
scanf("%d",&n);
for(int i = 1; i <= n; i++){
scanf("%d",&a[i]);
sum1[i] = sum1[i - 1] + a[i];
}
for(int i = 1; i <= n; i++){
scanf("%d",&b[i]);
sum2[i] = sum2[i - 1] + b[i];
}
int ans = dfs(1,n,1,n);
cout << ans << "\n";;
}
}
Moving Pebbles(QWQ)
給你 \(N\) 堆石頭,兩個人玩遊戲. 每次任選一堆,首先拿掉至少一個石頭,然後移動任意個石子到任意堆中。誰不能拿石子了,誰就輸了。請求出哪個玩家存在必勝策略。
不妨先思考一下對於先手來說的必敗態。在這樣的博弈問題中,一般存在一個情形,使得後手能夠完全模仿先手的操作,是一個必敗態。拿到這個題裡面來看,假如當前石堆為 \(n\),且石堆可以被分成 \(x\) 對大小相等的石堆對,那麼就是一個必敗態。
對於其他狀態,先手總可以把它們轉化為一個必敗態,對先手來說這就是一個必勝態。
接下來考慮如何證明必敗態和必勝態之間可以相互轉化。
假如現在有 \(n\) 堆石子,為一個必敗態。對 \(i\) 這堆石子進行操作,它有 \(A_i\) 個石子。顯然隨便拿石子,就可以打破以前兩兩相對的狀態。
假如現在為一個必勝態,所有石堆按從小到大排序。
如果 \(n\) 為奇數,需進行操作,將 \(A_n\) 的石子全部分配出去,使得 \(A_1=A_2\) \(A_3=A_4........\)那麼需要操作的石子為 \((A_2-A_1) + (A_4-A_3) + (A_6 - A_5) + ... + (A_{n-1} - A_{n - 2}) <= A_2 - A_1 + A_4 - A_2 + A_6 - A_4 + ... + A_{n-1} - A_{n - 3} = A_{n-1} - A_1 < A_n\),所以可以完成操作。
如果 \(n\) 為偶數,類比上式,仍可分配下去。得證。
然後直接看初狀態是必勝態還是必敗態就行了。
點選檢視程式碼
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e5;
template<class T>inline void read(T &a){
char c;while(!isdigit(c=getchar()));
for(a=c-'0';isdigit(c=getchar());a=a*10+c-'0');
}
int n,m;
map<int,bool> tag;
int main(){
while(~scanf("%d",&n)){
tag.clear();
int cnt = 0;
for(int i = 1; i <= n; i++){
read(m);
if(tag[m])cnt--,tag[m] = 0;
else ++cnt,tag[m] = 1;
}
if(cnt)cout << "first player\n";
else cout << "second player\n";;
}
}
P5932 [POI1999]多邊形之戰
遊戲在一個有 \(n\) 個頂點的凸多邊形上進行,這個凸多邊形的 \(n-3\) 條對角線將多邊形分成 \(n-2\) 個三角形,這 \(n-3\) 條對角線在多邊形的頂點相交。
三角形中的一個被染成黑色,其餘是白色。雙方輪流進行遊戲,當輪到一方時,他必須沿著畫好的對角線,從多邊形上切下一個三角形。切下黑色三角形的一方獲勝。
- 注:如果連線一個多邊形中任意兩點的線段都完全包含於這個多邊形,則稱這個多邊形為凸多邊形。
遇到乍看來沒有思路的題,畫圖輔助思考不失為一種不錯的方法。
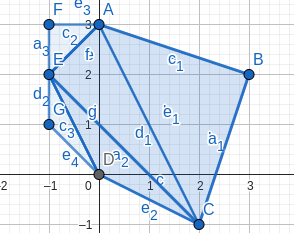
如圖,不難發現,如果要割出一個三角形,就必須把它三個方向的三角形全部刪去。那麼可以知道,在這個遊戲中的必勝態是黑色三角形只有一邊存在三角形。這時只需切一刀就可以割下這個三角形。
假設三角形的三邊所對應的三個方向分別有 \(x\) \(y\) \(z\) 個三角形,只需使其中兩個元素為 \(0\) 即可贏得遊戲。
又由題目知雙方都會採用最優策略,所以肯定不存在黑色三角形的一邊存在大量沒有被割掉的三角形。理想狀況是黑色三角形只有一邊存在一個三角形。
所以先手是否有必勝策略就和 \(x + y + z\) 的奇偶性有關了。若和模 \(2\) 為 \(1\),則先手按最優策略走,就可以實現上文所提到的理想狀況,一刀切下!此時就有必勝策略。若模 \(2\) 為 \(0\),則後手存在必勝策略。
點選檢視程式碼
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e5;
int n,cnt;
bool vis[MAXN + 5];
map<pair<int,int>,int> m;
vector<int> edge[MAXN + 5];
struct TRI{
int a,b,c;
}tri[MAXN + 5];
int main(){
int a,b,c;
scanf("%d%d%d%d",&n,&a,&b,&c);
if(a > b)swap(a,b);
if(a > c)swap(a,c);
if(b > c)swap(b,c);
int x = 0,y = 0,z = 0;
for(int i = 1; i <= n - 3; i++){
int p,q,r;
scanf("%d%d%d",&p,&q,&r);
if(p >= a && p <= b && q >= a && q <= b && r >=a && r <= b)x++;
else if(p >= b && p <= c && q >= b && q <= c && r >= b && r <= c)y++;
else z++;
}
int k = x + y + z;
int j = (x == 0) + (y == 0) + (z == 0);
if(j >= 2)cout << "TAK";
else if(k & 1)cout << "TAK";
else cout << "NIE";
}