強化學習筆記

1.1. 簡介

強化學習（reinforcement learning）是機器學習的一個重要分支，其具有兩個重要的基本元素：狀態和動作。類似於編譯原理中的自動機，或資料結構中的AOE圖，強化學習研究的就是怎樣找到一種最好的路徑，使得不同狀態之間通過執行相應動作後轉換，最終到達目標狀態。先介紹幾個名詞：

• 狀態（狀態的集合一般用 \(S\) 表示，某一狀態標識為 \(s_1,s_2,s_3,...\)）
• 動作（動作的集合一般用 \(A\) 表示，某一狀態標識為 \(a_1,a_2,a_3,...\)）
• 策略（一般用 \(\pi\) 表示）

常見的策略表示主要有兩種不同的形式：函數形式和概率形式。在函數形式中(確定性策略)，策略是一個從狀態空間向動作空間的對映，表示為 \(\pi(s)\rightarrow a\) ,也就是確定了狀態後，就一定要做出什麼動作。在概率形式(隨機性策略)，也是最常見的形式，策略給出的是確定了某一狀態和動作對後，在該狀態下執行該動作的概率，即 \(\pi(s,a)\in (0,1)\)。

強化學習與監督學習有相似之處，但又有著不同。兩者都旨在尋找一種對映，從已知的狀態/屬性推斷出動作/標記，這樣強化學習類似於監督學習中的離散分類器。但強化學習還具有另外的一層特點，即強化學習的反饋往往不能立即獲得，需要與環境的互動、嘗試執行動作後獲得，實際獎賞具有延遲性。一個比較好的例子就是，目前正在研究的路徑規劃問題，即處理碰到障礙物後立即知道獎賞為負數外，小車只用到達最終目標點才能獲得獎賞。因此，強化學習需要通過累積的反饋訊號，不斷的調整策略，最終使其能夠得到「在什麼樣的狀態下選擇什麼樣的動作可以獲得最好的結果。」

1.2. 馬爾科夫決策過程（Morkov Decision Procedure,MDP）

強化學習的模型主要使用馬爾科夫決策過程來描述。先介紹 馬爾科夫性 。定義如下：

定義：狀態\(s_t\)具有馬爾科夫性，當且僅當\(P[s_{t+1} |s_t]=P[s_{t+1} |s_1,s_2,...,s_t]\)

也就是說系統的下一狀態僅與當前狀態有關。若隨機變數序列中的每個狀態都是具有馬爾科夫性，則這個隨機過程就是我們常說的 馬爾科夫隨機過程 。

接著介紹 馬爾科夫過程 ，馬爾科夫過程一般用二元組表示為（S,P），S代表前面提到的「狀態」，P則代表狀態之間的轉移概率。有一系列狀態組成的狀態序列就稱為 馬爾科夫鏈 。

馬爾科夫決策過程 則是在這些概念的基礎上做的延申，是整個強化學習中最基礎的模型。強化學習任務通常可以使用馬爾可夫決策過程（簡稱MDP）來描述：機器處於環境 \(E\) 中，狀態空間為 \(X\) ，其中每個狀態 \(x\in X\) 是機器感知到的環境狀態的描述。機器能採取的動作構成了動作空間 \(A\) ；若某個動作 \(a \in A\) 作用在了當前狀態 \(x\) 上，則潛在轉移函數 \(P\) 將使得環境從當前狀態按某種概率轉移到另一個狀態；在轉移到另一個狀態的同時，環境會根據潛在的「獎賞」（reward）函數 \(R\) 反饋給機器一個獎賞。

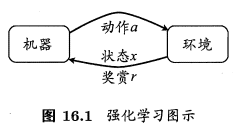
在使用馬爾科夫決策過程來描述強化學習時，可以使用四元組來描述，即 \((X,A,P,R)\) 。另外，有些材料在介紹強化學習時會以五元組來表示，另外多出來的一元常指的是 折扣因子 \(\gamma\) 或 步長 \(T\) 。折扣因子 \(\gamma\) 是一個位於 \((0,1)\) 的引數，有時也被稱為學習率，用於一步步折損累計獎賞值。步長 \(T\) 則限定了機器能夠最多獲得多少步前的獎賞值。兩者是影響強化學習策略收斂的影響之一，稍後介紹到 貝爾曼（Bellman）等式時就能對兩者的作用有更直觀的瞭解。

1.3. 強化學習的分類

瞭解了前面介紹的強化學習最基本概念後，為了更加清晰的分清、認識強化學習的不同演演算法，需要了解強化學習中的分類。這裡分類的標準主要是針對「在狀態空間和動作空間有限的情況下，能否從環境中獲得足夠的資訊」這個問題。據此，強化學習任務可分為 有模型學習 和 無模型學習 。

對多部強化學習任務，我們將任務對應的馬爾可夫決策過程四元組 \(E=(X,A,P,R)\) 均為已知的稱為 有模型學習 ，即機器已經對環境進行了建模，能夠在機器內部模擬出於環境相同或相似的狀況。此時機器能夠知道 狀態\(x\) 執行 動作\(a\) 後轉移到 狀態\(x'\) 的概率，以及轉移所帶來的獎賞值。

對於環境轉移概率、獎賞函數未知的任務，則為 無模型學習 。

有模型學習 是較為簡單的強化學習任務，只需使用貝爾曼(Bellman)等式不斷做「策略評估-策略優化」即可。而 無模型學習 則因為還需要進一步探索環境來獲取獎賞值，所以還牽扯到一個「利用-探索」的問題，相較而言更為複雜。

此外，根據在迭代過程中是否是對策略直接進行改進，還可將強化學習分為 同策略（on-policy） 和 異策略（off-policy） 強化學習。

同策略（on-policy） 是指進行改進和探索的是相同的一個策略，可以形象的理解為想到什麼就做什麼，直接按照自己的想法進行嘗試。

異策略（off-policy） 是指學習時改進和探索使用的是不同的策略。可形象的理解為，在做出一個決策時僅在腦海中模擬出執行某一個動作後的情況，而並不採取直接的行動。

所以從整體效果上來說，雖然兩者最終都會得到最優策略，但是在策略的探索形成過程中，同策略(on-policy)的演演算法相對錶現都較為「膽小/保守」（直接先在當前策略上選動作），而異策略（off-policy）則表現得比較「大膽/冒險」。

1.4. 有模型學習

1.4.1. 策略評估基本指標

強化學習的過程實際上是不斷進行策略優化的過程，因此我們必須對我們已有的策略進行策略評估。一般使用「狀態值函數」(state value function)和「狀態-動作值函數」(state-action value function) 對每一個狀態的價值進行評估。

函數 \(V^{\pi}(x)\) （狀態值函數）表示從狀態 \(x\) 出發，使用策略 \(\pi\) 所帶來的累計獎賞值。（即從當前點一直使用該策略到達終點所獲得的累計獎賞值）。兩種定義如下。

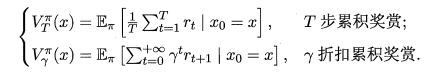
函數 \(Q^{\pi}(x,a)\) （狀態-動作函數）表示從狀態 \(x\) 出發，執行動作 \(a\) 後再使用策略 \(\pi\) 所帶來的累計獎賞。兩種定義如下。

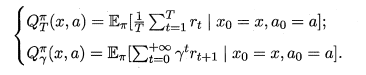
值得說明一下。

• 由於累積回報是個隨機變數，而不是一個確定值，因此無法進行描述。但其期望是個確定值，因此以其期望作為狀體值函數的定義。
• 公式中期望的描述有點像概率論中的條件概率，個人認為是使用了條件期望，故需要學習補充條件期望的定義和運算形狀。
• 公式中涉及兩種形式的 狀態值函數 和 狀態-動作值函數，即「使用\(T\)步累計獎賞」 和 「使用\(\gamma\)折扣累計獎賞」。使用「\(T\)步累計獎賞」時，需給定 \(T\) 的值，用於限定允許最多計算 \(T\) 步內的累計獎賞。使用「\(\gamma\)折扣累計獎賞」時，式子中的 \(\gamma ^t\) 會隨 \(t\) 的增大而值數減小，最終使得後面的獎賞值越來越低，這也也意味著越靠前的獎賞值越重要。

1.4.2. Bellman等式

Bellman等式說白了就是一個遞迴形式的等式，能夠反映 當前狀態的狀態值 以及 上一狀態的狀態值 之間的關係，從而能夠一步步的推知下一狀態值，最終計算出所有的狀態值。

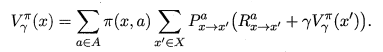
推導上式的過程只需將原式展開，湊出上一狀態的狀態值即可。使用圖來展示推導過程如下圖所示。空心圓圈表示狀態，實心圓圈表示狀態-動作對

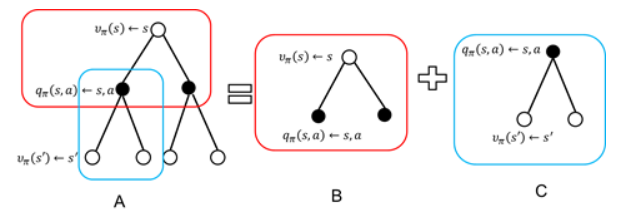
得到了狀態值後，也就可通過下式直接計算出該狀態的狀態-動作值。

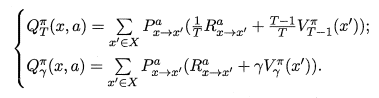
至此就能夠獲取所有的 狀態值 和 狀態-動作值 。

1.4.3. 策略改進與策略迭代

理想的最佳策略應該能使每個狀態的累計獎賞值之和達到最大值，即：

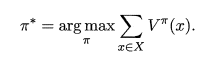
為了能夠得到這個理想的最佳策略，我們需要對原策略進行改進。

最優Bellman等式就揭示瞭如何對現有策略進行改進。最優Bellman等式如下所示：

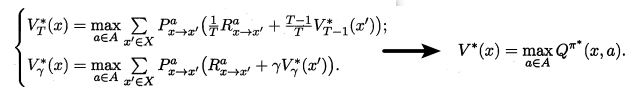
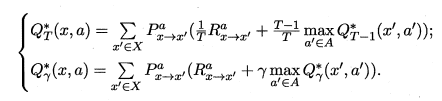
最優Bellman等式改進策略的方式為：將策略選擇的動作改為當前最優的動作，而不是像之前那樣對每種可能的動作進行求和。易知：選擇當前最優動作相當於將所有被選中的概率都賦給累積獎賞值最大的動作，因此每次改進都會使得值函數 單調遞增 ，進而不斷接近最佳策略。進行策略優化的關鍵式子如下所示：

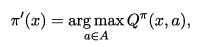
將策略評估與策略改進結合起來，我們便得到了生成最優策略的方法：先給定一個隨機策略，現對該策略進行評估，然後再改進，接著再評估、改進一直到策略收斂、不再發生改變。這便是策略迭代演演算法，演演算法流程如下所示：

1.4.4. 值迭代

仔細思考就可以發現，通過策略改進的方式並不是最好的，因為它是根據最大化狀態-動作函數進行改進，需要不斷的進行策略評估、改進，這會通常比較耗時。

但若從最佳化值函數的角度出發，即先迭代得到最優的值函數，再來計算如何改變策略，便能節省時間，這便是值迭代演演算法，演演算法流程如下所示：

採用 \(\gamma\) 折扣累計獎賞，與 \(T\) 步累計獎賞 相似，只需修改值函數表示式即可。

1.5. 免模型學習

在實際環境中，狀態轉移概率、獎賞函數一般很難得到。在狀態轉移概率 \(P\) 、獎賞函數 \(R\) 均未知的條件下的學習演演算法就是 免模型學習 。

很自然的，在周圍環境未知的情況下，要我們找到一條到達目標點代價最小的路徑，需要我們平衡好 探索 和 利用 的關係。在「探索」時獲知周圍環境執行動作後的代價，在「利用」時選擇花費代價最小的動作。

可以看出，上述 「探索」 和 「利用」 兩種方法是相互矛盾的，僅探索法能較好地估算每個動作的期望獎賞，但是沒能根據當前的反饋結果調整嘗試策略；僅利用法在每次嘗試之後都更新嘗試策略，符合強化學習的思（tao）維（lu），但容易找不到最優動作。因此需要在這兩者之間進行折中。

\(\epsilon\)-貪婪演演算法、Softmax演演算法 是常見的折中方案。

1.5.1. \(\epsilon\)-貪婪演演算法

\(\epsilon\)-貪心 就是基於一個概率來對探索和利用進行折中的方案。具體來說就是以 \(\epsilon\) 的概率進行「探索」（即在所有動作中隨機抽取一個執行），以 \(1-\epsilon\) 的概率進行「利用」（即在已探明的動作中選擇做好的一個動作執行）。\(\epsilon\) 一般取一個較小的值，如0.1，則代表10%的機會會進行「探索」，90%的機會會進行「利用」。

上圖所示的虛擬碼的使用場景是單步強化學習理論模型——— K-搖臂賭博機 。K-搖臂多播及有 K 個搖臂，賭徒在投入一個硬幣後可選擇按下其中一個搖臂，每個搖臂以一定概率吐出硬幣，但這個概率賭徒並不知道。

1.5.2. Softmax演演算法

Softmax演演算法是基於當前每個動作的平均獎賞值來對 「探索」 和 「利用」 進行折中，Softmax函數將一組值（這裡是獎賞值）轉化為一組概率，值越大對應的概率也越高，因此當前平均獎賞值越高的動作被選中的機率也越大。

Softmax 的分佈函數如下所示：

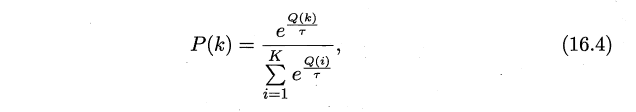
\(Q(k)\) 為記錄當前搖臂的平均獎賞值,\(\tau>0\) 代表溫度，\(\tau\)越小則平均獎賞高的搖臂選中概率越高。

1.5.3. 折中演演算法比較

1.5.4. 免模型學習的分類

免模型依據 「被評估」 和 「被改進」 的是否是同一個策略，可分為 「同策略」（on-policy） 和 「異策略」 （off-policy）學習演演算法。在所有免模型學習演演算法中， 蒙特卡羅強化學習演演算法 是最經典的，其可分為 「同策略蒙特卡羅強化學習演演算法」 以及 「異策略蒙特卡羅強化學習演演算法」。

由於蒙特卡羅強化學習演演算法是通過多次嘗試後，求平均作為期望累計獎賞的近似，它在求平均時類似於「批次處理」，即在一個完整取樣軌跡完成後再對所有狀態-動作對進行更新。若將這個過程改進稱為增量式，就成為了 時序差分學習演演算法 。時序差分學習按同策略、異策略劃分，就成了 Sarsa演演算法 和 Q-學習演演算法

1.5.5. 蒙特卡羅強化學習

所謂蒙特卡羅強化學習，就是在有模型學習的 「策略迭代演演算法」 中增加 \(\epsilon\)-貪心 ，使其同時具有 探索 和 利用 兩方面動作。

與有模型學習不同的是，無模型學習每一次迭代需要先進行一次完整的軌跡取樣。取樣後，才能更新值函數。

同策略蒙特卡羅強化學習 虛擬碼如下所示：

同策略蒙特卡洛強化學習在 策略評估 和 策略改進 時均使用同一個策略實現。若 策略評估 時使用 \(\epsilon\)-貪心，但 策略改進 時卻是改進原來的策略，那麼這種演演算法稱為 異策略蒙特卡羅強化學習 。（可行性分析過程略）

異策略蒙特卡羅強化學習 虛擬碼如下所示：

值得注意的是：

• 使用策略 \(\pi '\) 來評估 策略 \(\pi\) 可以證明實際上只需對累計獎賞加權。可以使用 策略 \(\pi '\) 評估 策略 \(\pi\) 的條件是：策略 \(\pi\)為確定性策略，策略 \(\pi '\) 為 \(\epsilon\)-貪心策略

1.5.6. 時序差分學習演演算法

求期望累計獎賞的近似時，將批次處理形式的「求平均」改為增量式進行，即為時序差分學習演演算法。修改後的累計獎賞值函數如下所示。

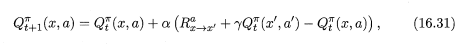
對於該式可以這樣理解：\(\alpha\) 為學習率，式子後半部分相當於一個增量，學習率越大，增量的影響就越大。

下圖所示為 Sarsa演演算法虛擬碼。Sarsa演演算法是一種同策略演演算法。

下圖所示為 Q-學習演演算法虛擬碼。Q-學習演演算法是一種異策略演演算法。

Sarsa演演算法與Q-學習演演算法是兩種非常相似的演演算法，兩者的區別主要在於虛擬碼的第4、5行。Sarsa演演算法會在當前狀態 x 上直接執行策略 \(a = \pi(x)\) ，進入到狀態 \(x'\) ,接著再使用貪心策略 \(a'=\pi^\epsilon(x')\)(即有 \(\epsilon\) 的可能進行隨機探索),即先使用現有策略 \(\pi\) 後使用 \(\pi^\epsilon\)。Q-學習則正好相反，先使用 \(\pi^\epsilon\) 後使用 \(\pi\) 。