漢諾塔與二進位制、滿二元樹的千絲萬縷

漢諾塔(Tower of Hanoi)源於印度傳說中，大梵天創造世界時造了三根金鋼石柱子，其中一根柱子自底向上疊著64片黃金圓盤。大梵天命令婆羅門把圓盤從下面開始按大小順序重新擺放在另一根柱子上。並且規定，在小圓盤上不能放大圓盤，在三根柱子之間一次只能移動一個圓盤。

漢諾塔遞迴演演算法

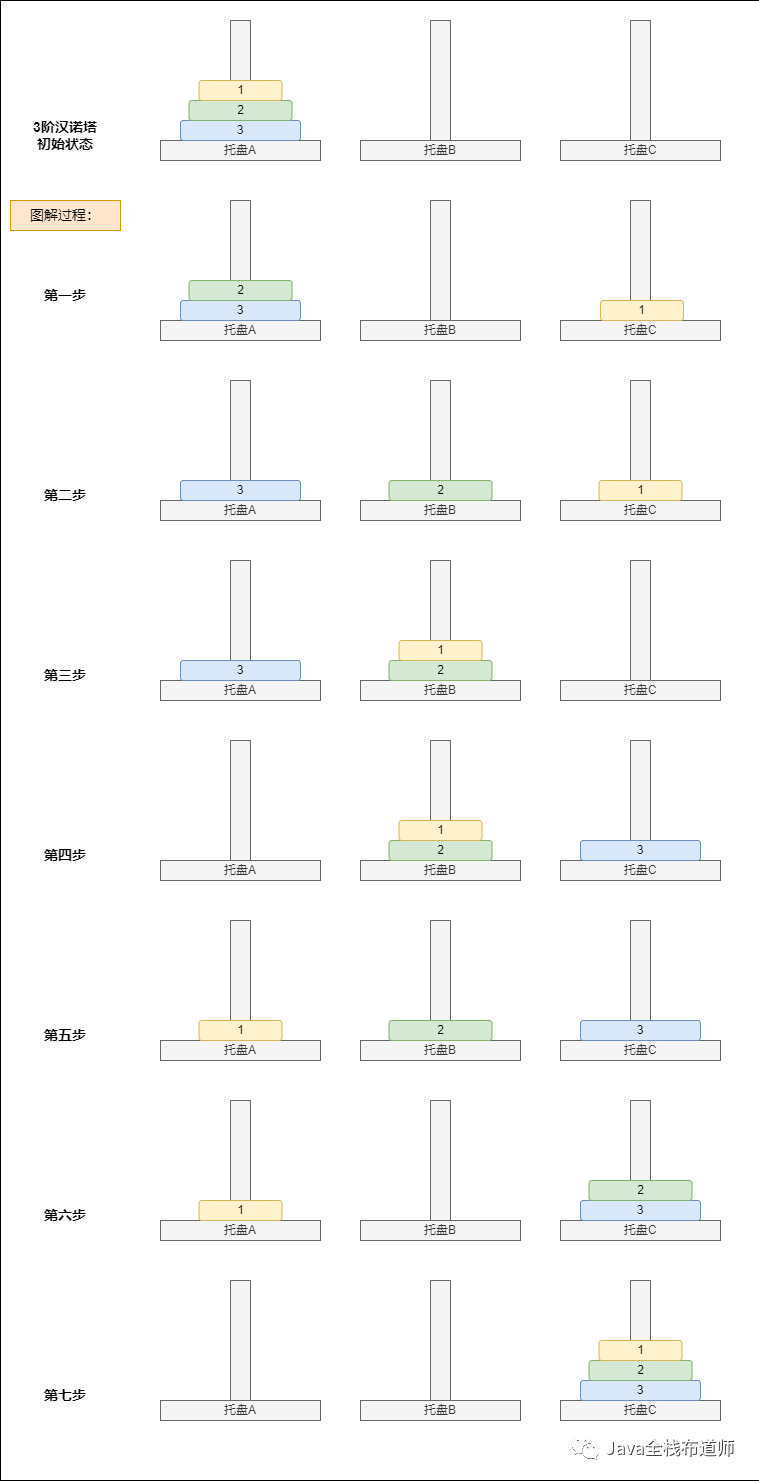
3階漢諾塔移動步驟：

漢諾塔解法思路

一個規模為n的問題，可以拆成互相獨立且與原問題形式相同的子問題的問題，可以採用遞迴方式解決子問題，然後將各個子問題的解合併得到原問題的解（分而治之思想）。

理解過程

如圖，3階的一共需要七步，

因為盤子3是最大的，所以所有盤子都可放在它上面，所以我們可以忽略盤子3，既是把「前三步」看做一個整體，完成2階移動即可，移動目標是從A移動到B（偽C）；

接著執行第四步，從A移到C，此時最大的盤就完成移動了，因為是最大，所以所有盤子都可以移到C，可以忽略盤子3，此時，後續的操作可以將3階看成2階來處理了；

「前三步」將盤子1和2，從A移到B了，托盤A和托盤B是相對來說的，此時的托盤B可以看做是托盤A，所以「後三步」2階移動和普通的2階移動步驟一樣，移動目標是B（偽A）到C。

從上面分析可以知道，所有的移動都是從「A」移動到「C」，只是第一大步和最後一大步是要交換位置，分別是C交換成B、B交換從A（看程式碼不太懂時，回來看這裡）

當n=1時，只需托盤A直接移到托盤C（這是遞迴問題的出口）； 當n>1時，需要藉助另一托盤來移動，將n個圓盤由A移到C上可以分解為以下幾個步驟： (1) 將A上的n-1個圓盤，藉助C，從A移到B上; (2) 把A上第n個圓盤，直接從A移到C上; (3) 將B上的n-1個圓盤，藉助A，從B移到C上。

遞迴方式實現的漢諾塔（Java版）：

public class Hanoi {
    // 階數
    private static int n = 4;
    //驗證漢諾塔移動次數
    private static int sum=0;
    public static void main(String[] args) {
        System.out.println(String.format("%s層漢諾塔的移動順序：", n));
        move(n, 'A','B','C');
        System.out.println("漢諾塔移動次數："+sum);
    }

    /**
     * (n-1) A -> B
     *   n   A -> C
     * (n-1) B -> C
     * 
     * 結束條件為：當n=1 時， A -> C
     */
    public static void move(int n,char A, char B, char C) {
        if(n==1) {
            System.out.println(A + " -> " + C);
            sum++;
        }
        else {
            move(n-1, A, C, B);//每次都是輸出A->C，所以要看到A->B，就需要將B和C交換

            if(n==Hanoi.n)
                System.out.println("前面完成(n-1)層：從A移動到B");
            System.out.println(A + " -> " + C);
            sum++;
            if(n==Hanoi.n)
                System.out.println("完成第(n)層：從A移動到C");

            move(n-1, B, A, C);//每次都是輸出A->C，所以要看到B->C，就需要將A和B交換
            if(n==Hanoi.n)
                System.out.println("前面完成(n-1)層：從B移動到C");
        }
    }

}

執行結果：

3層漢諾塔的移動順序：

A -> C

A -> B

C -> B

前面完成(n-1)層：從A移動到B

A -> C

完成第(n)層：從A移動到C

B -> A

B -> C

A -> C

前面完成(n-1)層：從B移動到C

漢諾塔移動次數：7

先完成(n-1)層：從A移動到B，

再完成第(n)層：從A移動到C，

最後完成(n-1)層：從B移動到C。

通過數學推導漢諾塔移動次數

遞迴演演算法可以通過遞迴式的方式去推導證明，現在通過遞迴式推導漢諾塔移動次數。

假定n是盤子的數量，T(n)是移動n個圓盤的移動次數。

當n=1時，T(1)=1

當n=2時，T(2)=2T(1)+1

當n=3時，T(3)=2T(2)+1

得漢諾塔遞迴式：

由遞迴式求n階漢諾塔移動次數：

由遞迴式可知：

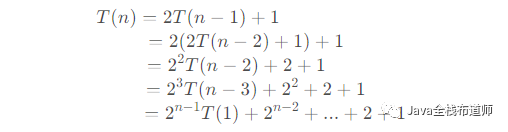
又因當n=1時，T(1)=1，得：

解得n階漢諾塔移動次數為： 次。

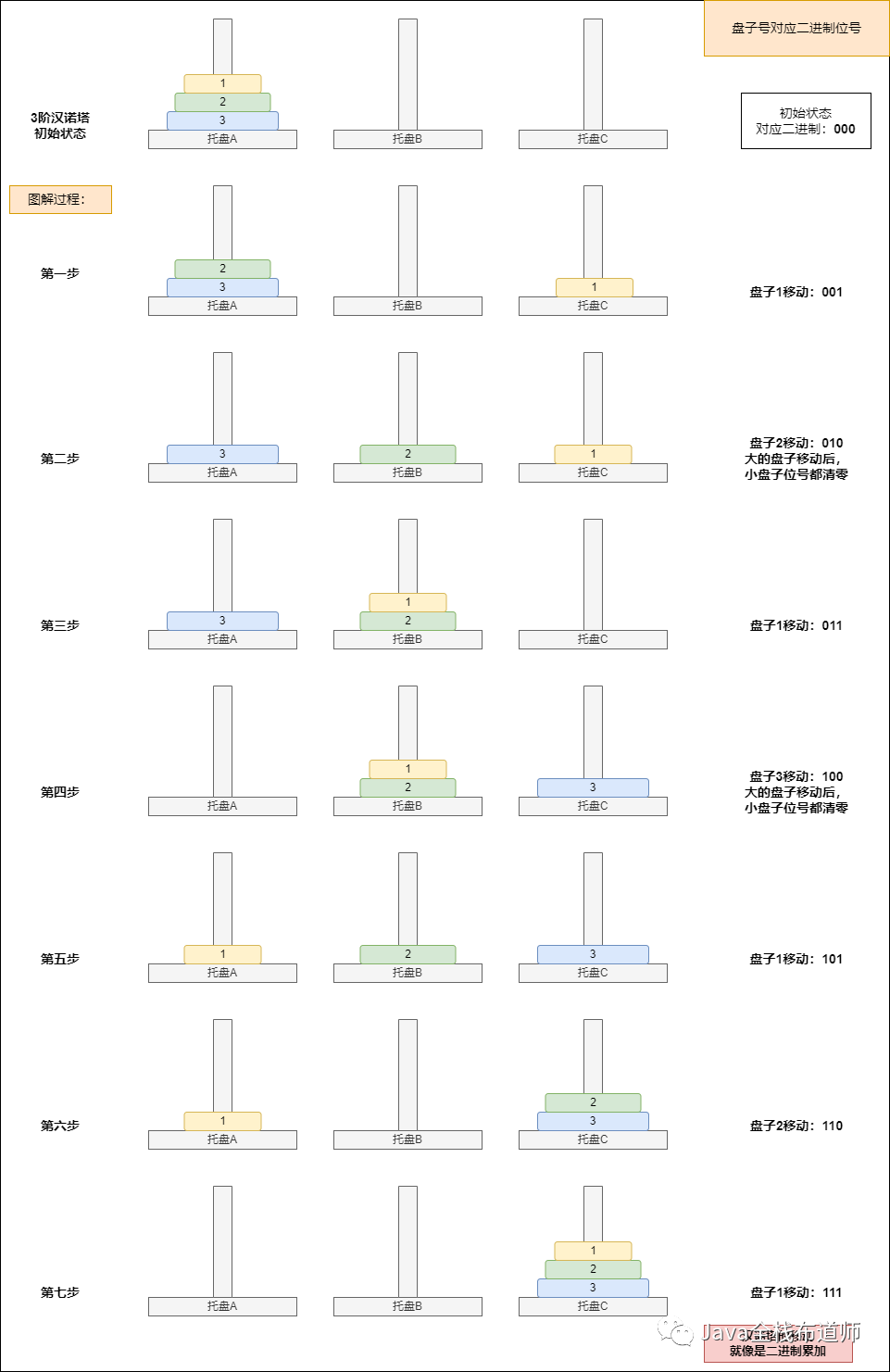
漢諾塔與二進位制

公式

這就像是n位二進位制的和，最終得到n位二進位制的最大值（全1）

所以有，n階漢諾塔移動次數等於n位二進位制得最大值，如：4階漢諾塔移動次數為

每個盤子的移動次數，觀察下圖：

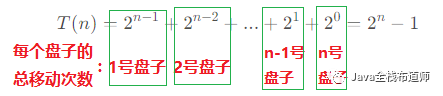
如圖可知，每個盤子移動總次數剛好相反，

所以，n階漢諾塔的第i個盤子總的移動次數為：

3階漢諾塔圖解與二進位制關係

漢諾塔與滿二元樹

遞迴演演算法會有相對應的遞迴樹，而漢諾塔的遞迴樹剛好是滿二元樹，即所有分支結點都有兩個葉子結點。

調整漢諾塔對演演算法程式碼的輸出資訊後：

public class Hanoi {
    // 階數
    private static int n = 3;
    public static void main(String[] args) {
        System.out.println(String.format("%s層漢諾塔的移動順序：", n));
        int sum = moveTree(n, 'A','B','C');
        System.out.println("漢諾塔移動次數："+sum);
    }

    /**
     * 漢諾塔與滿二元樹
     * (n-1) A -> B
     *   n   A -> C
     * (n-1) B -> C
     * 
     * 結束條件為：當n=1 時， A -> C
     */
    public static int moveTree(int n,char A, char B, char C) {
        if(n==1)
            System.out.println(String.format("第 %s 層(葉子節點)：%s -> %s",n, A, C));
        else {
            moveTree(n-1, A, C, B);//每次都是輸出A->C，所以要看到A->B，就需要將B和C交換

            if(n==Hanoi.n)
                System.out.println(String.format("第 %s 層(根節點)：%s -> %s", n, A, C));
            else
                System.out.println(String.format("第 %s 層(分支結點)：%s -> %s", n, A, C));

            moveTree(n-1, B, A, C);//每次都是輸出A->C，所以要看到B->C，就需要將A和B交換
        }
        //漢諾塔的移動次數為: 2^n-1
        return (int) Math.pow(2, n)-1;
    }

}

3層漢諾塔的移動順序：

第 1 層(葉子節點)：A -> C

第 2 層(分支結點)：A -> B

第 1 層(葉子節點)：C -> B

第 3 層(根節點)：A -> C

第 1 層(葉子節點)：B -> A

第 2 層(分支結點)：B -> C

第 1 層(葉子節點)：A -> C

漢諾塔移動次數：7

3階漢諾塔對應的滿二元樹：

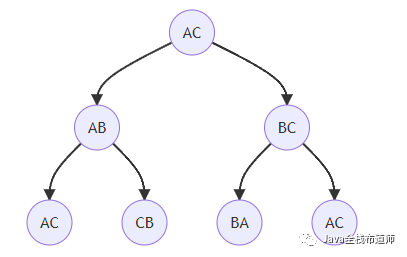
3階漢諾塔的移動步驟為滿二元樹的中序遍歷：AC、AB、CB、AC、BA、BC、AC

從輸出結果可以看到，漢諾塔盤子編號對應滿二元樹自底向上計算的層號，如：1號盤子的移動對應是葉子節點，最底層盤子對應根節點。

為了更好理解，可以寫成這樣：

    public static int moveTree(int n,char A, char B, char C) {
        if(n==1)
            System.out.println(String.format("第 %s 層(葉子節點)：%s -> %s",Hanoi.n-n+1, A, C));
        else {
            moveTree(n-1, A, C, B);//每次都是輸出A->C，所以要看到A->B，就需要將B和C交換

            if(n==Hanoi.n)
                System.out.println(String.format("第 %s 層(根節點)：%s -> %s", Hanoi.n-n+1, A, C));
            else
                System.out.println(String.format("第 %s 層(根節點)：%s -> %s", Hanoi.n-n+1, A, C));

            moveTree(n-1, B, A, C);//每次都是輸出A->C，所以要看到B->C，就需要將A和B交換
        }
        //漢諾塔的移動次數為: 2^n-1
        return (int) Math.pow(2, n)-1;
    }

漢諾塔遞迴實現與二元樹中序遍歷的遞迴實現，在程式碼實現上很類似

public static void inorder(TreeNode root) {
    if (root == null)
        return;
    inorder(root.left);
    System.out.print(root.val);
    inorder(root.right);
}

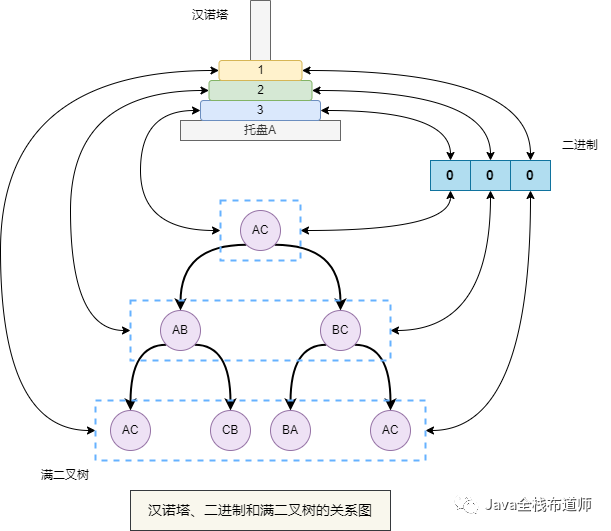
漢諾塔的移動步驟可以用滿二元樹的中序遍歷來表示，反過來，我們可以通過滿二元樹的特性推匯出漢諾塔的一些特性：

• 滿二元樹總的結點數為，所以漢諾塔移動次數為；

• 滿二元樹第n層的節點數為，所以n階漢諾塔第i個盤子被移動的次數為；

• 滿二元樹葉子節點數為,所以漢諾塔第一個盤子被移動的次數為；

• 滿二元樹是二進位制的一種表現形式，所以漢諾塔也是二進位制的一種表現形式，其中漢諾塔的移動過程就是二進位制的累加過程。

最後附上三者的關係圖

總結

如果這些結論都是自己推導發現的話，你會發現充滿驚喜。其推導過程非常有意思，好像冥冥之中萬物都和二進位制相關。文章想表達的不僅僅是得出漢諾塔有哪些特性，更重要的是希望能在學習中，發現學習本身的樂趣，從而滋養內在的好奇心、探索精神，不斷地自我推進，讓學習越來越有趣越有動力。